Impact of lubricant traction coefficient on cage’s dynamic characteristics in high-speed angular contact ball bearing

Zhng Wenhu,Deng Sier,Chen Guoding,Cui Yongcun

aSchool of Mechatronics Engineering,Northwestern Polytechnical University,Xi’an 710071,China

bSchool of Mechatronics Engineering,Henan University of Science and Technology,Luoyang 471003,China

cCollaborative Innovation Center of Major Machine Manufacturing in Liaoning,Dalian 116024,China

Impact of lubricant traction coefficient on cage’s dynamic characteristics in high-speed angular contact ball bearing

Zhang Wenhua,Deng Sierb,c,*,Chen Guodinga,Cui Yongcuna

aSchool of Mechatronics Engineering,Northwestern Polytechnical University,Xi’an 710071,China

bSchool of Mechatronics Engineering,Henan University of Science and Technology,Luoyang 471003,China

cCollaborative Innovation Center of Major Machine Manufacturing in Liaoning,Dalian 116024,China

Dynamic characteristic;High-speed angular contact ball bearing;Lubricant traction coefficient;Poincare´map;Stability

In this paper,the formulas of elasto-hydrodynamic traction coefficients of three Chinese aviation lubricating oils,4109,4106 and 4050,were obtained by a great number of elastohydrodynamic traction tests.The nonlinear dynamics differential equations of high-speed angular contact ball bearing were built on the basis of dynamic theory of rolling bearings and solved by Gear Stiff(GSTIFF)integer algorithm with variable step.The impact of lubricant traction coeff icient on cage’s dynamic characteristics in high-speed angular contact ball bearing was investigated,and Poincare´map was used to analyze the impact of three types of aviation lubricating oils on the dynamic response of cage’s mass center.And then,the period of dynamic response of cage’s mass center and the slip ratio of cage were used to assess the stability of cage under various working conditions.The results of this paper provide the theoretical basis for the selection and application of aviation lubricating oil.

1.Introduction

As one of basis parameters for dynamic design of rolling bearing,lubricant traction coefficient is affected by the combined impacts of slip velocity,rolling velocity and contact stress between roller and raceway,the temperature of lubricating oil,etc.Any changes in the above-mentioned factors might revise the traction behavior of lubricant between roller and raceway,causing the changes of collision force and collision frequency between cage and ball,which directly affect the stability of cage.Three types of Chinese aviation lubricating oils,namely 4109,4106 and 4050,are commonly used for lubrica-tion of angular contact ball bearing for high-speed spindle under various working conditions.However,owing to the different physics,chemistry and mechanics properties of lubricants,the systematic researchesin the connectionsof lubricant traction coefficient and cage’s dynamic characteristics are quite rare.

In 1971,Walters1firstly built the analytic model of highspeed ball bearing,which set the foundation of dynamic analysis of high-speed ball bearing.Gupta2–5built the dynamics differential equations of ball bearing with six degrees of freedom,and then studied the cage’s whirl orbit.By stimulating,Gupta P K indicated that the frictional coefficient between ball and raceway had great impact on cage’s whirl orbit,but he did not further study the influencing factors of cage’s stability.Further to previous research,Gupta6studied the relationship between structural parameters of cage pocket clearance,guide clearance and cage stability,but neglecting the impact of lubricant properties on the stability of cage.Based on the simplified traction model of lubricant,Boesiger et al.7studied the impact of operation conditions on cage’s whirl orbit and unsteady characteristic frequency in ball bearing,pointing out that oil lubrication was more preferable than grease lubrication in terms of cage stability.Lord and Larsson8did the experimental studies of elasto-hydrodynamic traction properties for VG46,VG68 and VG150,analyzing the impact of lubricant properties on lubricant film and traction coefficient,but their research did not involve the impact of lubricant properties on cage’s stability.Rahman and Ohno9did the experiments of the fatigue life and impact performance of bearings,which were lubricated by eight types of synthesized lubricants,analyzing the lubrication film between cage and ball and the reasons for cage’s failure.In addition,in their research,they indicated that lubricant traction coefficient had great impact on cage’s failure.Based on the quasi-dynamic theory of angular contact ball bearing,Deng and Hao10studied the effect of different working conditions and structural parameters on the offset of cage’s mass center,which had been used to assess cage’s stability.Pederson et al.11developed a flexible cage model with six degrees of freedom in deep groove ball bearing,and studied cage’s instability and ball-to-cage pocket contact forces.Based on dynamic theory of angular contact ball bearing,Liu and Deng12studied the effect of working conditions and structural parameters on cage’s whirl orbit and the speed deviation ratio of cage,which were used to assess the cage’s stability.Based on dynamic theory of rolling bearing,Deng and Xie13studied the dynamic characteristics of cage in high-speed angular contact ball bearing,pointing out that too big or too small pocket clearance and the guiding clearance of cage were adverse to cage’s stability.Sathyan et al.14conducted various tests such as run-in test,temperature test,and over-lubrication test to study the instability of cage in ball bearings,and the study results show that square pocket retainers are more stable compared to circular pocket retainers.Ashtekar and Sadeghi15developed a 3D explicit finite element model(EFEM)of the cage to analyze the cage dynamics,deformation,and resulting stresses in a ball bearing under various operating conditions.Ye16studied the effect of cage clearance ratio,bearing load and bearing rotation speed on cage’s whirl orbit and the speed deviation ratio of cage,suggesting that too big or too small pocket clearance and guiding clearance of cage were not beneficial to cage’s stability.Abele et al.17promoted two new image evaluation algorithms to capture cage’s whirl with sensors installed on a bearing test rig,and analyzed the cage motion in an angular contact ball bearing under the operation conditions.All the above mentioned researches mainly focused on the impact of bearing working conditions and structural parameters on cage’s dynamic characteristics and stability,while the impact of lubricant traction coefficient on cage’s dynamic characteristics and stability has not aroused any attention.

In this paper,the formulas of elasto-hydrodynamic traction coefficients of three Chinese aviation lubricating oils,4109,4106 and 4050,are obtained through a great number of elasto-hydrodynamic traction tests.The nonlinear dynamics differential equations are built on the basis of dynamic theory of rolling bearings and solved by Gear Stiff(GSTIFF)integer algorithm with variable step.The impact of lubricant traction coefficient on cage’s dynamic characteristics is investigated,and Poincare´map is used to analyze the impact of three types of aviation lubricating oils on dynamic response of cage’s mass center and the slip ratio of cage.The period of dynamic response of cage’s mass center and the slip ratio of cage are used to assess cage’s stability and the research results of this paper provide theoretical basis for the selection of aviation lubricating oil.

2.Elasto-hydrodynamic traction coefficient tests

The tests of elasto-hydrodynamic traction coefficients for three Chinese aviation lubricating oils,4109,4106 and 4050,were conducted by using a self-made test rig.The construction of test rig is shown in Fig.1,where B direction denotes the left view of local type view.

According to the dynamic viscosity and temperatureviscosity coefficient,the three Chinese aviation lubricating oils,4109,4106 and 4050,are categorized to the low viscosity lubricant,medium viscosity lubricant,and medium viscosity,hightemperature resistant lubricant,respectively.

The formulas of elasto-hydrodynamic traction coef ficients l of 4109,4106 and 4050 were obtained by applying the curve fitting technic to the test data.

Fig.1 Construction of test rig.

Table 1 Parameters of aviation lubricating oil.

In Eq.(1),Sis slide-roll ratio of ball;AL,BL,CL,DLare functions of normal load,lubrication temperature of inlet and velocity of contact surface,and the expressions ofAL,BL,CL,DLfor 4109,4106 and 4050 are shown as Eqs.(2)–(4),respectively.

3.Dynamic model of high-speed angular contact ball bearing

In this paper,outer ring is fixed,inner ring rotates at constant speed,and cage is guided by outer ring.The surfaces of bearing components are absolutely smooth,and the component’s mass center coincides with its centroid.In order to build the dynamic model of bearing,the following five coordinate systems in Fig.2 are defined.

(1)Inertial coordinate system{O;X,Y,Z}is fixed in space,Xaxis coincides with rotating axis of bearing,andYZplane parallels to radial plane through bearing center.

(2)Coordinate system of ball mass center{obj;xbj,ybj,zbj},where subscriptjdenotes thejth ball or cage pocket.objcoincides with ball’s mass center,ybjaxis is along radial direction of bearing,andzbjaxis is along circumferential direction of bearing.{obj;xbj,ybj,zbj}moves but doesn’t spin with ball’s mass center,and each ball has its own local coordinate system.

(3)Coordinate system of cage’s mass center{oc;xc,yc,zc}.xcaxis coincides with rotating axis of cage,yczcplane parallels to radial plane through cage center,occoincides with geometric center of cage,and{oc;xc,yc,zc}moves and spins with cage.

(4)Coordinate system of inner ring mass center{oi;xi,yi,zi}.xiaxis is along with rotating axis of inner ring,yiziplane parallels with radial plane through inner ring mass center,oicoincides with geometric center of inner ring,and{oi;xi,yi,zi}moves and spins with inner ring.

(5)Coordinate system of thejth cage pocket center{opj;xpj,ypj,zpj}.opjcoincides with geometric center of cage pocket,ypjaxis is along radial direction of bearing,andzpjaxis is along circumferential direction of bearing.{opj;xpj,ypj,zpj}moves and spins with cage,and each cage pocket center has its own local coordinate system.

3.1.Nonlinear dynamics differential equations of ball

When angular contact ball bearing is working at high speed,the forces acting on ball are shown in Fig.3.For the detailed expressions of symbols,please refer to Ref.18.

Fig.2 Coordinate system of ball bearing.

The nonlinear dynamics differential equations of thejth ball are shown as Eqs.(5)–(10):

Fig.3 Schematic diagram of forces acting on ball.

3.2.Nonlinear dynamics differential equations of cage

The forces acting on cage are shown in Fig.4,and{or;yr,,zr}is cage’s reference coordinate system.For the expressions of symbols in Fig.4,please refer to Ref.18.

The nonlinear dynamics differential equations of cage are shown as Eqs.(11)–(16):

Fig.4 Schematic diagram of forces acting on cage.

3.3.Nonlinear dynamics differential equations of inner ring

The nonlinear dynamics differential equations of inner ring are shown as Eqs.(17)–(21):

4.Impact of lubricant traction coefficient on cage’s dynamic characteristics

The major parameters of high-speed angular contact ball bearing are shown in Table 2.

Due to the strong nonlinearity of dynamics differential equations of high-speed angular contact ball bearing,the solution of nonlinear equations is more complicated.Here,the nonlinear dynamics differential Eqs.(5)–(21)were solved by GSTIFF integer algorithm with variable step19,and Poincare´map20was used to analyze the whirl orbit of cage.

4.1.Impact analysis of lubricant temperature on dynamic response of cage’s mass center

Table 2 Major parameters of bearing.

Fig.5 Whirl orbit and Poincare´map under different temperatures of 4109.

As shown in Fig.5,with the temperature of 4109 increasing,the whirl orbit of cage presents the single circle whirl,the less obvious multi-circle whirl and the obvious multicircle whirl.One Poincare´mapping point,three Poincare´mapping points and the closed curve formed by Poincare´mapping points in Fig.5(a)–(c)indicate that cage undergoes one period,three periods and quasi-periodicity at different lubricant temperatures,respectively.

In Fig.6,both the temperatures of 4106 and 4050 have tiny impact on the dynamic response of cage,and cage keeps whirling along one circle and less obvious multiple circles,respectively.The Poincare´points in Fig.6(a)and(b)also show that cage is in the state of one periodic motion and four periodic motion respectively,no matter how the temperature of 4106 and 4050 changes.

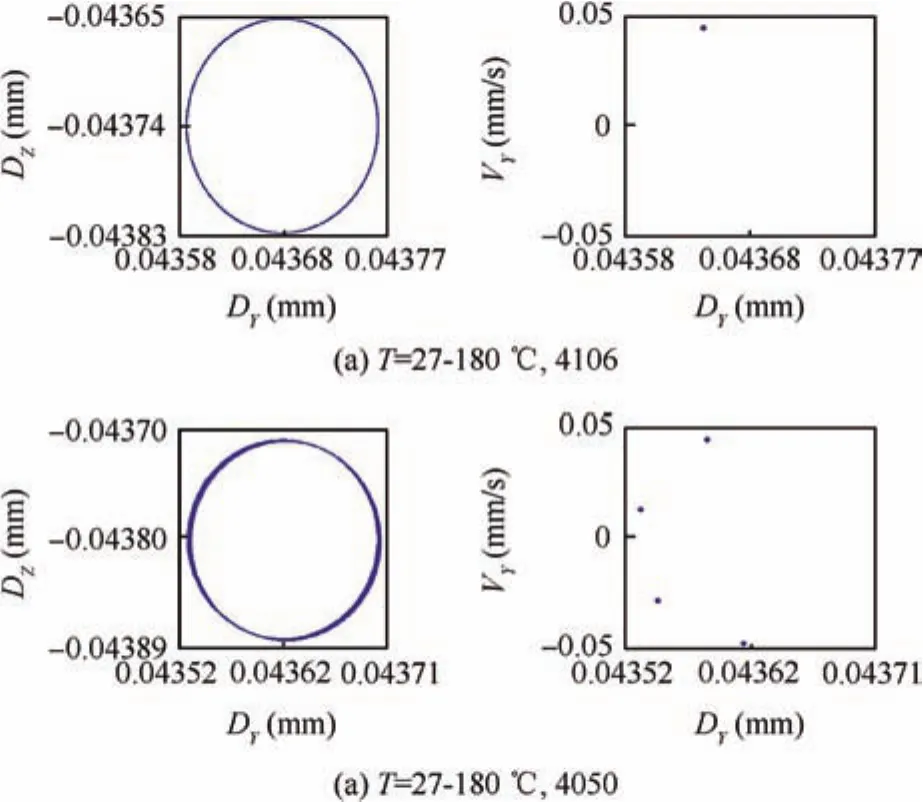
Fig.6 Whirl orbit and Poincare´map under different temperatures of 4106 and 4050.

Fig.7 Whirl orbit and Poincare´map under different axial forces of 4109.

4.2.Impact analysis of axial force on dynamic response of cage’s mass center

We assume that the speed of inner ring is set to 14,000 r/min,axial forceFxapplied on inner ring are set to 100 N,500 N,1000 N,2000 N,3000 N and 6000 N,and lubricant temperatureTis set to 130℃.

In Fig.7,bearing is lubricated by 4109,and when axial load is small(Fx=100 N),the whirl orbit of cage and Poincare´mapping points in Fig.7(a)are disorderly,indicating that cage is in the chaotic state.With axial load increasing(Fx=500–2000 N),cage successively undergoes the single circle whirl and the multi-circle whirl.Four Poincare´mapping points in Fig.7(b)and the closed curve formed by Poincare´mapping points in Fig.7(c)show that cage is in the four periodic and quasi-periodic state,respectively.When axial loadFxis in the range of 3000–6000 N,the disorderly Poincare´mapping points in Fig.7(d)show that cage is in chaotic state.

In Fig.8,bearing is lubricated by 4106,and when axial load is small(Fx=100 N),the disorderly whirl orbit of cage and Poincare´mapping points in Fig.8(a)show that cage is in a chaotic state.With axial load increasing(Fx=500–3000 N),both the single circle whirl of cage and one Poincare´mapping point in Fig.8(b)represent that cage is in the state of single period.When axial loadFxis up to 6000 N,the less obvious multi-circle whirl of cage and the closed curve formed by Poincare´mapping points in Fig.8(c)also represent that cage is in a quasi-periodic state.

Fig.8 Whirl orbit and Poincare´map under different axial forces of 4106.

In Fig.9,bearing is lubricated by 4050,and when axial load is small(Fx=100 N),the disorderly whirl of cage and Poincare´mapping points in Fig.9(a)represent that cage is in the state of chaotic motion.When axial loadFxis up to 500 N,both the single circle whirl of cage and one Poincare´mapping point in Fig.9(b)show that the motion of cage’s mass center is in the state of single period.With axial load increasing(Fx=1000–2000 N),four Poincare´mapping points in Fig.9(c)represent that cage is in the state of four periodic motion.When axial load is big enough(Fx=3000–6000 N),as shown in Fig.9(d)and(e),cage undergoes the quasi-periodic motion and the chaotic motion,respectively.

Fig.9 Whirl orbit and Poincare´map under different axial forces of 4050.

Fig.10 Whirl orbit and Poincare´map under different radial forces of 4109.

4.3.Impact analysis of combined loads on dynamic response of cage’s mass center

We assume that the speed of inner ring is set to 14,000 r/min,radial forcesFyapplied on inner ring are set to 100 N,500 N and 1000 N,axial forceFxapplied on inner ring is set to 1000 N,and lubricant temperatureTis set to 130℃.

In Fig.10,when bearing is lubricated by 4109,the multicircle whirl of cage is less obvious,and the closed curve formed by Poincare´mapping points also represents that cage is in the state of quasi-periodic motion,no matter how radial forceFychanges.

In Fig.11,bearing is lubricated by 4106.When radial load is small,cage undergoes a single circle whirl,and one Poincare´mapping point in Fig.11(a)shows that cage is in the state of one periodic motion.With radial load increasing,the multicircle whirl increases obviously,and closed curve in Fig.11(b)and disorderly Poincare´mapping points in Fig.11(c)also show that cage undergoes quasi-periodic motion and ultimately tends to chaotic motion.

In Fig.12,when bearing is lubricated by 4050,Poincare´mapping points in Fig.12(a)and(b)indicate that cage undergoes four periodic and chaotic motion with the increase of the radial load,respectively.

Fig.11 Whirl orbit and Poincare´map under different radial forces of 4106.

Fig.12 Whirl orbit and Poincare´map under different radial forces of 4050.

Fig.13 Cage slip ratio under different lubricant temperatures.

Fig. 14 Cage slip ratio under different axial forces(Speed=14000 r/min,T=130℃).

5.Impact analysis of lubricant traction coefficient on cage’s stability

According to the above analysis in Section 4,the motion of cage in angular contact ball bearing lubricated by 4109,4106 and 4050 shows the different dynamic responses and changing pattern under various working conditions.However,it is inadequate to assess the stability of cage with just a dynamic response result.

In this paper,the slip ratio of cage and the period of dynamic response of cage’s mass center were used as the criteria to assess the stability of cage.The cage’s slip ratio and the period of nonlinear dynamic response of cage’s mass center under different lubricant temperatures,axial loads and radial loads are shown in Figs.13–15 and Tables 3–5.

In Figs.13–15,cage’s slip ratio shows the different changing trends under different lubricant temperatures and axial forces.But,radial force has tiny impact on cage’s slip ratio when bearing bears combined loads.

Fig.15 Cage slip ratio with different radial forces(Fx=1000 N,Speed=14000 r/min,T=130℃).

Table 3 Nonlinear dynamic response period of cage at different lubricant temperatures.

Table 4 Nonlinear dynamic response period of cage at different axial forces.

According to the above-mentioned analysis,it is apparent that different types of lubricating oils have great impact on cage’s dynamic characteristics and the stability of cage.Fewer periods of dynamic response of cage’s mass center and smaller slip ratio of cage are beneficial to cage’s stability.Therefore,in order to improve the stability of cage,the type of aviation lubricating oil is chosen according to Table 6 under different working conditions.

Table 5 Nonlinear dynamic response period of cage at different radial forces.

Table 6 Recommended working condition for three aviation lubricating oils.

6.Conclusions

(1)Lubricant traction coefficient affects the dynamic characteristics of cage,and the motion of cage’s mass center shows the abundant periodic and non-periodic(quasiperiodic and chaotic)responses.In addition,cage’s whirl orbit presents different periods of nonlinear response and changing pattern in angular contact ball bearings lubricated by different types of aviation lubricating oils.

(2)For three types of aviation lubricating oils,4109,4106 and 4050 in this paper,a too small or too large axial force is adverse to cage’s stability.With the increase of axial force,cage might undergo from chaotic state to periodic motion,and then ultimately tend to quasiperiodic state or chaotic state.

(3)When bearing only bears an axial force,for the sake of cage’s stability,lubricant with low viscosity is suggested for lubrication of bearing working at high speed,light load and low temperature;lubricant with medium viscosity is suggested for lubrication of bearing working at high speed,heavy load and low temperature;lubricant with the medium and high temperature resistant is suggested for lubrication of bearing working at high speed,heavy load and high temperature.

(4)When bearing simultaneously bears an axial force and a

radial force,for the sake of cage’s stability,lubricant with medium viscosity and high temperature resistant is suggested for lubrication of bearing working at high speed,high temperature and heavy radial load;lubricant with low viscosity is suggested for lubricating of bearing working under any other working condition.

Acknowledgements

The study was financially co-supported by the National Natural Science Foundation of China(No.U1404514),Henan Outstanding Person Foundation(No.144200510020)of China and Collaborative Innovation Center of Major Machine Manufacturing in Liaoning,China.

1.Walters CT.The dynamics of ball bearings.J Lubr Tech1970;93(1):1–10.

2.Gupta PK.Dynamics of rolling element bearings.Parts I,II,III and IV.J Lubr Tech1979;101(3):293–326.

3.Gupta PK.Some dynamic effects in high-speed solid-lubricated ball bearings.Tribol Trans1983;26(3):393–400.

4.Gupta PK.Advanceddynamicsofrollingelements.New York:Springer Verlag;1984.p.76–99.

5.Gupta PK.Frictional instabilities in ball bearings.Tribol Trans1988;31(2):258–68.

6.Gupta PK.Modeling of instabilities induced by cage clearances in ball bearings.Tribol Trans1991;34(1):93–9.

7.Boesiger EA,Donley AD,Loewenthal S.An analytical and experimental investigation of ball bearing retainer instabilities.Analyst1992;114(3):530–9.

8.Lord J,Larsson R.Effects of slide-roll ratio and lubricant properties on elastohydrodynamic lubrication film thickness and traction.Proc Inst Mech Eng2001;215:301–8.

9.Rahman MZ,Ohno N.Effect of lubricating oils on cage failure of ball bearings.Tribol Trans2003;46(4):499–505.

10.Deng SE,Hao JJ.Dynamics analysis on cage of angular contact ball bearings.Bearing2007;10:1–5[Chinese].

11.Pederson BM,Sadeghi F,Wassgren C.The effects of cage flexibility on ball-to-cage pocket contact forces and cage instability in deep groove ball bearings.SAE Tech Pap2006;1:0358–372.

12.Liu XH,Deng SE.Dynamic stability analysis of cages in highspeed oil-lubricated angular contact ball bearings.Trans Tianjin Univ2011;17:20–7.

13.Deng SE,Xie PF.Flexible-body dynamics analysis on cage of high-speed angular contact ball bearing.Acta Armamentarii2011;32(5):293–311.

14.Sathyan K,Gopinath K,Lee SH,Hsu HY.Bearing retainer designs and retainer instability failures in spacecraft moving mechanical systems.Tribol Trans2012;55(4):503–11.

15.Ashtekar A,Sadeghi F.A new approach for including cage flexibility in dynamic bearing models by using combined explicit if nite and discrete element methods.J Tribol2012;134(4):041502.

16.Ye ZH.Cage instabilities in high-speed ball bearings.Appl MechMater2013;278–280:3–6.

17.Abele E,Holland L,Nehrbass A.Image acquisition and image processing algorithms for movement analysis of bearing cages.J Tribol2015;138(2):021105.

18.Deng SE,Jia QY,Xue JX.Design principle of rolling bearings.2rd ed.Beijing:China Standard Press;2014.p.225–37[Chinese].

19.Gear CW.Simultaneous numerical solution of differential-algebraic equations.IEEE Trans Circ Theor1971;18(1):89–95.

20.Harsha SP,Sandeep K,Prakash R.The effect of speed of balanced rotor on nonlinear vibrations associated with ball bearings.Int J Mech Sci2003;45(4):725–40.

8 March 2016;revised 5 April 2016;accepted 10 May 2016

Available online 15 October 2016

*Corresponding author at:School of Mechatronics Engineering,Henan University of Science and Technology,Luoyang 471003,China.Tel.:+86 379 64270625.

E-mail addresses:526916105@qq.com(W.Zhang),dse@haust.edu.cn(S.Deng),gdchen@nwpu.edu.cn(G.Chen),372865368@qq.com(Y.Cui).

Peer review under responsibility of Editorial Committee of CJA.