超声速非平衡电离磁流体流动控制试验和数值模拟

李益文， 樊昊， 张百灵， 王宇天， 段成铎， 高岭， 庄重， 何国强

1.西北工业大学 航天学院 燃烧、流动和热结构重点实验室， 西安 710072 2.空军工程大学 等离子体动力学实验室， 西安 710038

超声速非平衡电离磁流体流动控制试验和数值模拟

李益文1,2,*， 樊昊2， 张百灵2， 王宇天2， 段成铎2， 高岭2， 庄重2， 何国强1

1.西北工业大学 航天学院 燃烧、流动和热结构重点实验室， 西安 710072 2.空军工程大学 等离子体动力学实验室， 西安 710038

为了开展磁流体(MHD)流动控制原理研究，建立了磁流体技术试验系统，采用电容耦合射频-直流组合放电对Ma=3.5 气流进行电离，在磁场作用下产生顺/逆气流方向的洛伦兹力控制流场，采用试验段静压变化来监测磁流体流动控制效果，通过一维模型计算磁流体流动控制过程中流场变化情况，分析磁流体流动控制效果；通过添加电磁源项的Navier-Stokes方程耦合电势泊松方程建立了二维磁流体动力模型，对磁流体流动控制进行数值模拟研究。主要结论如下：在磁场约束下，电容耦合射频-直流组合放电能够在Ma=3.5流场中产生大体积均匀电流，电导率约0.015 S/m；在焦耳热和洛伦兹力作用下，磁流体加速时静压升高了130 Pa，减速时静压升高了200 Pa；磁流体流动控制过程中，仅有不足10%的能量在磁流体通道内发生了作用；数值模拟结果显示，在试验条件下，加速时静压升高了128 Pa，减速时静压升高了208 Pa，与试验结果基本吻合。

等离子体； 磁流体流动控制； 超声速； 非平衡电离； 电导率

超燃冲压发动机在非设计马赫数下工作时会出现推力下降和外部阻力增大等问题，严重时甚至引起进气道不起动、发动机喘振和熄火[1-3]。为了使超燃冲压发动机能够在更宽的马赫数范围内保持良好的推进性能，在非设计工况下需要对其进气道流场进行调控。磁流体流动控制作为一种主动控制手段，在超燃冲压发动机进气道流场控制方面具有良好的应用前景[4-8]。

磁流体流动控制基本原理是通过空间内的导电流体与外部磁场相互作用，产生顺/逆气流方向的洛伦兹体积力(以下简称洛伦兹力)，对流场进行加/减速，改变流场气动特性，实现对流场的整体控制。相比于传统的变几何控制方式，具有响应迅速、无复杂机械结构、不存在热防护和密封等特点，可能实现固定几何进气道宽范围调控，带来良好的推进效益。

俄罗斯学者Bobashev等[9-11]基于激波管开展了平衡电离磁流体流动控制试验研究，采用稀有气体氙作为工质气体，试验段流场速度为2 100 m/s，气体平衡电离产生的等离子体电导率达600 S/m。在磁感应强度B=-1.3 T时，对比顺/逆气流方向洛伦兹力作用下斜激波的激波角发现，洛伦兹力的作用改变了入口气流的马赫数，同时由于霍尔效应的影响，上下流场不对称分布。

尽管Bobashev等进行的试验已经在原理上证明了磁流体流动控制的可行性，但是无法应用于真实飞行环境中的冲压发动机进气道流动控制，因为Bobashev等采用的平衡电离需要气体温度很高(T*>3 000 K)才能实现。对于高超声速进气道，当飞行马赫数达到12以上才有可能出现平衡电离，即使加碱金属电离种子也需要飞行马赫数达到8以上才能出现平衡电离等离子体[12]。因此针对冲压发动机进气道的磁流体流动控制研究应采用非平衡电离产生等离子体。

美国俄亥俄州立大学Nishihara等[13-15]针对非平衡电离磁流体流动控制开展了试验与数值模拟研究，采用纳秒脉冲-直流组合放电的方式产生并维持大体积电流，在马赫数4的超声速流场中，加速洛伦兹力的作用使试验段静压上升了11%，减速洛伦兹力的作用使静压上升了19%。同时采用三维磁流体动力学模型开展数值模拟对比研究，计算结果与试验吻合度很高，加速和减速洛伦兹力作用时静压分别上升了8%和18%，而加速洛伦兹力作用时气流速度基本不变；减速洛伦兹力作用时，气流速度降低了15 m/s。但是由于纳秒脉冲放电自身放电方式的限制，在单个放电周期内，通道内的等离子体和大体积电流衰减严重，制约了磁流体流动控制的效果。

本文针对纳秒脉冲放电不连续的缺点，采用电容耦合射频-直流组合放电的形式对Ma=3.5气流进行预电离并产生大体积均匀电流，开展磁流体流动控制试验研究，并采用二维磁流体动力模型对影响流动控制效果的因素进行分析。

1 试验系统

试验系统主要由小型吸气式超声速风洞、电容耦合射频放电电路、直流放电回路、电磁铁以及数据采集系统组成，如图1所示。

小型吸气式超声速风洞采用二元型面，设计马赫数3.5，材料采用有机玻璃，主要由收缩段、扩张段、试验段以及扩压段组成。风洞上游通过连接真空减压阀和过滤器调节进口状态，下游连接真空舱来提供低气压环境。风洞的试验段又称磁流体通道，截面积为10 mm×20 mm。打开阀门，超声速喷管启动，在进口总压为3.5×104Pa、真空舱压力为300 Pa时，风洞稳定运行时间为15 s 左右，稳定运行时试验段静压约为500 Pa，气流马赫数3.44，气流速度为651 m/s，静温为90 K，风洞的质量流量为2.6 g/s。

在磁流体通道左右两边镶嵌电容耦合射频放电电极，并覆盖陶瓷板绝缘介质，面积大小为 40 mm×40 mm，放电电源为AG1017L型射频电源，输出功率0～200 W，在射频电路中串联电感线圈达到阻抗匹配。典型条件下，超声速流场中电容耦合射频放电波形如图2所示，波形为正弦波，波形稳定无明显畸变，说明放电稳定，同时也说明试验段超声速气流比较稳定。

直流放电回路与射频放电回路正交布置，主要作用在于产生并维持大体积电流，并且串联了电感线圈来抑制电流波动。为了防止射频放电电路对直流放电的干扰，在直流电路中串联2个30 kV/2 A 的硅堆。磁场由电磁铁产生，在直径80 mm的磁极范围内，能够产生0～1.7 T的均匀横向磁场。磁场的作用可以大大增强超声速气流中放电的均匀性，如图3所示。

数据采集系统主要包括电参数和流场参数的采集，电参数包括电容耦合射频放电和直流放电的电压电流，主要通过P6015A高压探针和TCPA300+TCP312电流探针进行采集并采用DPO4104示波器保存数据。

由于磁流体通道的内部空间比较小，直接测量流场马赫数会对流场产生很大影响，因此试验中采用绝压变送器测量流场静压的变化来反映流场特性。由于外部强磁场和高频放电带来的强电磁干扰，绝压变送器在磁流体通道附近无法正常工作，试验中在磁流体通道下游10 mm处开静压孔，通道橡胶管将压力导出，将绝压变送器放置在屏蔽箱中，保证绝压变送器能够正常工作。同时橡胶管必须具有一定的截面积，能够及时响应试验段压力信号，又不会影响流场质量。经过大量试验证明，屏蔽箱距离试验段2 m以外后电磁干扰对试验段压力信号的测量影响可以忽略，橡胶管内径为2 mm时压力信号响应比较迅速，测量时对流场的影响可以忽略不计，能够满足试验要求。

2 试验结果及分析

2.1 直流放电特性

大体积、均匀电流是开展磁流体流动控制的关键，由于超声速流场边界层和电容耦合射频放电本身的限制，放电等离子体没有充满整个磁流体通道，在上下壁面存在小范围的暗区。为了产生大体积均匀电流，需要高直流电压将暗区击穿。

图4为超声速条件下、电容耦合射频放电功率为35 W、无磁场作用时的直流放电波形，直流电压上升到800 V左右时，超声速流场中的暗区被击穿，回路出现电流。随后电压减小至500 V左右并维持不变，但是电流在放电过程中波动比较大，表明此时放电很不稳定，通道内可能出现电弧放电。

通过式(1)对空间放电等离子体的平均电导率进行计算

(1)

式中：l为上下壁面间距20 mm；S为磁流体通道中纵向电流的面积；U和I为直流放电的电压和电流，计算此时的电导率为0.2 S/m。从前期的诊断工作中可以得知，负载功率为35 W、频率为6.2 MHz的电容耦合射频放电产生的电导率约为0.015 S/m，远小于此时的电导率，判断此时通道内出现了电弧放电现象。根据电容耦合射频放电特性，电弧可能出现在左右壁面处，一般而言，电弧放电的电流能够达到101A量级，本试验中由于电感线圈和直流源本身的限流作用，放电电流不到2 A。由于磁流体流动控制是通过洛伦兹体积力发生作用的，因此应该避免放电电弧的产生，施加横向磁场正是抑制电弧的一种有效手段。

图5为超声速条件下、电容耦合射频放电功率35 W、B=1.7 T时的直流放电波形，在直流电压1 550 V时边界层暗区被击穿，平均电流约0.4 A，放电的电导率约为0.015 S/m；图6为超声速条件下、电容耦合射频放电功率35 W、B=-1.7 T时的直流放电波形，在直流电压1 450 V时边界层暗区被击穿，平均电流约0.5 A，放电的电导率约为0.02 S/m。从上述数据可以看到，施加横向磁场后，击穿电压升高，电导率减小，与诊断值基本一致，可以判断此时通道内的电弧被基本抑制，放电为大体积均匀放电，满足磁流体流动控制需求。

从图3的放电图像可以看到，施加磁场后等离子体在空间中的分布更加均匀，暗区会减小。但是直流放电的击穿电压却上升近一倍，说明磁场对纵向电流的形成具有很大的阻碍作用。从汤森放电理论可知，暗区的击穿过程就是电子在电场作用下加速碰撞电离的过程，但是磁场的作用约束了电子运动的轨迹。在电场强度较小时，阴极发射出来的电子甚至被约束在一定范围内，为了击穿暗区，形成纵向电流，必须采用更高的电场加速电子，从而“摆脱”磁场的约束作用。

产生加速洛伦兹力时，在磁场作用下注入的电能一部分转化为气体的动能，另一部分进行焦耳加热作用，增加分子势能；减速洛伦兹力作用时，在磁场作用下气体的一部分动能和注入的电能全部转化为分子势能，因此减速洛伦兹力作用下的气体分子更容易激发电离，平均电导率较高。

2.2 静压变化曲线

图7为加速洛伦兹力、减速洛伦兹力以及单独放电时的磁流体通道静压变化曲线，无磁场作用时，直流放电对压力曲线基本没有造成影响，主要是因为直流放电注入的电能先转化为分子振动能量，然后分子振动能量释放转化为焦耳热作用。但是由于磁流体通道长度仅仅为40 mm，而通道内气流的速度在650 m/s左右，因此气流经过通道时间为61 μs，注入的电能转化为分子振动能后在磁流体通道内来不及释放，导致直流放电在通道内的焦耳热作用有限，静压变化很小。

加速洛伦兹力时，试验段静压上升约130 Pa。从理论上讲，在气体流量不变的条件下，超声速气流速度增大将导致静压降低，而焦耳热作用则会导致速度降低、静压升高。加速洛伦兹力作用下静压的上升是加速效应和焦耳热共同作用的结果。改变磁场的方向产生减速洛伦兹力时，试验段的静压升高约200 Pa。

从图7中风洞的运行时间来看，减速洛伦兹力作用时风洞的运行时间明显缩短，这是由于在通道内施加了洛伦兹力作用的结果，洛伦兹力作用相当于在风洞运行时施加了一个扰动，导致风洞提前结束运行。从国外的研究文献来看[16-18]：加速洛伦兹力的作用能够减小气流附面层的密度波动，抑制附面层分离。因此加速洛伦兹力作用下，风洞的运行时间比减速洛伦兹力作用时要长。

2.3 准一维模型分析

试验中采用试验段静压变化来监测磁流体流动控制效果，静压的变化是由洛伦兹力和焦耳热共同作用。磁流体流动控制的主要目的是控制流场气流速度和马赫数，但是静压的变化无法直接反映磁流体流动控制后流场速度等参数的变化，因此需要通过静压的变化来计算流场其他参数的变化。根据磁流体流动控制过程中的动力学特性，建立沿气流方向的磁流体流动控制一维模型，通过一维模型计算磁流体流动控制过程中流场变化情况，分析磁流体流动控制效果。

结合通道中的实际情况及简化计算的需要，给出以下合理假设：

1) 磁流体通道横截面积不变，横截面上各个物理参数分布均匀。

2) 气流完全沿通道方向流动，不存在其他方向分量。

3) 温度、压力和速度是x的单值函数。

4) 不考虑气体的摩擦和热损耗。

5) 假定气体的定压比热和定容比热为常数。

基于以上的假设，磁流体流动控制一维模型如下

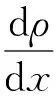
(2)

(3)

(4)

(5)

式中：u为气流速度；ρ为气体密度；T为温度；Bz为z方向磁感应强度；jy为y方向电流密度；q为磁流体通道内的能量源项；R为气体常数；Cp为定压比热。

试验中磁流体流动控制与外界之间的能量交换主要存在3个方面：

1) 直流源注入的电能。

2) 射频电源注入的能量。

3) 与外界之间的热交换。

首先，在试验中射频电源注入的负载功率为35 W，远小于直流源注入的能量，相比之下可以忽略。其次，尽管超声速气流的静温很低(T=90 K)，但由于超声速气流的边界层热效应，试验中超声速气流边界层处的温度非常接近室温，实际的热交换非常有限。因此注入气流中的能量采用直流源注入的电能，对直流放电电压电流曲线进行积分得到直流源注入能量，加速洛伦兹力时磁流体通道注入功率为560 W，减速洛伦兹力时功率为647 W。

从静压变化曲线分析可知，注入的电能转换成分子振动能后，大部分能量在磁流体通道内没来得及释放，因此作用在磁流体通道内的能量源项q为

(6)

式中：α为注入的电能在磁流体通道内发生作用的百分比；U和I为直流放电电压和电流，Ey为y方向电场强度。

联立一维方程式(2)～式(5)得

(7)

(8)

(9)

(10)

式中：Ma为马赫数；γ为绝热指数；p为压力。

上述方程中，马赫数Ma是关于气体状态参数u、T等的函数，因此上述方程为非线性方程，求解相对而言比较困难。由于磁流体通道内马赫数的变化较小，为了简化计算，合理地假设磁流体通道内的马赫数为定值，简化后的准一维方程为

(11)

(12)

(13)

式中：d为磁流体通道长度。从上述方程组可以看出，对流场参数发生作用的是焦耳热作用项和洛伦兹力作用项，引入磁流体通道的负载系数K来表征焦耳热作用与洛伦兹力作用的比例大小，K表征为

(14)

将试验中测量得到的电压、电流值以及压力变化值代入方程，进行磁流体加速流动控制时(下标A表示加速作用)，ΔpA=130 Pa，Bz=1.7 T，jy=1 050 A/m2，代入方程组式(11)～式(14)，计算得到αA=8.5%，KA=5.6，ΔuA=-4.8 m/s，试验段超声速气流速度降低至623 m/s，ΔT=23 K，静温上升至113 K。通过马赫数定义计算，此时的马赫数为2.93，马赫数降低了0.37。

进行磁流体减速流动控制时(下标R表示减速作用)，ΔpR=200 Pa，Bz=1.7 T，jy=1 250 A/m2，计算得到αR=7%，KR=4，ΔuR=-23.5 m/s，试验段超声速气流速度降低至604 m/s，ΔT=33 K，静温上升至123 K，通过马赫数定义计算，此时的马赫数为2.72，马赫数降低了0.58。

无论加速作用还是减速作用，直流放电注入超声速气流中的能量主要以分子振动能的形式储存，注入的电能在磁流体通道内发生作用的百分比α均小于10%，且分子振动能的释放受环境等因素影响，因此不同洛伦兹力作用时释放的能量比例略有不同，这与许多外国公开的文献资料相符[13,19-20]。

从流场参数看，超声速非平衡电离的磁流体流动控制效果不太理想，无论是磁流体加速作用还是减速作用，试验段的气流速度和马赫数均减小，静压和静温均上升。这是由于焦耳热的作用，从负载系数可以看出，焦耳热的作用远大于洛伦兹力作用，焦耳热的作用是主导流场参数变化的主要因素，洛伦兹力的作用相对较小。

3 数值模拟

3.1 计算模型

流体采用黏性可压缩流，添加电磁源项的Navier-Stokes方程组写作

(15)

(16)

(17)

电势泊松方程组

(18)

式中：β为霍尔参数，φ为电势。

通过添加电磁源项的Navier-Stokes方程耦合电势泊松方程建立磁流体动力模型。流体模型采用Splart-Allmaras湍流模型，通过用户自定义函数UDF添加体积力源项j×B和能量源项α·j·E，并耦合电势方程进行求解。根据试验条件对磁流体通道网格划分如图8所示，网格规格为80×200，对电极边角和附面层进行加密处理。流场边界条件为：入口压力远场边界条件，入口马赫数3.3，静压为500 Pa，静温为90 K；出口为压力出口；壁面采用无滑移绝热边界条件。电势边界条件为：通道进出口和壁面电流通量为零，即

j·n=0，上壁面1～3 cm处为阳极，下壁面1～3 cm 处为阴极，电极电势为固定值。

3.2 数值模拟结果

图9为不加磁场时流场马赫数、电势以及电流密度分布图，图中B为磁感应强度，U为直流放电电压，σ为电导率，出口的马赫数3.285，静压为510 Pa，速度为627 m/s，与试验结果基本相符。由于进口条件设置为压力远场条件，进口处出现微弱的斜激波，但是作用区域很小，不影响整个流场的马赫数分布，整个流场马赫数分布均匀。电势分布对称，电流分布在整个通道内存在梯度，电极覆盖下的电流密度大于两侧的电流密度，在电极的4个边角处电流发生集中。同时从电流流线可以看出，电流基本不存在沿通道方向分量，说明超声速气流对电流干扰比较小。

图10为磁流体加速时，流场马赫数、电势、电流及洛伦兹力F分布图，计算结果显示：出口马赫数为3.01，静压为628 Pa，速度为621 m/s，静压值与试验测量结果相吻合，速度与准一维方程计算的结果基本相符，出口马赫数比准一维方程的计算结果略高，主要原因在于主流区域的温升

存在较大的差异，在一维模型中假设焦耳热量均匀地分布在通道内。二维数值模拟中，热量主要集中在电极边角处，主流区域的温升较小，因此在出口速度基本一样的前提下，出口马赫数较高。

从图10(a)马赫数分布可以看出，马赫数沿通道方向逐渐减小，由于霍尔效应的影响，流场中马赫数分布不均，通道上半部分马赫数小于下半部分马赫数。同时，在阳极的左端和阴极的右端电流密度比较集中，局部热效应增强，诱导产生了一道弱斜激波。从图10(b)电势分布可以看出，电势在左右两侧分布不均匀，主要是由于等离子体在磁场中受洛伦兹力作用。从图10(d)洛伦兹力分布可以看出，在近壁面处带电粒子将向上下壁面处运动，由于壁面处电流通量为零，壁面上开始累积正负电荷，在阳极左侧和阴极右侧累积正电荷，因而电势升高，阳极右侧和阴极左侧累积负电荷，电势降低。从图10(c)电流密度分布可以看出，磁场的作用使得电流密度在阳极左端和阴极右端集中，过高的电流密度也导致了局部的静温过高，容易造成电极烧蚀。从图10(d)可以看出，受霍尔效应作用主流区的洛伦兹力的方向发生偏转，产生了向上的分量，不利于流场的加速。

图11为磁流体减速作用时流场马赫数、电势、电流及洛伦兹力分布图，计算结果显示：出口马赫数为2.81，静压为708 Pa，速度为606 m/s，静压值与试验测量结果基本吻合，速度与准一维方程计算的结果基本相符，马赫数比准一维方程分析结果略高。主要的原因是数值模拟时焦耳热造成的温度上升主要集中在电极边角区域，主流区的温升较小，因而马赫数较高。

流场马赫数沿通道逐渐减小，因霍尔效应和电极边角处热效应诱导产生的斜激波，流场马赫数分布不均，由于改变磁场方向，霍尔效应方向也发生改变。流场中的马赫数、电势以及电流密度分布均与加速时相反。通道内上半部分马赫数较高，电势在阳极右侧与阴极左侧较高，电流密度在其附近相对集中，减速洛伦兹力产生向上分量。

4 结 论

1) 在磁场约束下，电容耦合射频-直流组合放电能够在Ma=3.5流场中产生大体积均匀电流，电流密度约为1 000 A/m2左右，电导率约为0.015 S/m。

2) 由于焦耳热作用显著，加速洛伦兹力作用时静压升高了130 Pa，减速洛伦兹力作用时静压升高了200 Pa。

3) 磁流体流动控制过程中，仅有不足10%的能量在磁流体通道内发生作用。

4) 数值模拟结果显示，在试验条件下，加速洛伦兹力作用时静压升高了128 Pa，减速洛伦兹力作用时静压升高了208 Pa，与试验结果基本吻合。

[1] SU C B, LI Y H, CHEN B Q, et al. Experimental investigation of MHD flow control for the oblique shock wave around the ramp in low-temperature supersonic flow[J]. Chinese Journal of Aeronautics, 2010, 22(1): 22-32.

[2] 王振国, 梁剑寒, 丁猛, 等. 高超声速飞行器动力系统研究进展[J]. 力学进展, 2009, 39(6): 716-739. WANG Z G, LIANG J H, DING M,et al. A review on hypersonic airbreathing propul sion system[J]. Advanced in Mechanics, 2009, 39(6): 716-739 (in Chinese).

[3] 郑小梅, 吕浩宇, 徐大军, 等. MHD加速器模式磁控进气道的优化设计[J]. 航空学报, 2010, 31(2): 223-230. ZHENG X M, LU H Y, XU D J, et al. Optimization of accelerator mode MHD controlled inlet[J]. Acta Aeronoutica et Astronautica Sinica, 2010, 31(2): 223-230 (in Chinese).

[4] KURANOV A L, KUCHINSKY V V, SHEIKIN E G. Scramjet with MHD control under “Ajax” concept. requirements for MHD Systems：AIAA-2001-2881[R]. Reston：AIAA, 2001.

[5] KURANOV A L, SHEIKIN E G. MHD control on hypersonic aircraft under “AJAX” concept. possibilities of MHD Generator：AIAA-2002-0490[R]. Reston：AIAA, 2002.

[6] DAVID M W, NEDUNGADI A. Plasma aerodynamic flow control for hypersonic inlets：AIAA-2004-4129[R]. Reston：AIAA, 2004.

[7] BRICHKIN D I, KURANOV A L, SHEIKIN E G. The potentialities of MHD control for improving scramjet proformance：AIAA-1999-4969[R]. Reston：AIAA, 1999.

[8] SHNEIDER M N, MACHERET S O, MILES R B. Nonequilibrium magnetohydrodynamic control of scramjet inlet：AIAA-2002-2251[R]. Reston：AIAA, 2002.

[9] BOBASHEV S V, GOLOVACHOV Y P, VANWIE D M. Deceleration of supersonic plasma flow by an applied magnetic field：AIAA-2002-2247[R]. Reston：AIAA, 2002.

[10] BOBASHEV S V, MENDE N P, SAKHAROV V A, et al. MHD control of the separation phenomenon in a supersonic Xenon plasma flow：AIAA-2003-168[R]. Reston：AIAA, 2003.

[11] BOBASHEV S V, GOLOVACHOV Y P, VAN WIE D M. Deceleration of supersonic plasma flow by an applied magnetic field[J]. Journal of Propulsion and Power 2003, 19(4): 538-546.

[12] 李益文, 李应红, 张百灵, 等. 基于激波风洞的超声速磁流体动力技术试验系统[J]. 航空学报， 2011, 32(6): 1015-1024. LI Y W, LI Y H, ZHANG B L, et al. Supersonic magnetohydyodynamic technical experimental system dased on shock tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(6): 1015-1024 (in Chinese).

[13] NISHIHARA M. Low-temperature supersonic flow control using repetitively pulsed MHD force[D]. Columbus: The Ohio State University, 2006.

[14] NISHIHARA M, BRUZZESE J, ADAMOVICH I V. Experimental and computational studies of low-temperature M=4 flow deceleration by Lorentz gorce: AIAA-2007-4595[R]. Reston：AIAA, 2007.

[15] NISHIHARA M J, RICH W, LEMPERT W R, et al. MHD flow control and power generation in low-temperature supersonic flows: AIAA-2006-3076[R]. Reston：AIAA, 2006.

[16] MEYER R, CHINTALA N, BYSTRICKY B, et al. Lorentz force effect on a supersonic ionized boundary layer: AIAA-2004-0510[R]. Reston：AIAA, 2004.

[17] UDAGAWA K, KAMINAGA S, ASANO H, et al. MHD boundary layer flow acceleration experiments: AIAA-2006-3233[R]. Reston：AIAA, 2006.

[18] UDAGAWA K, KAWAGUCH K, SAITO S, et al. Experimental study on supersonic flow control by MHD interaction: AIAA-2008-4222[R]. Reston：AIAA, 2008.

[19] MACHERET S O, SHNEIDER M N, MILES R B. External supersonic flow and scramjet inlet control by MHD with electron beam ionization: AIAA-2001-0492[R]. Reston：AIAA, 2001.

[20] LEONOV S B, YARANTSEV D A. Near-surface electrical discharge in supersonic airflow: properties and flow control[J]. Journal of Propulsion and Power 2008, 24(6): 1168-1181.

(责任编辑：张晗)

＊Corresponding author. E-mail: lee_yiwen@163.com

Test and numerical simulation on magneto-hydrodynamic flow control with nonequilibrium ionization

LI Yiwen1,2,*, FAN Hao2, ZHANG Bailing2, WANG Yutian2, DUAN Chengduo2, GAO Ling2,ZHUANG Zhong2, HE Guoqiang1

1.ScienceandTechnologyonCombustion,InternalFlowandThermo-StructureLaboratory,AstronauticsSchool,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.ScienceandTechnologyonPlasmaDynamicsLaboratory,AirForceEngineeringUniversity,Xi’an710038,China

In order to study the mechanism of MHD flow control, an experimental system based on MHD technology is established.Ma=3.5 flow is ionized with radio frequency-direct current composite discharge to acquire the bulk mass and uniform current. The research on accelerating/decelerating in different directional magnetic field is implemented, and the effect of MHD control is analyzed by static pressure of experimental section and quasi-one-dimensional model. The numerical simulation of MHD flow control with the MHD model is carried out based on the Navier-Stokes equation coupled with the electronmagnetism source term. The result shows that the bulk mass and the uniform current inMa=3.5 flow can be acquired with radio frequency-direct current composite discharge, and the conductivity is 0.015 S/m. As a result of joule heat, the static pressure rises 130 Pa with accelerating Lorentz force, and 200 Pa with decelerating Lorentz force. There is less than 10% energy is spent on the MHD flow control. The result of numerical simulation shows that under the experimental condition, the static pressure rises 128 Pa with accelerating Lorentz force, and 208 Pa with decelerating Lorentz force. The simulation results agree basically with the experiment results.

plasma; MHD flow control; supersonic; nonequilibrium ionization; conductivity

2016-04-26； Revised：2016-05-26； Accepted：2016-06-12； Published online：2016-07-01 10:19

URL：www.cnki.net/kcms/detail/11.1929.V.20160701.1019.002.html

s：National Natural Science Foundation of China (51306207,11372352)； China Postdoctoral Science Foundation (2016M590972)； Natural Science Foundation Research Project of Shaanxi Province (2015JM5184)

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0188

2016-04-26； 退修日期：2016-05-26； 录用日期：2016-06-12； 网络出版时间：2016-07-01 10:19

www.cnki.net/kcms/detail/11.1929.V.20160701.1019.002.html

国家自然科学基金 (51306207、 11372352)； 中国博士后科学基金(2016M590972)； 陕西省自然科学基础研究计划 (2015JM5184)

＊通讯作者.E-mail: lee_yiwen@163.com

李益文， 樊昊， 张百灵， 等． 超声速非平衡电离磁流体流动控制试验和数值模拟 [J]． 航空学报, 2017, 38(3): 120368. LI Y W， FAN H, ZHANG B L, et al. Test and numerical simulation research on magneto-hydrodynamic flow control with nonequilibrium ionization[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 120368.

V211.73

A

1000-6893(2017)03-120368-10