抛弃式探头下沉运动数值计算的网格划分方法研究
2017-11-17陈振涛王晓蕾
陈振涛,刘 凤,王晓蕾,叶 松
(国防科技大学 气象海洋学院,江苏 南京 211101)
抛弃式探头下沉运动数值计算的网格划分方法研究
陈振涛,刘 凤*,王晓蕾,叶 松
(国防科技大学 气象海洋学院,江苏 南京 211101)
各类抛弃式探头下沉运动的数值计算研究都需要对探头表面和整个计算域进行网格划分的前处理过程,选择不同的网格划分方法和划分精度,会影响数值计算速度和计算精度,最终生成的网格质量决定了计算结果的收敛性和准确性。针对抛弃式探头的复杂结构,对比了两种网格划分方法、三种网格划分精度,完成探头计算区域的网格划分,采用k-ε湍流模型,进行抛弃式探头下沉运动的数值计算,并将计算结果与水箱和水库实验结果进行对比,验证了混合网格划分方法和普通精度网格对抛弃式探头下沉运动数值计算的适用性,研究结果对类似较为复杂结构的水下运动体的数值计算前处理过程具有一定的参考和借鉴意义。
抛弃式探头;数值计算;网格划分;混合网格
目前针对各类抛弃式探头下沉运动的数值计算,主要采用 CFD(Computational Fluid Dynamics,计算流体动力学)技术[1-3],其处理过程主要包括前处理、有限元计算以及后处理三部分,其中网格划分是前处理过程的主要工作,较为繁琐和耗时,但影响到有限元计算成功的关键[4]。
不同的流体问题需要采用不同的数值求解方法,相应的网格形式也有所不同,网格生成的类型和数量会影响计算速度和计算精度,网格质量的好坏则直接影响到计算结果的收敛性和准确性[5]。
针对抛弃式探头(本文特指NMOHEMS[6]探头,以下同)的复杂结构,对比不同网格划分方案,选择最佳的网格划分方法和划分精度,完成探头表面和计算区域的网格划分,以开展探头下沉运动数值计算。
1 网格划分方法
1.1 网格划分技术
利用GAMBIT前处理软件[7],其可划分的网格类型主要包括结构网格和非结构网格。其中结构网格[8]结构清晰,网格节点排列有序,相邻节点之间的关系明确,所有节点周围网格的拓扑结构都相同。2D中表现为四边形网格,3D中为六面体网格。结构网格处理简单的几何体网格时十分有效,但是不适用于复杂外形的几何体网格生成。
非结构网格[9]消除了网格节点的结构性约束,可以任意分布其网格节点和单元,方便灵活地处理一些复杂的边界情况。但需要控制好网格的大小和节点密度,以保证网格的质量。非结构网格的主要缺点是计算效率较低,特别是对计算机内存的要求较高,相应计算时间较长,所以其普适性受到制约。
针对复杂外形的网格问题,近年来发展起来的还有一种自适应笛卡尔网格[10],根据几何体表面和流场特点,在边界等局部区域不断细化加密网格,以实现较高精度的一种非均匀网格。自适应笛卡尔网格的生成过程省时方便且数据结构较为简单,但是外形描述的网格精度较低,无法做到贴体网格,对于一些边界层流动问题,无法满足计算要求。三种网格方法生成的2D网格对比,如图1所示。
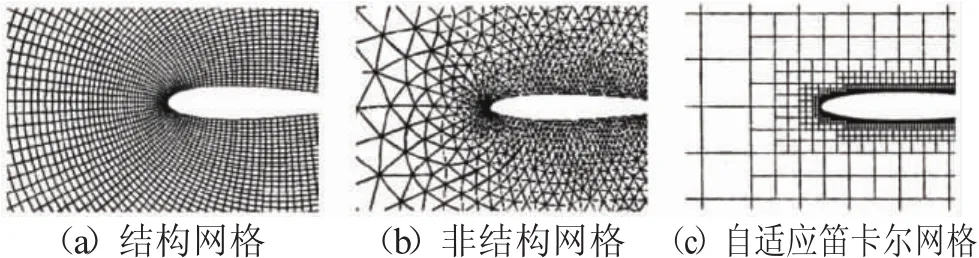
图1 三种网格方法生成的2D网格对比
在解决抛弃式探头类复杂外形网格的生成问题时,可以采用将结构网格和非结构网格相结合的混合网格方法[11],即在几何体的复杂表面区域采用非结构网格,而在远离几何体的区域采用结构网格,这样生成的网格质量较高,同时保证较高的计算效率。
1.2 计算域及边界条件
探头的整个计算域由进流、出流、壁面和控制域边界组成,图2为Z=0时计算区域模型的截面。图中,L为探头的长度,R为探头最大半径,X为水平方向,Y为重力加速度的反方向。
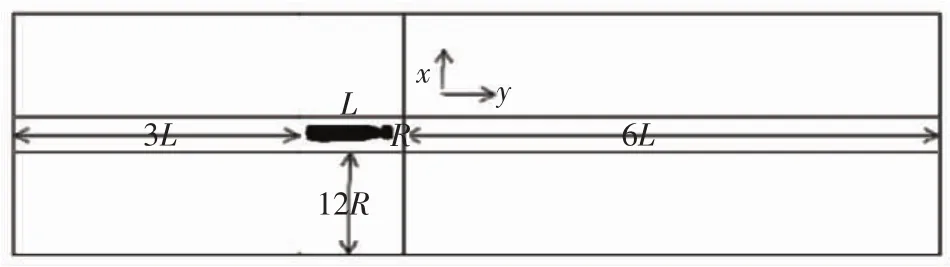
图2 探头模型计算域示意图
各边界条件如下:采用速度进口边界条件,入流断面为均匀来流;采用压力出流边界条件,认为湍流已经达到平衡,以加快收敛速度;探头模型表面和计算域的其余外边界均设为无滑移壁面;模型近壁采用标准壁面函数进行处理。
其中,速度进口的湍流参数项选择为湍流强度I和特征长度l(Intensity and Length Scale)方法。充分发展的管内流动中,湍流强度I可以利用经验公式[12]给出,湍流强度是一个很小的量,通常在1%~10%范围内,对于边界条件为外部入流,其计算公式为:
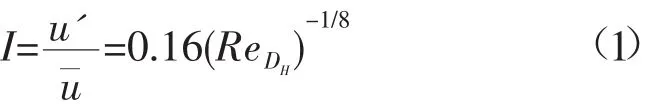
式中:u'为速度脉动;u¯为平均速度;,ReDH为入口边界处的雷诺数。根据上式,当雷诺数为104时,湍流强度I约为5.06%。
特征长度l是与湍流中大涡尺度相关的物理量,圆管内流动时与管长相关,其计算公式[12]为:

式中:L为圆管长度,本文中探头运动为外部绕流问题;L即为探头沿水流方向的长度。
1.3 计算域的网格划分方法
因为探头外形较为复杂,无法采用结构网格的划分方法,采用完全非结构网格和混合网格两种方法进行比较。
完全非结构网格的划分方法,在探头表面划分边界层,其余区域均划分为四面体形的非结构网格,探头附近区域网格较密集,远离探头区域网格较稀疏,模型总网格数为2 546 718个。
采用混合网格划分计算域,在探头表面附近划分边界层,划分为三棱柱形的半结构网格;边界层外的探头附近区域,网格类型采用四面体形的非结构网格;远离探头区域则划分为六面体形的结构网格。进一步加密导流腔和尾翼附近网格,模型总网格数为1 964 509个。
两种方法的探头表面网格均采用三角形非结构网格进行划分,如图3所示;计算域的纵向对称面网格分布如图4所示。

图3 探头表面的网格划分
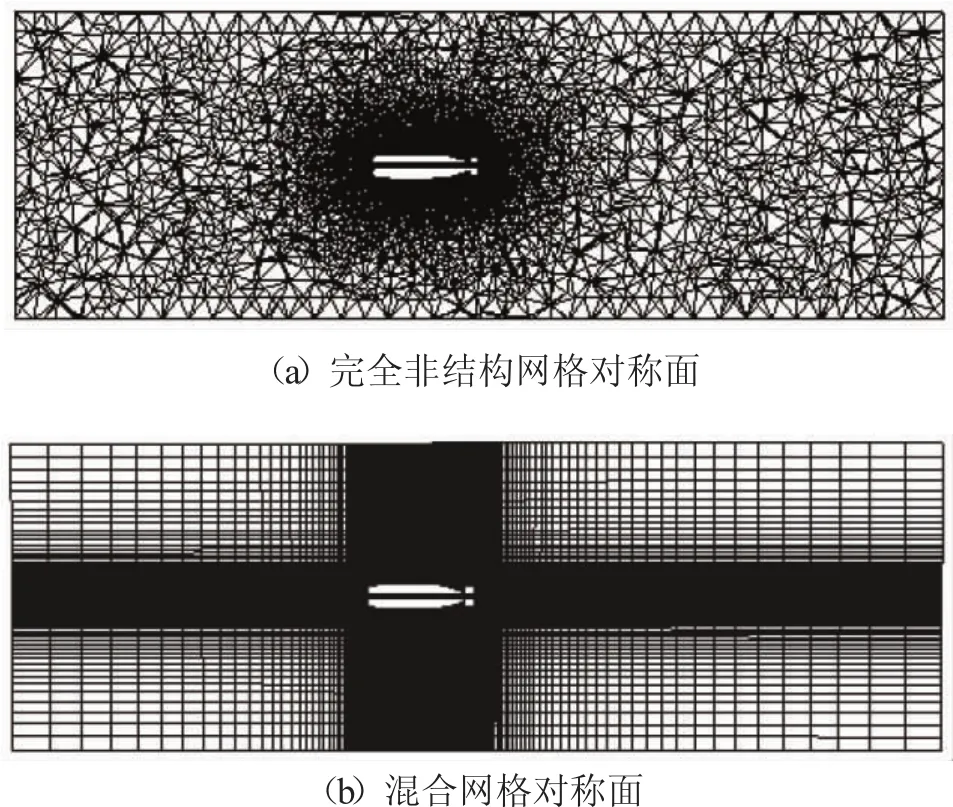
图4 两种网格的纵向对称面网格分布
选择Realizable k-ε湍流模型,分别采用上述两种网格对流场进行计算,网格数、迭代次数n和计算的阻力系数Cd如表1所示。其中实验结果采用实验室玻璃水箱,高精度调整探头质量,利用高速摄像和图像处理技术,经过详细的误差分析和修正后,得到多个较小质量探头的下沉运动的下沉曲线和极限速度[13]。
从表中可以看到,混合网格的网格数比完全非结构网格减少22.86%,迭代次数也相应地减少,并且随着速度的增加,迭代次数减少得更加明显,而两者的计算结果非常接近。证明了混合网格的计算速度和计算效率比完全非结构网格有相当大的提高,同时保证了计算结果的稳定性。
1.4 网格划分精度
网格划分精度的不同对占用内存、计算时间和计算结果有较大的影响。采用混合网格的划分方法,设定来流速度分别为0.1 m/s,0.2 m/s,0.3 m/s,选择以下3种网格精度进行比较:(a)较稀疏(Coarse mesh)、(b)普通(Nominal mesh)、(c)较精密(Fine mesh)。
三种网格精度的最小、最大网格尺寸、网格数、迭代次数和计算的阻力系数比较如表2所示。

表2 三种网格精度及阻力系数的比较
表中可以看到,网格较稀疏时的网格数最小,迭代次数最少,但是计算的阻力系数结果误差偏大;网格较精密时的网格数最大,迭代次数最多,且成指数倍增加,计算耗时较长,且容易产生内存溢出;普通网格精度的计算耗时较短,与较精密网格的计算结果相差不大,所以最终选定网格精度为普通精度。
1.5 求解控制参数的设置
采用有限体积法离散控制方程和湍流模型,压力方程的离散格式包括:Standard、PRESTO、Second Order和Body Force四种,其中PRESTO主要应用于高速流动,特别是含有旋转及高曲率的情况下;Second Order用于可压流动;Body Force用于含有大体力的流动;所以采用Standard离散格式进行离散压力方程。
动量方程、湍流方程和雷诺应力方程均采用二阶迎风格式进行离散,压力速度耦合迭代采用SIMPLEC算法,欠松弛因子取为1.0。
此外,求解过程中需要监视各变量的残差,残差收敛的精度越高,湍流发展越充分,计算的结果也越精确。残差收敛精度的选取对计算时间和计算精度的影响也较为明显,所以在选择时应当尽量满足湍流充分发展。选择以下3种残差收敛精度进行比较:(a)10-3,(b)10-4,(c)10-5。
分别将来流速度设为 0.1 m/s,0.5 m/s,1.0 m/s,1.5 m/s和2.0 m/s进行计算,迭代次数和计算得到的阻力大小如表3所示。
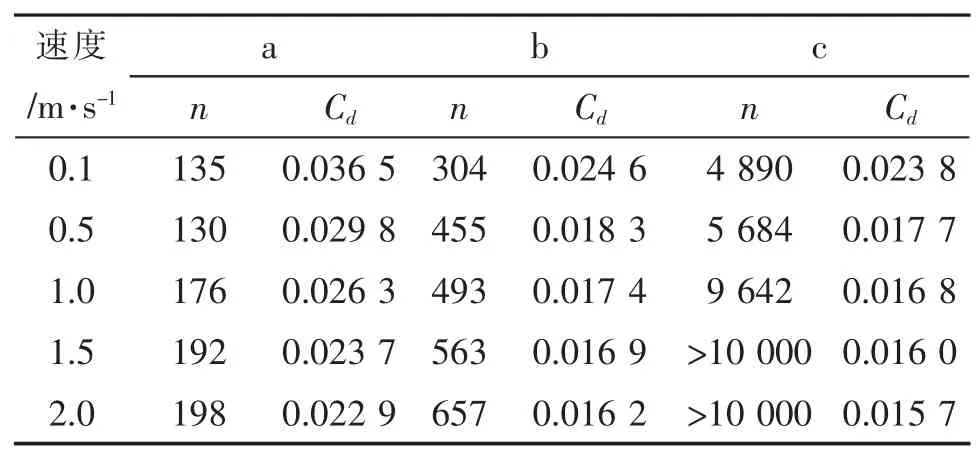
表3 三种残差收敛精度时的迭代次数和阻力系数比较
表中可以看到,残差收敛精度为10-3时的迭代次数较少,但是阻力系数的计算结果偏大;残差收敛精度为10-4时的迭代次数都非常大,其中“>10 000”是指迭代10 000次时残差仍然没有达到指定的收敛精度,湍流发展较为充分,所以阻力系数的计算结果较为精确;残差收敛精度为10-4时的迭代次数较少,而阻力系数的计算结果与10-5时较为接近,所以最终选定残差收敛精度为10-4时。
2 计算结果及分析
采用混合网格划分方法、普通网格精度,对探头表面和计算域进行网格划分,选择Realizable k-ε湍流模型,采用Standard离散格式离散压力方程,采用二阶迎风格式离散动量方程、湍流方程和雷诺应力方程,SIMPLEC算法进行压力速度耦合迭代处理,残差收敛精度为10-4,对探头及其计算域进行数值计算。
图5给出了水箱实验得到的不同质量探头,极限速度对应的雷诺数与阻力系数的关系;*为实验结果,□为数值计算结果,雷诺数范围在104左右。
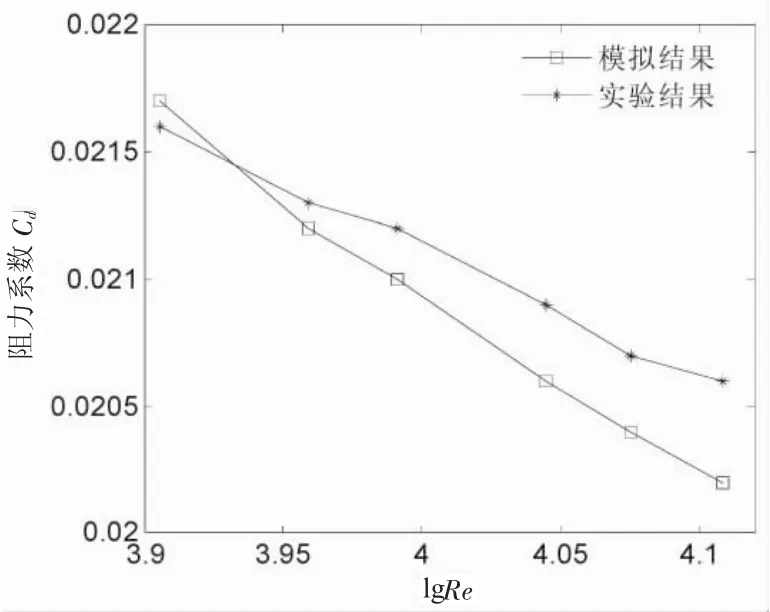
图5 雷诺数与阻力系数的关系
可以看到两个结果的变化趋势较为一致,阻力系数均随着雷诺数的增大而减小,模拟结果整体均小于实验结果,并且随着雷诺数的增加,两者的差别逐渐增大。分析可能有两部分原因,一是建立的数值计算模型较为理想和光滑,造成了计算得到的阻力偏小;二是没有考虑探头下沉时水箱中存在的波动干扰等因素的影响。
表4为六种不同质量探头对应阻力系数的数值计算结果与水箱实验结果对比关系。
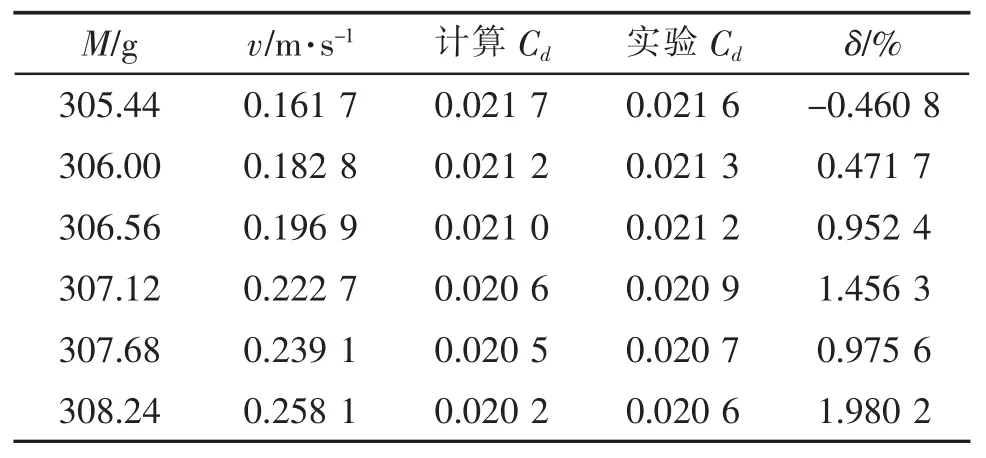
表4 数值计算结果与水箱实验结果对比
可以看到,不同质量时两个结果都非常接近,误差δ控制在2%以内,验证了雷诺数范围在104左右时,网格划分方法和数值计算模型的正确性和可行性。
此外,还进行了水库实验,对较大质量探头的下沉运动进行测量,得到0.48 kg探头的极限速度为1.92 m/s,雷诺数在105范围,实验得到的测量结果经过水面风速和装置摩擦等误差处理后,得到测量修正值,三者的对比情况见表5。
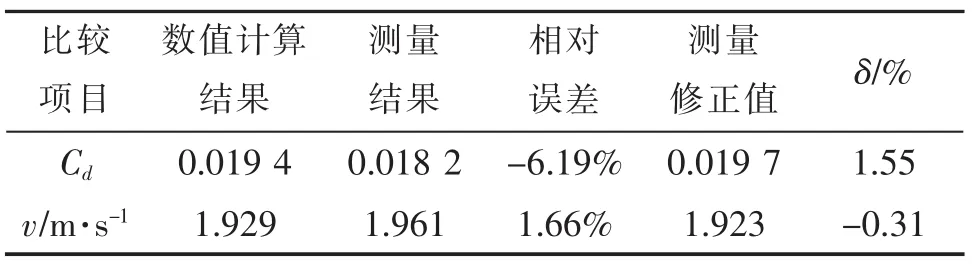
表5 水库测量结果、修正值与数值计算结果对比
表中可见,经过误差处理后的测量修正值与数值计算结果较为接近,阻力系数相对误差为1.55%,极限速度的相对误差只有-0.31%,最大误差均控制在2%以内,验证了雷诺数范围在105左右时,网格划分和数值计算模型的正确性和可行性。
图6~图7分别给出了v为0.001 m/s,0.01 m/s,0.1 m/s和2.0 m/s时探头纵向对称面的压力分布和y+分布情况。
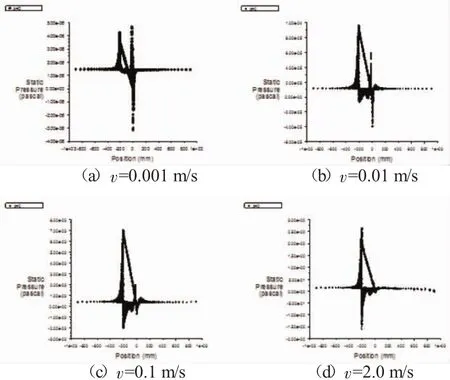
图6 不同速度时纵向对称面的压力分布曲线
从图中可以看到,不同速度时纵向对称面上的高低压分布情况基本一致,只是压力的强度和范围有所区别。流场在靠近探头头部(-200 mm处)时压力值迅速增大,之后跟随一个低压区,压力又迅速减小;尾翼前端(-20 mm处)因为尾翼的阻碍作用,也形成一个明显的高压区,并且跟随一个小的低压区;通过尾翼后在尾翼后端(0 mm处)形成一个较小的高压区。v=0.001 m/s时探头头部的压力强度较小,跟随的低压区也不明显,但是尾翼前端的高压区和低压区较为明显,强度甚至超过探头头部;v=0.01 m/s时探头头部的压力强度增大,跟随低压区的强度和范围都有所增大,尾翼后端的高压区也稍有增强;v=0.1 m/s时探头头部的高压区和跟随低压区的压力强度和范围继续增大,尾翼前后的高压区和跟随低压区的增长速度相对减弱;v=2.0 m/s时探头头部和跟随低压区的压力强度和范围继续增大,尾翼前后的高低压区相对减弱得较为明显。
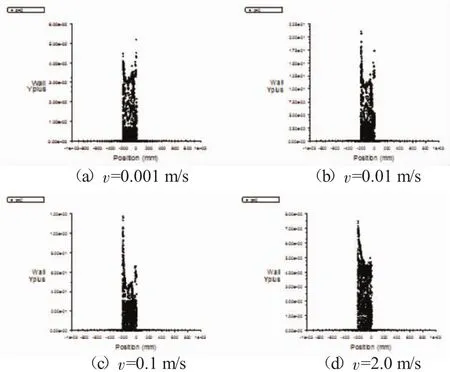
图7 不同速度时纵向对称面上的y+分布曲线
从不同速度时纵向对称面上的y+分布可以看到,横坐标在-200 mm处,即探头头部位置的y+值最大,之后由于导流腔和收缩段的影响y+值迅速减小,到-20 mm处,即尾翼前部位置时y+值又有所增加;v=0.001 m/s时探头壁面的y+最大值只有0.05左右,v=0.01 m/s时探头壁面的y+最大值约为0.2,v=0.1 m/s时探头壁面的y+最大值约为1.2,v=2.0 m/s时探头壁面的y+值达到8;并且随着速度的增大,探头尾部的y+值的增幅相对较小。0~2.0 m/s范围内探头表面的y+值均小于8,即探头表面一直处于粘性底层,证明了边界层网格划分和近壁处理能够真实反应探头表面边界层的流动情况。
不同速度时探头的周围流场分布情况有所差异,图8~图9分别给出探头在不同速度时周围的压力和速度分布情况。可以看到,混合网格能够较为完整地显示不同速度时,探头周围流场的压力、速度分布情况。
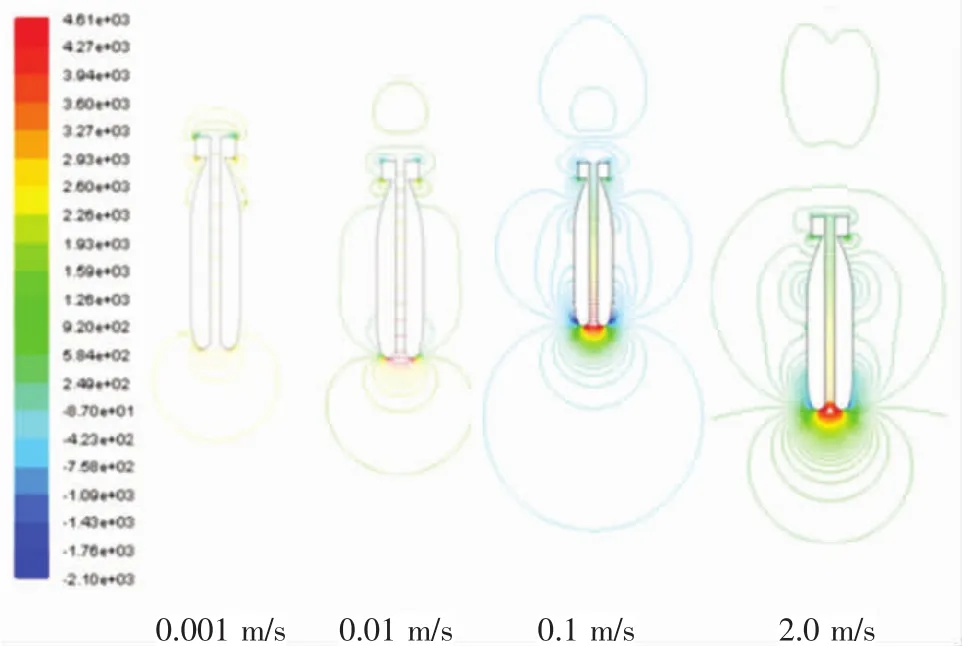
图8 不同速度时探头周围流场的压力分布图
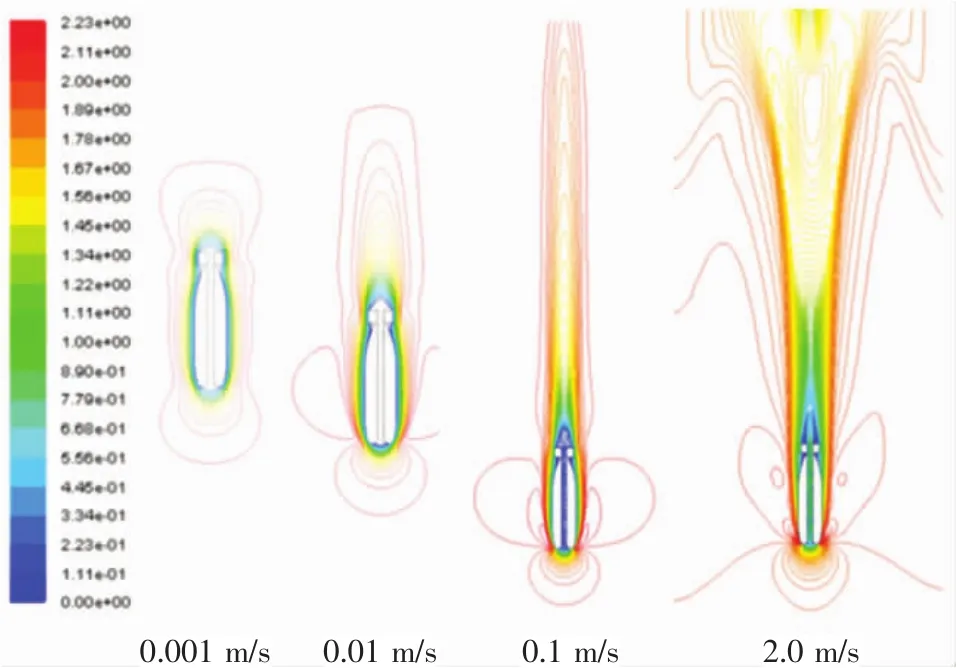
图9 不同速度时探头周围流场的速度分布图
均匀来流均受到了探头的阻碍,在靠近探头头部附近形成了一个局部静压高于来流静压的高压区,探头近表面附近的流场速度小于外围流场速度;速度为0.001 m/s时,压力和速度较小,尚未出现分离现象,也未产生湍流涡旋,所以此时探头周围仍然是层流状态;速度为0.01 m/s时,各流场分布有所加强,压力和速度开始出现分离现象,探头尾部出现较为明显的尾涡区,但是强度和范围较小,说明此时探头周围流场已由层流进入转捩区;速度为0.1 m/s时,压力和速度的流场分离现象更加明显,尾涡区的强度和范围明显增强,说明此时流场的湍流得到较强的发展;速度为2.0 m/s时,流场分布进一步增强,湍流已得到充分发展,速度场经过上表面的阻碍后反射,与原流场进行叠加,使得整个计算域的流场分布更加复杂。
3 结束语
本文根据抛弃式探头特点,对网格划分方法和划分精度进行了讨论,计算其不同下沉速度时对应的阻力系数;最后对计算结果进行简单分析,并分别与水箱和水库实验结果进行对比,得到主要结论如下:
(1)在解决抛弃式探头类的复杂外形网格生成问题时,可以采用结构网格和非结构网格相结合的混合网格方法,这样生成的网格质量较高、网格数较少、运算速度较快且计算结果稳定。
(2)网格划分精度对占用内存、计算时间和计算结果有较大的影响,为保证计算结果更高的准确性,应根据计算机内存和运算性能选择较高的网格精度。抛弃式探头选用普通网格精度的网格数适中,计算耗时较短,计算的阻力系数结果与实验结果较为接近。
(3)CFD仿真计算结果除了与网格划分相关,还与选择的湍流模型、离散求解方案,压力速度耦合迭代算法,以及残差收敛精度等有关。
有限元网格生成技术还有曲面网格生成、并行网格生成等很多方法,针对不同问题和需求,选择的网格划分方法也不尽相同,需要在实际应用中不断总结经验才能快速地得到最佳的网格划分模型。
[1]肖鸿,刘长根,陶建华.抛弃式温盐探头阻力系数的数值模拟及其实验验证[J].海洋技术,2006,25(3):35-37.
[2]孙涛,黄银水,陶建华.抛弃式温盐探头运动状态的数值模拟及其实验验证[J].海洋通报,2002,21(2):69-76.
[3]刘宁,张瑞,陈文义,等.XCP投弃式海洋探头阻力系数数值计算及试验研究[J].海洋技术,2010,29(4):12-14.
[4]杜平安.有限元网格划分的基本原则[J].机械设计与制造,2000(1):34-36.
[5]邢静忠,李军.ANSYS的建模方法和网格划分[J].中国水运(学术版),2006,9(6):116-117.
[6]叶松,王晓蕾,焦冰,等.NMOHEMS的概念与设计[J].海洋技术,2010,29(1):28-31.
[7]Bhutta M M A,Hayat N,Bashir M H,et al.CFD applications in various heat exchangers design:A review[J].Applied Thermal Engineering,2012,32:1-12.
[8]常煜,张志荣,赵峰.多块结构化网格在含附体水面船模粘性流场数值计算中的应用[J].船舶力学,2004,8(1):19-25.
[9]何晓聪,曹红松,赵捍东,等.弹箭外部绕流数值仿真中网格的选择[J].弹箭与制导学报,2009,29(2):191-194.
[10]韩玉琪,张常贤.基于自适应笛卡尔网格的可压缩黏性流动数值模拟[J].科学技术与工程,2015(24):115-120.
[11]吴明.舰船不同浮态下阻力的CFD方法研究[D].大连:海军大连舰艇学院,2009.
[12]王福军.计算流体动力学分析-CFD软件原理与应用[M].北京:清华大学出版社,2004.
[13]陈振涛,钟中,叶松,等.NMOHEMS探头模型的制作及实验方法研究[J].实验流体力学,2013(2):100-105.
Research on the Mesh Dividing Method for Expendable Probe Sinking Simulation
CHEN Zhen-tao,LIU Feng,WANG Xiao-lei,YE Song
Institute of Meteorology and Oceanography,National University of Defense Technology,Nanjing 211101,Jiangsu Province,China
The pre-treatment process with mesh dividing is required for the surface of probe and the whole computational field when conducting expendable probe sinking numerical simulation.Different meshing methods and meshing densities will affect the calculation speed and accuracy,and the quality of the resulting mesh determines the convergence and accuracy of the calculation results.In view of the complex structure of the expendable probe,two meshing methods and three mesh densities are compared,with the mesh division of the probe computational field completed.Numerical simulation of the probe sinking motion is carried out by selected turbulence model,whose results are compared with the experimental results of the laboratory pool and lake.This paper verifies the applicability of the hybrid mesh dividing method and the general precision of mesh density in expendable probe sinking numerical simulation.The results of the study can be used as a reference for the numerical simulation of underwater moving bodies with complex structures.
expendable probe;numerical simulation;mesh dividing;hybrid mesh
P716+.1
A
1003-2029(2017)05-0032-06
10.3969/j.issn.1003-2029.2017.05.006
2017-05-31
国家自然科学基金资助项目(41406107)
陈振涛(1983-),男,博士,讲师,研究方向为海洋探测技术。E-mail:czt1212@126.com
刘凤(1983-),女,硕士,讲师,研究方向为海洋探测装备。E-mail:li_ufeng@126.com
