基于磁偶极子的磁场梯度张量局部缩并及试验验证

江胜华，侯建国，何英明，汪时机

（1. 西南大学 工程技术学院，重庆 400715；2. 南洋理工大学 土木与环境工程学院，新加坡 639798；3. 武汉大学 土木建筑工程学院，武汉 430072）

基于磁偶极子的磁场梯度张量局部缩并及试验验证

江胜华1,2，侯建国3，何英明3，汪时机1

（1. 西南大学 工程技术学院，重庆 400715；2. 南洋理工大学 土木与环境工程学院，新加坡 639798；3. 武汉大学 土木建筑工程学院，武汉 430072）

基于磁偶极子的磁场梯度张量缩并理论虽然可较好地描述磁源，不受测量系统的朝向的影响，但在实际的磁场梯度张量测量中通常仅可测得部分磁场梯度参数，没有获得磁场梯度张量中的所有张量分量，如何有效利用这些部分磁场梯度参量，已成为目前磁场梯度张量缩并理论及在磁场定位的应用中亟需解决的问题。基于磁偶极子理论提出磁场梯度张量局部缩并的方法，给出磁场梯度张量的局部模量的概念，分析了磁场梯度张量的局部模量及相关参数的三维空间分布规律，结果表明：局部模量CXY及kXY值随着ϑ先增大后减小，在ϑ=39°时取最大值，在ϑ=90°时取最小值；局部模量CZ及kZ值随着ϑ先减小后增大，在ϑ=63°时取最小值，在ϑ=0°时取最大值。提出磁场梯度张量局部模量中重要参数的近似计算公式，并通过试验进行验证。试验结果表明，试验值与理论计算值基本一致，可为磁场梯度张量局部缩并理论的应用提供依据和参考。

磁偶极子；磁场梯度张量；局部缩并；局部模量

基于磁场梯度张量的地磁异常反演，主要基于磁感应强度的梯度张量、张量不变量及张量的模量等，可更好地描述磁源体的边界、位置、磁化形态及走向等，受地磁场的影响较小，受环境磁场的干扰影响亦较小，提高了对磁源体的探测效率和分辨率[1-3]，可广泛用于定位与导航、工程物探、无损检测等[4-7]。磁场梯度张量缩并将磁场梯度张量中的9个张量元素缩并为1个标量（即模量）[8-9]，该标量与磁源体的磁矩和位置直接相关，可更便捷地反映磁源体的相对距离和几何边界，不受磁场传感探头朝向的影响。全张量磁场梯度测量系统的发展则为磁场梯度张量缩并理论的实际应用提供了传感硬件上的支撑。另一方面，在磁场梯度张量的实际测量中，通常采用多个三轴磁传感器组合形成磁场梯度张量测试系统，间接测量得到磁场梯度张量，但由于高精度磁传感设备高昂的价格及在数量和空间布置等多方面的限制，很多情况下无法测量得到磁场梯度张量中的所有张量分量，仅可测得部分磁场梯度参量。如何有效利用这些部分磁场梯度参量，并应用在基于磁场梯度张量的磁场定位及相关领域，成为目前磁场梯度张量缩并定位理论中亟需解决的问题。

本文基于磁偶极子提出磁场梯度张量局部缩并的方法，给出磁场梯度张量的局部模量的概念，并推导磁场梯度张量局部缩并的公式，分析磁场梯度张量局部缩并的空间分布规律，给出相关参数的近似计算公式，并采用试验进行验证。

1 基于磁偶极子的磁场梯度张量局部缩并

当磁性体至测点的距离超过磁性体长度的25倍时，可将磁性体视为一个磁偶极子模型[8]。磁性体在测点的磁感应强度的矢量为：

式中，0μ为介质磁导率，为磁性体的磁矩，r为磁性体至测点的位矢，

磁性体的磁场梯度张量[9-10]为：

磁场梯度张量的模量为：

磁场梯度张量的模量亦可表示为[11]：

k与磁性体至测点的距离r无关，仅与磁性体至测点的连线和磁偶极子的轴线的夹角相关。式(5)中，参数k近似为[12]：

式中，ϑ为磁性体至测点的连线与磁偶极子的轴线的夹角。当90°≤ϑ≤180°时，参数k的取值与0°≤ϑ≤90°对应的取值对称，以下kXY和kZ同理。

定义磁场梯度张量的局部模量为：

通过式(7)得到磁场梯度张量的局部模量，即磁场梯度张量局部缩并——将磁场梯度张量G中的部分梯度参数缩并为标量CX、CY、CZ、CXY、CXZ及CYZ。

磁场梯度张量的局部模量CX、CY、CZ、CXY、的表达式为：

式中，kX、kY、kZ、kXY、kXZ及kYZ为参数，其他参数的含义同式(5)，其中kXY、kXZ及kYZ可分别表示为：并且有

由于磁场梯度张量的局部模量CX、CY与磁矩、位矢r及ϑ相关（CXZ和CYZ同样），而磁场梯度张量的局部模量CZ和CXY仅与磁矩、距离及ϑ相关，若应用在磁场梯度张量定位中，则参量更少，使用更便捷，故本文后续仅研究磁场梯度张量的局部模量CZ和及相应的参数kZ和kXY。

2 基于磁偶极子的磁场梯度张量局部缩并的理论分析

由式(1)～(8)可得到CXY、kXY、CZ和kZ值的空间分布特征，见图1～4，其中kXY和kZ的部分取值见表1。和CZ与磁矩和距离相关，在计算CXY和CZ时，为便于显示其空间分布特征，取磁矩M=1.0 A·m2，

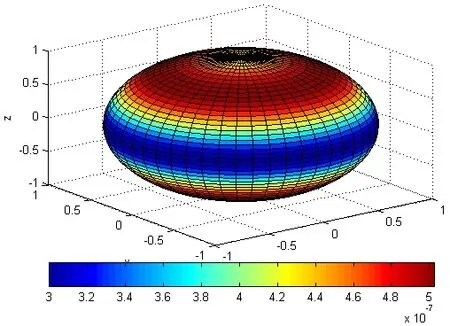
图1 CXY的空间分布Fig.1 Spatial distribution of parameter CXY

图2 kXY的空间分布Fig.2 Spatial distribution of parameter kXY

图3 CZ的空间分布Fig.3 Spatial distribution of parameter CZ

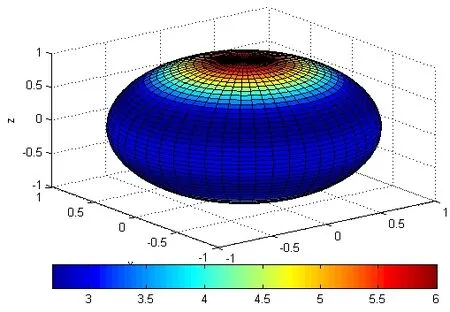
图4 kZ的空间分布Fig.4 Spatial distribution of parameter kZ

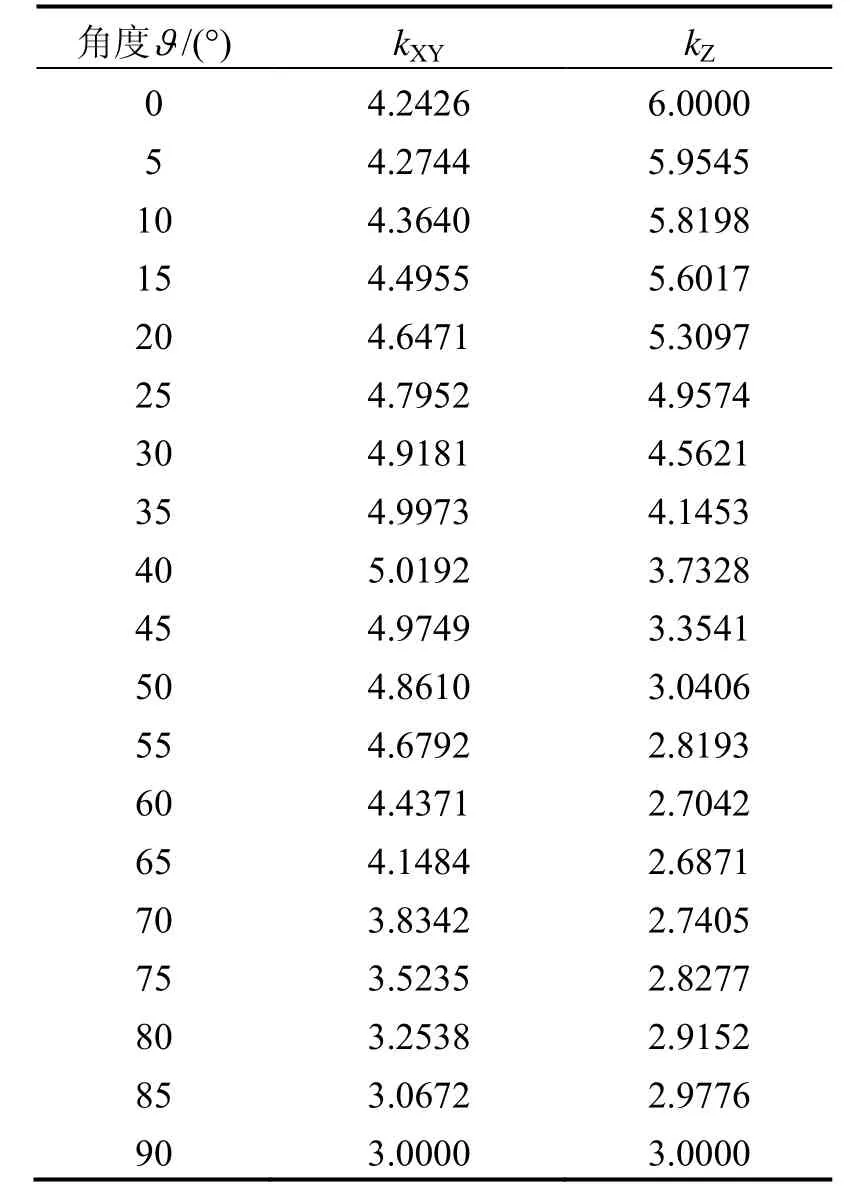
表1 kXY和kZ值的理论反演值Tab.1 Theoretical inversive value of kXY and kZ

由图1可得，对于相同距离r的测点（几何上为球体）：当0°≤ϑ≤90°时，CXY先增大后减小；在ϑ=39°时，CXY取最大值；在ϑ=90°（在与磁偶极子轴线正交的赤道）时，CXY取最小值。

由图 2可得，kXY值的空间分布规律与磁场梯度的局部模量CXY相同，但与距离r无关，仅与ϑ（磁性体至测点的连线与磁偶极子的轴线之间的夹角）相关。在ϑ=0°时，kXY为 4.2426；在ϑ=39°时，kXY取最大值5.0199；在ϑ=90°时，kXY取最小值3.0000。

由图3可得，对于相同距离r的测点（几何上为球体）：当0°≤ϑ≤90°时，CZ先减小后增大；在ϑ=0°（与磁偶极子轴线一致的极点）时，CZ取最大值；在ϑ=63°时，CZ取最小值。

由图4可得，kZ值的空间分布规律与磁场梯度的模量CZ相同，但与距离r无关，仅与ϑ相关。在ϑ=0°时，kZ取最大值 6.0000；在ϑ=63°时，kXY取最小值2.6836；在ϑ=90°时，kZ为 3.0000。

kXY、kZ与磁性体至测点的距离r无关，仅与磁性体至测点的连线和磁偶极子的轴线的夹角ϑ相关，此时，参数kXY和kZ为：

取ϑ=0°～90°，间隔为 1°，则样本为 91个，取显著性水平α=0.05，采用K-S假设检验复核上述拟合公式。当时，则样本符合假定的分布函数。对于式(9)，可见，kXY、kZ值与角度ϑ之间的关系符合拟合公式(9)和(10)的分布规律。

3 磁场梯度张量局部缩并的试验验证

通过4个三轴磁传感器（美国PNI公司生产）组成磁传感探头测量磁场梯度张量。采用基于电流脉冲的步进电机角度控制系统作为旋转试验平台。磁性体采用烧结钕铁硼永磁铁，为圆柱形，直径为8 mm，高8 mm，剩磁为1.23 T，矫顽力为860 kA/m，其磁矩约为0.048 A·m2。永磁铁的中心设为坐标原点O(0, 0, 0)，磁传感探头的坐标为(0, 0.2sinϑ, 0.2cosϑ )。通过旋转试验平台，磁传感探头可测量与永磁铁的磁偶极子轴线夹角在0°～90°范围的磁场梯度张量的局部模量CXY和CZ，进一步可得到kXY和kZ值。试验平台的实物见图5。

基于前述的式(1)～(10)可计算得到局部模量CXY、和参数kXY、kZ值，其与实测值的对比见图6～9。

由图6和图7可得，磁场梯度张量的局部模量CXY及kXY值随着ϑ先增大后减小，在ϑ=39°时取最大值，在ϑ=90°时取最小值，其与理论计算值基本一致。

由图8和图9可得，磁场梯度张量的局部模量CZ及值随着ϑ先减小后增大，在ϑ=63°时取最小值，在ϑ=0°时取最大值，其与理论计算值基本一致。可见，磁场梯度张量的局部模量CXY（或CZ）与kXY（或kZ）值的分布趋势相同，且试验结果与前述的理论分析中的空间分布特征一致。

图5 试验平台的实物图Fig.5 Photograph of experimental system

图6 kXY值的试验值与理论值的比较Fig.6 Comparison between experimental and theoretical values of kXY

图7 局部模量CXY的试验值与理论值的比较Fig.7 Comparison between experimental and theoretical values of CXY

图8 kZ值的试验值与理论值的比较Fig.8 Comparison between experimental and theoretical values of kZ

图9 局部模量CZ的试验值与理论值的比较Fig.9 Comparison between experimental and theoretical values of CZ

4 结 论

1）本文针对磁场梯度张量的实际测量中通常仅可测得部分磁场梯度张量元素的现状，为有效利用这些部分磁场梯度参数，考虑磁场梯度张量缩并理论的日益广泛的应用，发展了基于磁偶极子的磁场梯度张量局部缩并方法。

2）提出了磁场梯度张量局部缩并的方法，并给出了磁场梯度张量局部模量的概念。分析了局部模量及相关参数的空间分布规律，结果表明：局部模量CXY及kXY值随着ϑ先增大后减小，在ϑ=39°时取最大值，在ϑ=90°时取最小值；局部模量CZ及kZ值随着ϑ先减小后增大，在ϑ=63°时取最小值，在ϑ=0°时取最大值。

3）提出了局部模量计算中相关重要参数的近似计算公式，对磁场梯度张量的局部模量CXY、CZ及近似公式中kXY和kZ值与角度ϑ的关系进行了试验验证，其试验值与理论公式计算值基本一致。

4）由于磁场梯度张量在磁场定位理论中的重要性及部分磁场梯度传感器的发展，磁场梯度张量局部缩并理论值得进一步的研究。

（References）：

[1]Clark D A. New methods for interpretation of magnetic vector and gradient tensor data I: eigenvector analysis and the normalised source strength[J]. Exploration Geophysics, 2012, 43(4): 267-282.

[2]Clark D A. New methods for interpretation of magnetic vector and gradient tensor data II: application to the Mount Leyshon anomaly, Queensland, Australia[J]. Exploration Geophysics, 2013, 44(2): 114-127.

[3]Beiki M, Clark D A, Austin J R, et al. Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data[J]. Geophysics,2012, 77(6): J 23-J37.

[4]Sui Yang-yi, Li Guang, Wang Shi-long, et al. Asphericity errors correction of magnetic gradient tensor invariants method for magnetic dipole localization[J]. IEEE Transactions on Magnetics, 2012, 48(12): 4701-4706.

[5]吴志东, 周穗华, 陈志毅. 磁场梯度张量在磁性椭球体跟踪中的应用[J]. 华中科技大学学报(自然科学版),2013, 41(11): 103-107.Wu Zhi-dong, Zhou Sui-hua, Chen Zhi-yi. Application of magnetic gradiometer tensor to magnetic ellipsoid tracking[J]. Huangzhong University of Science & Technology(Natural Science Edition), 2013, 41(11): 103-107.

[6]刘欢, 董浩斌，葛健, 等. 基于Overhauser效应的磁场梯度探测器[J]. 仪器仪表学报, 2015, 36(3): 592-600.Liu Huan, Dong Hao-bin, Ge Jian, et al. Magnetic field gradient detector based on the nuclear Overhauser effect[J]. Chinese Journal of Scientific Instrument, 2015, 36(3):592-600.

[7]蹇兴亮, 周克印. 基于磁场梯度测量的磁记忆试验[J].机械工程学报, 2010, 46(4): 15-21.Jian Xing-liang, Zhou Ke-yin. Magnetic memory experiment based on magnetic gradient measurement[J]. Journal of Mechanical Engineering, 2010, 46(4): 15-21.

[8]张朝阳, 肖昌汉, 高俊吉, 等. 磁性物体磁偶极子模型适用性的试验研究[J]. 应用基础与工程科学学报,2010, 18(5): 862-868.Zhang Zhao-yang, Xiao Chang-han, Gao Jun-ji, et al.Experiment research of magnetic dipole model applicability for a magnetic object[J]. Journal of Basic Science and Engineering, 2010, 18(5): 862-868.

[9]Huang Yu, Wu Li-hua, Sun Feng. Underwater continuous localization based on magnetic dipole target using magnetic gradient tensor and draft depth[J]. IEEE Geoscience& Remote Sensing Letters, 2014, 11(11): 178-180.

[10]Yin Gang, Zhang Ying-tang, Fan Hong-bo, et al. Linear calibration method of magnetic gradient tensor system[J].Measurement, 2014, 56: 8-18.

[11]Wiegert R F, Oeschger J. Generalized magnetic gradient contraction based method for detection, localization and discrimination of underwater mines and unexploded ordnance[C]//Proceedings of MTS/IEEE. Washington, 2005:1325-1332.

[12]江胜华, 申宇, 褚玉程. 基于磁偶极子的磁场梯度张量缩并的试验验证及相关参数确定[J]. 中国惯性技术学报, 2015, 23(1): 103-106, 114.Jiang Sheng-hua, Shen Yu, Chu Yu-cheng. Experimental verification and related parameter’s determination for magnetic gradient tensor contraction using magnetic dipole[J]. Journal of Chinese Inertial Technology, 2015,23(1): 103-106, 114.

Theoretical study and experimental verification of magnetic gradient tensor partial contraction using magnetic dipole

JIANG Sheng-hua1,2, HOU Jian-guo3, HE Ying-ming3, WANG Shi-ji1
(1. College of Engineering and Technology, Southwest University, Chongqing 400715, China;2. School of Civil and Environmental Engineering, Nanyang Technological University, 639798, Singapore;3. School of Civil Engineering, Wuhan University, Wuhan 400712, China)

The magnetic gradient tensor contraction theory can effectively describe a magnetic source without being influenced by the orientation of magnetic measuring instrument. However, in the actual measurement of magnetic field gradient tensor, only a part of gradient parameters can usually be obtained due to some hardly inevitable factors. To effectively use these parameters, a magnetic gradient tensor partial contraction method is put forward based on magnetic dipole theory, and the conception of magnetic gradient tensor’s partial modulus is given. The three-dimensional distribution of magnetic gradient tensor’s partial modulus and related parameters is analyzed, and the theoretical formulae of the related parameters are derived. The verification experiments show that the partial modulusCXYand the parameterkXYincreases with ϑ ranged from 0° to 39°,and decreases with ϑ ranged from 39° to 90°. TheCXYandkXYare maximum when ϑ is 39°, and are minimum when ϑ is 90°. The partial modulusCZand parameterkZdecreases with ϑ ranged from 0° to 63°, and increases with ϑ ranged from 63° to 90°. TheCZandkZare maximum when ϑ is 0°, and are minimum when ϑ is 63°.These experimental values are in accordance with the theoretically calculated values, showing that the proposed method can provide reference for the application of the magnetic gradient tensor contraction theory.

magnetic dipole; magnetic gradient tensor; partial contraction; partial modulus

1005-6734(2017)04-0473-05

10.13695/j.cnki.12-1222/o3.2017.04.009

TM153

A

2017-04-10；

2017-07-25

国家自然科学基金（51208078）；重庆市前沿与应用基础研究计划（cstc2015jcyjA30008）；中央高校基本科研业务费专项资金（XDJK 2015B007）

江胜华（1982—），男，工学博士，博士后，副教授，主要从事基于磁场的结构健康监测等方面的研究。E-mail: jiangsh@whu.edu.cn