串件拼修对策下K/N(G)结构系统可用度评估建模
2017-11-17周亮李庆民彭英武李华
周亮, 李庆民, 彭英武, 李华
1.海军工程大学 兵器工程系, 武汉 430033
2.海军工程大学 科研部, 武汉 430033
串件拼修对策下K/N(G)结构系统可用度评估建模
周亮1, 李庆民2,*, 彭英武1, 李华1
1.海军工程大学 兵器工程系, 武汉 430033
2.海军工程大学 科研部, 武汉 430033
针对作战编队自主保障期间,作战单元对装备故障仅具备换件修理、保障单元对备件修复概率小于1的保障特点,扩展备件管理多级(METRIC)模型,建立了装备冗余和外场更换件(Line Replaceable Unit,LRU)冗余结构下非串件策略和串件策略两级单层备件库存保障模型。以备件贮存空间为约束,可用度为目标,对非串件策略系统建立有限解空间下的分层边际优化模型。依据备件保障流程,基于蒙特卡罗仿真方法建立了两级维修保障仿真模型。实例分析结果表明:当系统可用度较低,采用串件策略能极大提高系统可用度;仿真结果与解析结果一致,本文建模方法正确。模型可为保障决策者制定编队随行备件方案提供参考。
自主保障; 备件管理多级(METRIC); 串件; 有限解空间; 边际; 蒙特卡罗仿真
作战编队通常由一个保障单元和多个作战单元组成,备件是编队最重要的保障资源之一。为了提高装备可靠性,装备设计者对装备结构常进行冗余设计,而为了提高任务成功率,装备亦会出现冗余情况,一旦有装备出现故障,冗余装备将启动开始工作。而在外独立执行任务的作战编队,由于编队修理能力限制,作战单元通常只有拆换件修理能力,保障单元对拆换下来的故障件有一定的修理能力,仅可修复部分故障件,因此不可修的备件随时间越来越多,随行库存备件随时间越来越少。随着装备的发展,电子装备越来越集成化和模块化,抽取和拆换部件操作方便,使故障件尽可能集中在少的装备上变得简单易行。对于携带备件能力有限的作战编队,当装备发生故障,仓库备件消耗殆尽时,从其他同型装备拆卸部件来换修另一台装备上的故障件,使故障件尽量集中在最少的装备上,这是提高装备可用度的有效手段。如由4部相控阵雷达构成的跟踪系统,天线元件采用冗余设计,执行任务期间要求相控阵雷达的最小工作数为3部,当备件消耗殆尽时,可以将失效的天线元件尽可能集中在一部相控阵雷达上,以此提高跟踪系统的可用度。由于任务期间备件修复概率小于1,保障系统备件处于非稳态需求,不适合采用传统的生灭过程模型和备件管理多级(METRIC)模型进行计算,因此研究任务期间冗余系统在串件拼修策略下的备件库存模型,对提高装备完好性具有重要意义。
目前,国内外有大量文献对备件库存问题做了研究。对备件完全可修复条件下系统备件处于稳态需求时的可用度模型有:文献[1-5]研究并建立了多级保障结构、维修渠道有限、横向转运、K/N统批量维修等可修复系统备件库存控制模型;文献[6-7]考虑了串件拼修和不完全串件拼修对装备可用度的影响;文献[8]考虑了备件送修、库存分配先后顺序及串件拼修策略对系统可用度的影响。但均不适合计算备件修复概率小于1时保障系统的备件库存方案。对保障系统时变可用度模型的研究有:文献[9-10]基于动态帕尔母定理,分别建立了两级和三级备件保障结构下系统时变可用度模型;文献[11]利用非平稳随机过程理论,在考虑维修渠道数量有限情况下,建立了两级单层可修复系统时变可用度模型;文献[12]对备件修复概率小于1的保障系统,将不全修复件等效为消耗件,建立了多层级不完全修复件近似可用度评估模型。但均未考虑串件拼修对装备完备性的影响。
本文针对作战编队自主保障期间的保障特点,考虑作战单元装备冗余和外场更换件(Line Replaceable Unit,LRU)冗余对装备系统完好性的影响,采用理论建模与仿真实验相结合的方法,建立作战编队备件库存保障模型,对作战编队串件策略前后系统可用度变化进行研究。
1 条件假设及变量说明
1.1 条件假设
1) LRU寿命服从指数分布。
2) 装备停机仅由一项部件故障造成,忽略换件维修时间。
3) 不考虑备件在不同装备使用现场间的横向供应。
4) 使用现场库存实行(s-1,s)策略,即作战单元向保障单元送修一项故障件,同时向保障单元申领相同数量的备件。
5) 作战单元仅对故障件有更换维修能力,保障单元对故障件修复概率小于1,且实行先到先修。
1.2 变量说明
变量说明如下:H0为保障单元,保障所有的作战单元;Combat为所有作战单元的集合;Part为装备中所有类LRU组成的集合;j为第j个作战单元,j∈Combat;l表示第l类LRU,l=1,2,…,n,l∈Part。
2 修复概率小于1时备件供应渠道建模
2.1 装备钝化条件下需求计算
装备在工作的过程中,若装备工作的强度不变,则其对备件需求亦不变,当装备出现故障停机时,发生故障的装备不再产生需求,称之为装备钝化。因此t时刻第j个作战单元在单位时间内LRU的需求为[9]
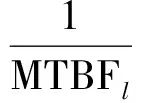
(1)
式中:Kz为作战单元j中装备z的最小工作数;M为 LRU在装备z中的单机安装数;Ac(t-1)为系统在t-1时刻的可用度;MTBFl为LRU的平均故障间隔时间。
2.2 备件供应渠道数概率分布
编队作战期间,由于作战单元j对装备一般仅有拆换部件的能力,拆换下来的备件送保障单元H0修理,同时向保障单元申领同样数量的备件。设保障单元H0对LRU的修复概率为r,修理LRU平均所需的时间为τl,不能修复的故障件等到任务结束后送基地修理。若任务时刻t小于LRU平均修理时间τl,则t时刻保障单元H0在修数量为:0~t时间内各作战单元产生的故障件之和与保障单元H0对LRU修复概率之乘积;若τl≤t,则t时刻保障单元H0的在修数量为:t-τl~t时间内各作战单元产生的故障件之和与保障单元H0对LRU修复概率之乘积[13]。而t时刻,保障单元H0中LRU供应渠道由在修数量和不可修数量两部分构成,因此保障单元H0中LRU供应渠道的均值为
X0l(t)=
(2)
X0l(t)服从均值和方差相同的泊松分布,因此t时刻保障单元H0中LRU供应渠道数为x的概率为
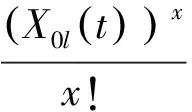
(3)
故t时刻保障单元H0中LRU的期望短缺数和期望方差为
(4)
式中:S0l为保障单元H0中LRU的库存数量。
由于作战单元j仅有拆换修理能力,拆换下来的故障件将送往保障单元H0进行修理,同时向保障单元申领相同数量的备件。由于保障单元H0库存能力有限,且修复概率小于1,随着时间推进,备件库存量将会越来越少,不能满足作战单元j的备件需求,将产生保障延误。
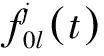
(5)
t时刻作战单元j的供应渠道由两部分构成:一是保障单元H0在t-ost时刻备件短缺造成作战单元j保障延误的数量,ost为作战单元j到保障单元H0的运输时间;二是保障单元H0对作战单元j补给途中的部分。因此,t时刻作战单元j中LRU供应渠道均值为
(6)
方差为
(7)
由文献[13]可知,t时刻当作战单元j中LRU的供应渠道差均比大于1时,LRU的供应渠道服从Γ(a,b)的负二项分布,分布参数(a,b)为
(8)
t时刻当作战单元j中LRU的供应渠道差均比小于1时,LRU的供应渠道服从η(p,n)的二项分布[13],分布参数(p,n)为
(9)
t时刻当作战单元j中LRU的供应渠道差均比等于1时,LRU的供应渠道服从均值为E[Xjl(t)]的泊松分布[13]。
因此,根据t时刻作战单元j中LRU的供应渠道差均比与1的大小,由式(3)、式(8)和式(9)可确定LRU供应渠道数的概率分布,进而得到LRU备件数量为Sjl时,备件短缺数为α的概率分布P(BOjl(Sjl,t)=α),BO为备件短缺数分布概率。
3 串件策略下K/N(G)可用度模型
3.1 非串件系统可用度模型
不考虑系统串件拼修时,停机装备中好的部件不能拆卸到其他因该部件损坏而停机的装备上使用。求取系统在t时刻的可用度Ac(t)可分为两步:第1步先通过超几何分布求取系统中一部装备z在t时刻的可用度Az(t);第2步根据二项分布求取系统中要求Kz部装备完好的概率。系统下有z型装备Nz部,每部z型装备中只有M个LRU,因此系统中LRU有NzM个。当系统LRU总短缺数为x时,若装备下LRU短缺数为u,则剩下的x-u件LRU分布在剩下的Nz-1部装备当中,因此一部z型装备中LRU短缺μ个的概率φzl(μ,x,t)为
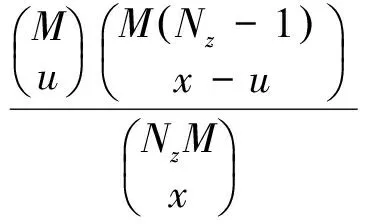
(10)
P(BOjl(Sjl,t1)=x))dt1
(11)
装备z中不同类型的LRU均处于串件关系,因此,t时刻装备z的可用度Az(t)为[12]
(12)
一部装备在t时刻的可用度为Az(t),则Nz部装备中有y部完好的概率为
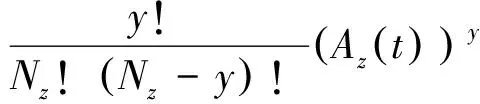
(13)
由于未考虑预防维修及装备故障换件维修时间,因此装备供应可用度与使用可用度相同,依据文献[15]中K/N(G)供应可用度的求取方法,由Nz部装备构成的系统可用度近似为
(14)
3.2 串件系统可用度模型
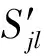
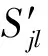
(15)
因此,t时刻作战单元j中装备在z的期望停机数为
EBZ(t)=0+1(D(1,t)-D(0,t))+
2(D(2,t)-D(1,t))+…+
y(D(y,t)-D(y-1,t))+…
y≤Kz
(16)
t时刻作战单元j中装备在z构成的系统可用度为
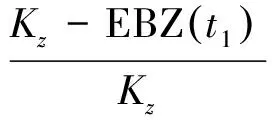
(17)
4 有限解空间分层边际优化模型及步骤
4.1 目标函数和约束条件
在制定备件方案时,决策层更看重每次任务的完成效果,要求装备有较高的完好性。而受贮存空间限制,备件携带数量有限,在系统可用度达到目标可用度前提下,要求备件贮存所需的体积最小,因此边际优化目标函数和约束条件为
(18)
式中:Ac0为系统c的目标可用度;vl为备件LRU的体积。
4.2 有限解空间分层边际算法优化步骤
边际算法广泛用于VMETRIC和OPUS等库存优化配置软件中。传统的边际算法是比较每项备件每增加一个时增加的边际效益值,对边际效益值最大的备件项目加1,其他备件项目数量保持原有状态,直到可用度大于等于目标可用度时算法结束[13]。因此,在确定备件方案的过程中,需要重复计算备件项目增加一个时的效益值,导致优化效率较低,通过将系统可用度分解到每项LRU,确定每项LRU备件配置数量范围后,对效益值最大的备件项目数加1,直至系统可用度大于目标可用度,其优化步骤如下:
1) 根据系统目标可用度wc,通过二分法求解装备可用度Az。
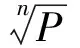
3) 确定目标可用度值下的最优备件方案。各项备件不同数量(m>0)下对应的效益值如矩阵Δp所示。设第k项备件配置数量为x的效益值为Δpkx,确定初始效益值矩阵
[Δp11Δp21… Δpj1]
对效益值最大的站点备件项目数量加1,计算此时系统可用度Ac。
4) 若Ac 4.3 复杂度分析 与传统的边际算法相比,若达到目标可用度需迭代s次,对于j个站点,L类备件,传统的边际优化算法复杂度为sjL,而有限空间解条件下的分层边际优化算法复杂度约为s+jL,优化效率高于传统的边际算法效率。 根据装备结构、备件保障及修理模型,采用蒙特卡罗仿真方法模拟装备实际保障过程,采用统计学方法对装备故障时间、维修时间、停机时间进行统计,从而得到系统的可用度[16]。仿真模型分为3部分:备件入库事件、故障件修理事件和换件维修事件。对于非串件系统,一旦运行中的装备发生故障,如果导致装备停机故障部件的备件库存大于0,则立刻用备件更换故障件;若库存小于0,则立即启动备份的装备。因此,冗余装备相当于“万能备件”,任何故障导致装备停机,冗余装备都能顶上,保证系统的正常运行,其仿真流程如图1 所示。 假设由3个相同的作战单元 (J1,J2,J3)和1个保障单元(H0)组成的编队,外出执行任务,任务时间为2 000 h。以作战单元中由2部相控阵雷达构成的目标跟踪系统为例,跟踪系统中相控阵雷达在任务期间冗余度为1,备件保障信息清单如表1所示。不考虑串件拼修策略时,采用有限解空间分层边际算法对目标跟踪系统可用度为0.60、0.70、0.80、0.95时的备件方案进行优化,优化结果如表2所示。 采用串件策略模型和仿真实验对表2中备件方案进行评估和验证,结果如表3所示。分析表3 中数据,无论是串件策略模型,还是非串件策略模型,其解析结果与仿真实验结果基本一致,解析模型与仿真模型的绝对误差值均在3%以内,因此串件策略模型和非串件策略模型建模正确。当备件配置数量分别为方案Ⅰ、方案Ⅱ、方案Ⅲ时,串件策略下目标跟踪系统可用度较非串件策略下系统可用度分别提高了约20%、15%、10%。在备件方案Ⅳ,串件策略下系统可用度值比非串件策略下系统可用度值略高,这是因为在高可用度下,可用度随着备件数量的增加呈现扁平化趋势,因此,即使采取串件拼修策略,系统可用度效果提高不明显。 如若将任务时间延长至5 000 h,备件方案Ⅰ和方案Ⅳ下系统可用度随时间变化如图3所示。在备件方案Ⅰ下,串件系统可用度与非串件系统可用度的差值随时间先变大,后变小;而在备件方案Ⅳ下,在2 000 h前,串件系统可用度与非串件系统可用度基本相同,随着任务时间的变长,串件系统可用度与非串件系统可用度差值慢慢增大,因此在任务时间小于2 000 h前,不用采取串件拼修策略,而在2 000 h后采取串件维修策略。 图1 仿真流程5 蒙特卡罗仿真建模
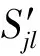
6 案例分析
Fig.1 Simulation flow
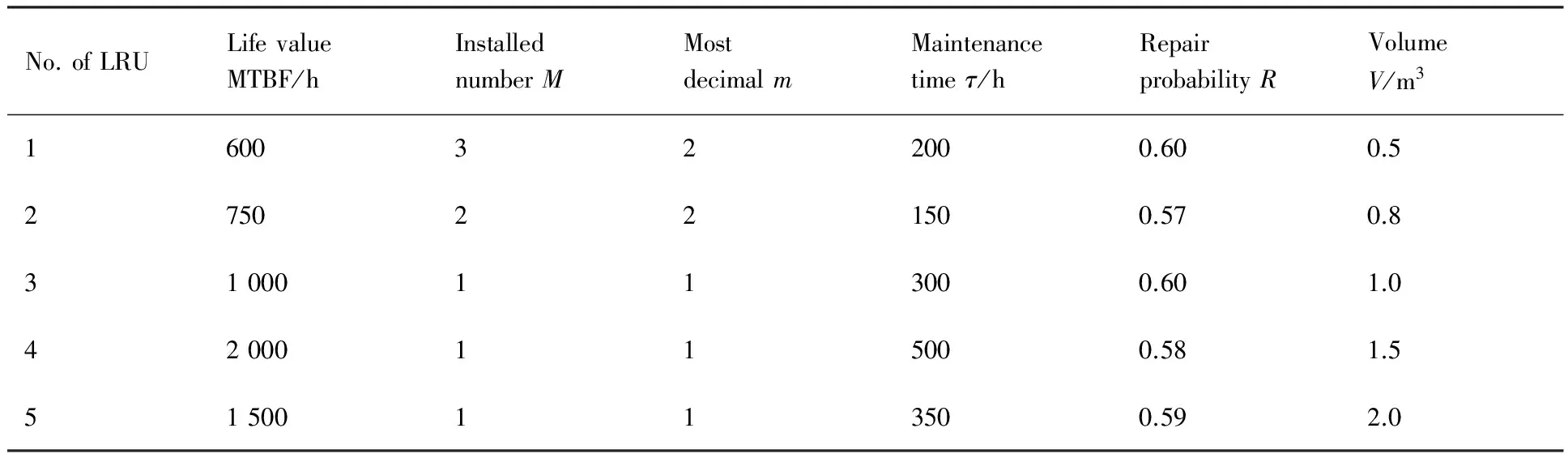
表1 备件保障信息清单Table 1 Lists of spare parts and parameters
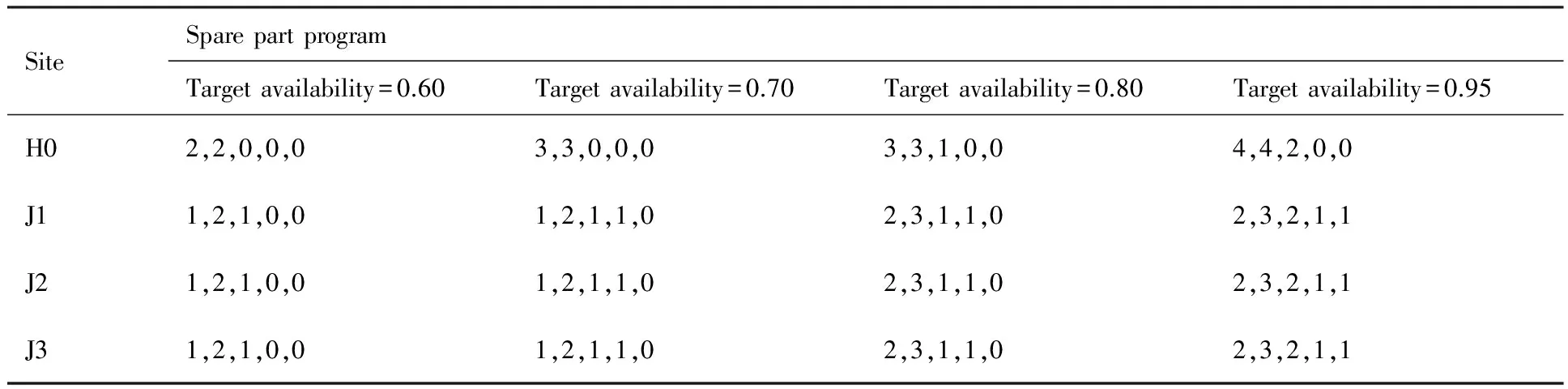
表2 不同目标可用度下的备件方案Table 2 Spare part programs for different target availabilities
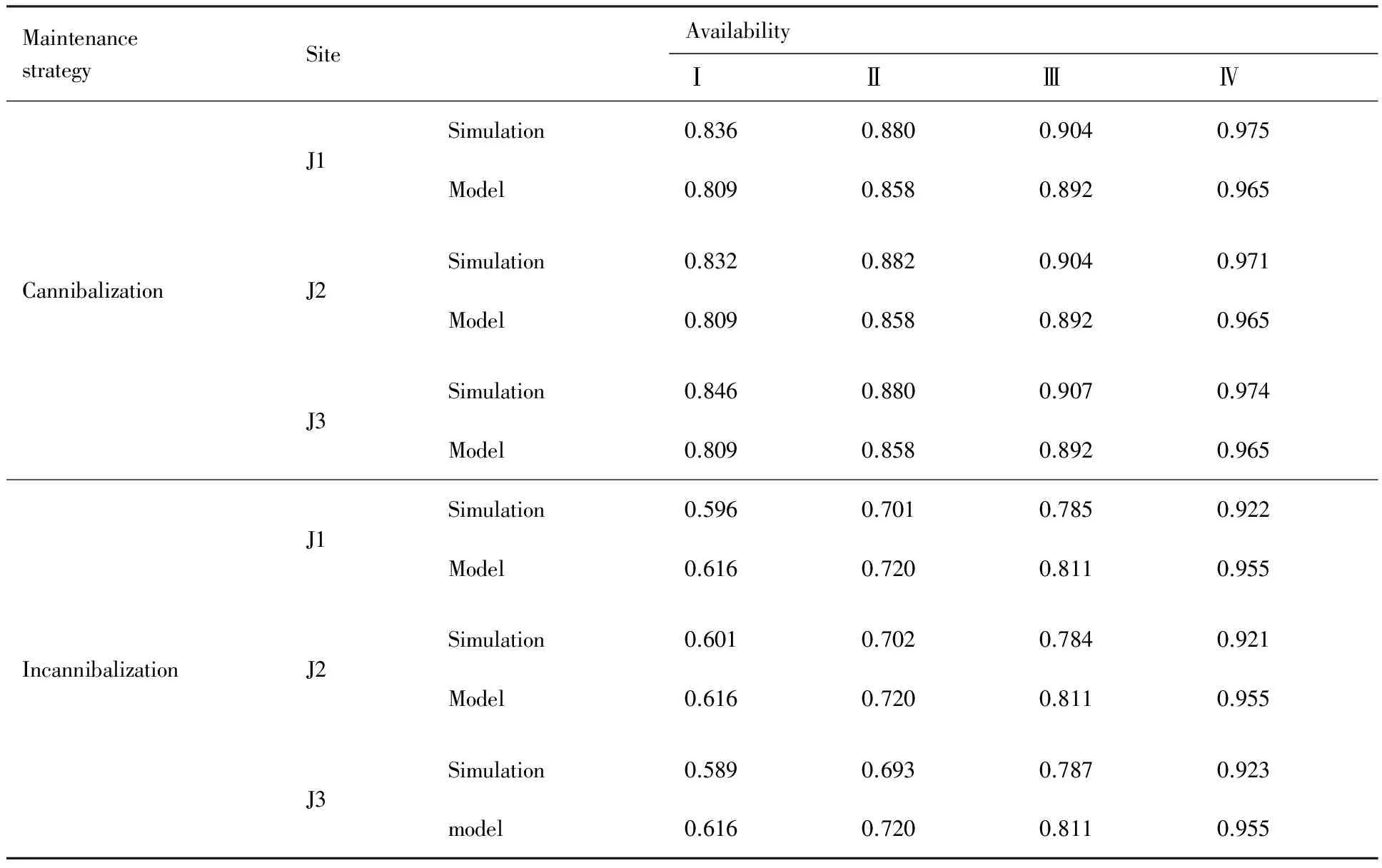
表3 不同备件方案下串件与非串件策略的可用度值Table 3 Availabilities of cannibalization and non-cannibalization for different spare part programs
图2 串件策略系统换件维修事件仿真流程
Fig.2 Simulation flow of replacement maintenance event for systems with cannibalization
图3 可用度随时间变化
Fig.3 Changes of availabilities with time
7 结 论
1) 在系统可用度较低的备件方案下,串件策略能大幅提高系统的可用度。
2) 在系统可用度较高的备件方案下,串件策略对系统可用度提高不明显。
3) 对已经制定好的备件方案,可以采用本文模型对备件方案进行评估,以帮助决策者是否选择串件拼修策略及串件拼修策略时机。
随着任务时间的延长,系统的可用度会不断降低,而作战编队可提供贮存备件的空间有限,因此要保证系统的可用度,需要进行中途补给。
[1] 张光宇, 李庆民, 李华. 零备件的多点库存单向转运模型与算法[J]. 航空学报, 2013, 34(5): 1092-1100.
ZHANG G Y, LI Q M, LI H. Modeling of unidirectional lateral transshipment in multi-location inventory systems[J] . Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1092-1100 (in Chinese).
[2] 徐立, 李庆民, 李华. 考虑多类维修优先权的多级维修供应系统库存控制[J]. 航空学报, 2015, 36(4): 1185-1194.
XU L, LI Q M, LI H. Inventory control of multi-echelon maintenance supply systems with multiple repair priorities[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1185-1194 (in Chinese).
[3] AHMAD H, MATTHIEU H. Interval availability analysis of a two-echelon multi-item system[J]. European Journal of Operational Research, 2013(228): 494-503.
[4] 张永强, 徐宗昌, 呼凯凯, 等.k/n系统维修实际与备件携行量联合优化[J]. 北京航空航天大学学报, 2016, 42(10): 2190-2197.
ZHANG Y Q, XU Z C, HU K K, et al. Joint optimization of maintenance time and carrying spare partsfork-out-of-nsystem[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(10): 2190-2197 (in Chinese).
[5] 薛陶, 冯蕴雯, 秦强. 考虑报废的K/N冷备份冗余系统可修复备件优化[J]. 华南理工大学学报 (自然科学版), 2014, 42(1): 41-46.
XUE T, FENG Y W, QIN Q. Optimization of repairable spare parts forK/Ncold-standby redundant system considering scraps[J]. Journal of South China University of Technology (Natural Science Edition), 2014, 42(1): 41-46 (in Chinese).
[6] 阮旻智, 李庆民, 彭英武, 等. 串件拼修对策下多级维修供应的装备系统可用度评估[J]. 航空学报, 2012, 33(4): 658-665.
RUAN M Z, LI Q M, PENG Y W, et al. Evaluation of equipment system availability for multi-echelon maintenance supply with cannibalization[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(4): 658-665 (in Chinese).
[7] SALMAN S, CASSADY C R, POHL E A, et al. Evaluating the impace of cannibalization on the fleet performance[J]. Quality and Reliability Engineering International, 2007, 24(4): 445-457.
[8] 王慎, 李庆民, 彭英武, 等. 串件拼修对策下两级备件维修供应系统动态管理模型[J]. 航空学报, 2013, 34(6): 1326-1335.
WANG S, LI Q M, PENG Y W, et al. Dynamic management model of two-echelon maintenance supply system for spare parts with cannibalization[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1326-1335 (in Chinese).
[9] LAU H C, SONG H, SEE T C, et al. Evaluation of time-varying availability in multi echelon spare parts systems with passivation[J]. European Journal of Operational Research, 2006, 170(1): 91-105.
[10] 王睿, 雷红伟, 彭英武, 等. 战时任务条件下舰艇装备多级备件优化[J]. 上海交通大学学报, 2013, 47(4): 398-403.
WANG R, LEI H W, PENG Y W, et al. Optimal of warship spare parts in the scenario of wartime mission[J]. Journal of Shanghai Jiaotong University, 2013, 47(4): 398-403 (in Chinese).
[11] 刘勇, 武昌, 李阳, 等. 两级备件保障系统的装备时变可用度评估模型[J]. 兵工学报, 2010, 31(2): 253-256.
LIU Y, WU C, LI Y, et al. Evaluation model of equipment time varying availability in two echelon spare support system[J]. Acta Armamentarii, 2010, 31(2): 253-256 (in Chinese).
[12] 李华, 李庆民, 刘任洋, 等. 任务期内多层级不完全修复件的可用度评估[J]. 系统工程与电子技术, 2016, 38(2): 476-480.
LI H, LI Q M, LIU R Y, et al. Evualtion of availability for multi-indenture partial repairable spares during the mission[J]. Systems Engineering and Electronics, 2016, 38(2): 476-480 (in Chinese).
[13] SHERBROOKE C C. Optimal inventory modeling of systems: Multi-echelon techniques[M]. 2nd ed. Boston: Artech House, 2004: 29-31.
[14] 张志华. 可靠性理论及工程应用[M]. 北京: 科学出版社, 2012: 5-10.
ZHANG Z H. Reliability theory and engineering application[M]. Beijing: Science Press, 2012: 5-10 (in Chinese).
[15] 卢雷, 杨江平.K/N(G)结构系统初始备件配置方法[J]. 航空学报, 2014, 35(3): 773-779.
LU L, YANG J P. Initial spare allocation method forK/N(G) structure system[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 773-778 (in Chinese).
[16] 任敏, 陈全庆, 沈震. 备件供应学[M]. 北京: 国防工业出版社, 2013: 278-289.
REN M, CHEN Q Q, SHEN Z. Spare parts supply[M]. Beijing: National Defense Industry Press, 2013: 278-289 (in Chinese).
AvailabilityevaluationmodelingforK/N(G)structuresystemwithcannibalization
ZHOULiang1,LIQingmin2,*,PENGYingwu1,LIHua1
1.DepartmentofWeaponryEngineering,NavalUniversityofEngineering,Wuhan430033,China2.OfficeofResearch&Development,NavalUniversityofEngineering,Wuhan430033,China
Duringthetaskofthecombatformationinindependentsupport,thecombatunitonlyhastheabilitytochangethefailedpartsofequipment,andthereparabilityprobabilityofsparepartsbythesupplyunitislessthan1.Byextendingthemulti-echelontechniqueforrecoverableitemcontrol(METRIC)model,thispaperestablishesamodelforsparepartinventorycontrolwithnon-cannibalizationandcannibalizationstrategiesforredundantequipmentandlinereplaceableunit(LRU)redundantstructuresystem.Themodeltakesthestoragespaceofsparepartsastheconstraint,andthesystemavailabilityasthetarget.Ahierarchicalmarginaloptimizationmodelisestablishedforthefinitesolutionspaceofthenon-cannibalizationstrategysystem.Onthebasisofsparepartssupportprocess,two-levelmaintenancesupportsimulationmodelisestablishedbasedonMonteCarlosimulationmethod.Theanalysisresultsoftheexampleshowthatthesystemavailabilitycanbegreatlyimprovedbyusingcannibalizationstrategy,andthesimulationresultsareconsistentwiththeanalyticalresults.Themodelcanprovidereferencefordecisionmakerstomaketheplanfortheformationoftheaccompanyingspareparts.
independentsupport;multi-echelontechniqueforrecoverableitemcontrol(METRIC);cannibalization;finitesolutionspace;marginal;MonteCarlosimulation
2016-04-14;Revised2016-04-19;Accepted2016-05-23;Publishedonline2016-06-301336
URL:www.cnki.net/kcms/detail/11.1929.V.20160630.1336.002.html
s:NationalDefencePre-researchFoundation(51327020105,51304010206)
2016-04-14;退修日期2016-04-19;录用日期2016-05-23; < class="emphasis_bold">网络出版时间
时间:2016-06-301336
www.cnki.net/kcms/detail/11.1929.V.20160630.1336.002.html
国防预研项目 (51327020105,51304010206)
*
.E-maillicheng001@hotmail.com
周亮, 李庆民, 彭英武, 等. 串件拼修对策下K/N(G)结构系统可用度评估建模J. 航空学报,2017,38(4):220319.ZHOUL,LIQM,PENGYW,etal.AvailabilityevaluationmodelingforK/N(G)structuresystemwithcannibalizationJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):220319.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0190
V125.7; E917; TJ07
A
1000-6893(2017)04-220319-10
(责任编辑: 苏磊)
*Correspondingauthor.E-maillicheng001@hotmail.com
