基于太阳能飞机应用的低雷诺数翼型研究

刘晓春， 祝小平， 周洲1,,*， 王科雷1,

1.西北工业大学 航空学院， 西安 710072

2.西北工业大学 无人机特种技术重点实验室， 西安 710065

基于太阳能飞机应用的低雷诺数翼型研究

刘晓春1, 2， 祝小平2， 周洲1,2,*， 王科雷1,2

1.西北工业大学 航空学院， 西安 710072

2.西北工业大学 无人机特种技术重点实验室， 西安 710065

以太阳能飞机为背景，对低雷诺数翼型FX 63-137进行了折线型建模以拟合典型晶硅太阳能电池片对气动外形的影响，开展了气动数值模拟分析。首先引用“拟合优度”的定义描述本文折线型翼型轮廓与基准翼型(Baseline)的吻合度，并以此参数为变量建立5种折线型翼型模型；然后，采用计算流体力学(CFD)方法计算分析了不同雷诺数下各折线型翼型的气动特性，并着重研究了低雷诺数下折线型翼型的绕流机理；最后，基于工程应用实际的需求，提出了晶硅太阳能电池片的铺设方法也即折线型翼型设计思想准则，并进行算例验证。研究结果表明：低雷诺数条件下，折线型翼型升阻性能相比光滑翼型在一定程度上表现出了优势，但随着雷诺数的增加，升阻方面的优势逐渐消失；折线型翼型压力分布受各折线段长度影响，前缘吸力峰值、压力平台范围以及压力恢复区分布特征是决定折线型翼型气动性能的主要因素；通过设计的算例验证了本文提出的折线型翼型设计思想的可行性。

太阳能飞机； 工程应用； 折线型翼型； 拟合优度； 低雷诺数； 气动性能

太阳能飞机具有高空超长航时的能力，在预警侦察、持久监视、数据中继等领域有着广阔的应用前景[1-2]。但太阳能飞机飞行高度高，速度低，飞行雷诺数低，如美国的“Helios”以及英国“Zephyr”[3-4]太阳能飞机，飞行雷诺数均处在几十万量级，低雷诺数问题[5-8]十分突出。

太阳能飞机不同于常规飞机，依靠太阳辐射为能源，需在机翼表面安装太阳能电池片。而为了不破坏机翼曲面外形，要求太阳能电池具有柔性[9]。目前，柔性太阳能电池效率低、价格昂贵，所以单晶硅电池依旧是太阳能飞机的主要选择。单晶硅电池一般以玻璃为衬底，所以不可弯曲。而为了达到赋形要求，一般采用小片单晶硅电池连成组件，近似成曲面，使得翼型上表面曲线型面变为多段折线型，对翼型气动特性也将造成影响[10]。因此，对低雷诺数条件下折线型翼型气动特性进行数值模拟研究具有较大的工程意义。

目前，对于不规则形状翼型问题的研究多从仿生或工程问题演化而来。如NASA Langley研究中心的Walsh[11-12]发现顺流向的微小肋条表面结构能有效降低摩擦阻力，突破了表面越光滑阻力越小的传统思维；Choi等[13]对高尔夫球进行了实验研究，发现小凹坑能够诱发层流剪切层不稳定，使局部分离气流有足够的能量重新附着在球体表面，具有较强的克服逆压梯度的能力，分离推迟，阻力减小；Beierle等[14]针对翼型表面突起物对压力分布的影响进行了数值模拟研究，发现随着向突起物逼近，压力逐渐上升，到达突起物时达到峰值，类似驻点流动，而突起物后方突然膨胀，压力相应减小。在国内，方洪等[15]对风洞试验中翼面测压孔附近几种不同形式毛刺对压力分布的影响进行了分析；张骏等[16]对风力机叶片二维与三维表面粗糙度效应进行了数值模拟研究。但是，目前有关晶硅太阳能电池片实际工程应用带来的折线型翼型表面问题的研究仍较少，呼文韬[17]粗略地考虑了太阳能飞机铺设太阳能电池对翼型气动性能的影响，但是假设了原翼型为最优翼型，仅仅考虑了电池布片率和翼型外形吻合度因素，对太阳能电池的尺寸进行了优化设计，并未对这种特殊的折线型翼型气动特性进行分析，因此很有必要对折线型翼型的低雷诺数气动特性进行更为细致的研究。

本文基于太阳能飞机工程研制的实际问题，对折线型翼型在低雷诺数条件下的气动特性以及折线型翼型的设计思想准则进行了研究。主要研究内容包括：考虑工程可能应用的几种尺寸的太阳能电池片，建立不同拟合优度折线型翼型模型；分析雷诺数、拟合优度对折线型翼型气动性能的影响；对低雷诺数下折线段对翼型绕流的影响机理进行深入研究；总结折线型翼型的设计思想准则，并通过设计算例加以验证。

1 计算方法与模型

1.1 湍流模型

γ输运方程为

(1)

(2)

与SST湍流模型耦合的方程为

(3)

式中相关变量所代表的意义及相关参数的具体值可参考文献[18-19]。

1.2 几何建模与数值方法

太阳能飞机主要在机翼上表面铺设太阳能电池片，更高的铺设面积利用率将意味着能够获得更多的的能量，但是由于机翼前缘曲率较大，以及后缘厚度较小，机翼的前后缘一般不作为太阳能电池片铺设使用，如“Helios”亦是如此(如图1(a)所示)。由于晶硅太阳能电池一般不具备柔性，使得太阳能飞机机翼剖面翼型在铺设太阳能电池范围内呈现出明显的折线型轮廓(如图1(b)所示)，这势必将对其气动性能造成影响。

参考上述实例特征，并依据SunSailor 2[20]太阳能无人机机翼铺设太阳能电池片面积占机翼总面积的81%，本文以FX 63-137低雷诺数翼型为基准翼型(Baseline)，以内接多边形的方式在翼型上表面0.1～0.9倍弦长范围内铺设5种不同尺寸的太阳能电池片，对应地建立5种折线型翼型模型，并使用非线性回归方程的拟合优度概念来表征各折线型翼型与基准翼型之间的吻合度。

图1 “Helios”太阳能无人机
Fig.1 “Helios” solar-powered unmanned aerial vehicle

将基准翼型轮廓曲线在铺设太阳能电池范围内按电池弦向尺寸划分为若干弧段，电池尺寸L视为预测值，弧长视为真实值，则拟合优度计算公式为

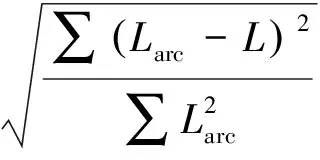
(4)

式中：R为拟合优度，R∈[0,1]，R越接近1，说明吻合度越高，与基准翼型越接近；Larc为每个折线段对应弧段的真实弧长。

表1给出了本文所建立的5种折线型翼型及其对应的拟合优度。基准翼型弦长为1 000 mm。可以看到，随着单片电池长度增大，拟合优度逐级递减。而为了描述方便，下文以主要使用的太阳能电池单片长度代表相对应的折线型翼型。

图2给出了Baseline以及折线型“200”翼型网格示意。计算采用C型结构网格，翼型远场取30倍弦长作为计算域边界，网格密度为528×114(流向×法向)，壁面第1层网格高度为2×10-5倍弦长，对翼型前后缘以及折线段转折处进行网格局部加密。

采用1.1节所介绍的基于SST模型的γ-Reθt转捩模型，数值求解采用有限体积法求解非定常可压缩Navier-Stokes方程。采用二阶精度Roe迎风格式离散对流项，黏性通量项采用中心差分格式离散，时间推进采用隐式LU-SGS (Lower-Upper Symmetric Gauss-Seidel)方法。本文计算时，子迭代步数取20步，物理时间步长取0.000 3。

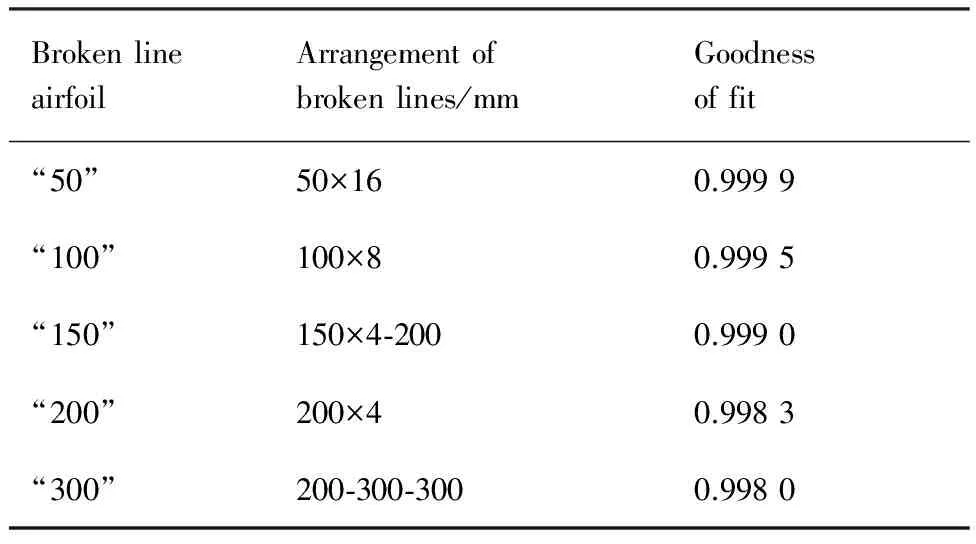
表1 不同折线型翼型对应的拟合优度Table 1 Goodness of fit of different broken line airfoils

图2 翼型近壁面网格
Fig.2 Closeup of grid for airfoils wall

1.3 数值验证

低雷诺数流动极其复杂，流动转捩的发生以及层流分离泡结构的产生对翼型阻力特性的影响极其显著[21]，因此较高的阻力计算精度往往是体现数值模拟精度的关键。考虑到目前非定常求解技术比较成熟，本文主要针对γ-Reθt转捩模型数值模拟低雷诺数复杂流动的能力进行验证。

参考美国伊利诺伊大学厄巴纳-香槟分校(UIUC)的低湍流度亚声速风洞试验条件与结果[22-23]，以FX 63-137翼型为算例对数值方法进行验证。计算状态为：雷诺数Re=2×105，3.5×105。图3给出了翼型升阻力系数(CL和CD)时均化计算结果与实验结果的对比。

由图3可知，宏观上2种雷诺数条件下计算结果与实验结果均吻合较好，在小迎角α下翼型升阻力计算相对误差不超过4%，而在大迎角状态下相对误差稍有增大。

图4给出了升阻力系数随时间变化收敛曲线。结果显示，在小迎角情况下数值收敛性较好，而在大迎角时升阻力系数随时间则呈现明显的周期性变化。由于太阳能飞机使用迎角一般较小，因此后文也主要关注小迎角范围内的气动特性变化趋势(如无特殊说明，下文给出的结果均为时均化结果)。

图3 时均化升阻力系数与实验结果对比
Fig.3 Comparison of lift and drag coefficients between time-averaged results and experimental results

图4 升阻力系数随时间的变化
Fig.4 Variation of lift and drag coefficients with respect to time

2 计算结果分析

2.1 不同雷诺数下拟合优度对翼型宏观气动特性的影响

针对不同雷诺数条件下各拟合优度折线型模型气动特性进行数值模拟分析。计算状态为：Re=1×105，3×105，1×106。图5为各折线型翼型与基准翼型的时均化计算升力系数CL、阻力系数CD及升阻比K曲线对比。

由图5可知，3种雷诺数条件下升阻特性曲线随拟合优度变化呈现出2种不同的变化趋势：① 雷诺数为1×105时，5种折线型翼型在-6°～6° 迎角范围内升阻性能优于Baseline翼型，典型迎角4°下，随拟合优度减小，升力先增大后减小，阻力逐渐减小；② 雷诺数为3×105和1×106条件下，折线型翼型气动特性能与Baseline翼型基本持平，并随着拟合优度的减小，气动性能逐步恶化。

此外，值得注意的是，雷诺数从3×105增加到1×106：与Baseline翼型升阻特性基本持平的折线型翼型最小拟合优度从0.999 0增大为0.999 5；对于确定拟合优度的翼型，如折线型“100”翼型(拟合优度为0.999 5)，能与Baseline翼型升阻特性基本持平的最大迎角从8° 提前为4°。

图5 不同雷诺数下各拟合优度翼型的时均化升阻特性
Fig.5 Time-averaged lift and drag characteristics of airfoils with different goodness of fit at different Reynolds numbers

2.2 低雷诺数条件折线型翼型增升减阻机理分析

2.2.1 增升机理

根据实际调查研究我们呢可以看出，随着信息化管理和互联网时代的发展，建筑产业已经逐渐建立起了以社会实际需求和行业发展需要为目标的O2O平台、有效搭建起了以承发包交易需求为核心的交易平台、以B2B供应链为任务的一站式服务平台。但是在实际交易和工作过程中，很多企业和集团施工现场的管理上都停留在十分表面，宏观的控制性指标数据只是表面的交互。建筑产业施工现场管理过程中，很多材料、工程进度、工程质量等细微的数据及相关的参数和材料等级等等并没有通过专业的平台进行共享，而是通过微信、QQ、邮箱等非专业化的平台进行传输。

图6为Re=1×105时各折线型翼型与基准翼型在典型迎角α=4° 下的时均压力分布对比，图中x/c为翼型表面位置与翼型弦长之比。

图6 Re=1×10、α=4° 时翼型表面时均压力分布对比
Fig.6 Comparison of time-averaged pressure distributions on airfoil surface when Re=1×10， α=4°

由图6可以看出，相比于Baseline翼型光滑连续的压力分布曲线，折线型翼型上表面压力系数Cp出现了多次峰值与谷值的波动变化；在各段折线范围，压力先增大后减小，这表明在各折线段上，翼型表面附面层内流动先膨胀后压缩；尽管折线型翼型上下表面压力分布形态相比于Baseline翼型存在波动变化，但其压力分布曲线所围成的面积相对变化并不大，仅稍有增加，其翼型计算升力系数也稍有增大，而该升力增量主要来源于翼型上表面二次吸力峰及其下游压力平台，这正与第2段折线范围相对应，并且二次吸力峰明显与第1段折线长度有关。因此，第2段折线的长度及位置对升力增加起主要作用。

2.2.2 减阻机理

表2给出了4° 迎角时各翼型上表面转捩位置及其阻力系数计算值。可以看出，随着拟合优度的减小，流动转捩位置提前，压差阻力也不断减小，摩擦阻力先减小后增大，总阻力逐渐减小。

分析折线型翼型压差阻力减小的原因。由图6 可以看出，对比Baseline翼型，折线型翼型计算压力分布前缘吸力峰值增大，压力平台后存在一定范围的低压差区，考虑到基准翼型弯度较大，从升阻力积分计算方法的角度出发，其压差阻力相应有所减小，并且拟合优度越小的折线型翼型(第1段折线及压力恢复区折线长度越大)，其压差阻力越小。

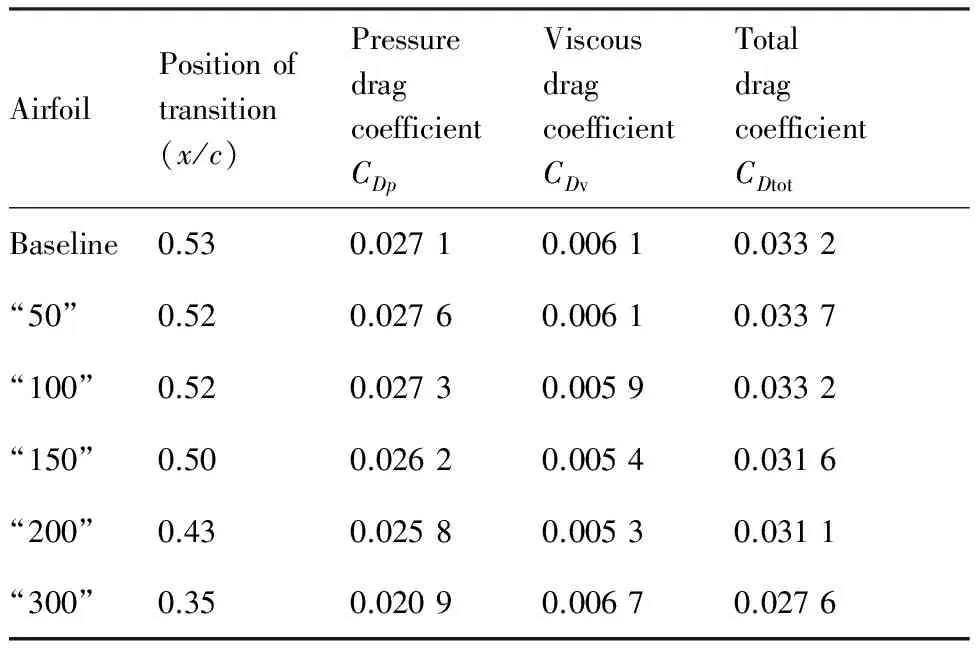
表2 不同拟合优度翼型转捩位置与阻力系数(α=4°)

分析摩擦阻力变化的原因。对比Baseline翼型，折线型“150”翼型尽管转捩位置由0.53倍弦长提前到0.50倍弦长处，其摩擦阻力却有所减小，而折线型“300”转捩位置提前为0.35倍弦长处，摩擦阻力有所增大。图7为4°迎角下Baseline翼型、折线型“150”和“300”翼型表面时均摩擦阻力Cf对比。由图7可知，折线转折突变使得翼型表面摩擦阻力也出现了对应于压力变化的峰谷波动变化。两折线型翼型摩擦阻力分布的主要区别在于翼型上表面压力恢复区，说明折线型翼型摩擦阻力的减小或增大可能与其压力恢复区折线长度有关。

图7 4° 迎角下时均表面摩擦阻力分布对比
Fig.7 Comparison of time-averaged skin friction drag distribution when α=4°

图8为4°迎角下Baseline翼型、折线型“150”、“200”和“300”翼型时均表面流场结构对比,图中KT为湍流动能。

图8 4° 迎角下翼型时均表面流场结构
Fig.8 Time-averaged flow structures of airfoil surface when α=4°

由图8可知，Baseline翼型上表面0.4～0.8弦长范围出现了典型的低雷诺数长层流分离泡结构，分离泡较长且厚度较大，能量损失相对最为严重。相比Baseline翼型，折线型翼型分离转捩提前，上表面出现覆盖范围较大的多个分离涡结构，攀附在各折线段范围内，分离回流区较大，虽然出现了近前缘处附面层分离，但分离后很快再附，这些分离涡厚度较小，能量损耗小。可以发现，折线型“150”和“200”翼型湍动能云图分布出现了波动变化，对比Baseline翼型流动结构发生了较大变化。为了探究其原因，取Baseline和折线型“150”翼型升力系数收敛曲线，如图9所示，Baseline翼型计算结果收敛较好，而在相同的状态下，折线型“150”翼型计算升力系数随时间则呈周期性变化。

图10为折线型“150”翼型单个周期T内不同时刻的非定常流线。由图10可知，折线型“150”翼型上表面存在多个小分离涡，并随时间向下游运动，直至脱落消失，同时在分离点之后又不断产生新的涡。分离涡的生成、脱落均呈明显的周期性。而随着折线型翼型拟合优度进一步减小(压力恢复区折线长度增加)，这种现象逐渐减弱直至消失。综合来看，流动结构较大的改变是折线型翼型摩擦阻力发生不同变化的原因，这主要受压力恢复区折线长度的影响。

图9 升力系数随时间的变化
Fig.9 Variation of lift coefficients with respect to time

图10 单个周期内不同时刻非定常流线
Fig.10 Unsteady streamline corresponding to one time period

2.3 耦合太阳能电池布局设计的折线型翼型优化设计思想初步验证

通过以上研究可以发现，靠近翼型前缘的前两段折线长度以及压力恢复区的折线长度将对前缘吸力峰值、二次吸力峰的位置、层流分离泡出现的范围等流动特征产生影响，这是决定折线型翼型气动性能的主要因素。

因此，在耦合太阳能电池布局设计，对低雷诺数折线型翼型设计的过程中，以不破坏整体流动结构，不降低整体升力为前提，提出以下3条设计准则：

1) 适当增大第1段折线长度，增大前缘吸力峰值，提高前缘附近升力贡献,减小压差阻力。

2) 第2段折线适当加长，扩大压力平台范围，增加升力。

3) 选择合适的压力恢复区折线长度，不能太大或者太小，尽可能诱导形成多个小而薄的分离涡结构，减小摩擦阻力。

为了验证上述设计思想准则，在折线型“300”翼型基础上增大第1段折线长度建立MOD1、在压力恢复区选择150 mm长度折线建立MOD2以验证设计思想准则1)和3)；在MOD2基础上增大第2段折线长度以验证设计思想准则2)。表3所示为3种折线型模型MOD1、MOD2、MOD3的具体说明。计算状态与前文一致：Re=1×105，α=4°。计算结果如表4所示，给出了设计折线型翼型计算升阻力系数。

表3 3种折线型翼型说明Table 3 Description of three types of broken line airfoils

表4 3种折线型翼型及Baseline翼型的升阻力系数

下面针对本文所提出的3条设计思想准则一一进行验证分析：

1) 由表4结合表2可知，随折线型翼型第1段折线长度增大，压差阻力减小，直到第1段折线长度增大至300 mm(MOD1)，对比折线型“300”翼型(第1段折线为200 mm)，MOD1压差阻力再次增大。图11所示为MOD1翼型表面流场结构，可以看到MOD1在第1段折线范围就存在层流分离结构，这主要是因为其第1段折线突变太剧烈，导致原流动结构受到破坏。因此，第1段折线长度应尽可能长，但需小于300 mm。

2) 由表2和表4可知，MOD2摩擦阻力相比折线型“300”翼型下降约21%，相比折线型“100”翼型下降约10%，说明MOD2压力恢复区折线长度选择较为合适。

3) 对比MOD3与MOD2，MOD3在MOD2基础上增大了第2段折线长度，结果发现升力有所增加，压差阻力减小约7.8%。

如上所述，本文所提出的3条低雷诺数折线型翼型设计思想准则一一得到验证。图12为时均化压力分布对比，图13为MOD3时均化流场结构。由图可知，MOD3的前缘吸力峰最大，压力平台范围最长，压力恢复区存在较大范围低压差区，翼型上表面存在多个分离涡结构。对比Baseline翼型，改善后的MOD3升力增加约6.3%，阻力减小约16.6%，升阻比增加约27.2%，优化效果显著。

图11 4° 迎角下MOD1表面流场结构
Fig.11 Flow structures of MOD1 surface when α=4°

图12 翼型表面时均化压力分布对比
Fig.12 Comparison of time-averaged pressure distributions on airfoil surface

图13 MOD3时均化流场结构
Fig.13 Time-averaged flow structure of MOD3

3 结 论

1) 雷诺数为1×105时，-6°～6° 迎角范围内，不同拟合优度折线型翼型升阻特性相比基准翼型有不同程度的优势；随着雷诺数增加，折线型翼型升阻方面的优势逐渐消失，并且雷诺数越大，能与基准翼型升阻特性基本持平的折线型翼型拟合优度越大。

2) 低雷诺数小迎角条件下，与Baseline翼型对比，折线型翼型折线段突变造成压力分布出现二次吸力峰，同时增加了对附面层的扰动，层流附面层“分离—转捩—再附”，形成分离泡，在二次吸力峰下游形成压力平台，这是折线型翼型升力增大的主要原因；翼型前缘峰值增大以及上表面分离结构的改变，使压差阻力和摩擦阻力分别得到减小，这是折线型翼型阻力较小的主要原因。

3) 依据本文提出的设计思想准则，设计算例，通过气动力参数的对比分析，初步验证了该设计思想的可行性与实用性，具有一定参考价值。

低雷诺数条件下，基于工程应用的折线型翼型相比光滑基准翼型表现出了一定潜力，对于太阳能飞机的工程研制有较大的参考意义。但是，不同太阳能飞机飞行任务雷诺数不同，选取的基准翼型不同，需考虑电池组件效率，对最优拟合优度折线型翼型进行更加详细的优化设计。

[1] 马东立, 包文卓, 乔宇航. 利于冬季飞行的太阳能飞机构型研究[J]. 航空学报, 2014, 35(6): 1581-1591.

MA D L, BAO W Z, QIAO Y H. Study of solar-powered aircraft configuration beneficial to winter flight[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(6): 1581-1591 (in Chinese).

[2] 昌敏, 周洲, 王睿. 基于机翼-帆尾的高纬度跨年驻留太阳能飞机总体参数设计方法[J]. 航空学报, 2014, 35(6): 1592-1603.

CHANG M, ZHOU Z, WANG R. Primary parameters determination for year-round solar-powered aircraft of wing-sail type at higher latitudes[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(6): 1592-1603 (in Chinese).

[3] Boucher R. History of solar flight[C]//20th Joint Propulsion Conference. Reston: AIAA, 1984: 1429.

[4] NOLL T E, BROWN J M, PEREZ-DAVIS M E, et al. Investigation of the Helios prototype aircraft mishap: Volume I Mishap report[R]. Hampton, VA: Langley Research Center, 2004.

[5] PINES D J, BOHORQUEZ F. Challenges facing future micro-air-vehicle development[J]. Journal of Aircraft, 2006, 43(2): 290-305.

[6] 甘文彪, 周洲, 许晓平. 仿生全翼式太阳能无人机气动数值模拟[J]. 航空学报, 2015, 36(10): 3284-3294.

GAN W B, ZHOU Z, XU X P. Aerodynamic numerical simulation of bionic full-wing typical solar-powered unmanned aerial vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3284-3294 (in Chinese).

[7] MUELLER T J, DELAURIER J D. Aerodynamics of small vehicles[J]. Annual Review of Fluid Mechanics, 2003, 35(1): 89-111.

[8] 李锋, 白鹏, 石文, 等. 微型飞行器低雷诺数空气动力学[J]. 力学进展, 2007, 37(2): 257-268.

LI F, BAI P, SHI W, et al. Low Reynolds number aerodynamics of micro air vehicles[J]. Advances in Mechanics, 2007, 37(2): 257-268 (in Chinese).

[9] ROSS H. Fly around the world with a solar powered airplane[J]. Power, 2008, 1(8): 1-11.

[10] NOTH A. Design of solar powered airplanes for continuous flight[D]. Zurich: Swiss Federal Institute of Technology Zurich, 2008: 91-95.

[11] WALSH M J. Turbulent boundary layer drag reduction using riblets[C]//20th Aerospace Sciences Meeting. Reston: AIAA, 1982.

[12] WALSH M J. Riblets as a viscous drag reduction technique[J]. AIAA Journal, 1983, 21(4): 485-486.

[13] CHOI J, JEON W P, CHOI H. Mechanism of drag reduction by dimples on a sphere[J]. Physics of Fluids, 2006, 18(4): 1-4

[14] BEIERLE T, ANDERSON JR J D, RANZENBACH R C. Computational investigation of roughness related lift enhancement to symmetric airfoils[C]//17th Applied Aerodynamics Conference, Fluid Dynamics and Co-located Conferences. Reston: AIAA, 1999.

[15] 方洪, 张正科, 高超. 翼面几何不规则性对压力分布影响的数值模拟研究[J]. 科学技术与工程, 2011, 11(29): 7160-7167.

FANG H, ZHANG Z K, GAO C. Numerical simulation study of the effects of airfoil surface geometric irregularity on pressure distribution[J]. Science Technology and Engineering, 2011, 11(29): 7160-7167 (in Chinese).

[16] 张骏, 袁奇, 吴聪, 等. 大型风力机叶片表面粗糙度效应数值研究[J]. 中国电机工程学报, 2014, 34(20): 3384-3391.

ZHANG J, YUAN Q, WU C, et al. Numerical simulation on the effect of surface roughness for large wind turbine blades[J]. Proceeding of the CSEE, 2014, 34(20): 3384-3391 (in Chinese).

[17] 呼文韬. 太阳能飞行器太阳能能源系统的设计与实现[D]. 天津: 天津大学, 2013: 15-26.

HU W T. Design and implementation of power system for solar energy air vehicle[D]. Tianjin: Tianjin University, 2013: 15-26 (in Chinese).

[18] MENTER F R, LANGTRY R B, LIKKI S R, et al. A correlation-based transition model using local variables—Part I: Model formulation[J]. Journal of Turbomachinery, 2006, 128(3): 413-422.

[19] LANGTRY R B, MENTER F R, LIKKI S R, et al. A correlation-based transition model using local variables—Part II: Test cases and industrial applications[J]. Journal of Turbomachinery, 2006, 128(3): 423-434.

[20] WEIDER A, LEVY H, REGEV I, et al. SunSailor: Solar powered UAV[R]. Haifa, Israel: Aerospace Engineering Faculty, Technion—Israel Istitute of Technology, 2007.

[21] 陈立立, 郭正. 基于γ-Reθt转捩模型的低雷诺数翼型数值分析[J]. 航空学报, 2016, 37(4): 1114-1126.

CHEN L L, GUO Z. Numerical analysis for low Reynolds number airfoil based onγ-Reθttransition model[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(4): 1114-1126 (in Chinese).

[22] SELIG M S, GUGLIELMO J J, BROEREN A P, et al. Summary of low speed airfoil data—Vol. 1[M]. Virginia Beach, VA: SoarTech Publication, 1995: 87-93.

[23] MCGRANAHAN B D. Wind tunnel aerodynamic tests of six airfoils for use on small wind turbines[J]. Urbana, 2004, 51: 61801.

ResearchonlowReynoldsnumberairfoilsbasedonapplicationofsolar-poweredaircraft

LIUXiaochun1,2,ZHUXiaoping2,ZHOUZhou1,2,*,WANGKelei1,2

1.SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.ScienceandTechnologyonUAVLaboratory,NorthwesternPolytechnicalUniversity,Xi’an710065,China

Basedonsolar-poweredaircraft,numericalsimulationiscarriedoutforbrokenlineairfoilsmodeledwithtypicallowReynoldsnumbersFX63-137airfoiltosimulatetheinfluenceoftypicalcrystallinesiliconsolarcellsonaerodynamicshape.Thedefinitionof“goodnessoffit”isusedtodescribethedegreeofmatchingbetweenbrokenlineairfoilprofileandthereferenceairfoil(Baseline).Fivebrokenlineairfoilswithdifferentgoodnessoffitareestablished.Withcomputationalfluiddynamics(CFD)method,theaerodynamiccharacteristicsofdifferentbrokenlineairfoilsatdifferentReynoldsnumbersareanalyzed,andtheflowmechanismofthebrokenlineairfoilisstudiedinparticular.Basedontheactualneedsofengineeringapplications,themethodoflayingsheetsofcrystallinesiliconsolarcells,whichisalsothedesigncriteriaofbrokenlineairfoil,isproposed,andexamplesareusedtoverifytheeffectivenessofthemethod.TheresultsshowthattheaerodynamicperformanceofbrokenlineairfoilsisbetterthanthatofthebaselineairfoilatlowReynoldsnumbertosomeextent.However,withtheincreaseoftheReynoldsnumber,advantagesofbrokenlineairfoilsinliftanddragperformancedisappear.Pressuredistributionofthebrokenlineairfoilisinfluencedbythelengthofbrokenlinesandleadingedgesuctionpeak,regionofpressureplateauanddistributioninpressurerecoveryzonearethemainfactorsdeterminingtheaerodynamicperformanceofbrokenlineairfoils.Theproposeddesigncriteriaforbrokenlineairfoilsareverifiedthroughdesignedexamples.

solar-poweredaircraft;engineeringapplication;brokenlineairfoil;goodnessoffit;lowReynoldsnumber;aerodynamicperformance

2016-05-20；Revised2016-06-27；Accepted2016-07-17；Publishedonline2016-08-011037

URL：www.cnki.net/kcms/detail/11.1929.V.20160801.1037.004.html

s：CivilAircraftSpecificProject(MIZ-2015-F-009);ShaanxiProvinceScienceandTechnologyCo-ordinationProject(2015KTCQ01-78)

2016-05-20；退修日期2016-06-27；录用日期2016-07-17； < class="emphasis_bold">网络出版时间

时间：2016-08-011037

www.cnki.net/kcms/detail/11.1929.V.20160801.1037.004.html

民机专项 (MIZ-2015-F-009)； 陕西省科技统筹项目 (2015KTCQ01-78)

＊

.E-mailzhouzhou@nwpu.edu.cn

刘晓春， 祝小平， 周洲， 等． 基于太阳能飞机应用的低雷诺数翼型研究J． 航空学报,2017,38(4):120459.LIUXC,ZHUXP,ZHOUZ,etal.ResearchonlowReynoldsnumberairfoilsbasedonapplicationofsolar-poweredaircraftJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):120459.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0213

V211

A

1000-6893(2017)04-120459-11

(责任编辑： 鲍亚平， 徐晓)

＊Correspondingauthor.E-mailzhouzhou@nwpu.edu.cn