多回路气动伺服弹性系统稳定裕度的变结构μ分析方法

刘祥， 孙秦

西北工业大学 航空学院， 西安 710072

多回路气动伺服弹性系统稳定裕度的变结构μ分析方法

刘祥， 孙秦*

西北工业大学 航空学院， 西安 710072

作为一个多输入多输出(MIMO)系统，气动伺服弹性系统的各控制回路是相互耦合的，但对于各控制回路的稳定裕度目前尚无统一的计算方法。针对MIMO控制系统的稳定裕度计算问题，首先分析了现有的回差阵奇异值方法和μ分析方法，并指出了2种方法各自保守性的来源。在此基础上，提出了一种变结构μ分析方法，通过迭代调整扰动模型结构来求解稳定裕度，并从理论上证明了算法的单调收敛特性。以某弹性飞机的阵风减缓控制系统为例进行了稳定裕度分析。3种方法结果的对比表明，本文方法能够有效降低分析结果的保守性。

气动伺服弹性； 多输入多输出系统； 耦合； 稳定裕度； 变结构μ分析

作为涉及柔性飞行器结构、非定常气动力和飞行控制系统三者相互作用的多学科技术，气动伺服弹性技术已成为现代飞行器设计的关键内容。由于关系到飞行安全，气动伺服弹性系统的稳定性分析问题一直备受研究者关注[1-2]。在实际工程中，要实现机动控制、载荷减缓、乘坐品质改善及颤振抑制等目的需要多个控制面的参与，这使控制系统具有多个输入输出通道，如何有效分析并衡量控制回路的扰动稳定性依然是具有挑战性的问题。

经典单输入单输出(SISO)线性系统的稳定裕度一般通过幅值裕度和相位裕度来度量，且有多种精确计算方法。然而对于各回路之间存在耦合的多输入多输出(MIMO)线性系统，若直接采用SISO线性系统的分析方法来求解稳定裕度，得到的结果往往不尽人意[3]。文献[4-5]通过在控制回路中引入对角扰动矩阵并计算回差阵最小奇异值的方法，得到了MIMO线性系统各控制回路的幅值和相位同时变化时的稳定裕度，并获得了广泛的工程应用[6-7]。Doyle[8]通过定义结构奇异值μ(ω)来分析具有结构不确定性的MIMO线性系统的鲁棒稳定性。此后，Lind和Brenner[9]提出了基于μ分析的多回路系统稳定性评估方法，可用来确定不同类型的模型不确定性同时存在时气动伺服弹性系统的稳定飞行范围。Tsao等[10]在μ方法的基础上通过构造双线性变换模型给出了判断多回路系统是否满足给定幅值和相位裕度的充分条件。Vartio等[11]采用μ方法检验了多回路系统的幅值裕度和相位裕度。针对具有多个实参数扰动的系统，文献[12-13]根据映射理论提出了一种稳定裕度的精确计算方法，但这种算法的复杂度太高且迭代计算量过大。Al-Shamali等[14]基于频域下的Nyquist理论定义了临界扰动半径与临界方向等概念，并以此为基础计算SISO线性系统的Nyquist鲁棒稳定裕度，Son等[15]将这一理论推广到了MIMO线性系统。李信栋和苟兴宇[16]利用系统回差阵提出了2种稳定裕度改进方法，并将两者的结果与回差阵奇异值法的结果综合得到了保守性相对较低的结果。

针对多回路气动伺服弹性系统的稳定裕度问题，本文首先分析了现有的回差矩阵奇异值方法和μ分析方法，发现回差阵奇异值方法的保守性来自于方法本身，而μ分析方法的保守性主要是因建模时扰动模型的构造方式所致。为此，本文提出了一种变结构μ分析方法，通过迭代调整扰动模型的结构求解多回路控制系统的稳定裕度，可较好地提高稳定裕度估计精度，并对迭代参数施加约束以保证算法的快速收敛特性。最后，以一弹性飞机为例，采用不同方法计算比较了其阵风减缓控制系统的稳定裕度，验证了本文方法的优势。

1 回差阵奇异值法

本节对回差阵奇异值法进行理论推导。系统模型如图1所示，其中P(s)和K(s)分别为被控对象和控制系统，定义系统回差阵为I+K(s)P(s)。在输入端引入扰动量测阵

E(s)=diag{klexp(iφl)}l=1,2,…,n

(1)

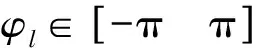
若闭环系统是渐进稳定的，则回差阵必满足det(I+KPE)≠0，根据奇异值的性质，则有

(2)

稳定裕度即研究系统在稳定范围内，量测阵

图1 系统模型
Fig.1 System model

E(s)中kl和φl同时变化的最大容许值。由E(s)的定义可知kl不为零，故E(s)非奇异。而由原闭环系统稳定可知I+KP非奇异，利用矩阵分离特性可得

I+KPE=

(3)

进一步，若闭环系统稳定则

(4)

(5)

结合式(4)和式(5)可得系统稳定的充分条件为

(6)

应用式(1)，式(6)等价于

(7)

记回差阵最小奇异值为m,根据式(7)，分别令所有φl=0°或所有kl=1，可得到多回路线性系统的幅值裕度GM和相位裕度PM表达式为

(8)

通过上面的分析可看出，保证系统稳定的条件式(6)是一个保守条件。对于某些具体问题，这种近似可能带来过大的保守性，以致影响到对控制系统的选择和评估。

2 μ分析方法

本节介绍多回路系统稳定裕度的μ分析方法。μ方法的基本处理途径是将模型分解为名义模型部分(即确定性部分)和幅值有限的不确定性部分。为此，将式(1)中的扰动量测阵表示为

E(s)=I+Δ=diag{klexp(iφl)}

l=1,2,…,n

(9)

式中：Δ为对角复数不确定性矩阵，即

Δ=diag{δ1,δ2,…,δn}δl∈C;l=1,2,…,n

结合式(9)，图1可转换为图2中的鲁棒稳定性分析结构，其中系统传递函数矩阵为

图2 鲁棒稳定性分析结构
Fig.2 Robust stability analysis structure

(10)

对于M∈Cn×n，定义其结构奇异值为

μΔ(M)=

(11)

若无Δ1∈Δ使det(I-MΔ1)=0，则μΔ(M)=0。

从式(11)中的定义可以看出，μΔ(M)的倒数是导致反馈系统失稳的摄动量最小值。因此可得到闭环系统鲁棒稳定的充要条件为

(12)

结合式(9)，式(12)等价于

l=1,2,…,n

(13)

分别令所有φl=0° 或所有kl=1，可得到幅值裕度GM和相位裕度PM表达式为

(14)

通过以上分析可以看出，式(12)是图2中模型鲁棒稳定的充要条件。但因式(9)中Δ各对角元素的幅值|δl|与E(s)各对角元素的幅值|kl|之间并非单调关系，从M的鲁棒稳定性出发估计图1中系统的稳定裕度势必会为结果引入保守性。另外，式(14)中幅值裕度与相位裕度间的一一对应关系并不符合客观情况，这也从另一方面证实了此方法的保守性。

3 变结构μ分析方法

为克服式(9)中由扰动量测阵的构造方法产生的保守性。在其基础上引入参数γ并重新定义E(s)为

E(s)=γI+Δ=diag{klexp(iφl)}

l=1,2,…,n

(15)

此时图1的等价模型如图3所示。

图3 有摄动的多回路系统
Fig.3 Multiloop system with perturbation

以式(15)为基础构造图2中所示的鲁棒稳定性分析模型，可得

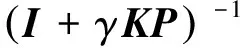
(16)

对应不同的γ取值，可求得不同的幅值裕度和相位裕度。下面对γ的取值方法进行讨论。

当固定γ的取值时，由式(12)和式(15)可知闭环系统稳定的充分必要条件为

l=1,2,…,n

(17)

式中:μΔ,γ(M)为给定γ时的结构奇异值。令式(17)中所有φl=0° 可得

l=1,2,…,n

(18)

(19)

令式(17)中所有kl=1可得

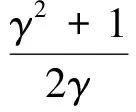
(20)

易推得式(20)有解的充分必要条件为

(21)

这等价于

(22a)

(22b)

即γ在取值时必须满足式(22a)和式(22b)的约束。

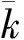
(23)

将式(22a)和式(23)两侧分别相加可得

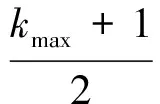
(24)

参考式(24)，以γ为参变量迭代求解图3中多回路系统的稳定裕度。令初始值为1，取迭代公式为

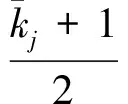
(25)

定理1根据式(25)迭代求解稳定裕度时，增益裕度单调递增且收敛。

证明证明过程分以下2步：首先证明增益上界随γ的增大而增大，再证明迭代过程中增益裕度的单调收敛性。

1) 对于第j次和第j+1次迭代，由式(17)可知其幅值和相位边界分别满足

(26a)

(26b)

这2条边界必有交点。当γj+1>γj时，易知在交点处式(26)各变量满足图4中的三角形关系。

此时，2次迭代过程中的增益上界满足

|AD|+|CD|-|AB|-|CB|=

|BD|+|CD|-|CB|>0

(27)

即增益上界随γ的增大而增大。

2) 当γ=γ1时显然满足式(22a)和式(22b)。现假设γ=γj时同样满足式(22a)和式(22b)，则当γ=γj+1时满足

图4 变量关系图
Fig.4 Variable relation graph

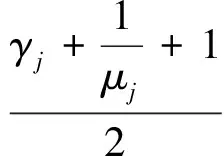
j=1,2,…

(28)

由数学归纳法知γ是单调递增的，故迭代过程中增益上界也是单调递增的。参考图4可得，增益下界满足

|AD|-|CD|-|AB|+|CB|=

|BD|+|CB|-|CD|>0

(29)

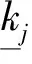
(30)

即增益下界收敛于1。式(30)即可作为迭代过程的收敛判据。

综上可知，增益裕度单调递增且收敛。定理1得证。

实际上每次迭代过程得到的稳定区域边界与系统的真实稳定区域边界至少有1个交点，而各次迭代得到的稳定区域的并集可以一定程度上逼近实际的稳定区域，因此在迭代过程中减小γ的增量可以得到保守性更低的稳定区域。但为了加速幅值裕度的收敛过程仍依据式(25)更新γ参数。虽然在迭代过程中相位裕度并无单调收敛特性，但可以通过将其取为各次迭代中的最大值以最大程度地降低保守性。

根据以上讨论可将迭代过程描述如下：

1) 令迭代序号j=1，γj=1，PM=0°。

2) 根据式(16)求解M，并根据μ分析理论计算结构奇异值μj。

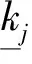
(31)

若PM<φj，则令φj→PM，其中“→”表示赋值运算。

4) 判断迭代是否收敛。若是，转至步骤5)；否则根据式(25)更新γ，并令j+1→j，再转至步骤2)。

5) 按式(32)计算GM，结束循环。

(32)

需要注意的是，本文针对的是多输入多输出系统控制回路的稳定裕度计算问题，因此并未具体考虑模型的参数不确定性和未建模不确定性，这似乎限制了本文方法的用途。但实际上并非如此，这可以从以下2个方面解释：

首先，本文的稳定裕度计算问题是一个相对独立的问题，对于系统参数变化或建模误差较小情况下的系统稳定裕度可得到相对其他方法保守性更低的结果。

其次，对于模型的参数不确定性或未建模不确定性不可忽略的情况，可将其此类不确定性加入文中的算法结构，并与式(9)中代表回路增益和幅值变化的复数不确定块Δ合并为阶数更高的不确定块。然后通过调整算法结构可以进一步分析此类模型的控制回路稳定裕度。但这样处理的价值和意义有待商榷，因为对于模型不确定性不可忽略的情况，系统的鲁棒稳定性分析结果往往是以不确定参数或未建模不确定性的鲁棒稳定范围的形式给出[9]，且已有成熟的分析方法。当然，也可以将本文方法直接应用于名义模型，得到的稳定裕度结果可以作为前述结果的补充，从控制回路的角度反映闭环系统的鲁棒稳定性。

4 算 例

4.1 算例模型1

为验证本文方法的有效性，首先对文献[16]中的双输入双输出控制系统进行稳定裕度分析。被控对象和控制器的传递函数矩阵分别为

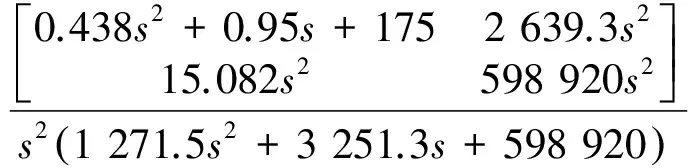
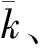
表2给出了分别由本文方法、回差阵奇异值法和μ分析方法计算出的控制回路稳定裕度。易知本文的变结构μ分析方法具有最低的保守性。

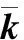
表1 增益上界、增益下界和相位裕度的收敛过程Table 1 Convergence process of ， and PM

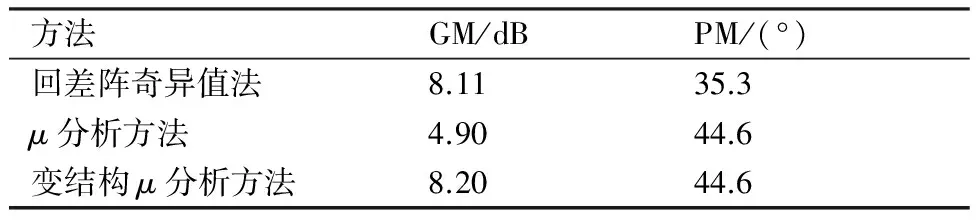
表2 不同方法对算例1的稳定裕度计算结果

4.2 算例模型2

以文献[17]中的弹性飞机模型为基础，对设计出的H∞阵风减缓控制系统进行稳定裕度分析。飞机的气动力模型如图5所示，飞行马赫数和高度分别为0.3和5 000 m。具体模型数据见文献[18]。

图5 飞机气动力模型
Fig.5 Airplane aerodynamic model

在构造全机状态空间模型时，结构模态取为全机对称的前7阶弹性模态及刚体俯仰和沉浮模态。在构造时域非定常气动力模型时，采用最小状态法[17]对由ZAERO软件计算得到的频域广义气动力进行拉氏域有理拟合，选取4个气动力滞后根并对其进行非线性优化以减小拟合误差。滞后根最终取值为[-0.110 -0.297 -0.307 -0.530]。传感器输出为重心处俯仰速率及翼尖过载，控制面采用升降舵和副翼，对应的舵机传递函数均为

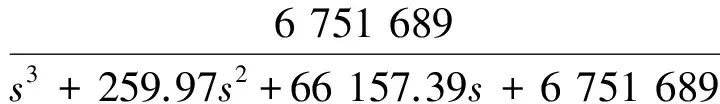
采用离散“1-cos”型阵风模型，垂直阵风速度在飞行轨迹方向的分布如图6所示。

根据MATLAB的鲁棒控制工具箱设计H∞控制器，设计目标为减缓阵风引起的翼根弯矩和俯仰速率响应。因控制器的设计过程与本文主题无关，故在此不予赘述，而仅在附录A中给出其降阶后的状态空间模型。易知控制系统为双输入双输出的多回路耦合系统，系统框图如图7所示。图8给出了翼根弯矩和俯仰速率的开环和闭环离散阵风响应。从图中可看出闭环系统稳定，且翼根弯矩和俯仰速率得到了有效抑制。

采用本文方法分析上述控制回路稳定裕度时，迭代过程在第4次循环达到收敛。表3给出了由本文方法、回差阵奇异值法和μ分析方法计算出的控制回路稳定裕度结果，可以看出本文方法的保守性最低。为保持闭环系统稳定，两条控制回路的相位不变时可容许的最大增益为8.68 dB；两条回路的增益不变时可容许的最大相位滞后为63.0°。

图6 离散阵风
Fig.6 Discrete gust

图7 弹性飞机阵风减缓控制方案
Fig.7 Gust alleviation control scheme of elastic aircraft

下面进一步通过时域仿真对上述结果进行验证。根据计算结果可知各回路相位不变时幅值可同时增大2.71倍。图9(a)分别给出了幅值同时增大2.71倍时翼尖过载及飞机俯仰速率的阵风响应，图9(b)分别给出了幅值同时增大2.74倍时翼尖过载及飞机俯仰速率的阵风响应。

从图9可以看出，控制回路增益同时增大2.71 倍时系统是稳定的，而增益继续增大到2.74倍时系统临界不稳定。由上述结果可知，利用本文提出的变结构μ分析方法得到的稳定裕度已足够逼近系统真实稳定裕度。

图8 翼根弯矩和俯仰速率的离散阵风响应
Fig.8 Wing root bending moment and pitch rate response to discrete gust

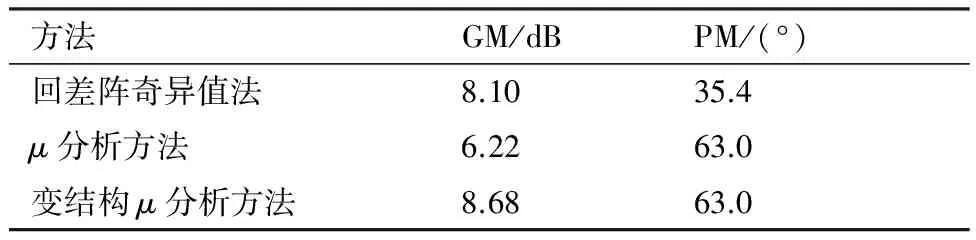
表3 不同方法对算例2的稳定裕度计算结果

图9 k=2.71和k=2.74时翼尖过载及俯仰速率的阵风响应
Fig.9 Wing tip overload and pitch rate response to gust with k=2.71 and k=2.74

5 结 论

1) 建立的变结构μ分析方法能够方便求解气动伺服弹性系统的稳定裕度，并具有比已有方法更小的保守性。

2) 建立的变结构μ分析方法在迭代过程具有单调收敛特性，能够快速求解系统的稳定裕度，且迭代次数并不随问题规模的增大而增大。

[1] HADDADPOUR H. Aeroservoelastic stability of supersonic slender-body flight vehicles[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(6): 1423-1427.

[2] KARPEL M, MOULIN B, CHEN P C. Extension of the g-method flutter solution to aeroservoelastic stability analysis[J]. Journal of Aircraft， 2005, 42(3): 789-792.

[3] DOYLE J C. Robustness of multiloop linear feedback systems[C]//Proceedings of the IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 1978: 12-18.

[4] LEHTOMAKI N A, SANDELL J N R, ATHANS M. Robustness results in linear-quadratic Gaussian based multivariable control designs[J]. Transactions on Automatic Control, 1981, AC-26(1): 75-93.

[5] MUKHOPADHYAY V, NEWSOM J R. Application of matrix singular value properties for evaluating gain and phase margins of multiloop systems[C]//AIAA Guidance and Control Conference. Reston: AIAA, 1982: 420-428.

[6] BURKEN J J. Flight-determined stability analysis of multiple-input-multiple-output control systems: AIAA-1992-4396[R]. Reston: AIAA, 1992.

[7] 吴斌, 程鹏. 多变量飞控系统的稳定裕度分析[J]. 航空学报, 1998, 19(6): 18-22.

WU B, CHENG P. Stability margin analysis of the multiloop flight control systems[J]. Acta Aeronautica et Astro-nautica Sinica, 1998, 19(6): 18-22 (in Chinese).

[8] DOYLE J. Analysis of feedback systems with structured uncertainties[J]. IEEE Proceedings D: Control Theory and Applications, 1982, 129(6): 242-250.

[9] LIND R, BRENNER M. Analyzing aeroservoelastic stability margins using theμmethod[C]//AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Reston: AIAA, 1998: 1672-1681.

[10] TSAO T T, LEE F C, AUGENSTEIN D. Relationship between robustnessμ-analysis and classical stability margins[C]//Proceedings of the 1998 IEEE Aerospace Conference. Part 1 (of 5). Piscataway, NJ: IEEE Press, 1998: 481-486.

[11] VARTIO E J, SHAW E E, VETTER T. Gust load alleviation flight control system design for a sensor craft vehicle[C]//26th AIAA Applied Aerodynamics Conference. Reston: AIAA, 2008: 1-10.

[12] DE GASTON R R E, SAFONOV M G. Exact calculation of the multiloop stability margin[J]. Transactions on Automatic Control, 1988, 33(2): 156-171.

[13] SIDERIS A, DE GASTON R R E. Multivariable stability margin calculation with uncertain correlated parameters[C]//Proceedings of the 25th IEEE Conference on Decision & Control. Piscataway, NJ: IEEE Press, 1986: 766-771.

[14] AL-SHAMALI S A, JI B, CRISALLE O D, et al. The Nyquist robust sensitivity margin for uncertain closed-loop systems[J]. International Journal of Robust and Nonlinear Control, 2005, 15(14): 619-634.

[15] SON J E, MANI A S, LATCHMAN H A. Robustness analysis for MIMO systems with unstructured uncertainties[C]//2010 8th IEEE International Conference on Control and Automation. Piscataway, NJ: IEEE Press, 2010: 1333-1337.

[16] 李信栋, 苟兴宇. 多输入多输出线性定常系统稳定裕度的分析与改进[J]. 控制理论与应用， 2014, 31(1): 105-111.

LI X D, GOU X Y. Analysis and improvement of stability margin for multi-input multi-output linear time-invariant systems[J]. Control Theory & Applications， 2014, 31(1): 105-111 (in Chinese).

[17] KARPEL M, MOULIN B, CHEN P C. Dynamic response of aeroservoelastic systems to gust excitation[J]. Journal of Aircraft， 2005, 42(5): 1264-1272.

[18] ZONA Technology, Inc. ZAERO application’s manual Vol.2[M]. Scottsdale: ZONA Technology, Inc. 2008: 121-198.

Variable-structureμsynthesismethodforstabilitymarginofmultiloopaeroservoelasticsystem

LIUXiang,SUNQin*

SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China

Aeroservoelasticsystemisamulti-input-multi-output(MIMO)systemwithitscontrolloopscoupledwitheachother,whilecurrentlythereisnounifiedtheoryinregardtothestabilitymarginofthecontrolloops.Thispaperaddressesthisproblembyfirstanalyzingtheexistingreturndifferencematrixmethodandtheμsynthesismethod,andthenproposinganewmethodtoreducetheconservativenessduringanalysis.Thisnewmethod,calledthevariable-structureμsynthesismethod,solvesthestabilitymarginthroughadjustingtheperturbationmodelinseveraliterationsandisprovedtohavefastconvergenceproperty.Finally,differentmethodsareusedtocalculatethestabilitymarginsofthegustalleviationsystemofaflexibleaircraft,andtheresultsshowthattheproposedapproachislessconservativecomparedwiththeexistingmethods.

aeroservoelasticity;multi-input-multi-outputsystem;coupling;stabilitymargin;variable-structureμsynthesis

2016-04-21；Revised2016-05-19；Accepted2016-06-21；Publishedonline2016-06-270836

URL：www.cnki.net/kcms/detail/11.1929.V.20160627.0836.004.html

.E-mailsunqin@nwpu.edu.cn

2016-04-21；退修日期2016-05-19；录用日期2016-06-21； < class="emphasis_bold">网络出版时间

时间：2016-06-270836

www.cnki.net/kcms/detail/11.1929.V.20160627.0836.004.html

＊

.E-mailsunqin@nwpu.edu.cn

刘祥， 孙秦． 多回路气动伺服弹性系统稳定裕度的变结构μ分析方法J． 航空学报,2017,38(4):120350.LIUX,SUNQ.Variable-structureμsynthesismethodforstabilitymarginofmultiloopaeroservoelasticsystemJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):120350.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0201

V249.1

A

1000-6893(2017)04-120350-09

(责任编辑： 鲍亚平， 张晗)

附录A:

控制器状态空间方程为

yc=Ccxc+Dcuc

式中：xc、uc和yc分别为控制器的状态变量、输入和输出；Ac、Bc、Cc和Dc分别为系数矩阵，取值如下：

Ac=

a11=-61.714 4,a12=328.244 5,a21=-328.244 5,a22=-61.714 4,a33=-224.140 3,a34=161.166 2,a43=-161.166 2，a44=-224.140 3,a55=-40.325 9,a56=244.077 8,a65=-244.077 8,a66=-40.325 9,a77=-18.982 0,a78=234.244 1,a87=-234.244 1,a88=-18.982 0,a99=-13.043 2,a9 10=211.119 6,a10 9=-211.119 6,a10 10=-13.043 2,a11 11=-53.624 0,a11 12=65.750 4,a12 11=-65.750 4,a12 12=-53.624 0,a13 13=-62.856 0,a14 14=-17.728 9,a14 15=63.133 9,a15 14=-63.133 9,a15 15=-17.728 9,a16 16=-24.524 5,a16 17=54.873 4,a17 16=-54.873 4,a17 17=-24.524 5,a18 18=-9.759 7,a19 19=-0.005 1,a20 20=-0.936 1