γ-Re θt-CF转捩模型在Spalart-Allmaras湍流模型中的推广及验证

鞠胜军， 阎超， 叶志飞

北京航空航天大学 航空科学与工程学院， 北京 100083

γ-Reθt-CF转捩模型在Spalart-Allmaras湍流模型中的推广及验证

鞠胜军， 阎超*， 叶志飞

北京航空航天大学 航空科学与工程学院， 北京 100083

横流(CF)不稳定性是三维流动中诱发转捩的一项非常重要的因素，考虑到γ-Reθt-CF转捩模型对流向Tollmien-Schlichting波和横流波不稳定性引起转捩的判定均是完全基于当地变量，且Spalart-Allmaras(SA)湍流模型计算效率高，因而将γ-Reθt-CF转捩模型与SA湍流模型相结合，并将其引入开源Standford University Unstructured(SU2)计算流体力学分析平台。为了考察和验证模型的预测精度，分别使用原始γ-Reθt模型和γ-Reθt-CF-SA模型，对NLF(2)-0415后掠翼型和标准6∶1椭球模型进行了转捩预测数值模拟。算例结果表明，γ-Reθt-CF-SA模型的计算结果与试验数据吻合程度远远优于原始γ-Reθt模型，γ-Reθt-CF-SA 模型能正确地预测出三维流动中的横流不稳定性引起转捩的现象。

转捩模型; 横流不稳定性; 基于当地变量; 动量厚度; 间歇因子

在航空工程领域，流动不稳定性主要是由接触线不稳定性、Taylor-Görtler涡不稳定性、流向Tollmien-Schlichting(T-S)波不稳定性和横流(CF)波不稳定性4种扰动波引发。其中，Taylor-Görtler涡不稳定可以通过消除壁面凹曲来避免。防止接触线转捩可以通过设计外形时使接触线雷诺数不要超过其临界值 。因而，T-S波引起的不稳定性和横流不稳定性是三维流动中最主要的机制[1]。

在三维流动边界层转捩预测方法中，直接数值模拟方法(DNS)[2]和大涡模拟方法(LES)[3]由于计算量过大很难应用到工程计算中；基于线性稳定性理论的方法[4-6]在求解过程中需要用到边界层动量厚度的信息，也难以在现代的CFD并行计算中实现，因而转捩模型方法成为工程领域转捩预测的主要方法。

在转捩模型的提出与构造方面，Coder和Maughmer[7]开发了基于放大因子的转捩模型、王亮和符松[8]开发了k-ω-γ转捩模型等。在航空工程领域运用最广泛的是由Langtry和Menter[9]在2005年提出的γ-Reθt与剪切应力输运(Shear-Stree Transport，SST)湍流模型相结合的γ-Reθt-SST转捩模型，该模型考虑了自然转捩、Bypass转捩和分离诱导转捩等多种转捩机制，集合转捩经验关系式和低雷诺数湍流模型的优势，并首先被耦合到SSTk-ω湍流模型中，由于模型提供了一个将经验公式进行当地化处理的框架，转捩的判别都基于当地变量(Local Correlation-Based)，因而大大提高了通用CFD用于求解复杂外形流动的能力，特别是对于三维复杂情况下的流动。Shivaji和James[10]实现了对γ-Reθt转捩模型与Spalart-Allmaras(SA)湍流模型的结合，构造了具有转捩预测能力的γ-Reθt-SA模型。但这些模型在构造中主要针对流向T-S波不稳定性引起的转捩，对于横流波不稳定性引起的转捩预测精度较差。由此，在转捩模型中考虑横流的影响得到了深入的研究，比如Jeong[11]、Comelia[12]、Medida[13]、Seyfert[14]、徐家宽[15]等在γ-Reθt转捩模型中，添加了横流转捩经验判据。但这些判据都不是完全基于当地变量信息，在求解时需要用到边界层动量厚度的信息，且没有考虑表面粗糙度对于横流转捩的影响。针对这些问题，Robin等[16]在2015年提出了完全基于当地变量的横流不稳定性边界层转捩预测方法，即γ-Reθt-CF模型，并将其与SSTk-ω湍流模型进行耦合构造出γ-Reθt-CF-SST模型，计算结果令人满意。γ-Reθt-CF模型没有推广耦合到其他湍流模型中，考虑到SA模型计算效率高，被广泛应用于航空工程的数值计算中，并很容易构造雷诺平均Navier-Stokes/LES(RANS/LES)混合方法。本文将γ-Reθt-CF模型与SA模型进行耦合构造出γ-Reθt-CF-SA模型，并引入开源Stanford University Unstructured(SU2)计算流体力学分析平台中。针对三维流动中典型的横流不稳定性引起边界层转捩问题，选取NLF(2)-0415后掠翼型和标准6∶1椭球模型作为验证算例，将预测的转捩起始位置和试验值进行对比分析，校验γ-Reθt-CF-SA模型的预测精度。

1 数值方法

1.1 γ-Reθt转捩模型

γ-Reθt转捩模型运用基于涡雷诺数来判断转捩起始位置，代替动量厚度雷诺数，实现了完全基于当地变量进行转捩判据，因而满足现在CFD技术大规模并行化的计算要求。模型由转捩动量厚度雷诺数和间歇因子2个输运方程组成。

1.1.1 转捩动量厚度雷诺数输运方程

控制转捩的起始位置是由转捩动量厚度雷诺数所决定，其值是由转捩动量厚度雷诺数方程求解得到。转捩起始雷诺数是一个由来流湍流度和来流压力梯度组成的非当地化的函数。转捩动量厚度雷诺数输运方程的生成项由不同的经验公式组成，方程为

(1)

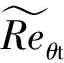
在式(1)中生成项为

(2)

式中：Reθt为转捩动量厚度雷诺数；Fθt为开关函数，(1-Fθt)项用于识别边界层，在边界层由内到外，由0变化到1。源项系数Cθt=0.03，扩散项系数σθt=2.0，tscale用于平衡量纲。

Fθt=

(3)

式中：γ为间歇因子；y为到物面的最小距离；δ为边界层厚度；系数ce2=50。由于转捩模型与SA湍流模型耦合，在此模型中Fwake为尾迹区开关函数，取值为1.0。其他项形式为

(4)

式中：Ω为涡量的模；U为当地速度。转捩雷诺数Reθt的值是通过来流湍流度Tu与压力梯度参数λθ值拟合的经验公式求解得到，形式为

(5)

式中：压力梯度参数为

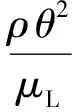
(6)

式中：θ为边界层动量厚度；s为流线的弧长。由于Reθt的经验公式的两端都有未知数θ值，因而通过迭代法求解，迭代步为10步。

1.1.2 间歇因子输运方程

间歇因子用于控制边界层的转捩和边界层的再层流化，用于决定湍流模型中的涡黏性系数。间歇因子输运方程为

(7)

在式(7)中生成项Pγ和耗散项Dγ为

(8)

Dγ=Ca2ρΩFturbγ(ce2γ-1)

(9)

式中：S为平均应变率张量的模；扩散项中的系数为σγ=1.0，源项中系数的分别为Ca1=2.0，Ca2=0.06，ce1=1.0，ce2=50.0；Flength控制转捩区长度；Fonset控制转捩的起始位置。转捩的起始位置由式(10)～式(14)确定：

Fonset=max(Fonset 2-Fonset 3,0)

(10)

(11)

(12)

(13)

(14)

式中：Rev为流动分离处涡雷诺数；Reθc为失稳动量厚度雷诺数；RT为湍流黏性比。在与SA模型耦合的中，Shivaji和James[10]通过一系列来流湍流度Tu小于1%，且仅考虑在自然转捩情况下的平板的数值模拟给出了Reθc及Flength与转捩动量厚度雷诺数的经验公式，形式为

Reθc=(4.45Tu3-5.7Tu2+1.37Tu+

(15)

Flength=0.171Tu2-0.008 3Tu+0.030 6

(16)

1.1.3 分离诱导转捩

流动发生分离造成流动失稳时，流动分离处涡雷诺数Rev迅速增长，并接近3.235倍的Reθ c，根据这个特点Langtry和Menter[9]设计了分离间歇因子γsep和有效间歇因子γeff，具体表达式为

γsep=

(17)

(18)

γeff=max(γsep,γ)

(19)

式中：Fretattch的作用是当黏性比RT较大时，即当流动再附时，使得分离间歇因子γsep的值趋于0。

1.2 γ-Reθt-CF转捩模型

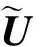
图1 横流流动边界层内速度分布图
Fig.1 Velocity profiles of crossflow boundary layer

Robin等[16]在2015年提出了基于当地变量的对于横流不稳定性引起转捩的判定。在此判定中指定流向的涡量ΩStreamwise值作为边界层中当地横流效应的强度指标，并定义涡量ΩStreamwise为

(20)

(21)

(22)

对涡量ΩStreamwise进行无量纲化，定义无量纲化的横流效应的强度为

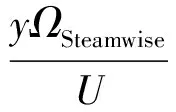
(23)

在转捩动量厚度雷诺数的输运方程中，将横流的影响，以方程中耗散项的形式体现出来，具体公式[16]为

(24)

(25)

(26)

CCrossflow=0.6

(27)

式中：Fθt2项用来限制横流效应的耗散项DSCF的影响范围，使其只能在层流边界层内起作用；ReSCF项为横流修正项，是横流效应的主要项，当横流修正项ReSCF低于转捩的起始位置雷诺数Reθt时起作用。在二维流动中，ReSCF项为一个较大的数值，方程退化为原始的γ-Reθt模型。

通过对NLF(2)-0415后掠翼型在不同后掠角下，不同表面粗糙度下的试验数据和线性稳定性理论的结果，建立横流转捩修正项ReSCF的经验公式。其中，试验数据取自Radeztsky等[17]在1993年完成的NLF(2)-0415后掠翼型的试验；线性稳定性分析则采用eN法。试验中表面粗糙度h分为3个等级，h取不同的值，高度抛光面(Highly Polished)h=0.25 μm，抛光面(Polished)h=0.5 μm和油漆面(Painted)h=3.3 μm。

对于横流引起转捩修正项ReSCF的拟合经验公式为

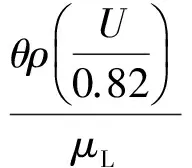
319.51+f(+ΔHCrossflow)-f(-ΔHCrossflow)

(28)

由于ReSCF的经验公式的两端都有未知数θt，在本文中采用牛顿法进行迭代求解。式中f(+ΔHCrossflow)和f(-ΔHCrossflow)是关于ΔHCrossflow的函数。

ΔHCrossflow是表征着横流强度的转换项，具体的计算公式为

(29)

f(+ΔHCrossflow)=6 200(+ΔHCrossflow)+

(30)

+ΔHCrossflow=max(0.106 6-ΔHCrossflow,0)

(31)

(32)

-ΔHCrossflow=

max(-1.0(0.106 6-ΔHCrossflow),0)

(33)

转捩动量厚度雷诺数的输运方程中的其他项及间歇因子输运方程与原始γ-Reθt转捩模型相同。

1.3 γ-Reθt-CF转捩模型与SA湍流模型耦合

(34)

(35)

(36)

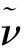
在方程的求解过程中，γ-Reθt-CF中的2个输运方程以及SA模型中的湍流输运方程，均采用有限体积法进行求解，转捩方程和湍流方程均采用松耦合形式与RANS方程结合，时间推进采用广义极小残差(Generalized Minimum RESidual，GMRES)隐式时间格式求解。

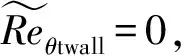
2 算例验证与结果分析

为验证本文所建立的方法的正确性以及考察模型对横流不稳定性引起边界层转捩的预测精度，分别选取NLF(2)-0415后掠翼型和标准6∶1椭球模型作为算例，并将数值模拟的结果与试验值进行比较。

2.1 NLF(2)-0415后掠翼型

该模型试验在亚利桑那州立大学(Arizona State University)的一个低速、低湍流度的风洞中完成。试验模型后掠角为45°，与来流呈-4° 迎角。试验状态：雷诺数为Re=1.9×106～6.5×106；来流湍流度Tu=0.09%。试验中采用萘升华方法测定模型上表面转捩位置。

计算网格如图2所示，u∞为来流速度，翼型弦长c=1.0 m，为保证物面网格y+<1，第1层网格高度为2×10-6m，法向网格增长率为1.1，网格量为300万，远场大约为弦长的20倍，展长为弦长的2.5倍。

选取的计算状态为：马赫数Ma=0.2，雷诺数Re=1.92×106～3.73×106，迎角为固定值α=-4°，远场来流Tu=0.2%，μT/μL=10。

图2 NLF(2)-0415后掠翼型计算网格
Fig.2 Computational grid of NLF(2)-0415 swept airfoil

图3给出了NLF(2)-0415后掠翼型转捩方程变量的残差收敛情况，图中纵坐标为对数坐标，lg(residual)表示对变量的残差取对数。可以看出，当迭代步达到20 000步时，转捩方程的变量残差可以降到10-3～10-4量级之间，此时认为转捩方程计算收敛。

图4给出了在表面粗糙度h=3.3 μm时，原始γ-Reθt模型与γ-Reθt-CF-SA模型数值计算得到的转捩点位置随雷诺数变化曲线及其与试验值和文献中γ-Reθt-CF-SST模型数值计算[12]的对比情况。从图中可以看出，原始γ-Reθt模型在各个雷诺数条件下，预测的转捩起始的位置变化不大，转捩位置均在弦长的80%左右。在Re≤2.19×106时，原始γ-Reθt预测值与试验值吻合较好，但随着雷诺数的增大，横流效应增强，原始γ-Reθt只能预测出由流向T-S波不稳定性引起的转捩，无法预测由横流引起的转捩，因而与试验值相差很大。γ-Reθt-CF-SA模型与γ-Reθt-CF-SST模型预测出的转捩位置，随着雷诺数的增大由71%弦长处提前到15%弦长处，均与试验值吻合较好。

图3 NLF(2)-0415后掠翼型转捩方程残差收敛曲线
Fig.3 Residual history of transition equation of NLF(2)-0415 swept airfoil

图4 转捩点位置随雷诺数变化曲线
Fig.4 Reynolds number effect on transition location

图5和图6给出了在表面粗糙度h=3.3 μm时，雷诺数Re=2.37×106条件下，原始γ-Reθt模型和γ-Reθt-CF-SA模型计算所得的后掠翼型上表面摩擦系数Cf分布与分布云图，从两图中都可以看出，原始γ-Reθt预测的转捩起始位置明显比γ-Reθt-CF-SA模型预测的位置靠前。这是由于在此雷诺数下，横流不稳定性已经成为诱发转捩的主要因素，而原始模型未考虑横流效应对转捩的影响。

图5 NLF(2)-0415后掠翼型上表面摩擦系数分布
Fig.5 Skin friction coefficient distribution on upper surface of NLF(2)-0415 swept airfoil

图6 NLF(2)-0415后掠翼型上表面摩擦系数分布云图
Fig.6 Skin friction contour on upper surface of NLF(2)-0415 swept airfoil

图7给出了在表面粗糙度分别为：高度抛光面(Highly Polished)h=0.25 μm，抛光面(Polished)h=0.5μm和油漆面(Painted)h=3.3 μm条件下，在不同雷诺数下采用γ-Reθt-CF-SA模型计算所得的转捩点的位置与试验值[17-18]的对比。可以看出在各个表面粗糙度条件下，转捩起始位置与试验值都吻合较好。其中，在相同的雷诺数下，随着表面粗糙度的减小，流动越趋于稳定，转捩起始位置越靠后；在相同的表面粗糙度条件下，随着雷诺数的增大，流动中惯性力增强，黏性力减弱，流动趋于不稳定，转捩点位置提前。

图7 不同表面粗糙度时，转捩点位置随雷诺数变化曲线
Fig.7 Reynolds number effect on transition location for different roughness levels

2.2 6∶1标准椭球模型

该模型试验是在德国宇航研究院(DLR)的低速风洞中完成，试验包含多个马赫数、雷诺数和迎角[19]。并且Krimmelbein和Krumbein[20]使用在DLR Tau程序中耦合eN方法也对此模型进行了线性稳定性的分析。两者结果都显示：该模型在雷诺数为Re=6.5×106，马赫数Ma=0.13，迎角为5° 和10° 时，转捩由流向T-S波和横流不稳定性共同影响，而迎角为15° 时，横流不稳定性，成为转捩的主要因素。

计算网格如图8所示，其中，椭球体模型长轴L=1.2 m，为保证物面网格y+<1，第1层网格高度为2×10-6m，法向网格增长率为1.1，网格量为350万，远场大约为长轴的20倍。

计算状态：来流马赫数为Ma=0.13，迎角α=15°，雷诺数为Re=6.5×106，远场湍流条件Tu=0.1%和μT/μL=10。

图9给出了6∶1标准椭球模型转捩方程变量的残差收敛情况，可以看出，当迭代步达到11 500 步时，转捩方程的变量残差可以降到10-4量级左右，此时认为转捩方程计算收敛。

图10分别给出了采用原始γ-Reθt模型与γ-Reθt-CF-SA模型数值模拟得到展开后的椭球表面摩擦系数分布云图。其中，三角形离散点为试验[19]所得的转捩位置，圆形离散点为使用线性稳定性理论计算[20]所得的转捩位置，方形散点为文献[20]中使用γ-Reθt-CF-SST模型计算所得的转捩位置。从图中可以看出，总的来说，γ-Reθt-CF-SA模型与γ-Reθt-CF-SST模型的预测的转捩位置与试验值及线性稳定性理论分析的结果比较相近，且远优于原始γ-Reθt模型的计算结果。但在椭球体的迎风侧θ=0°～50°，没有很好地预测出转捩点的位置，需要对模型进行进一步的修正。

图8 6∶1标准椭球模型计算网格
Fig.8 Computational grid of 6∶1 prolate spheroid standard model

图9 6∶1标准椭球模型转捩方程残差收敛曲线
Fig.9 Residual history of transition equation of 6∶1 prolate spheroid standard model

图11分别给出了椭球体试验[19]得到的、采用原始γ-Reθt模型与γ-Reθt-CF-SA模型数值模拟得到表面摩擦系数分布云图。其中，方形散点为文献[20]中使用γ-Reθt-CF-SST模型计算所得的转捩位置。从图中可以看出，原始γ-Reθt模型预测的转捩区的面积远远小于γ-Reθt-CF-SA模型与γ-Reθt-CF-SST模型，这是由于原始γ-Reθt模型只能预测由T-S波不稳定性引起的转捩，而γ-Reθt-CF-SA 模型与γ-Reθt-CF-SST模型能预测出由T-S波不稳定性和CF波不稳定性共同作用诱导转捩。

图10 椭球模型展开后表面摩擦系数云图
Fig.10 Unwrapped contour plot of skin friction coefficient contour of prolate

图11 椭球模型表面摩擦系数云图(α=150°，Re=6.5×10,Ma=0.13)
Fig.11 Skin friction coefficient contour of prolate (α=150°，Re=6.5×10,Ma=0.13)

3 结 论

将具有横流转捩预测能力的γ-Reθt-CF模型推广到SA湍流模型中，并通过NLF(2)-0415后掠翼型和标准6∶1椭球模型对其进行了算例验证，得出以下结论：

1) SA湍流模型耦合γ-Reθt-CF转捩模型，具备转捩预测的能力，与试验值和线性稳定性理论的值对比，吻合度很好。

2)γ-Reθt-CF-SA转捩模型考虑了三维横流因素以及外形表面粗糙度对转捩的影响，在有横流效应的情况下，预测精度远远高于原始γ-Reθt转捩模型。

3) 通过构造当地横流效应的强度指标，γ-Reθt-CF-SA转捩模型对横流不稳定性引起的转捩判据完全基于当地化变量，因而对复杂几何外形以及现代CFD的大规模并行计算，具有很好的适用性，尤其是将模型引入开源SU2计算流体力学分析平台中，可以为工程外形的转捩预测提供有效的手段。

4)γ-Reθt-CF-SA转捩模型在椭球体的迎风侧预测转捩点的位置与试验值有些差异，这些方面在后续的工作中，还需要做进一步研究。

[1] 朱自强, 吴宗成, 丁举春. 层流流动控制技术及应用[J]. 航空学报, 2011, 32(5): 765-784.

ZHU Z Q, WU Z C, DING J C. Laminar flow control tech-nology and application[J]. Acta Aeronoutica et Astronautica Sinica, 2011, 32(5): 765-784 (in Chinese).

[2] LI X L, FU D X, MA Y W. Direct numerical simulation of hypersonic boundary layer transition over a blunt cone with a small angle of attack[J]. Physics of Fluids, 2010, 22(1): 90-105.

[3] ANTONIOS M, LUCA B, PHIPIPP S.DNS and LES of estimation and control of transition in boundary layers subject[J]. International Journal of Heat and Fluid Flow 2008, 29(2): 841-855.

[4] SU C H, ZHOU H. Transition prediction of a hypersonic boundary layer over a cone at small angle of attack-with the improvement of eNmethod[J]. Science in China Series G: Physics, Mechanics & Astronomy, 2009, 52(1): 115-123.

[5] MICHEL R. Etude de la transition sur les profilsd′aile: Report 1/1578A 192[R]. ONERA, 1952.

[6] MARK D， MICHEL B. Viscous-inviscid analysis of transonic and low reynolds number airfoils[J]. AIAA Journal 1986, 25(10)： 1347-1355.

[7] CODER J G, MAUGHMER M D. A CFD-compatible transition model using an amplification factor transport equation[C]//Grapevine Texas 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Reston: AIAA, 2013.

[8] 王亮， 符松． 一种适用于超音速边界层的湍流转捩模式[J]． 力学学报， 2009, 41(2): 162-168.

WANG L, FU S. A new transition/turbulence model for the flow transition in supersonic boundary layer[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(2): 162-168 (in Chinese).

[9] LANGTRY R B, MENTER F R. Transition modeling for general CFD applications in aeronautics: AIAA-2005-0522[R]. Reston: AIAA, 2005.

[10] SHIVAJI M, JAMES D B. Application of the correlation-basedγ-Reθttransition model to Spalart-Allmaras turbulence model: AIAA-2011-3979[R]. Reston: AIAA， 2011.

[11] JEONG H S, SOO H P. Modeling and prediction of the crossflow transition using transition transport equations: AIAA-2015-3160[R]. Reston: AIAA, 2015.

[12] COMELIA G, ANDREAS K. Extension of theγ-Reθtmodel for prediction of crossflow transition: AIAA-2014-1269[R]. Reston: AIAA, 2014.

[13] MEDIDA S, BAEDER J D.A new crossflow transition onset criterion for RANS turbulence models[C]//Grapevine Texas 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Reston: AIAA, 2013.

[14] SEYFERT C, KRUMBEIN. A correlation-based transition turbulent modeling for three-dimensional aerodynamic configurations: AIAA-2012-0448[R]. Reston: AIAA, 2012.

[15] 徐家宽， 白俊强， 乔磊, 等． 横流不稳定性转捩预测模型[J]. 航空学报, 2015, 36(6): 1814-1822.

XU J K, BAI J Q, QIAO L, et al. Transition model for predicting crossflow instabilities[J]. Acta Aeronoutica et Astronautica Sinica, 2015, 36(6): 1814-1822 (in Chinese).

[16] ROBIN B, LANGTRY, KAUSTAV S, et al. Extending theγ-Reθtlocal correlation based transition model for crossflow effects: AIAA-2015-2474[R]. Reston: AIAA, 2015.

[17] RADEZTSKY R H, REIBERT M S, SARIC W S, et al. Effect of micron-sized roughness on transition in swept-wing flows: AIAA-1993-0076[R]. Reston: AIAA, 1993.

[18] DAGENHART J R, SARIC W S. Crossflow stability and transition experiments in swept-wing flow: TP 1999-209344[R]. Washington, D.C.: NASA, 1999.

[19] KREPLIN H P, VOLLMERS H, MEIER H U. Wall shear stress measurements on an inclined prolate spheroid in the DFVLR 3 m×3 m low speed wind tunnel: Report IB 22-84 A 33[R]. Göttingen: DFVLR-AVA, 1985.

[20] KRIMMELBEIN N, KRUMBEIN A. Automatic transition prediction for three-dimensional configurations with focuson industrial application[J]. AIAA Journal of Aircraft, 2011, 48(6): 1878-1887.

Genevalizationandvalidationofγ-Reθt-CFtransitionmodelingincombinationwithSpalart-Allmarasturbulencemodel

JUShengjun,YANChao*,YEZhifei

SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China

Oneofthemajor3Dtransitionmechanismsistransitionduetocrossflow(CF)instability.Theγ-Reθt-CFtransitionmodelisalocalcorrelation-basedapproachforpredictionoftransitioncausedeitherbyTollmien-Schlichtingsteamwiseinstabilityorcrossflowinstability.Inordertoimprovetheefficiency,γ-Reθt-CF-SAmodeliscoupledwiththeone-equationSpalart-Allmaras(SA)turbulencemodel,andisthenimplementedinopen-sourceStandfordUniversityUnstructured(SU2),aplatformforcomputationalfluiddynamicsanalyses.Inordertovalidateandassesspredictionaccuracyofnewmodel,aseriesoftransitionflowsaresimulatedincludingNLF(2)-0415sweptairfoiland61prolatespheroidstandardmodel.Computationresultsusingγ-Reθt-CF-SAmodelareingoodagreementwithavailableexperimentaldata,farsuperiortothoseusingoriginalγ-Reθtmodel.Modelproposedcaneffectivelypredictlocationofcrossflowinstabilitytransition.

transitionmodel;crossflowinstability;localcorrelation-based;momentumthickness;intermittency

2016-04-28；Revised2016-06-02；Accepted2016-06-25；Publishedonline2016-07-181513

URL：www.cnki.net/kcms/detail/11.1929.V.20160718.1513.002.html

.E-mailyanchao@buaa.edu.cn

2016-04-28；退修日期2016-06-02；录用日期2016-06-25； < class="emphasis_bold">网络出版时间

时间：2016-07-181513

www.cnki.net/kcms/detail/11.1929.V.20160718.1513.002.html

＊

.E-mailyanchao@buaa.edu.cn

鞠胜军， 阎超， 叶志飞．γ-Reθt-CF转捩模型在Spalart-Allmaras湍流模型中的推广及验证J． 航空学报,2017,38(4):120383.JUSJ,YANC,YEZF.Generalizationandvalidationofγ-Reθt-CFtransitionmodelingincombinationwithSpalart-AllmarasturbulencemodelJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):120383.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0205

V221.3

A

1000-6893(2017)04-120383-09

(责任编辑： 鲍亚平， 张晗)