柱形生物质和石英砂传热实验与模拟研究

郭飞宏 王泽宇 仲兆平

(1.东南大学能源与环境学院，南京 210096; 2.能源热转换及其过程测控教育部重点实验室，南京 210096)

柱形生物质和石英砂传热实验与模拟研究

郭飞宏1,2王泽宇1,2仲兆平1,2

(1.东南大学能源与环境学院，南京 210096; 2.能源热转换及其过程测控教育部重点实验室，南京 210096)

从实验和模拟两方面，利用虚拟球元法改进传统的计算流体力学耦合离散单元法(DEM-CFD)，对流化床内的柱形生物质和石英砂的流动传热过程进行了研究。建立了混合流动与传热的实验系统，并进行了模拟和分析，结果表明：双组分颗粒混合指数(MI)经过迅速增加、缓慢增加以及稳定期3个阶段。随着表观气速的增加，颗粒混合指数升高，一定范围内的高气速有利于柱形生物质和石英砂的混合。加热后的柱形生物质和石英砂的初始温度为120℃，流化空气为常温25℃。流化过程中，柱形生物质颗粒温度普遍大于石英砂的温度。当表观气速比较小时，双组分颗粒的混合受到限制，流化床内不同高度的颗粒平均温度差较大；表观气速较大时，流化床颗粒平均温度差不明显。虚拟球元解决了传统DEM-CFD计算模型不适用于大尺寸柱形颗粒系统的问题。对比红外热图像和模拟结果，实验值和模拟结果比较接近，改进的DEM-CFD方法可以较好地模拟柱形生物质和石英砂的流动传热。

柱形生物质； 石英砂； 传热； 实验； 模拟

引言

流化床中的气固流动属于高浓度的流态化过程，具有高强度的热量、质量和动量传递的优点。流化床技术作为生物质热解或直接燃烧的主要技术，其内部流动复杂程度极高，成为气固两相流领域研究的热点。相比实验研究，数值模拟能通过状态参数设置快速方便地反映稠密相流动和传热状态，因此成为研究流化床流动及传热的主要方法之一[1-3]。但由于数值计算方法采用了简化或抽象的模型来模拟真实条件下的流动，其结果需要实验测量进行定性或定量的验证。

TSUJI等[4]提出将DEM和CFD耦合的DEM-CFD方法后，在欧拉-拉格朗日框架中的气固流动模拟计算取得了长足的发展。FENG等[5]基于DEM-CFD对由不同尺寸不同密度组成的双组分颗粒的流化、混合及分离过程进行了模拟。DI RENZO等[6]基于DEM-CFD对流化床中2种具有相同直径但密度不同的双组分颗粒进行了模拟。在传热过程的流化床中，一些研究者也尝试将DEM-CFD方法与传热模型相耦合[7-9]。传统DEM方法只适用于球形颗粒，然而在实际过程中，生物质流化床中不仅仅有规则的球形颗粒，还有很多的异形颗粒，并且尺度都较石英砂大，对于这类问题的模拟，传统的DEM-CFD方法往往无能为力。基于此，研究者对传统的DEM-CFD方法进行了扩展研究，使之能够适用于非球形颗粒流动的模拟[10-11]。

本文从实验和模拟两方面，采用DEM-CFD和虚拟球元法对柱形生物质-石英砂双组分流化床流动及传热进行模型建立、验证。为检验模拟结果的准确性，搭建可视化-透红外流化床实验台，通过分析流化床内颗粒混合指数、颗粒运动和温度分布，以期揭示流化床双组分流动与传热的规律。

1 流动和传热的基本理论

采用虚拟球元法来处理柱形颗粒的受力作用。在气固曳力耦合方面采用改进后的Ergun和Wen & Yu气固曳力模型[12-13]，在气固传热耦合方面采用等效直径法改进传统Gunn对流传热公式。

1.1 改进的气固作用力

气固两相流动中的气相微分方程与单相流相似，但由于单个计算网格内存在固体颗粒，因此必须引入气相空隙率来考虑单位网格内固体所占体积比例的影响。气相连续相方程为

(1)

式中ε——单位网格空隙率，其值等于单位网格内气体所占的体积比例

ρf——气体密度τ——应力张量

uf——气相瞬时速度矢量

将柱形颗粒视为由紧密排列的单一尺寸虚拟小球组成。作为模型参数定义虚拟球的直径为dfic，定义虚拟小球占柱形颗粒的体积分数为afic。这样如果dfic足够小而afic足够大，虚拟小球的聚团就可以被视为大尺寸实心颗粒。则空隙率ε就可以表示为

ε=1-ap-asafic

(2)

式中ap——单位网格内小尺寸颗粒的体积分数

as——单位网格内柱形颗粒的体积分数

气相动量方程为

(3)

其中

(4)

式中p——当地气相平均压力

f——气固曳力

β——气固曳力系数

Np——单个网格内石英砂颗粒个数

Nfic——单个网格内虚拟颗粒的个数

Vp——单个石英砂颗粒体积

Vfic——单个虚拟颗粒体积

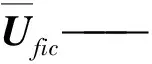
常用的曳力模型有Ergun模型、Wen & Yu模型[14]和Gibilaro模型[15]等。本研究中，根据空隙率的不同分别采用Ergun和Wen & Yu表达式计算，即

(5)

μf——气相粘度Re——雷诺数

CD——流场内单颗粒曳力系数

1.2 改进的气固对流换热

气固对流换热Qf-p受到气固两相温度差和对流传热系数的影响[16-17]，其表达式为

(6)

其中

βT=Nukf/dp

(7)

式中Qf-p——气相与颗粒相对流换热量

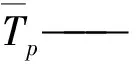
Sp——颗粒表面积Tf——流体温度

βT——对流换热系数

kf——气相导热系数

dp——网格内的颗粒平均直径

Nu——Nusselt数

结合虚拟球元法的思想，把每个气体和柱形生物质的对流换热看成是每个虚拟球元与气体的对流换热。通过直接数值模拟的方法比较，得知采用等效直径和球形度表示的修正Gunn公式在模拟非球形颗粒时具有一定的准确性[18-19]。等效直径方法表达式为

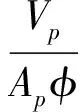
(8)

式中Ap——柱形颗粒的表面积

φ——圆球度，定义为等表面积的球体积与柱形颗粒体积的比值

本研究基于Gunn模型，Nu的计算式为

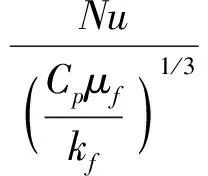
(1.33-2.4ε+1.2ε2)Re0.7

(9)

式中Cp——固体颗粒比热容

2 实验系统及模型建立

2.1 实验系统

生物质与石英砂混合流动与传热实验装置如图1所示。实验装置主要包括流化床主体、供风系统、加热系统、数据采集系统以及图像采集系统。流化空气为常温空气，研究热颗粒(加热后的颗粒)随时间的冷却情况和在流化床内的流动状态。加热后的颗粒初始温度为120℃，流化空气为常温25℃。红外热像仪用来记录颗粒温度随时间的变化情况，高速摄影仪用来记录不同时间点的流动状态。实验测量所得的数据将为后续模拟结果的检验提供依据。

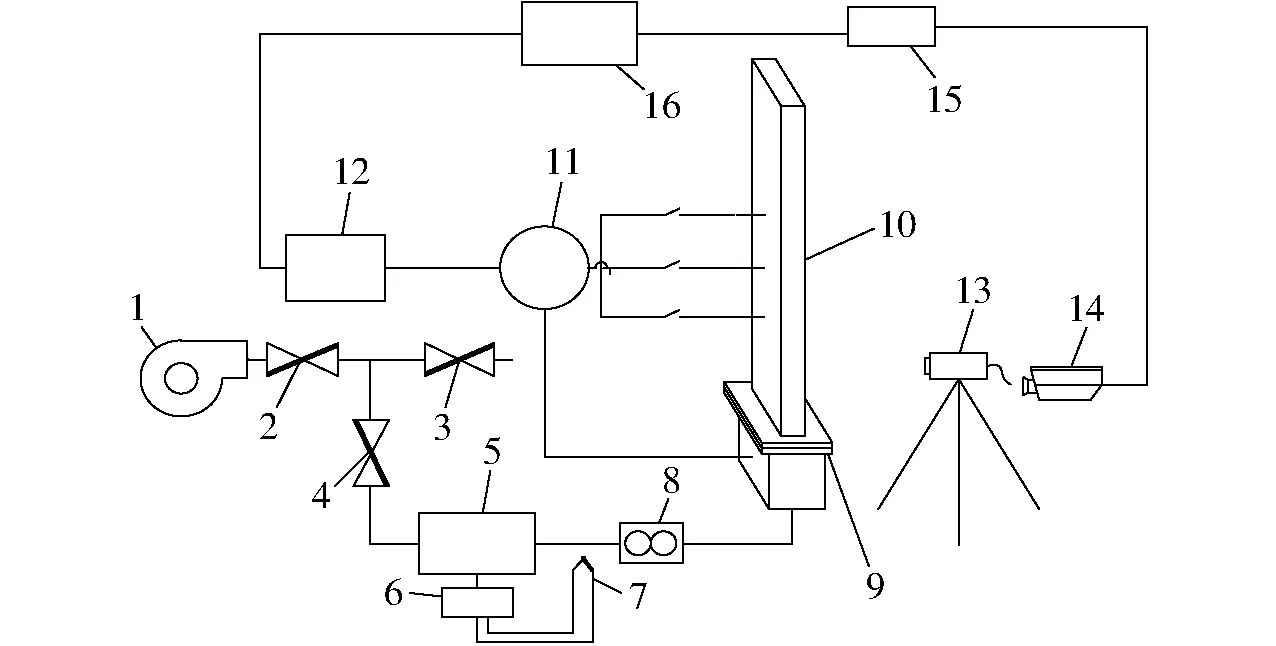
图1 流化床实验系统Fig.1 Schematic diagram of fluidized bed system1.鼓风机 2.总阀 3.放空阀 4.控制阀 5.气体加热器 6.温控箱 7.热电偶 8.转子流量计 9.布风板 10.流化床11.差压变送器 12.USB数据采集器 13.高速摄影仪 14.红外热像仪 15.路由器 16.计算机

按照生物质质量分数计算并取用实验所需的一定数量生物质颗粒，并与石英砂混合后放入电加热炉中加热至颗粒初始温度，保持1～2 h以使柱形生物质颗粒内部温度分布均匀后迅速加入流化床中，同时调节流量计旋钮使表观气速达到工况要求。分别用高速摄影仪和红外热像仪采集流化颗粒流动状态图像和颗粒温度分布。

2.2 实验材料

实验所用物料如表1所示，其中比热容和导热系数为KD2Pro型热特性分析仪(美国DECAGON)测定10个样品的平均值。

表1 实验材料性质Tab.1 Properties of experimental material

2.3 物理模型

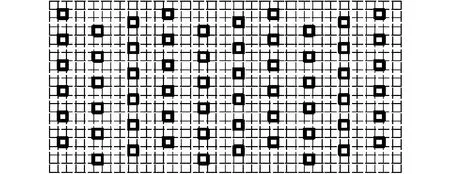
图2 布风板喷口设置Fig.2 Schematic diagram of air distribution plate

初始布置时，石英砂颗粒松散堆积于生物质颗粒下部，柱形颗粒之间、柱形颗粒与石英砂之间存在着一定间隙，在布风板气流进入床内前，颗粒有1 s的时间自由下落成紧密堆积形式。本模拟中布风板开孔布置如图2所示，布风板尺寸为床体截面尺寸(80 mm×40 mm)，共开有60个方形小孔，其开孔率为5%。图中粗实线代表布风板喷口处，其余部分均为平壁面，每个网格尺寸为2 mm×2 mm，上下相邻开孔距离为4 mm，左右相邻两排喷口间距也为4 mm。实践证明如喷口过于接近四周壁面，则会引起计算过程的发散，且会发生床内颗粒超出边界造成计算错误，因此布风板四周靠近壁面处都不设置喷口。模拟计算中，壁面采用无滑移边界条件。入口边界采用速度入口边界条件，布风板上气孔内设置为速度入口边界条件，其余部分为壁面无滑移边界条件。出口边界采用常用的压力出口边界条件。本研究设置初始压力为0 Pa，初始气相速度为0 m/s。

3 实验结果与讨论

3.1 颗粒的混合分析

图3和图4为石英砂和柱形生物质在不同气速不同时刻下的混合情况。可见，柱形生物质主要存在于中上部分的床层区域，在气泡聚并并发生破碎时，一部分被抬高的生物质穿过中间床层的空隙回落到中、低床层中，后又被周围的石英砂抬升至床层顶部，以此往复运动。当表观气速v=1.0 m/s时，颗粒整体膨胀高度较小，此时的柱形生物质主要聚集在流化床的上部，双组分的混合程度不是很好。当表观气速v=1.5 m/s时，颗粒整体膨胀高度较大。t=0.5 s时, 床料被喷口产生的高速气体整体抬升至100 mm的高度。t=2.0 s时,中间位置生成了大而明显的气泡，随即便向上汇合并最终在顶层破裂。t为8、10 s时,气泡破裂，石英砂和生物质开始回落。当表观气速v=2.0 m/s时,柱形颗粒和石英砂的流动更加剧烈，一方面颗粒的上升高度被进一步抬升，另一方面生成更多的气泡，柱形生物质的分布区间更加广泛。

图3 不同气速下流化床内双组分颗粒流动图Fig.3 Flow diagram of binary particles in fluidized bed at different gas velocities

图4 不同时刻流化床内双组分颗粒流动图(v=1.5 m/s)Fig.4 Flow diagram of binary particles in fluidized bed at different time (v=1.5 m/s)

通过双组分颗粒流动图像，分析了流化床流动的混合效果。但在混合过程的中后期，肉眼已经很难辨别混合效果的差距，因此合理准确定量分析混合效果的方法显得尤其必要，Lacey混合指数I[20]能有效克服标准偏差的缺点。其表达式如下

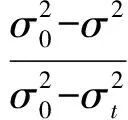
(10)

其中

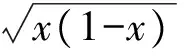
(11)

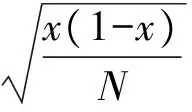
(12)

式中σ——实际混合时的标准差

σ0——完全分离时的标准差

x——某一颗粒在样本中所占的比例

N——取样网格中平均样本数

σt——完全随机混合时的标准差

图5为不同表观气速下颗粒混合指数随时间的变化曲线。可以看出，不同气速下柱形生物质和石英砂的混合指数基本上经历了迅速增加期、缓慢增加期以及稳定期3个阶段。v=1.0 m/s时，床料混合指数首先在1 s内，由0迅速增至0.4，随后在1～1.5 s的时间内基本维持不变，在1.5～2.0 s内混合指数又迅速增至0.56左右，之后维持在0.56左右。表观气速v=1.5 m/s时，0～1.0 s为混合指数的迅速增加期，I从0增至了0.60，随后在1.5～2.0 s内进入到了缓慢增加期，在2.0～3.0 s内混合指数在0.64左右上下波动。v=2.0 m/s时，混合指数数值明显比较高，最终稳定在0.72左右。不同表观气速下，由混合指数变化规律可知，较高的表观气速有利于柱形生物质和石英砂的混合。

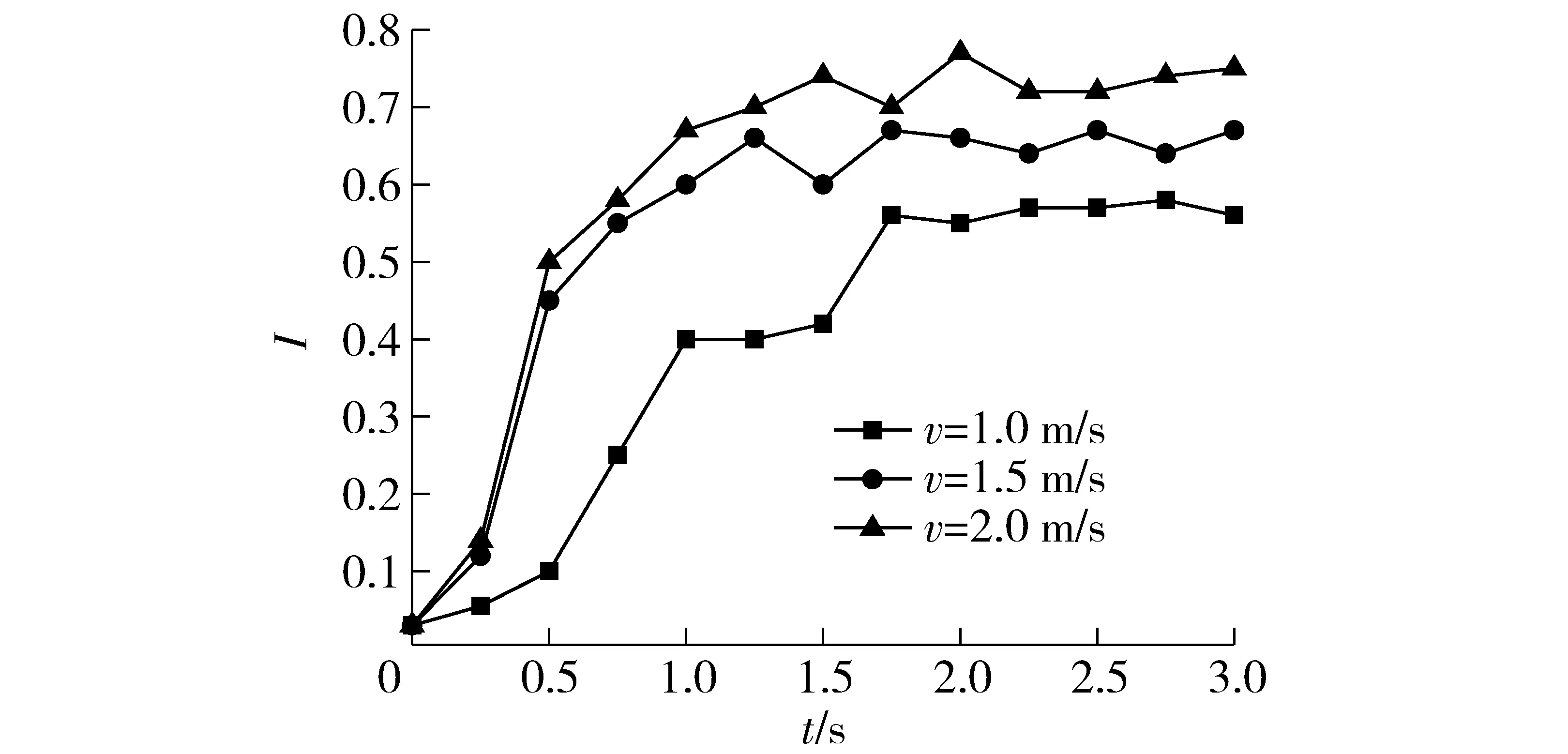
图5 不同气速下混合指数随时间的变化曲线Fig.5 Variation curves of mixing index with time at different gas velocities

3.2 红外热图像温度分析

不同时刻和速度下，生物质质量分数为10%的颗粒热红外温度分布如图6、7所示。由图6可知，当t=1 s时流化床内的颗粒温度分布不太均匀，床层底处的颗粒(h=20 mm)受到常温空气的冷却，温度低于高床层处(h=80 mm)的温度。随着表观气速的增加，这种温度的不均匀性有一定程度的减小。随着时间的增加，颗粒的温度逐渐降低。当t=20 s时，中床层(h=50 mm)的颗粒温度相对较高，这主要是因为柱形生物质主要分布在中床层处，柱形生物质的温度高于石英砂的温度。由于生物质比热较大，且表面传热系数较小，同时也由于单个生物质质量较大，温度下降得较慢。图7中较高的波峰主要是生物质颗粒存在的区域，整体来看，中间床层的温度较高，随着时间的变化，高床层的温度变化较大，中低床层的温度趋于均匀，而低床层的温度普遍低于中间床层的温度。同时，靠近壁面的颗粒温度也偏低。

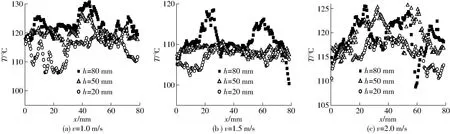
图6 颗粒的热红外温度分布(t=1 s)Fig.6 Infrared temperature distribution of particles (t=1 s)

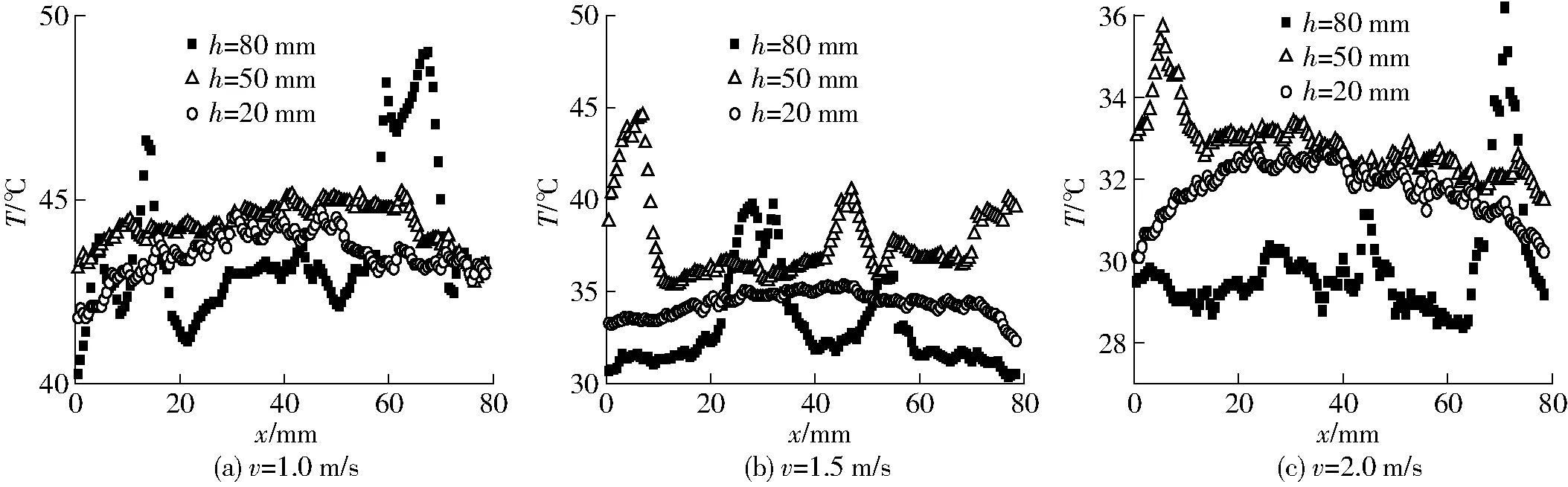
图7 颗粒的热红外温度分布(t=20 s)Fig.7 Infrared temperature distribution of particles (t=20 s)

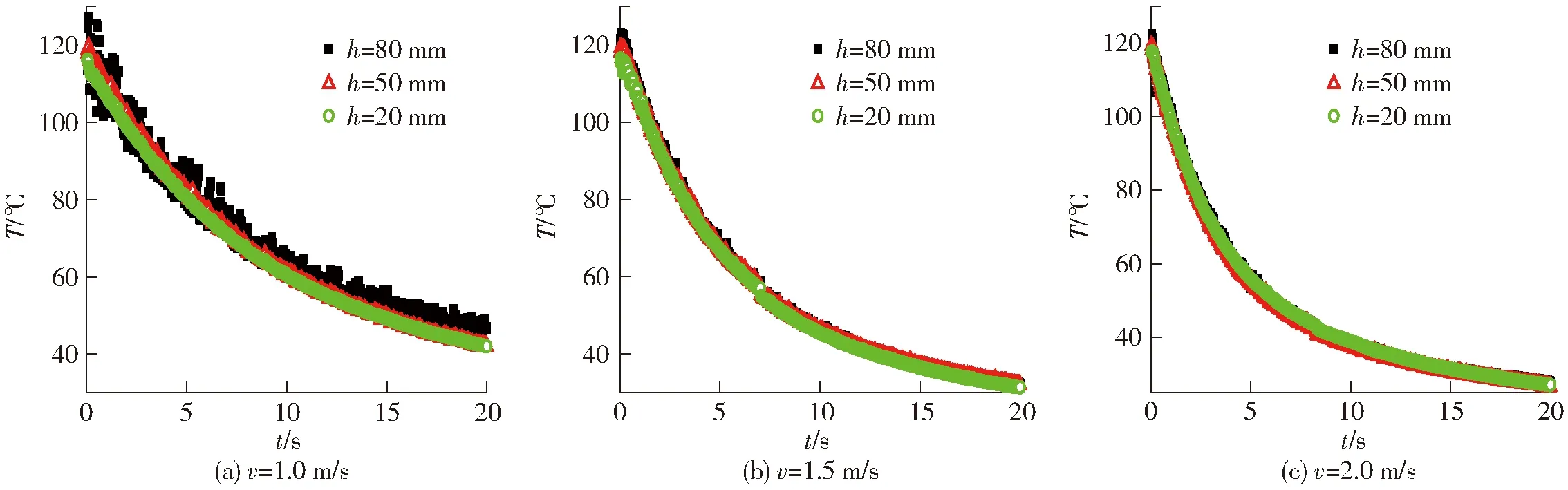
图8 不同气速下颗粒温度随时间的变化曲线Fig.8 Variation curves of particle temperature with time at different gas velocities

图8为生物质质量分数为15%的工况下，不同气速条件下的颗粒平均温度随着时间的变化曲线。流化床内床料温度随着时间的推移，下降速度逐渐降低。表观气速对流化床温度的影响较为明显。由图8可以看出当表观气速为1.0、1.5、2.0 m/s时，床内流化开始后0～3 s的时间内床料平均温度从120℃分别下降到了95℃、83℃、73℃；床内流化开始后0～20 s的时间内床料平均温度分别下降到了42℃、33℃、29℃。可见，当表观气速比较大时，流化床内的颗粒平均温度降幅比较大。当v=1.0 m/s时，床内生物质与石英砂混合情况并不理想，导致大部分生物质颗粒在最高床层区域运动，在平均温度趋势图中则表现为：高床层区域的颗粒平均温度明显高于其他2个床层高度下的颗粒平均温度，并且平均温度产生较大幅度的震荡。t=20 s，v=1.0 m/s时，h=80 mm处的颗粒平均温度为50℃，比其他床层高度的颗粒平均温度高5～8℃，这说明生物质颗粒的冷却速度明显小于石英砂颗粒。而v=1.5 m/s和v=2.0 m/s时，由于床内气泡数量较多，尺寸较大，生物质能够充分与气泡接触，床内物料混合较剧烈，使得各床层高度下的床料温差并不明显。

3.3 模拟值和实验值的对比

图9、10给出了不同表观气速下，颗粒温度和位置分布随时间变化的模拟情况。从床层高度、床内颗粒和气泡运动状态等方面，对比模拟结果与高速摄影仪拍摄的颗粒瞬时运动状态图像，可以看出模拟结果与实际工况具有一定的相似度。当v=1.5 m/s和v=2.0 m/s时，床内产生了较为强烈的气固换热，由于布风板喷口处气体温度较低，床层底部区域颗粒温度较低，床层中间低温气泡周围的也存在着少量低温石英砂颗粒。由于柱形生物质具有大尺寸、大比热、低导热率等特点，温度下降缓慢，总体上柱形生物质温度比石英砂更高。当t=0.5 s时床内生物质颗粒均在125℃，大部分石英砂的温度也在120～125℃之间，但靠近壁面处的石英砂颗粒温度较低，在105～115℃之间，布风板上部的颗粒温度在105～110℃之间。当时间进行到2 s时，床料被抬升至150 mm高度。柱形生物质温度下降至100～110℃，床内石英砂降为95℃左右，壁面处的石英砂温度为85～90℃。当t=10 s时，床料温度下降至25～40℃之间，生物质温度较大，在50～60℃之间。气速较高时，温度下降的趋势更加明显。

图11和图12为表观气速v=1.5、2.0 m/s时不同床层高度颗粒平均温度随时间变化的实验值和模拟值变化曲线。实验过程中，由于双组分颗粒的混合作用，颗粒平均温度会在较短时间内上下波动，但整体呈现下降的趋势，且温度下降的速度随时间的增加而逐渐减缓。模拟时，当表观气速v=1.5 m/s时，经过8 s后，颗粒平均温度从120℃下降至50℃左右，其中颗粒(h=40 mm, 60 mm)的平均温度比较接近，而颗粒(h=15 mm)平均温度比其他位置的温度低3℃左右。当表观气速v=2.0 m/s时，4 s后颗粒平均温度从120℃下降到了80℃左右。与红外热像仪采集的数据比较，在t=4、8 s和v=1.5 m/s、2.0 m/s下，模拟值与实验值的偏差都在10%以内，模拟效果较好。但模拟值相对于实验值，波动更加明显。这是为了缩短模拟过程的计算时间，避免计算程序发散，在模拟工况下石英砂颗粒直径设为0.8 mm，数量最多为20万个，而在实验中石英砂颗粒粒径为0.5 mm。因此实验中的石英砂颗粒数量多于模拟程序中的石英砂颗粒，而作为流化介质，石英砂颗粒数量越多，床内的颗粒接触传热就越充分，温度分布就越均匀。

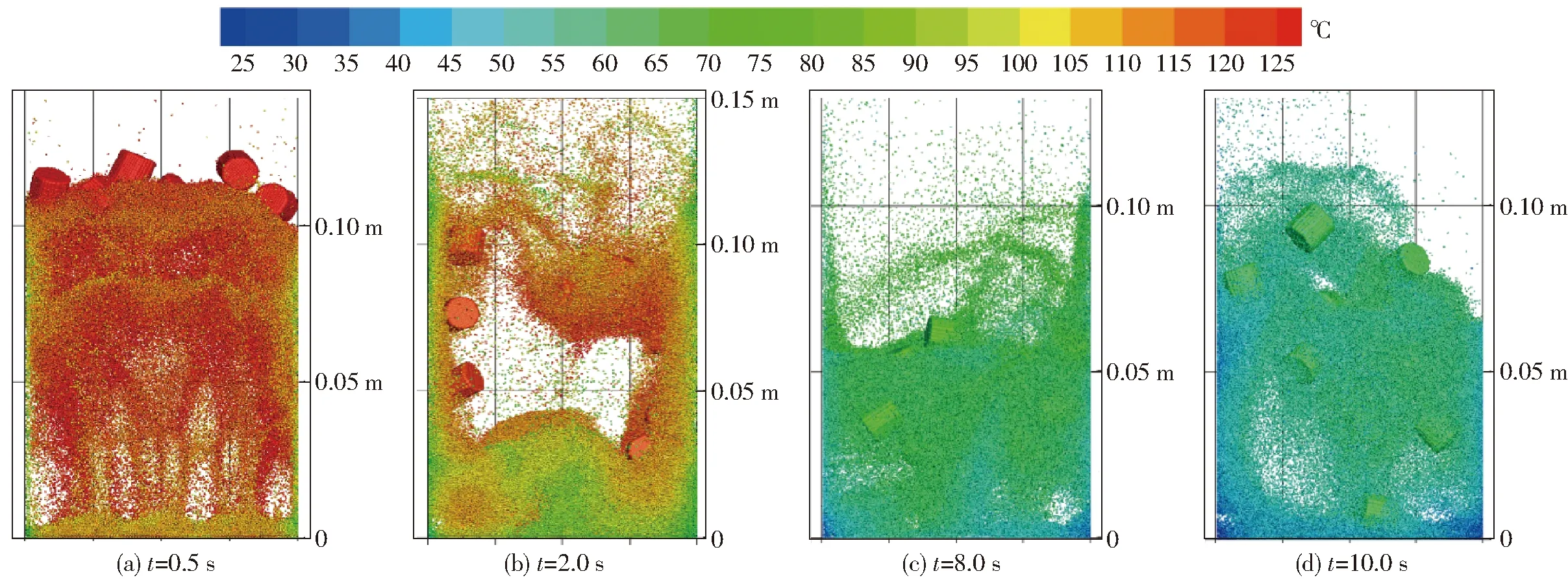
图9 颗粒位置及温度分布随时间的变化 (v=1.5 m/s)Fig.9 Variation of particle position and temperature distribution with time (v=1.5 m/s)

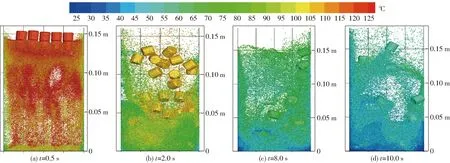
图10 颗粒位置及温度分布随时间的变化 (v=2.0 m/s)Fig.10 Variation of particle position and temperature distribution with time (v=2.0 m/s)

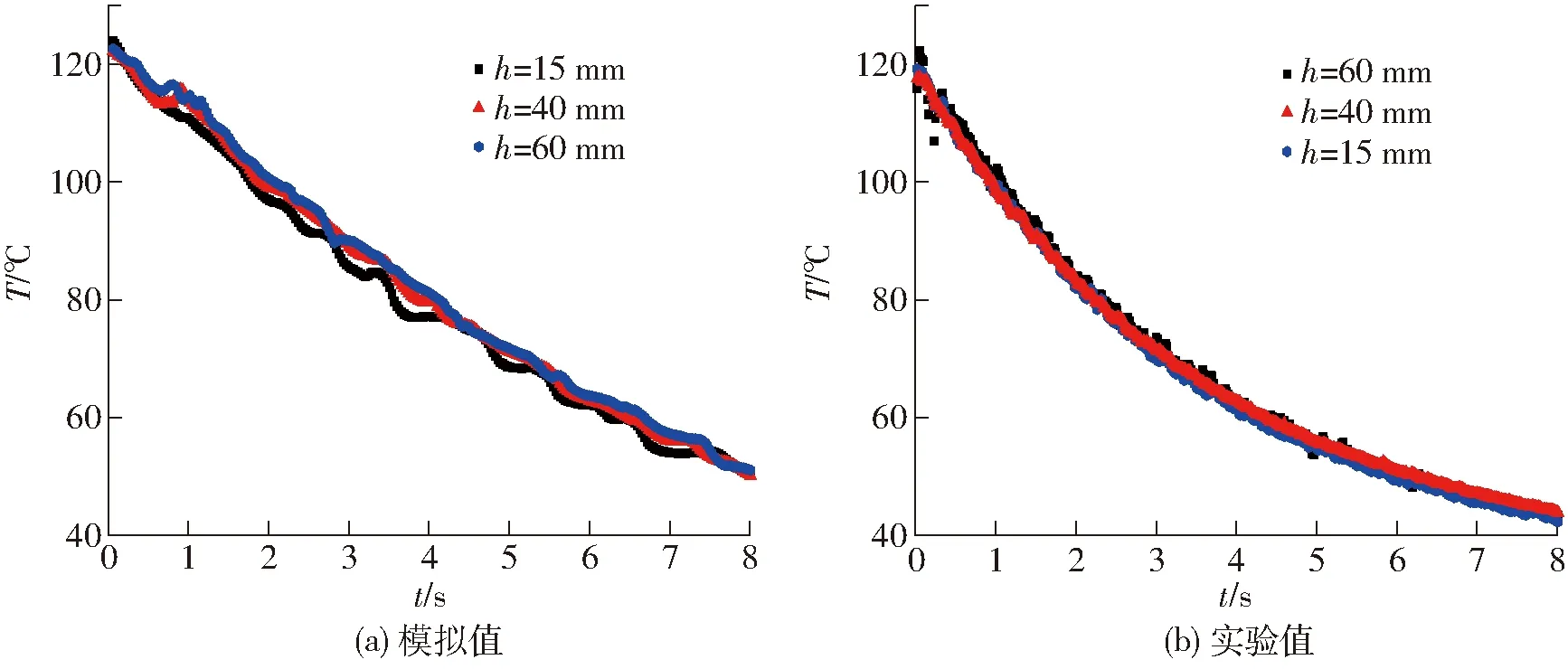
图11 不同床层高度颗粒平均温度随时间的变化(v=1.5 m/s)Fig.11 Variations of average particle temperature at different bed heights (v=1.5 m/s)

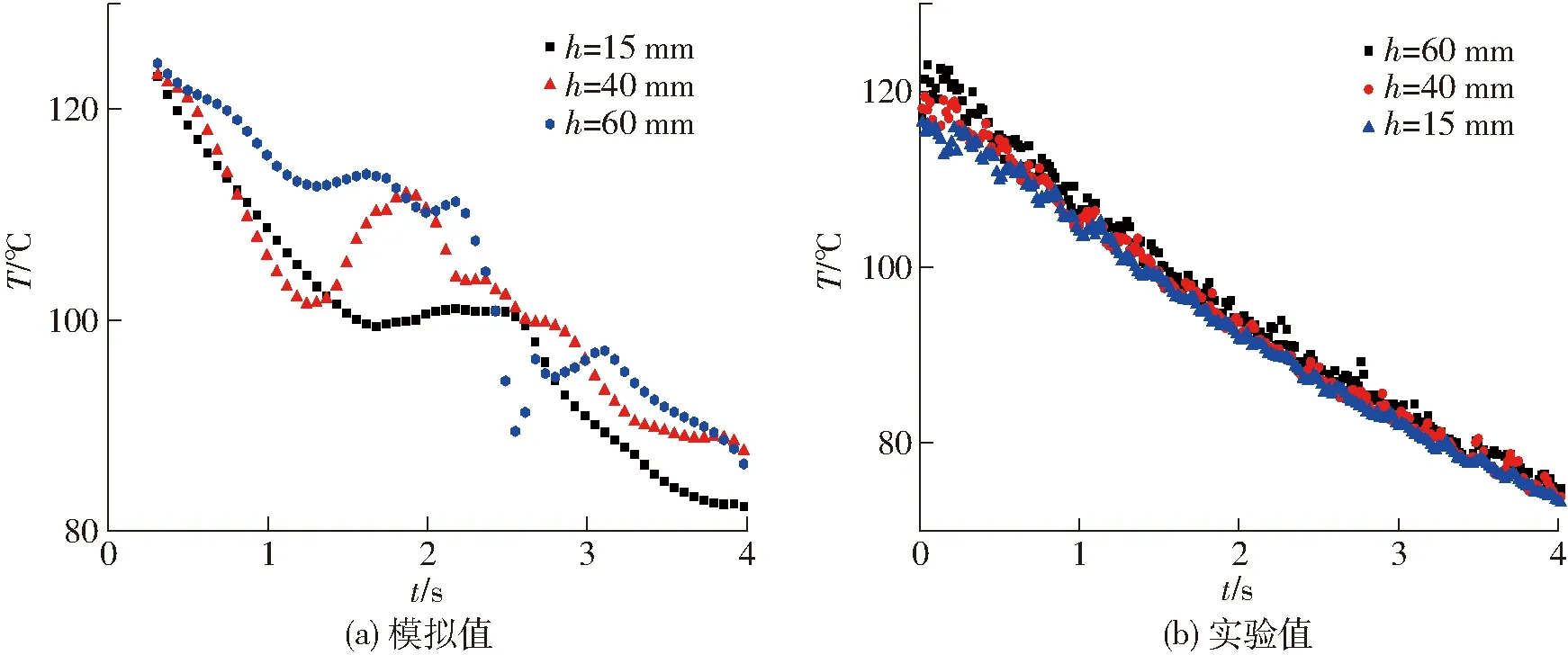
图12 不同床层高度颗粒平均温度随时间的变化(v=2.0 m/s)Fig.12 Variations of average particle temperature at different bed heights (v=2.0 m/s)

4 结论

(1)采用混合指数定量分析了柱形生物质和石英砂在流化床中的混合情况，混合指数经过了迅速增加期、缓慢增加期以及稳定期3个阶段。随着表观气速的增加，混合指数升高，高气速工况有利于柱形生物质和石英砂的混合。

(2)柱形生物质颗粒温度普遍大于石英砂的温度。当表观气速比较小时，双组分颗粒的混合受到限制，流化床内不同高度的颗粒平均温度差较大；表观气速较大时，流化床各高度下的颗粒平均温度差并不明显。

(3)模拟时，柱形生物质的温度降幅小于石英砂，壁面处的颗粒温度也较小。实验值和模拟值比较接近，改进的DEM-CFD方法可以较好地模拟柱形生物质和石英砂的流动传热。

1 郭雪岩,柴辉生,晁东海.大颗粒流化床传热数值模拟与气固传热模型比较[J].上海理工大学学报, 2012, 34(1): 81-87.

2 李洪昌,李耀明,唐忠.风筛式清选装置振动筛上物料运动CFD-DEM数值模拟[J/OL].农业机械学报, 2012, 43(2):79-84.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20120217&journal_id=jcsam.DOI：10.6041/j.issn.1000-1298.2012.02.017.

LI Hongchang, LI Yaoming, TANG Zhong.Numerical simulation of material motion on vibrating screen of air-and-screen cleaning device based on CFD-DEM [J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(2): 79-84.(in Chinese)

3 王维,王璐瑶,许英梅.流化床氛围下多孔物料干燥传热传质的数值模拟[J].化工学报,2012,63(4): 1044-1049.

WANG Wei, WANG Luyao, XU Yingmei.Numerical simulation on porous material drying with fluidized bed [J].CIESC Journal, 2012, 63(4): 1044-1049.(in Chinese)

4 TSUJI Y, KAWAGUCHI T, TANAKA T.Discrete particle simulation of two-dimensional fluidized bed[J].Powder Technology, 1993, 77(1): 79-87.

5 FENG Y, XU B, ZHANG S, et al.Discrete particle simulation of gas fluidization of particle mixtures[J].AIchE Journal, 2004, 50(8): 1713-1728.

6 DI RENZO A, DI MAIO F P, GIRIMONTE R, et al.DEM simulation of the mixing equilibrium in fluidized beds of two solids differing in density [J].Powder Technology, 2008, 184(2): 214-223.

7 ZHOU Z, YU A, ZULLI P.Particle scale study of heat transfer in packed and bubbling fluidized beds[J].AIchE Journal, 2009, 55(4): 868-884.

8 郭飞宏,王泽宇,仲兆平.基于球元重建与大涡模拟耦合并行算法的数值模拟[J].东南大学学报:自然科学版,2017,47(2):283-290.

GUO Feihong, WANG Zeyu, ZHONG Zhaoping.Numerical simulation based on sphere reconstruction and large eddy simulation coupled parallel algorithm [J].Journal of Southeast University:Natural Science Edition, 2017, 47(2):283-290.(in Chinese)

9 刘安源, 刘石.流化床内颗粒碰撞传热的理论研究[J].中国电机工程学报, 2003, 23(3): 161-165.

LIU Anyuan, LIU Shi.Theoretical study on impact heat transfer between particles in fluidized bed [J].Proceedings of the Chinese Society for Electrical Engineering, 2003, 23(3): 161-165.(in Chinese)

10 REN B, ZHONG W Q, CHEN Y, et al.CFD-DEM simulation of spouting of corn-shaped particles[J].Particuology, 2012, 10(5): 562-572.

11 ZHONG W Q, ZHANG Y, JIN B S, et al.Discrete element method simulation of cylinder-shaped particle flow in a gas-solid fluidized bed [J].Chemical Engineering & Technology, 2009, 32(3): 386-391.

12 ILIUTA I, LARACHI F, GRANDJEAN B.Pressure drop and liquid holdup in trickle flow reactors: improved Ergun constants and slip correlations for the slit model [J].Industrial & Engineering Chemistry Research, 1998, 37(12): 4542-4550.

13 MIANOWSKI A, RADKO T, SIUDYGA T.The reactivity of cokes in Boudouard-Bell reactions in the context of an Ergun model [J].Journal of Thermal Analysis and Calorimetry, 2015, 122(2): 1013-1021.

14 NIVEN R K.Physical insight into the Ergun and Wen & Yu equations for fluid flow in packed and fluidized beds [J].Chemical Engineering Science, 2002, 57(3): 527-534.

15 LETTIERI P, BRANDANI S, YATES J G, et al.A generalization of the Foscolo and Gibilaro particle-bed model to predict the fluid bed stability of some fresh FCC catalysts at elevated temperatures [J].Chemical Engineering Science, 2001, 56(18): 5401-5412.

16 ZHAO Y, JIANG M, LIU Y, et al.Particle-scale simulation of the flow and heat transfer behaviors in fluidized bed with immersed tube[J].AIchE Journal, 2009, 55(12): 3109-3124.

17 DI MAIO F P, DI RENZO A, TREVISAN D.Comparison of heat transfer models in DEM-CFD simulations of fluidized beds with an immersed probe [J].Powder Technology, 2009, 193(3): 257-265.

18 TAVASSOLI H，EAJF P，JAM K.Direct numerical simulation of fluid-particle heat transfer in fixed random arrays of non-spherical particles[J].Chemical Engineering Science, 2015, 129: 42-48.

19 FOTOVAT F, ANSART R, HEMATI M, et al.Sand-assisted fluidization of large cylindrical and spherical biomass particles: experiments and simulation[J].Chemical Engineering Science, 2015, 126: 543-559.

20 李少华，朱明亮，张立栋，等.回转装置内三组元颗粒径向混合评价方法分析[J].化工进展, 2013(6): 1224-1229.

LI Shaohua，ZHU Mingliang，ZHANG Lidong, et al.Analysis of three-component radial mixing evaluation methods in rotary retorting [J].Chemical Industry and Engineering Progress, 2013(6): 1224-1229.(in Chinese)

ExperimentandImprovedSimulationonHeatTransferforCylindricalBiomassandQuartzSand

GUO Feihong1,2WANG Zeyu1,2ZHONG Zhaoping1,2

(1.SchoolofEnergyandEnvironment,SoutheastUniversity,Nanjing210096,China2.KeyLaboratoryofEnergyThermalConversionandControl,MinistryofEducation,Nanjing210096,China)

From the two aspects of experiment and simulation, virtual spherical method was used to improve the numerical simulation of the traditional computational fluid dynamics coupling discrete element method (CFD-DEM).The cylindrical particle was regarded as aggregation of small virtual ball, and particle volume factor concept was also introduced to amend the gas-solid force.The gas force acting on the cylindrical particle was calculated through the calculation between gas phase and virtual sphere.The experimental system of flow and heat transfer was established, and the simulation and comparative analysis were also carried out.The mixing index (MI) of the special binary particles was followed by three stages: rapid increase, slow increase and stable phase.With the increase of superficial gas velocity, the mixing index of particles was increased, and the higher gas velocity was favorable for the mixing of the cylindrical biomass and quartz sand.In the experiment of heat transfer, the temperature of cylindrical biomass particles was generally higher than that of quartz sand.When the superficial gas velocity was small, the fluidization of particles was restricted, and the average temperature difference at different heights of fluidized bed was larger.At large gas velocity, the average temperature difference was not obvious.The fictitious element method was employed to solve the incompatibility of the traditional DEM-CFD model.Compared with the infrared thermal images and the simulation results, they were very close and the improved DEM-CFD method can simulate the flow and heat transfer of cylindrical biomass and quartz sand.

cylindrical biomass; quartz sand; heat transfer; experiment; simulation

10.6041/j.issn.1000-1298.2017.10.034

TK6

A

1000-1298(2017)10-0272-08

2017-01-15

2017-03-15

国家自然科学基金项目(U13161115、51276040)和东南大学优秀博士学位论文培育基金项目(YBJJ1644)

郭飞宏(1986—)，男，博士生，主要从事生物质与煤的混合燃烧及模拟研究，E-mail: kerry151@126.com

仲兆平(1965—)，男，教授，博士生导师，主要从事固体废弃物利用研究，E-mail: zzhong@seu.edu.cn