熔融度对熔锥型光纤耦合器特性影响研究

刘 伟，欧阳鑫

（昆明理工大学 智能测控研究所，云南 昆明 650500）

熔融度对熔锥型光纤耦合器特性影响研究

刘 伟，欧阳鑫

（昆明理工大学 智能测控研究所，云南 昆明 650500）

光纤耦合器是现代光纤器件的一个主要部分，熔融拉锥方法是目前制造光纤耦合器应用最广的方法。熔锥型光纤耦合器在制作过程中受到很多种因素影响，文本主要研究熔融度对熔锥型光纤耦合器分特性的影响研究。本文选用合适的连续函数描述了熔锥型光纤耦合器在制作过程中锥形区的渐变特性和熔融度的关系，并建立熔融性光纤耦合器的结构模型。利用数值模拟的方法，讨论了光纤耦合器在不同的熔融度情况下，分光比、插入损耗、附加损耗的变化情况。得出熔融性光纤耦合器的分光比随熔融度周期变化，对于同一种光纤耦合器，周期随着熔融度增加而越来越小。对于不同光纤耦合器，随着光纤耦合器的长度减小，每个周期的长度增加。这对生产中控制光纤耦合器分光比提供了重要的理论依据。

光纤耦合器；熔融拉锥；熔融度；分光比；数值模拟

0 引言

光纤耦合器是光网络和光传感系统中实现光信号分路和合路的重要器件。光纤耦合器主要是完成传输、耦合、分光以及波分复用等功能。在光纤通信、光纤传感和光纤测量中有着重要的应用。从耦合模提出至今，国内外在光纤耦合方面进行了很多理论研究，为光纤耦合器的发展和制造提供了拓实的理论基础。光纤耦合器根据制造方法的不同可以分为三类：腐蚀法、抛磨法以及熔融拉锥法。腐蚀法和抛磨法是最开始用的两种办法，熔融拉锥法具有损耗性低、方向性好和适于批量生产等优势，在耦合器的生产中普遍采用这种方法[1-2]。

熔锥型光纤耦合器在制作过程中，将两根光纤并在一起并对耦合部分进行加热，在熔融过程中进行拉伸。[3-4]由此过程，我们首先选用了合适的连续函数来描述熔锥型光纤耦合器在制作过程中锥形区的渐变特性和熔融度的关系，然后运用了数值计算的方法进行仿真。得出了在不同锥形区、熔融区长度下光纤耦合器的分光比随着熔融度的变化曲线，了解了制作过程中各变量之间的关系[5-8]。

1 模型建立

熔锥型光纤耦合器的功率耦合不仅取决于两光纤中的各自的模场特性，同时也取决与它们的几何形状和相互位置。几何形状包括锥形区和熔融区，相互位置主要由两根光纤的融合度决定。制作熔锥型光纤耦合器第一步将两根光纤去除涂覆层，然后以一定的方式靠拢，最后在高温下加热熔融，同时向两侧拉伸，最终使两根光纤产生一段哑铃型的双向圆锥结构[9-12]。单根熔锥光纤的几何结构如图 1所示，在锥形区，其横截面成指数变换模式。在熔融区，其形状保持不变。

图1 单根光纤拉锥结构图Fig.1 Single fiber pull cone structure

2×2熔锥型光纤耦合器由上述两平行熔锥光纤相互重叠组成的复合波导，其横截面如图2所示：

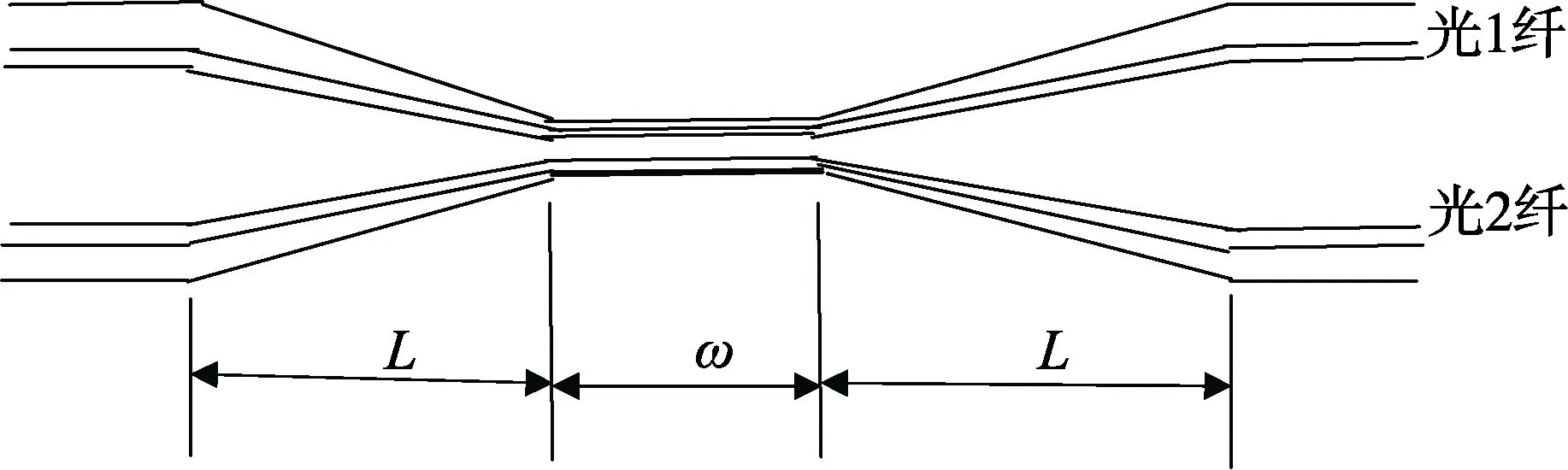
图2 2×2熔锥型光纤耦合器结构图Fig.2 Design of 2×2 fused cone fiber coupler

对于单根光纤在熔融拉锥过程中，根据光纤体积守恒得出纤芯直径、包层直径与拉伸长度之间的关系。我们用L表示单侧拉伸长度，ω表示耦合区长度。纤芯初始直径为a0，包层初始直径为ba。

2×2熔锥型光纤耦合器每根光纤的尺寸同样适用以上公式，同时用d来表示两根光纤之间的距离。在制作过程中，我们用熔融度来表示两根光纤之间的融合程度，其定义为：

当α=0的时，d=a0，此时两根光纤刚好相切。当α=1时，两根光纤最大程度融合，此时d=

2 模型仿真与分析

耦合模理论的提出在初期解决了一些光纤耦合器问题，但根据实际需求，一些数值分析方法被提出并逐步发展完善，数值模拟在光纤耦合器的研究中有着关键的作用，常见的数值分析方法有：有效折射率法、有限元法、光束传播法等。本文主要利用光束传播法（BMP）和有限元法对模型进行仿真分析。

根据实际生产中对光纤参数的要求，我们选用了三组不同参数的光纤耦合器进行仿真分析。第一组选用光纤的包层直径 b0= 1 25μm，纤芯直径a0= 8 .5μm，包层折射率 nc0=1.4633，纤芯折射率nc1=1.4633，入射波长 1330μm，锥形区长度L=20000，熔融区长度ω=12000。第二组选用光纤的包层直径 b0= 1 25μm，纤芯直径 a0= 8 .5μm，包层折射率 nc0=1.4633，纤芯折射率 nc1=1.4633，入射波长 1330μm，锥形区长度 L=16000，熔融区长度ω=10000。第三组选用的包层包层直径 b0= 1 25μm，纤芯直径 a0= 8 .5μm ，包层折射率 nc0=1.4633，纤芯折射率 nc1=1.4633，入射波长1330 μm，锥形区长度L=12000，熔融区长度ω=8000。第二组选用的包层直径包层直径，纤芯直径，包层折射率，纤芯折射率，锥形区长度L=12000，熔融区长度ω=8000。对这三组光纤耦合器记录在不同的熔融度情况下分光比的变化。分光比作为耦合器最重要的参数，其表达式为：

经过仿真得到部分数据表如表1所示。

通过对表1中三种不同规格的光纤耦合器数据分析，得到：对于第一组仿真，分光比为 50/50情况下的耦合效果如图所示，此时熔融度为α=0.6965。

表1 光纤耦合器分光比变化表Tab.1 Optical fiber coupler splitting ratio change table

如图3所示，蓝色线表示直通臂输出功率，绿色表示耦合臂输出功率。在最终输出的时候两根能量完全重合，所以分光比刚好为50/50。同时此光纤耦合器其他性能进行分析：得到插入损耗为3.2 dB，3.2 dB，此插入损耗远小于3 dB，说明此附加损耗：

图3 20000*12000光纤耦合器仿真图Fig.3 Simulation of 20000*12000 fiber coupler

附加损耗值(dB)=

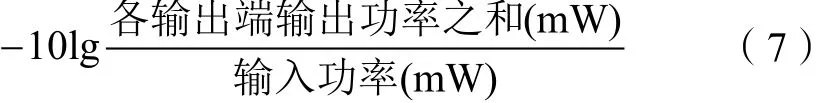
得到附加损耗为0.196 dB。

通过选取不同的熔融度α，计算其对应的分光比，观察两者变化，得到曲线如图4所示。

图4 20000*12000光纤耦合器分光比-熔融度曲线Fig.4 Split Ratio-Melting Curve of 20000*12000 fiber coupler

图中可以看出直通臂输出功率与耦合臂输出功率呈周期性变化，在熔融度为 0.125的时候，几乎所有能量都耦合到耦合臂中，此时分光比为 1/99，随后耦合臂能量减少，直通臂能量增加，在熔融度为0.3225的时候，两根光纤的耦合臂能量相等，此时的分光比为50/50。接着耦合臂能量减少，直通臂能量增加，当熔融度为0.46的时候，能量集中在直通臂，此时的分光比为99/1。熔融度从0.125到0.46，耦合臂和直通臂完成一个周期的耦合。最后两根光纤又一次进行交替变化。

对于第二组仿真，分光比为 50/50情况下的耦合效果如图所示，此时熔融度为α=0.0775。

图5 16000*10000光纤耦合器仿真图Fig.5 Simulation of 16000*10000 fiber coupler

如图5所示，蓝色线表示直通臂输出功率，绿色表示耦合臂输出功率。在最终输出的时候两根能量完全重合，所以分光比刚好为50/50。同时此光纤耦合器其他性能进行分析：得到附加损耗为0.196 dB得到插入损耗为3.2 dB，3.2 dB，满足标准3 dB光纤耦合器要求。

通过选取不同的熔融度α，计算其对应的分光比，观察两者变化，得到曲线如图6所示。

图6 16000*10000光纤耦合器分光比-熔融度曲线Fig.6 Split Ratio-Melting Curve of 16000*10000 fiber coupler

图6中可以看出直通臂输出功率与耦合臂输出功率呈周期性变化，在熔融度为 0.4的时候，能量完全耦合到耦合臂，此时的分光比为 1/99。当熔融度为0.53的时候两根光纤的耦合臂相等，这时分光比再次达到 50/50。当熔融度为 0.65的时候没有能力耦合到耦合臂此时分光比为 99/1。之后两根光纤又一次进行交替变化。

对于第三组仿真，其分光比在1/99情况下的效果如图所示，此时熔融度α=0.6。

图7 14000*10000光纤耦合器仿真图Fig.7 Simulation of 12000*8000 fiber coupler

如图7所示，蓝色线表示直通臂输出功率，绿色表示耦合臂输出功率。在最终输出的时候能量集中在耦合臂中，分光比为 1/99。同时此光纤耦合器其他性能进行分析：插入损耗为0.17 dB，附加损耗为14.15 dB，0.35 dB。

通过选取不同的熔融度α，计算其对应的分光比，观察两者变化，得到如曲线如图8所示。

图8 12000*8000光纤耦合器分光比-熔融度曲线Fig.8 Split Ratio-Melting Curve of 12000*8000 fiber coupler

图中可以看出直通臂输出功率与耦合臂输出功率呈周期性变化，在熔融度为 0.4的时候，两根光纤的耦合臂能量相等，此时的分光比为50/50。当熔融度为0.65的时候，几乎所有能量都耦合到耦合臂中，此时分光比为 1/99。之后耦合臂的能量减少，直通臂的能量增多，在熔融度达到0.85的时候，能量集中在直通臂，此时的分光比为 99/1。最后两根光纤又一次进行交替变化。

3 结果分析与结论

结合实际和仿真结果表明，在光纤包层直径、纤芯直径、包层折射率、纤芯折射率等参数一致情况下，熔锥型光纤耦合器的分光比与拉锥过程中两光纤的熔融度相关。熔锥型光纤耦合器的分光比随熔融度呈周期性变化，且随着熔融度的增加，周期越来越小。并对三种情况进行横向比较，锥形区和熔融区的长度决定了在熔融度0到1之间周期的数量。锥形区和熔融区越长，周期的数量就越多。

在实际生产中，通过控制火焰温度和拉伸速度来决定熔融度的大小。要增加熔融度，一般是增加氢气的量提高火焰温度或放慢拉伸速度增加熔融的时间来实现。当锥形区和熔融区的长度较长的时候，分光比变化的一个周期较短，这就使对熔融度的要求在一个较小的范围内。但是为了追求更小的光纤耦合器的尺寸，会将锥形区和熔融区的长度缩小，这就对实现更高的熔融度提出了要求，同时也要满足熔融型光纤耦合器的分光比需求，要保证在熔融度0到1内至少存在一个周期。

[1] Gu B S, Zhang J L. Simple model and experiment for the wavelength-flattened fiber couplers[J]. 光子学报1994, 23(01).

[2] Tekippe V J, Moore D R, Paul D K. Production, performance,and reliability of fused couplers[J]. SPIE 1999, 3666.

[3] 李川, 张以谟, 刘铁根等. 熔锥光纤耦合器的应变研究[J].光电子·激光, 2001, 12(9): 883-885. DOI: 10.3321/j.issn:1005-0086.2001.09.002.

[4] 酆达, 李铮, 唐丹等. 2×2熔锥型单模光纤耦合器的模型[J].光子学报, 2003, 32(11): 1316-1320.

[5] 蒋奇, 胡德波. 倾斜光纤光栅温度及溶液浓度传感特性研究[J]. 新型工业化, 2011, 1(3): 55-62.

[6] 吕品, 刘建业, 张玲, 等. 惯导系统中光纤陀螺误差信号处理技术研究[J]. 新型工业化, 2011, 1(4): 45-51.

[7] 孙杰. 耦合薛定谔模型在光纤传导中的应用[J]. 软件,2016, 37(02): 22-24

[8] 张晓青, 田书榕, 肖芦洋, 等. 基于Simulink的外调制微波光纤延迟线噪声分析[J]. 软件, 2013, 34(1): 79-81

[9] 任建国, 胡永明, 张学亮, 胡正良. 熔锥型单模光纤耦合器的一致性模型[J]. 半导体光电, 2011, (01): 18-23.

[10] Jiang Junzhen, Qiu Yishen. Improved coupled-mode theory of directional couplers[J]. SPIE 2006, 6025.

[11] 易子馗, 段吉安, 苗健宇等. 2×2单模光纤耦合器的改进控制方法[J]. 光通信技术, 2006, 30(1): 55-57. DOI: 10. 3969/j.issn.1002-5561.2006.01.018.

[12] 戴建广, 陈江博, 王丽等. 熔融拉锥型单模光纤光功率比耦合器的研制[J]. 应用激光, 2006, 26(6): 446-448. DOI:10.3969/j.issn.1000-372X.2006.06.023.

Study on the Effect of Melt Degree on the Characteristics of Fused Tapered Fiber Coupler

LIU Wei, OU Yang-xin
(Kunming University of Science and Technology, Intelligent Measurement and Control Institute, Kunming 650500)

Fiber coupler is a major part of modern fiber optic devices, the melting cone is the most widely used method of manufacturing fiber coupler. The melting cone type fiber coupler is influenced by many factors in the production process. The paper mainly studies the influence of the melt degree on the sub-characteristics of the fusion-type fiber coupler. In this paper, the appropriate continuous function is used to describe the relationship between the tapered characteristics and the melting degree of the fused-cone fiber coupler during the fabrication process, and the structural model of the fused fiber coupler is established. Based on the numerical simulation method, the change of splitting ratio, insertion loss and additional loss of fiber coupler under different melting degree is discussed. It is found that the splitting ratio of the fused fiber coupler varies with the degree of melt, and for the same fiber coupler, the period is getting smaller as the melt degree increases. For different fiber couplers, as the length of the fiber coupler decreases, the length of each cycle increases. This provides an important theoretical basis for controlling the splitting ratio of fiber couplers in production.

: Fiber coupler; Melting cone; Melting degree; Splitting ratio; Numerical simulation

TP913.7

A

10.3969/j.issn.1003-6970.2017.10.028

本文著录格式：刘伟，欧阳鑫. 熔融度对熔锥型光纤耦合器特性影响研究[J]. 软件，2017，38（10）：144-148

刘伟(1991-)，男，安徽桐城人，硕士，主要研究方向：信号处理，通信工程；欧阳鑫，男，研究生导师。