反比例函数中的面积计算题解析归类
2017-11-15江苏省徐州市沛县杨屯中学蔡素丽
江苏省徐州市沛县杨屯中学 蔡素丽
反比例函数中的面积计算题解析归类
江苏省徐州市沛县杨屯中学 蔡素丽
反比例函数一直是困扰学生的一大难题,特别是和反比例函数相关的面积计算,更让学生摸不着头脑。新课程标准对反比例函数这部分的学习目标作了明确的要求:(1)结合具体情境体会反比例函数的意义,能根据已知条件确定反比例函数表达式。(2)能画出反比例函数图象,根据图象和表达式探求k>0和k<0时图象的变化情况。(3)能用反比例函数解决简单的实际问题。其中的面积计算是应用中的重中之重。历数近几年各地的中考试卷发现,与反比例函数有关的面积计算越来越受出题者的青睐,现结合自己的教学积累,把有关反比例函数面积计算的题目归类整理如下:
一、数形结合——巧用比例系数k的几何意义
反比例函数比例系数k与图形面积之间的关系是现阶段初中数学的常见考题类型。k的几何意义充分体现了学生对于反比例函数问题理解的深度以及本质的把握度。纵观近几年考题,此类问题一般以选择、填空题型出现。现举例如下:
例1 如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为12,则这个反比例函数的关系式是__________。
【分析】反比例函数图象上一点到两坐标轴之间距离围成的矩形的面积等于该点横纵坐标乘积的绝对值,即|xy|,由此可总结得出该矩形面积即为|k|。实际解题中,要结合图象所在象限,注意k的取值。
【点评】对反比例函数的比例系数k的几何意义的理解,即过函数图象上任意一点分别向x轴、y轴作垂线,与坐标轴围成的矩形的面积是一个定值|k|,理解这一点,解决此类矩形面积问题时将会得心应手。
对于此类k的几何意义的应用,变式题也是五花八门,变化多样,但是掌握本质是解题的关键,以不变应万变。
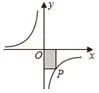
【变式1】如图,点A在双曲线y=上,点B在双曲线y=上,且AB∥x轴,点C和点D在x轴上,若四边形ABCD为矩形,则矩形ABCD的面积为_______ 。
【分析】初看本题,似乎与k的值无法建立联系,但是注意观察可发现,只需延长BA与y轴交于点E,所得两个矩形,即矩形ADOE、矩形BCOE,两矩形面积利用对应反比例函数的k的几何意义即可解决。即S矩形ABCD=S矩形OCBE-S矩形ODAE=3-1=2。
【变式2】如图,反比例函数y=(x>0)的图象上,有点P1、P2、P3、P4,它们的横坐标依次为1、2、3、4。分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1、S2、S3,则S1+S2+S3= _______。
【分析】由题意可知点P1、P2、P3、P4的坐标分别为:(1,2),(2,1),由平移变换,可把S2、S3平移至左侧S1下方,拼成一个矩形,用最左侧矩形面积减去下面空白面积即可。由反比例函数的几何意义可知:
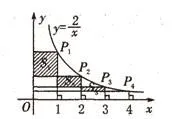
【点评】本题也可以规律题的形式出现,即求S1+S2+S3+…Sn=_______。题目万变不离其宗,解题的关键在于理解k的几何意义及本质特征。
例2 如图,点P是反比例函数y=-象上的一点,PD⊥x轴于D。则△POD的面积为_____________。
【分析】解决反比例函数与三角形面积问题也是常见的k的几何意义的运用。反比例函数图象上的任意一点向一坐标轴作垂线,与坐标原点连线所构成的直角三角形面积是一个定值实际解题中仍需根据图象所在象限,注意k的取值。
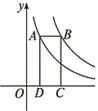
【变式1】如图,在平面直角坐标系中,M为y轴正半轴上一点,过点M的直线l∥x轴,l分别与反比例函数的图象交于A、B两点,若S△AOB=3,则k的值为______ 。
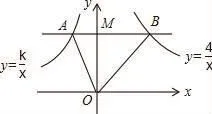
【分析】此题只需两次利用k的几何意义与三角形面积之间的关 系 即 可。 即S△AOB=S△AOM+S△MOB=3,S△MOB=故S△AOM=1,所以k=-2。
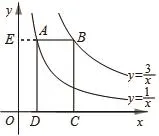
【变式2】如图,点A、B在反比例函数的图象上,过点A、B
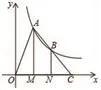
作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
A.4 B.6 C.8 D.12
【分析】本题可利用△BOC的三等分点分得的△BNC的面积是△BOC面积的求出△BON的面积为4,利用k的几何意义求出k=4,故选A。
二、化零为整——妙用反比例函数的对称性
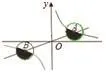
例3 如图,已知函数y1=k1x与反比例函数y2=的图象交于A、B两点(k1>0,k2>0),A点的坐标为(4,2),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分的面积和为_______ 。
【分析】由于反比例函数图象关于原点成中心对称,图中阴影部分的面积和恰好是一个圆的面积,已知两个圆与x轴相切,所以A点的纵坐标即为圆的半径。所以S=4π。
【变式】如图,边长为8的正方形ABCD的对称中心是坐标原点O,AB∥x轴,BC∥y轴,反比例函数y=的图象均与正方形ABCD的边相交,则图中的阴影部分的面积之和为_____ 。
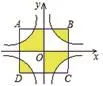
【分析】本题可根据函数表达式,确定两个函数图象之间的关系根据正方形的对称中心是坐标原点,因此,四个小正方形是全等的,反比例函数图象关于原点成中心对称,所以阴影部分面积和是两个小正方形的面积和,故S阴影=×8×8=32。
利用反比例函数的对称性解题,要结合图象的特征,合理利用化零为整的思想解决问题。
三、开拓思维——活用设元法
例4 如图,反比例函数y=(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为_______ 。
【分析】本题可谓逢卷必考,是最受出题者青睐的考题,解决本题可从反比例函数图象上的点E、M、D入手,分别找出△OCE、△OAD、矩形OABC的面积之间的关系,列出等式求出k值。由矩形的中心对称性可设M(x,y),则B(2x,2y),解得xy=3,即k=3。
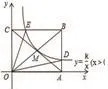
【点评】反比例函数与四边形的综合性题目是中考的重要考点,特别是反比例函数结合矩形、正方形的动点问题,更是最近几年的热门考点,活用设元法有时会让人感到豁然开朗,达到事半功倍的效果。
四、抽丝剥茧——智用点的坐标
例 5 已 知A(-4,n)、B(2, -4) 是 反 比 例 函 数
图象和一次函数y=kx+b的图象的两个交点。
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)直接写出关于x的不等式kx+b--的解。
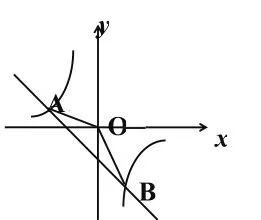
【分析】解决此类题目一般分三步走:(1)利用点的坐标求函数表达式;(2)求交点;(3)求面积。本题由B点坐标代入反比例函数表达式可求出m的值,从而确定反比例函数表达式,进而把A点代入已确定的反比例函数表达式,求出A点坐标,由A、B两点坐标确定一次函数解析式。求出一次函数与x轴或者y轴的交点坐标,把求△AOB的面积转化成求△AOC、△COB的面积和。
一次函数美,美在图象的刚劲、挺拔;反比例函数更美,美在反比例函数图象优雅、温柔的独特气质。反比例函数蕴含的知识是无穷尽的,值得我们时刻去探讨。反比例函数有关面积计算的题目亦是千变万化,解题方法多样,深刻理解反比例函数的性质是解题关键。
