几类高强度密码S盒的安全性新分析

赵 颖，叶 涛，韦永壮,3

(1.桂林电子科技大学 广西密码学与信息安全重点实验室，广西 桂林 541004;2.桂林电子科技大学 广西云计算与大数据协同创新中心，广西 桂林 541004;3.桂林电子科技大学 广西无线宽带通信与信号处理重点实验室, 广西 桂林 541004)(*通信作者电子邮箱walker_wyz@guet.edu.cn)

几类高强度密码S盒的安全性新分析

赵 颖1，叶 涛2，韦永壮1,3*

(1.桂林电子科技大学 广西密码学与信息安全重点实验室，广西 桂林 541004;2.桂林电子科技大学 广西云计算与大数据协同创新中心，广西 桂林 541004;3.桂林电子科技大学 广西无线宽带通信与信号处理重点实验室, 广西 桂林 541004)(*通信作者电子邮箱walker_wyz@guet.edu.cn)

针对几类高强度密码S盒是否存在新的安全性漏洞问题，提出了一种求解S盒非线性不变函数的算法。该算法主要基于密码S盒输入和输出的代数关系来设计。利用该算法对这几类密码S盒进行测试，发现其中几类存在相同的非线性不变函数;此外，如果将这些S盒使用于分组密码Midori-64的非线性部件上，将会得到一个新的变体算法。利用非线性不变攻击对其进行安全性分析，结果表明：该Midori-64变体算法存在严重的安全漏洞，即在非线性不变攻击下，存在264个弱密钥，并且攻击所需的数据、时间及存储复杂度可忽略不计，因此这几类高强度密码S盒存在新的安全缺陷。

S盒；非线性不变函数；Midori-64算法；非线性不变攻击；弱密钥

0 引言

对称密码算法由于具有加解密速度快、便于各种软件和硬件平台实现等优点，在网络与信息安全领域发挥着越来越重要的作用。对称密码的分析与设计是一对相互对立又相互统一的矛盾体，两者的互动推动着对称密码的发展[1]。密码S盒是对称密码算法的核心部件，其安全强度与算法的安全性息息相关[2]，比如经典的差分密码分析[3]、线性密码分析[4]、相关密码分析[5]、代数密码分析[6]等，都是基于密码S盒的统计特性来实现的。因此，设计及分析高强度的密码S盒是目前业界重要的研究热点。

在2011年美国国际密码年会上(Annual Cryptology Conference ,CRYPTO 2011)，Leander等[7]利用S盒混淆能力差的代数性质，提出一种新的分组密码攻击方法——不变子空间攻击，并对SP结构的分组密码算法PRINT进行不变子空间攻击，说明其存在严重的安全漏洞。进一步，在2015年的欧洲密码年会上(Annual International Conference on the Theory and Applications of Cryptographic Techniques, EUROCRYPT 2015)，Leander等[8]提出了不变子空间攻击的一般方法，并对三个密码算法Robin、iSCREAM和Zorro进行分析，发现iSCREAM存在一定的安全漏洞。在2016年亚洲密码年会上(International Conference on the Theory and Application of Cryptology and Information Security, ASIACRYPT 2016)，Todo等[9]利用密码S盒的输入和输出代数关系，提出了非线性不变攻击方法，并证明了不变子空间攻击是非线性不变攻击的一种特例。此外，针对轻量级分组密码算法Midori-64，他们还给出了一种非线性不变攻击方法。

在2017年国际快速软件加密会议上(International Conference on Fast Software Encryption, FSE 2017)，Guo等[10]提出了几类高强度的密码S盒，并说明这些新S盒足以抵抗不变子空间攻击。注意到，Guo等提出的几类新密码S盒是否足够安全？特别是当这些S盒部署在具体算法(比如Midori-64算法)的非线性组件里时，算法整体的安全性如何评价呢？这两个问题亟待解决。

本文利用密码S盒输入和输出的代数关系，设计了一个算法来寻找S盒的非线性不变函数。基于该算法，针对Guo等的几类S盒进行测试，结果表明：其中三类S盒存在相同的二次非线性不变函数。最后讨论了这三类S盒替换Midori-64算法的S盒后得到的Midori-64变体算法的安全性。

1 基础知识

1.1 五类高强度S盒

在FSE 2017上，Guo等[10]首先提出了两个概念：密码算法的密钥编排分类和S盒的设计目标。

密码算法的密钥编排分为以下两类：

1)密钥编排函数1(Key Schedule Function 1, KSF1)：每一轮都使用单密钥，如Midori-128、LED-64[11]；

2)密钥编排函数2(Key Schedule Function 2, KSF2)：两个密钥交替使用，如Midori-64、LED-128[11]。

S盒的设计目标按照其控制的弱密钥范围分为以下两类：

1)目标1(Goal 1)：确保弱密钥空间中含有的弱密钥的数目为c*2b，其中c为一个较小的常数，b为密钥含有的单元的个数；

2)目标2(Goal 2)：确保仅含有一个弱密钥。

Guo等[10]给出了五类新密码S盒的真值表，参见图1。其中x为S盒输入，y为S盒输出。其中S1，S2，S3是在KSF1和Goal 1的条件下，利用S盒的差分分布表，经过计算机搜索得到的；S4是在KSF2和Goal 1的条件下，利用S盒的差分分布表，经过计算机搜索得到的；S5是在KSF1和Goal 2的条件下，利用S盒的差分分布表，经过计算机搜索得到的。S1，S2，S3，S4，S5的最大差分可能性都为2-2，线性逼近的最大偏离值为2-2。

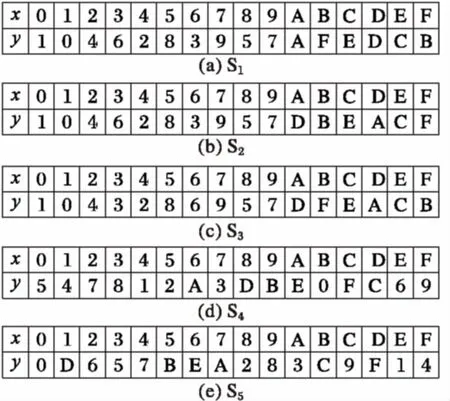
图1 五个新S盒的真值表

1.2 Midori-64算法

在ASIACRYPT 2015上，Banik等[12]提出Midori-64轻量级分组加密算法。Midori-64由于低功耗、低延时、轮数少等诸多优点得到了广泛关注。Midori-64的整体加密流程如图2所示。其中：P为输入的明文，C为输出的密文，WK为一个64比特的白化密钥，Ki(i=0,1,…,14)为第i轮加密时使用的子密钥，αi为64比特的轮常数，RKi(i=0,1,…,14)为异或轮常数αi之后的轮密钥。

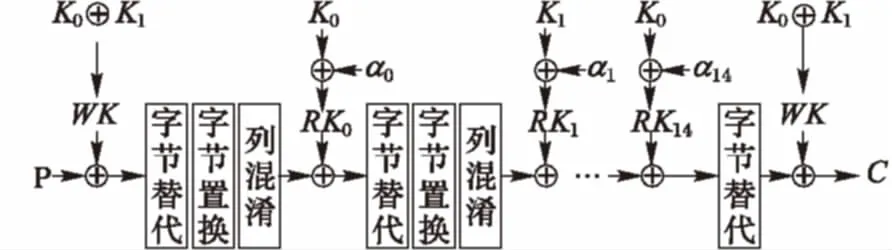
图2 Midori-64加密算法[12]

Midori-64密码算法每次可以处理64比特的数据，这64比特的数据被放在一个4×4的矩阵S中。

Midori-64算法的轮函数包括以下4个组件：字节替代、字节置换、列混淆、轮密钥加。下面分别介绍这4个组件。

1)字节替代(SubCell)。

使用一个非线性的4位S盒对每个单元的状态进行操作，Midori-64算法的S盒如图3所示。x为S盒输入，y为S盒输出。

图3 Midori-64算法的S盒

Fig. 3 S-box of Midori-64 algorithm

2)字节置换(ShuffleCell)。

字节置换主要是对矩阵S中的每一个位置按照如下顺序进行替换。

3)列混淆(MixColumn)。

Midori-64算法的列混淆矩阵为一个二进制的正交矩阵，列混淆矩阵如下：

4)轮密钥加(KeyAddition)。

轮密钥加将第i轮的密钥RKi与第i轮的状态异或。

Midori-64算法的密钥编排非常简单。128比特的密钥被表示成为两个64比特key0和key1，K=key0‖key1。WK=key0⊕key1,RKi=key(i mod 2)⊕αi，其中，αi每一个位置的最低位只有0或1两种情况，其他的位置为0，αi的部分编排如表1所示。

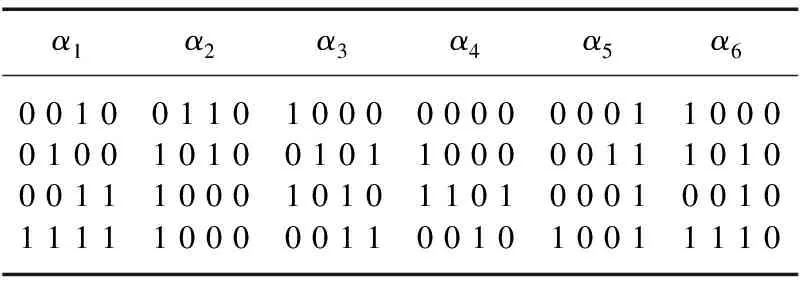
表1 Midori-64的部分轮常数[12]

2 不变子空间攻击和非线性不变攻击

2.1 不变子空间攻击和非线性不变攻击的基本思想

不变子空间和非线性不变攻击是两种弱密钥条件下的攻击方法。当且仅当输入每一轮加密轮函数的密钥都是弱密钥时，才能构造出概率为1的全轮区分器，进而利用这两种方法对算法进行攻击。注意到，近几年设计的若干轻量级密码算法为了提高加密的速度，减少消耗的内存，密钥编排算法简单。甚至直接将主密钥用于加密，这可能为攻击者所利用，从而进行非线性不变攻击和不变子空间攻击。

F(U+c)=U+d

(1)

则对应的弱密钥为k=u+c+d，其中u∈U，且有式(2)存在：

Fk(U+d)=F((U+d)+(u+c+d))=

F(U+c)=U+d

(2)

注意到，不变子空间攻击的本质思想是利用轮函数将空间U+c映射到U+d。如果输入的所有轮密钥为弱密钥，则上述性质(2)对于任意轮都是满足的。此外，U的维数决定了弱密钥空间的大小。假设U的维数为b，密钥一共含有m个单元，则对应的弱密钥空间为mb。

非线性不变攻击是不变子空间攻击的推广形式[9]，不变子空间攻击为非线性不变攻击的特例，在不变子空间中使用的非线性不变函数为指示函数δA(x)。

(3)

寻找轮函数的非线性不变函数g是非线性不变攻击的关键。非线性不变函数必须满足式(4)对于所有的输入xi-1都成立，其中，xi-1为轮函数的输入，xi为轮函数的输出，Constant为常数，此时输入的密钥定义为弱密钥。

g(xi-1)⊕g(xi)=Constant⊕g(keyi-1)

(4)

进一步，如果存在一个非线性不变函数可以穿透轮函数，并且每一轮输入的密钥都为弱密钥，那么此非线性不变函数同样也可以穿透这个轮函数相对应的密码算法，最终得到输入的明文和输出的密文之间满足g(P)+g(C)=Constant这样的关系，利用这种关系可以对SPN结构的分组密码算法进行弱密钥条件下的区分攻击。弱密钥空间为2m×(n-f)，其中n为S盒的位数，f代表非线性不变函数非线性部分所含的变量个数。

2.2 S盒非线性不变函数的求解方法

假设S盒的非线性不变函数存在，将S盒的非线性不变函数用代数正规型进行表示：

(5)

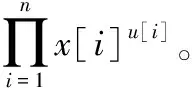
方法一 如果函数g为S盒的非线性不变函数，则对于所有的n比特的输入x和相应的n比特S盒的输出S(x)都满足式(6)：

g(x)+g(S(x))=Constant

(6)

转化为代数正规型的形式即为式(7)：

(7)

具体求解步骤如下：

步骤1 对于式(7)，固定λ1,λ2,…,λu的值(u的最大汉明重量取2)，固定常数Constant的值为0。

步骤2 遍历所有的x的值，如果对于所有的x和S(x)都有式(7)成立，则对应的Constant为0，保存此时的系数λ1，λ2,…,λu。

如果都有式(7)不成立，则对应的Constant为1，将此时的系数λ1,λ2,…,λu保存。

步骤3 改变λ1,λ2,…,λu的值，进行步骤2操作，直到遍历所有的λ1,λ2,…,λu。针对Constant取0和取1，分别得到若干组λ1,λ2,…,λu。

方法二 将式(7)进行变形得到如下的等式关系(8)：

(8)

对于式(8)，固定Constant为0，遍历所有的输入x，计算xu⊕S(x)u(u的最大汉明重量取2)，可以得到一个关于系数λ1，λ2，…，λu的方程组。如果方程组有解，则得到的解即为λ1,λ2,…,λu的值。固定Constant为1，利用上述Constant取0的同样方法求解λ1,λ2,…,λu。

3 五类高强度S盒的安全性新分析

本章设计了一个求解S盒非线性不变函数的算法，利用它对Guo等的几类S盒进行测试。进一步利用其中三类S盒存在非线性不变函数的缺陷，构造弱密钥条件下的区分器，进而对Midori-64变体进行非线性不变攻击。

3.1 S盒的非线性不变函数求解算法及其应用

本节设计了一个算法来求解4位S盒的非线性不变函数。具体步骤如下：

步骤1 针对S盒遍历所有的输入x，得到对应的输出为y，并将对应的x、y按行分别存储在矩阵X、Y中。

步骤2 建立两个16×10的矩阵X1、Y1，其中，X1[0][0]～X1[0][3]中存储x[0][0]～x[0][3]的值，X1[0][4]～X1[0][9]中存储x[0][i]*x[0][j] 的值，i，j为 [1，2，3，4]中两个不重复的数。Y1[0][0]～Y1[0][3]中存储的为y[0][0]～y[0][3]的值，Y1[0][4]～Y1[0][9]中存储y[0][i]*y[0][j]的值，i，j为 [1，2，3，4]中两个不重复的数。同理，按照以上的方法对X1、Y1、X、Y第1～15行执行同样的操作。最终输出矩阵X1，Y1。

步骤3X1，Y1中每一个位置的值按位异或，得到一个新的矩阵Z。

步骤4 定义一个10维的向量A，向量中的每一个位置的值只有0或1两种情况，遍历A中的所有的值，对于每一种情况，用Z*A，最终得到一个列向量。如果列向量中的值都相等，则保存A中的对应的值到A1中。

步骤5A1中的每一行代表一个非线性不变函数的表达式。第1～3列代表的系数为λ1～λ3，第4～9列代表的系数为λ12,λ13,λ14,λ23,λ24,λ34。每一行数值为1时表示系数存在，数值为0时表示系数不存在。至此恢复二次非线性不变函数的一次和二次项系数，也就得到了此S盒的二次非线性不变函数。

利用此算法对Guo等提出的几类S盒进行测试，结果表明：S1、S2、S3存在相同的二次非线性不变函数，参见式(9)。S4、S5不存在二次非线性不变函数。

g(x)=x[2]⊕x[3]⊕x[4]⊕x[2]·x[3]

(9)

3.2 Midori-64变体的非线性不变攻击

分别用含有非线性不变函数的三类S盒即S1、S2、S3部署在Midori-64的S盒组件上，结果表明：Midori-64变体算法存在严重的安全漏洞，即弱密钥空间为264。

具体分析过程如下：

对于S盒，利用寻找到的非线性不变函数g，可以得到式(10)对于所有的S盒都成立：

g(xi)⊕g(S(xi))=0

(10)

其中:xi为一个第i个S盒的输入，S(xi)为第i个S盒输入为xi时对应的输出。又知Midori-64的S层一共采用了16个相同的S盒，可以得到关于S层的非线性不变函数，参见式(11):

(11)

经过S层后，算法将通过字节置换，由于字节置换作用于每一个位置。所以，式(11)经过字节置换后仍旧成立。又知Midori-64的列混淆矩阵为正交矩阵，yi为第i个位置经过L层后的输出。利用Todo等[9]的结论：如果针对S层的非线性不变函数的最高阶数为二次，并且列混淆矩阵是正交矩阵，则S层的非线性不变函数对于L层同样也是成立的。可得式(12)是恒成立的：

(12)

最后进行轮密钥加，轮密钥RKi的编排为RKi=Ki mod 2⊕αi，αi为轮常数。Midori-64的轮常数每一个位置的十六进制形式仅包含0或1，转化为4位的二进制后，在第2、3位都为零。为了保证密钥RKi对于非线性不变函数为线性的运算，需要K0，K1每个单元的第2、3位固定为0，其他的位置可以为任意的值。此时的密钥为弱密钥，弱密钥空间为264。如果输入的密钥满足以上条件，则轮函数经过轮密钥加后存在式(13)成立：

(13)

Midori-64一共加密了16轮，如果每一轮输入的密钥都为弱密钥，则根据式(13)可以得到输入的明文和密文之间的关系如式(14)、(15)：

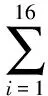
(14)

(15)

当输入的密钥不是弱密钥时，式(15)成立的概率为0.5。当输入的密钥为弱密钥时，式(15)以概率1成立。所以，判断输入的密钥是否为弱密钥时，需要输入明文和密文对进行验证，输入N对明密文，如果均满足式(15)，则使用的密钥不是弱密钥的概率为2-N+1；如果至少存在一对明密文不满足，则使用的密钥不是弱密钥。当明密文对的数目取40时，可知弱密钥条件下，可以以概率1-2-40+1=1构造出区分器。随后利用此区分器对密码算法进行区分攻击。在Midori-64的密码分组链接(Cipher Block Chaining, CBC)工作模式下，输入相同的明文和不同的初始向量IV，得到不同的密文。根据非线性不变函数式(6)得到式(16)：

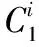
(16)

此公式包含32个未知数，需要输入33个不同的IV得到32个不同的表达式。利用高斯消元方法求解此32个表达式组成的方程所需的时间复杂度为323次简单运算。存储复杂度为N个分组长度，数据复杂度为N。

综上，利用Guo等提出的S盒替换Midori-64的S盒后， Midori-64变体算法的弱密钥为264个。注意到，Guo等设计的S1、S2、S3是应用在KSF1模式下，达到的目标为：存在的弱密钥为c*2b个。Midori-64的密钥编排模式遵循KSF2，此时Midori-64变体的弱密钥空间远远大于c*2b。因此 Guo等设计的S1，S2，S3三类S盒没有达到最初的设计目标，无法抵抗非线性不变攻击。

4 结语

本文主要对Guo等设计的几类S盒的安全性进行了新的评估。给出了求解S盒非线性不变函数的新算法，利用新算法测试Guo等的五类S盒。结果表明：其中S1、S2、S3存在相同的二次非线性不变函数。此外，用这三类S盒直接替换Midori-64的S盒来得到Midori-64变体算法，结果表明：Midori-64变体算法存在严重的安全漏洞。因此，这三类S盒是不安全的。

References)

[1] LAI X. On the design and security of block ciphers [EB/OL]. [2016- 12- 16]. https://www.researchgate.net/publication/242506184_On_the_design_and_security_of_block_ciphers.

[2] 草冠杰,马建设,程雪岷.基于组合式爬山算法提高S盒非线性度的方法[J].计算机应用, 2015,35(8):2195-2198.(CAO G J, MA J S, CHENG X M. Method for increasing S-box nonlinearity based on combination of hill climbing [J]. Journal of Computer Applications, 2015, 35(8): 2195-2198.)[3] BIHAM E, SHAMIR A. Differential cryptanalysis of the full 16-round DES [C]// Annual International Cryptology Conference, LNCS 740. Berlin: Springer, 1992: 487-496.

[4] MATSUI M. Linear cryptanalysis method for DES cipher [C]// Workshop on the Theory and Application of of Cryptographic Techniques, LNCS 765. Berlin: Springer, 1993: 386-397.

[5] BIHAM E. New types of cryptanalytic attacks using related keys [J]. Journal of Cryptology, 1994, 7(4): 229-246.

[6] COURTOIS N T, PIEPRZYK J. Cryptanalysis of block ciphers with overdefined systems of equations [C]// International Conference on the Theory and Application of Cryptology and Information Security, LNCS 2501. Berlin: Springer, 2002: 267-287.

[7] LEANDER G, ABDELRAHEEM M A, ALKHZAIMI H, et al. A cryptanalysis of PRINTcipher: the invariant subspace attack [C]// Annual Cryptology Conference, LNCS 6841. Berlin: Springer, 2011: 206-221.

[8] LEANDER G, MINAUD B, RØNJOM S. A generic approach to invariant subspace attacks: cryptanalysis of Robin, iSCREAM and Zorro [C]// Annual International Conference on the Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2015: 254-283.

[9] TODO Y, LEANDER G, SASAKI Y. Nonlinear invariant attack: practical attack on full SCREAM, iSCREAM, and Midori64 [EB/OL]. [2016- 11- 06]. http://eprint.iacr.org/2016/732.pdf.

[10] GUO J, JEAN J, NIKOLIC I, et al. Invariant subspace attack against Midori64 and the resistance criteria for S-box designs [J]. IACR Transactions on Symmetric Cryptology, 2016, 2016(1): 33-56.

[11] GUO J, PEYRIN T, POSCHMANN A, et al. The LED block cipher [C] // International Workshop on Cryptographic Hardware and Embedded Systems, LNCS 6917. Berlin: Springer, 2011: 326-341.

[12] BANIK S, BOGDANOV A, ISOBE T, et al. Midori: a block cipher for low energy [C]// International Conference on the Theory and Application of Cryptology and Information Security, LNCS 9453. Berlin: Springer, 2014: 411-436.

Newsecurityanalysisofseveralkindsofhigh-levelcryptographicalS-boxes

ZHAO Ying1, YE Tao2, WEI Yongzhuang1,3*

(1.GuangxiKeyLaboratoryofCryptographyandInformationSecurity,GuilinUniversityofElectronicTechnology,GuilinGuangxi541004,China;2.GuangxiCooperativeInnovationCenterofcloudcomputingandBigData,GuilinUniversityofElectronicTechnology,GuilinGuangxi541004,China;3.GuangxiKeyLaboratoryofWirelessWidebandCommunicationandSignalProcessing,GuilinUniversityofElectronicTechnology,GuilinGuangxi541004,China)

Focusing on the problem whether there are new security flaws of several kinds of high-level cryptographic S-boxes, an algorithm for solving the nonlinear invariant function of S-boxes was proposed, which is mainly based on the algebraic relationship between the input and output of the cryptographic S-boxes. Using the proposed algorithm, several kinds of S-boxes were tested and it was found that several of them had the same nonlinear invariant function. In addition, if these S-boxes were used to non-linear parts of the block cipher Midori-64, a new variant algorithm would be obtained. The security analysis was carried out by non-linear invariant attack. The analytical results show that the Midori-64 variant is faced with serious secure vulnerability. In other words, there exist 264weak keys when nonlinear invariant attack is applied to the Midori-64 variant, meanwhile data, time and storage complexity can be neglected, consequently some high-level cryptographic S-boxes have security flaws.

S-box; nonlinear invariant function; Midori-64 algorithm; nonlinear invariant attack; weak key

2017- 03- 17;

2017- 04- 29。

国家自然科学基金资助项目(61572148)；广西自然科学基金(杰出青年基金)资助项目(2015GXNSFGA139007)；广西高等学校优秀中青年骨干教师培养工程项目(第2期)。

赵颖(1991—)，女，陕西咸阳人，硕士研究生，主要研究方向：分组密码的分析与设计； 叶涛(1991—)，男，黑龙江伊春人，硕士研究生，主要研究方向：分组密码的设计与分析； 韦永壮(1976—)，男，广西田阳人，教授，博士，主要研究方向：密码学。

1001- 9081(2017)09- 2572- 04

10.11772/j.issn.1001- 9081.2017.09.2572

TP309.7

A

This work is partially supported by the National Natural Science Foundation of China (61572148), the Guangxi Natural Science Fund (Fund for Distinguished Young Scholars) (2015GXNSFGA139007), the Project of Outstanding Young Teachers Training in Higher Education Institutions of Guangxi (the second period).

ZHAOYing, born in 1991, M. S. candidate. Her research interests include analysis and design of block cipher .

YETao, born in 1991, M. S. candidate. His research interests include analysis and design of block cipher.

WEIYongzhuang, born in 1976, Ph. D. ,professor. His research interest include cryptography.