基于模糊高斯学习策略的粒子群-进化融合算法

周 伟，罗建军，靳 锴，王 凯

(1.西北工业大学 航天学院，西安 710072； 2.火箭军工程大学 理学院，西安 710025)(*通信作者电子邮箱zw_yj@163.com)

基于模糊高斯学习策略的粒子群-进化融合算法

周 伟1*，罗建军1，靳 锴1，王 凯2

(1.西北工业大学 航天学院，西安 710072； 2.火箭军工程大学 理学院，西安 710025)(*通信作者电子邮箱zw_yj@163.com)

针对粒子群优化(PSO)算法存在的开发能力不足，导致算法精度不高、收敛速度慢以及微分进化算法具有的探索能力偏弱，易陷入局部极值的问题，提出一种基于模糊高斯学习策略的粒子群-进化融合算法。在标准粒子群算法的基础上，选取精英粒子种群，运用变异、交叉、选择进化算子，构建精英粒子群-进化融合优化机制，提高粒子种群多样性与收敛性；引入符合人类思维特性的模糊高斯学习策略，提高粒子寻优能力，形成基于模糊高斯学习策略的精英粒子群和微分进化融合算法。对9个标准测试函数进行了计算测试和对比分析，结果表明函数Schwefel.1.2、Sphere、Ackley、Griewank与Quadric Noise计算平均值分别为1.5E-39、8.5E-82、9.2E-13、5.2E-17、1.2E-18，接近算法最小值；Rosenbrock、Rastrigin、Schwefel及Salomon函数收敛平均值较四种对比粒子群优化算法计算结果提高了1～3个数量级；同时，收敛性显示算法收敛速度较对比算法提高了5%～30%。算法在提高计算收敛速度和精度上效果明显，具有较强的逃离局部极值的能力和全局搜索能力。

模糊隶属度；高斯学习；粒子群；微分进化；融合优化

0 引言

粒子群优化(Particle Swarm Optimization, PSO)算法是一种群体智能优化计算技术，起源于对简单社会系统的模拟，如鸟群和鱼群觅食过程中生物体相互协作行为启发，由Kennedy等[1]于1995年首次提出。算法基于迭代随机搜索优化机制，具有概念简单、便于实现、参数较少和无需梯度信息等优点，一经提出就得到了众多学者的普遍关注，目前在图像处理、信息挖掘、模式识别、路径优化以及人工智能等领域得到广泛应用[2-4]。

标准粒子群优化(Standard Particle Swarm Optimization, SD-PSO)算法作为一种新型群智能优化算法相比其他优化算法具有许多突出的优点，但算法在处理多极值复杂问题时，仍然存在开发能力弱的缺点，导致收敛速度慢、算法精度低等问题。针对SD-PSO算法存在的缺陷，学者们提出了许多改进的优化策略[5-6]。Shi等[7]研究提出了采用模糊系统动态改变惯性权重的策略提高算法开发能力，并以Rosenbrock函数验证了改进算法的有效性；Clerc等[8]提出采用收缩因子提高收敛速度，增强算法稳定性和收敛速度；Nickabadi等[9]引入粒子适应度，提出自适应粒子群(Adaptive Particle Swarm Optimization, AD-PSO)算法，自适应地调整惯性权重来加强从局部最优中逃脱的能力，以提高达到大规模问题的全局最小值的能力。Kao等[10]将遗传算法与PSO算法相结合，提出遗传-粒子群优化算法，强化了对粒子间区域的搜索能力以及逃离局部极值的能力；Guo等[11]将文化算法引入PSO形成CA-PSO(Culture and Particle Swarm Optimization)算法，通过信仰与群体两层空间的演化与交流，完成粒子群体优化。周新宇等[12]、赵嘉等[13]将反向学习策略引入群优化算法，提出多种精英反向学习粒子群优化算法，通过在标准测试函数上的对比认为动态随机反向学习精英粒子群优化(Dynamic Random Opposition-based learning Elite Particle Swarm Optimization, DR-EOPSO)算法性能最优。

尽管改进算法优化性能有所提高，但到目前为止依然很难在提高算法收敛速度和逃离局部最优两个方面达到平衡，例如CA-PSO算法每次迭代需经过两层串行演化，为此增加了计算量，降低了收敛速度。而GA-PSO算法引入交叉算子后虽然提高了粒子交叉多样性，但由于交叉算子形式简单，使得空间搜索能力提高有限，却增加了算法的复杂度。

Chakrabory等[14]认为微分进化算法具有开发能力强、探索能力弱的特点。因此，本文在精英粒子群算法的基础上，引入变异、交叉、选择进化算子，构建精英粒子群-进化融合优化机制，保持粒子种群多样性，提高粒子全局最优的探索与开发能力。此外，为进一步提高粒子学习搜索能力，引入符合人类思维特性的高斯学习策略，形成基于高斯学习策略的精英粒子群进化算法(Elite Particle Swarm Optimization and Evolutionary algorithm based on Gaussian learning strategy, GE-PSO)。对9个标准测试函数[15-17]开展了仿真计算，计算结果表明，本算法在提高计算收敛速度和精度上效果明显，特别在处理多峰值函数优化方面，增强了粒子逃离局部极值的能力和全局搜索能力，与文中所选对照算法相比，具有显著优势。

1 标准粒子群算法

假设粒子群体规模为n，目标搜索空间的维度为d，其中每个粒子都有位置x和速度v两个属性，第i个粒子当前的速度表示为v=(vi1,vi2,…,vid)，位置则表示为x=(xi1,xi2,…,xid)。优化过程中，每一次迭代都根据两个最优值来更新自己，一个是粒子i个体历史最优值pbesti，表示为pbesti=(pi1,pi2,…,pid)，另一个是群体历史最优值gbest。粒子速度和位置迭代更新公式如下：

(1)

其中：i=1,2,…,n，j=1,2,…,d，w为惯性权重，c1和c2为正的学习因子，r1和r2为0～1均匀分布的随机数。

2 高斯学习策略

从SD-PSO算法看出，学习因子c1、c2对粒子收敛速度具有十分重要的影响，学习因子使粒子具有自我总结和向群体中优秀个体学习的能力，从而向群体内或邻域内的最优点靠近。c1、c2分别调节微粒向个体最优和群体最优方向飞行的最大步长，决定微粒个体经验和群体经验对微粒自身运行轨迹的影响，反映微粒群体之间的信息交流。通常c1调节粒子飞向自身最好位置方向的步长，c2则调节粒子飞向全局最好位置方向的步长，当学习因子较小时，可能使微粒远离目标区域内徘徊，而学习因子较大时，可使微粒迅速向目标区域移动，甚至越过目标区域。因此c1、c2的不同取值，将影响到PSO算法的性能。

传统的SD-PSO算法认为寻优过程所有粒子的各学习因子始终都为相同正常数，也就是说所有粒子社会学习与自我学习的能力都是相同的，这会使粒子搜索能力逐渐趋同，从而加速局部早熟，在应对复杂多峰值问题优化时往往导致初期收敛步长较小，后期收敛步长又过大，严重影响收敛速度和精度。

受人类智能和社会行为的启发，认为每个粒子如同每个人一样，其学习能力是不同的，且每一粒子在不同维度方向上的学习能力也是有差别的[5]，这样可以避免粒子开发能力趋同，也可以提高粒子多样性。同时引入符合人类思维特性的模糊高斯函数学习策略，将模糊隶属度函数表示为随学习因子cij,1变化的高斯函数式(2)，如图1所示。

(2)

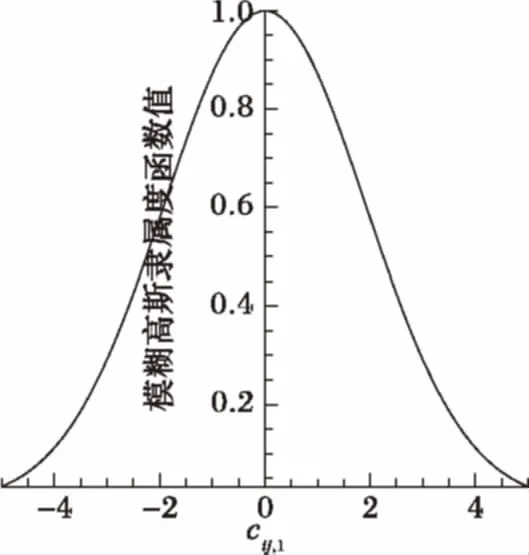
图1 模糊高斯隶属度函数

其中，G()为高斯隶属度函数，i=1,2,…,n；r为[0,1]区间随机扰动，反映粒子的不同学习效率；δ为高斯隶属函数参数。由于目标函数值模糊变量小，因此隶属度函数一般可采用线性函数表达，使隶属度直接与函数值排列顺序成正比，形式如式(3)：

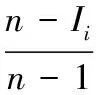
(3)

其中：n为粒子种群数；Ii是排列后第i个目标值的序列号；Gmax为最大隶属度，通常为1；Gmin为最小隶属度，本文取0.011 1(3σ准则)。由模糊推理条件扩展到问题的第j维度得到隶属度函数：

Gij=rand(Gi,1)

(4)

参数δi可由式(5)确定：

δi=b|ximin-xrand|

(5)

b=(itermax-iter)/itermax

(6)

其中：iter为迭代次数；itermax为最大迭代次数；b是迭代系数；ximin为群体内第i个粒子的最佳位置；xrand为当前群体内随机产生的粒子位置。

综上可得粒子学习因子cij,1的计算公式如下：

(7)

粒子社会学习因子cij,2可按式(8)方法选取：

cij,2=|1-cij,1|

(8)

式(8)说明，对于每一个粒子当其自学能力较弱的时候，提高其社会学习能力，将有助于提高其全局搜索能力，反之当粒子自学能力较强时，适当降低其社会学习能力有助于提高个体收敛速度。

3 精英粒子群进化算法

3.1 算法原理

在SD-PSO算法中，粒子仅向群体历史最优值gbest和自身历史最优值Pbesti学习。而对比人类社会，人类不仅向最好的个体学习，还向身边较好的个体学习，向社会精英阶层学习。精英粒子群体既保留了优秀粒子信息，更有与普通粒子一致的数据环境和约束条件，既不激进也不落后，代表了粒子群整体信息熵的发展趋势和方向。因此，提高了粒子群掉入局部最优的免疫能力，种群的搜索范围扩大，粒子会飞向更多新的位置，粒子更容易发现最优值；通过粒子间的相互学习，粒子会向更优的位置移动，有可能会跳出局部最优解，具有比SD-PSO算法更好的收敛性与鲁棒性。

受此启发，在基于高斯学习策略PSO算法的每一代中选取适应度函数排序前10%作为精英粒子群E，并在精英粒子群中随机选取一个精英粒子作为学习的模板。在原有粒子迭代更新的基础上，增加精英粒子学习项。迭代公式如下：

(9)

其中：i=1,2,…,n，j=1,2,…,d，g为粒子进化代数，ebesti=(ei1,ei2,…,eij)为随机选择的精英粒子的位置，cij,1为个体学习因子，按式(7)计算；cij,2为社会学习因子按式(8)计算；cij,3为精英学习因子，按式(10)计算。

cij,3=(cij,1+cij,2)/2;i=1,2,…,n,j=1,2,…,d

(10)

w为惯性权重，本文采用线性递减惯性权重:

(11)

在精英粒子群优化算法的基础上，为提高种群多样性，引入进化变异算子：

(12)

其中：Uij为粒子i在j维上的变异值，F为随机数。

采用交叉操作(式(13))确定突变粒子是否作为备选粒子，交叉概率因子CRi(g)取随机数；

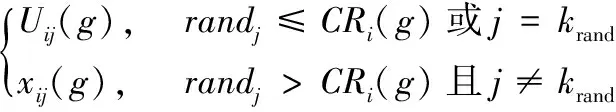
(13)

对比指标函数适应值，选择最优粒子如式(14)，形成新一代个体：

(14)

3.2 算法步骤

算法的具体步骤如下：

步骤1 随机生成初始种群粒子，并确定计算参数，如惯性权重ω、迭代系数b、精英粒子群数N等；

步骤2 计算和评价每个粒子的适应值Q|(xij)；

步骤3 根据适应度函数值排序，并确定精英粒子群E；

步骤4 按照式(7)、(8)、(10)分别计算高斯学习因子cij,1、cij,2、cij,3，代入式(9)更新粒子速度、位置；

步骤5 选择基准粒子，并根据式(12)进行变异操作，生成突变体；

步骤6 按照式(13)，采用交叉操作确定突变体是否作为备选体；

步骤7 选择操作，根据式(14)通过指标函数比较选取合适的新一代个体；

步骤8 重复步骤2～7过程迭代，直到指标函数满足要求或达到最大迭代次数。

4 仿真及分析

4.1 测试函数

为了测试本文提出的基于高斯学习策略的粒子群遗传进化算法，选择了9个经典的Benchmark测试函数进行测试仿真，如表1所示。其中f1～f4为单峰函数，在搜索范围内只有一个极值点，主要检验算法的收敛速度和寻优精度；f5～f9为多峰函数，在搜索范围内有多个局部极值点，主要考察算法的全局搜索能力和逃离局部最优的能力。测试函数及测试算法在Matlab 2013b(64 b)数值计算软件中实现，运行环境为Windows 7双核，4 GB内存，3.0 GHz CPU。

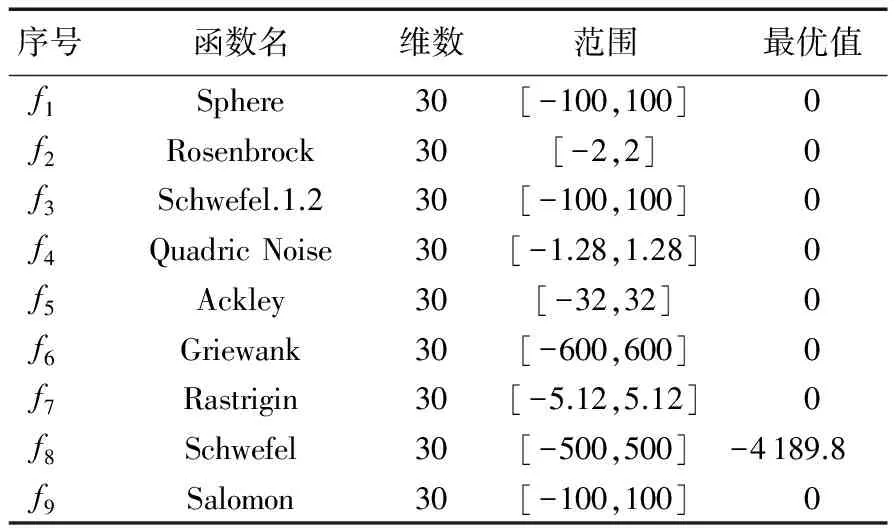
表1 Benchmark测试函数

4.2 仿真实验算法

为了更好地对比测试本文算法的性能，将本文的算法与当前较流行的标准PSO算法、文化PSO算法、自适应PSO算法和动态随机反向学习精英PSO算法的测试结果进行比较，算法的英文简称分别为：GE-PSO、SD-PSO、CA-PSO、AD-PSO和DR-EOPSO。各算法的参数设置见表2。

为了在相同条件下进行比较，所有算法的种群规模Psize=30，测试维数Dim=30，迭代次数Num=5 000，同时为消除随机性对算法的影响，每种算法对每个测试函数独立运行30次，取平均值和标准差作为测试结果。

表2 算法的参数设置

4.3 结果及分析

4.3.1 仿真结果

采用5种算法对f1～f9测试函数分别进行了仿真计算，各函数计算所得均值及标准差如表3所示。图2、3为各函数优化过程收敛曲线，由于各函数适应度不同，且数值差异较大，为清晰地显示实验结果，更加客观准确地对比算法优劣，收敛过程对适应度函数值均采用了以10为底的对数(lg)。

由表3中各函数适应度平均值计算数据可以分析得出，除f3、f4两单峰函数外，本文算法的计算结果均优于其余测试粒子群算法结果，特别是多峰值函数的寻优效果更为突出。从各不同算法的计算数据对比来看，CA-PSO算法计算结果与本文提出的GE-PSO算法计算结果较为接近。标准PSO算法表现最差，且极易陷入局部极小值而终止进化；AD-PSO算法较标准PSO有了明显改进，但结果较其余三种算法还有较大的差距。

图2 单峰函数计算收敛曲线

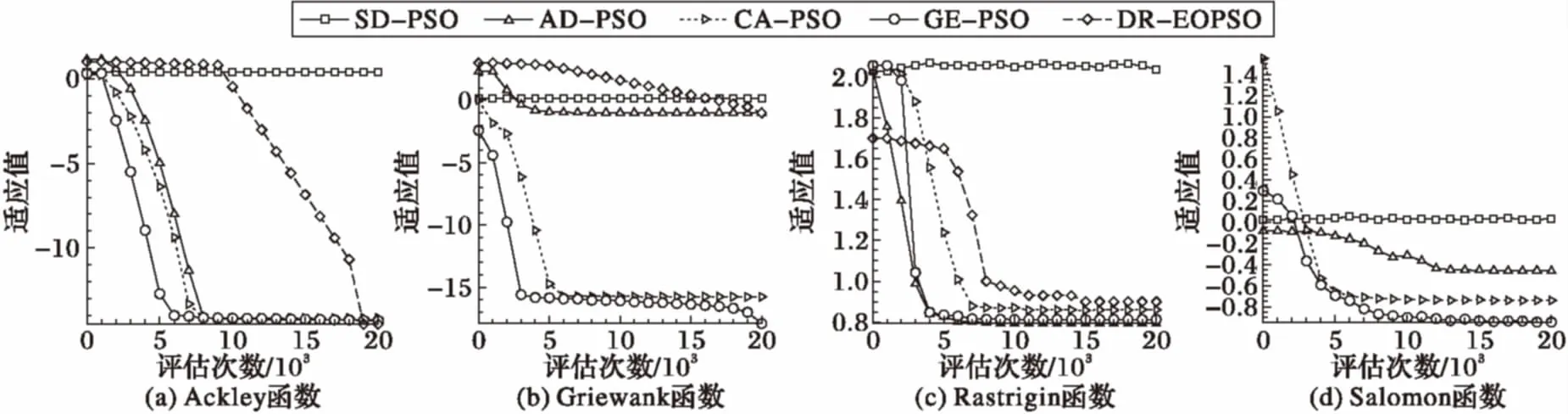
图3 多峰函数计算收敛曲线

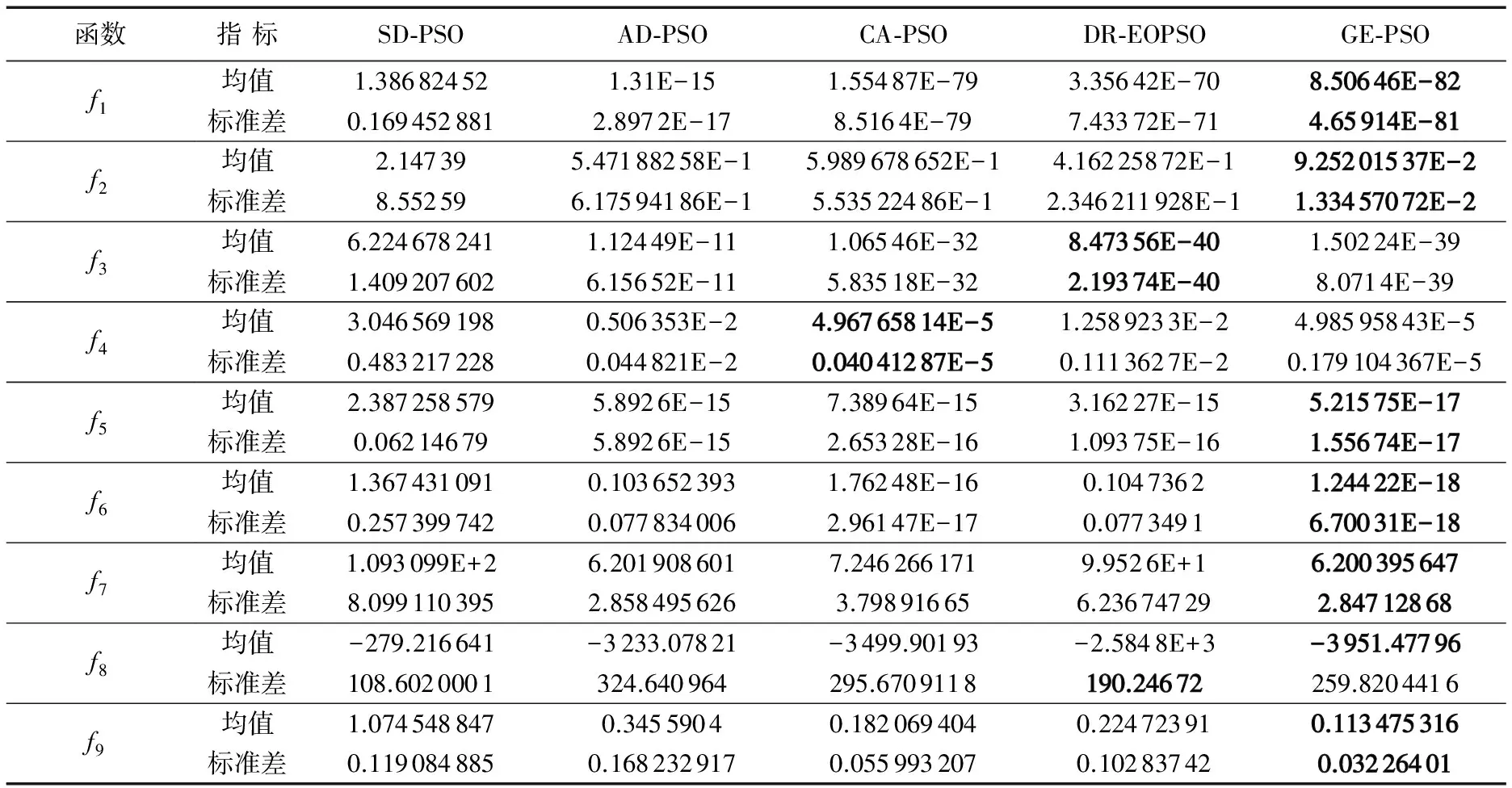
表3 仿真测试结果

从算法稳定性的角度分析表中各函数计算标准差，除f3、f4及f8外，本文提出的GE-PSO算法的稳定性优于其他算法。标准PSO算法稳定性最差，其余3种算法的稳定性介于标准PSO算法与GE-PSO算法之间。

4.3.2 收敛性分析

为了更加清晰地表征不同算法在进化过程中的收敛速度与性能，本文给出了5种算法在9个测试函数10维上的寻优进化历程图，如图2、3所示。其中，横轴为评估次数，纵轴为适应度函数值的对数值。通过对比曲线图1中的4个单峰函数曲线可知，GE-PSO算法相比其他4种算法，除了f3的收敛效果不明显外，其余3个函数不论收敛速度还是收敛精度都好于其他4种算法，且各函数在1万次迭代左右就已找到或接近最优值0。从曲线图2可以看出，GE-PSO算法在处理多峰值函数优化问题上也具有很好的优势，收敛速度明显较其他5种算法更快，且寻找的函数最优值收敛精度也是最高的。结合图2和图3可知，本文提出的GE-PSO算法无论在处理单峰值函数还是多峰值函数寻优问题上，都具有较好的优势，算法收敛速度快，寻优精度高，收敛一致性好，未出现收敛速度时快时慢不一致的问题。

4.3.3 统计T检验

为进一步从统计意义上进行分析比较，本文对计算数据引入统计t检验测试实验，以此分析并判断本文提出的算法与其他4种算法在性能上是否存在显著性差异。由于算法数据存在方差非齐次性，因此本文采用方差非齐次t检验实验方法进行测试，t检验的分位数为单侧0.05，自由度为30，t检验的临界值通过查表得为1.697。即当检验t值>1.697时，说明本文算法显著优于其他算法，标记为“+”；当检验t值<-1.697时，说明本文算法显著差于其他算法，标记为“-”；否则，说明本文算法与其他算法无显著差异，标记为“=”。在statistics一栏中按照U(优于个数)/E(等于个数)/L(小于个数)的方式以本文算法为参照进行统计，结果见表4所示。

表4 算法显著性差异检验结果

5 结语

针对粒子群算法进化速度慢、易陷入局部极值和算法精度低等问题，提出一种基于高斯学习策略的精英粒子群-微分进化融合算法(GE-PSO)。在SD-PSO算法的基础上，引入高斯学习策略，提高粒子学习搜索能力；以一定比例(10%)确定当代精英群体，以提高算法的开发能力，提高算法精度；融合变异、交叉、选择进化操作提高粒子种群多样性以增加逃离局部最优的能力。为检验算法性能，对比4种PSO算法，对9个标准测试函数进行了数值仿真实验。经计算精度、收敛性与统计t检验分析表明，本文算法在提高计算收敛速度和精度上优于其他四种粒子群优化算法，特别在处理多峰值函数优化方面效果明显，增强了粒子逃离局部极值的能力和全局搜索能力，具有显著优势。下一步应在降低算法计算复杂度、并行计算以及扩大算法应用领域等问题上作进一步深入研究。

References)

[1] KENNEDY J, EBERHART R C. Particle swam optimization [C]// Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway, NJ: IEEE, 1995: 1942-1948.

[2] SYULISTYO A R, PURNOMO D M J, RACHMADI M F, et al. Particle Swarm Optimization (PSO) for training optimization on Convolution Neural Network (CNN) [J]. Jurnal Ilmu Komputer dan Informasi (Journal of Computer Science and Information), 2016, 9(1): 52-58.

[3] PATEL H. Accelerated PSO swarm search feature selection with SVM for data stream mining big data [J] . International Journal of Research and Engineering, 2016, 3(9): 15761-15765.

[4] MARINI F, WALCZAK B. Particle Swarm Optimization (PSO). A tutorial [J]. Chemometrics and Intelligent Laboratory Systems, 2015, 149(12): 153-165.

[5] 李俊,汪冲,李波,等.基于多策略协同作用的粒子群优化算法[J].计算机应用,2016,36(3): 681-686.(LI J, WANG C, LI B, et al. Particle swarm optimization algorithm based on multi-strategy synergy [J]. Journal of Computer Applications, 2016, 36(3): 681-686.)

[6] 王曙燕，温春琰，孙家泽.基于自适应粒子群优化算法的测试数据扩增方法[J].计算机应用,2016,36(9):2492-2496.(WANG S Y, WEN C Y, SUN J Z. Test data augmentation method based on adaptive particle swarm optimization algorithm [J]. Journal of Computer Applications, 2016, 36(9): 2492-2496.)

[7] SHI Y, MEMBER S, EBERHART R, et al. Implementation of evolutionary fuzzy systems [J]. IEEE Transactions on Fuzzy System, 1999, 7(2): 109-119.

[8] CLERC M, KENNEDY J. The particle swarm—explosion, stability, and convergence in a multidimensional complex space [J]. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73.

[9] NICKABADI A, EBADZADEH M M, SAFABAKHSH R. A novel particle swarm optimization algorithm with adaptive inertia weight [J]. Applied Soft Computing, 2011, 11(4): 3658-3670.

[10] KAO Y T, ZAHARA E. A hybrid genetic algorithm and particle swarm optimization for multimodal functions [J]. Applied Soft Computing, 2008, 8(2): 849-857.

[11] GUO Y N, YANG Z, WANG C, et al. Cultural particle swarm optimization algorithms for uncertain multi-objective problems with interval parameters [M]// Natural Computing. Berlin: Springer, 2016: 1-22.

[12] 周新宇，吴志健，王晖，等.一种精英反向学习的粒子群优化算法[J].电子学报,2013,41(8):1647-1652.(ZHOU X Y, WU Z J, WANG H, et al. Elite opposition-based particle swarm optimization [J]. Acta Electronica Sinica, 2013, 41(8): 1647-1652.)

[13] 赵嘉，付平，李崇侠，等.基于不同学习模型的精英反向粒子群优化算法[J].小型微型计算机系统,2015,36(6):1368-1372.(ZHAO J, FU P, LI C X, et al. Particle swarm optimization based on elite opposition learning using different learning models [J]. Journal of Chinese Computer Systems, 2015, 36(6): 1368-1372.)

[14] CHAKRABORTY U K, DAS S, KONAR A. Differential evolution with local neighborhood [C]// Proceedings of the 2006 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2006: 2042-2049.

[15] TANG K, LI X D, SUGANTHAN P N, et al. Benchmark functions for the CEC ’2010 special session and competition on large-scale global optimization [EB/OL]. [2016- 11- 14]. http://www.al-roomi.org/multimedia/CEC_Database/CEC2010/LargeScaleGlobalOptimization/CEC2010_LargeScaleGO_TechnicalReport.pdf.

[16] 刘建华.粒子群算法的基本理论及其改进研究[D].长沙:中南大学社,2009:223-275.(LIU J H. The basic theory of particle swarm optimization and its improvement [D]. Changsha: Central South University, 2009: 223-275.)

[17] 王维博.粒子群优化算法研究及其应用[D].成都：西南交通大学,2012.(WANG W B. Research on particle swarm optimization algorithm and its application [D]. Chengdu: Southwest Jiaotong University, 2012.)

ParticleswarmanddifferentialevolutionfusionalgorithmbasedonfuzzyGausslearningstrategy

ZHOU Wei1*, LUO Jianjun1, JIN Kai1, WANG Kai2

(1.CollegeofAstronautics,NorthwesternPolytechnicalUniversity,Xi’anShaanxi710072,China;2.CollegeofScience,RocketForceUniversityofEngineering,Xi’anShaanxi710025,China)

Due to the weak development ability, Particle Swarm Optimization (PSO) algorithms have the shortages of low precision and slow convergence. Comparatively weak exploration ability of Differential Evolution (DE) algorithm, might further lead to a trap in the local extremum. A particle swarm-differential evolution fusion algorithm based on fuzzy Gaussian learning strategy was proposed. On the basis of the standard particle swarm algorithm, the elite particle population was selected, and the fusion mechanism of elite particle swarm-evolution was constructed by using mutation, crossover and selection evolution operators to improve particle diversity and convergence. A fuzzy Gaussian learning strategy according with human thinking characteristics was introduced to improve particle optimization ability, and further generate an elite particle swarm and differential evolution fusion algorithm based on fuzzy Gaussian learning strategy. Nine benchmark functions were calculated and analyzed in this thesis. The results show that the mean values of the functions Schwefel.1.2, Sphere, Ackley, Griewank and Quadric Noise are respectively 1.5E-39, 8.5E-82, 9.2E-13, 5.2E-17, 1.2E-18, close to the minimum values of the algorithm. The convergences of Rosenbrock, Rastrigin, Schwefel and Salomon functions are 1～3 orders of magnitude higher than those of four contrast particle swarm optimization algorithms. At the same time, the convergence of the proposed algorithm is 5%—30% higher than that of the contrast algorithms. The proposed algorithm has significant effects on improving convergence speed and precision, and has strong capabilities in escaping from the local extremum and global searching.

fuzzy membership degree; Gaussian learning; particle swarm; differential evolution; fusion optimization

2017- 03- 06;

2017- 04- 24。

国家自然科学基金资助项目(61603304, 61690211)。

周伟(1974—)，男，上海人，副教授，博士研究生，主要研究方向：飞行器总体设计与多学科优化； 罗建军(1965—)，男，陕西西安人，教授，博士，主要研究方向：航天器制导与飞行控制； 靳锴(1988—)，男，河北石家庄人，博士研究生，主要研究方向：再入飞行器、航天器轨迹优化； 王凯(1975—)，男，河北邢台人，副教授，博士，主要研究方向：电力电子网络设计与优化。

1001- 9081(2017)09- 2536- 05

10.11772/j.issn.1001- 9081.2017.09.2536

TP301.6; TP18

A

This work is partially supported by the National Natural Science Foundation of China (61603304, 61690211).

ZHOUWei, born in 1974, Ph. D. candidate, associate professor. His research interests include aircraft system design and multidisciplinary optimization.

LUOJianjun, born in 1965, Ph. D., professor. His research interests include spacecraft guidance and flight control.

JINKai, born in 1988, Ph. D. candidate. His research interests include reentry vehicle system, spacecraft trajectory optimization.

WANGKai, born in 1975, Ph. D., associate professor. His research interests include design and optimization of power electronic network.