谐波谐振的s域模态分析法

张仁武，帅定新

（1.攀枝花学院交通与汽车工程学院，攀枝花 617000；2.攀枝花学院电气信息工程学院，攀枝花 617000）

谐波谐振的s域模态分析法

张仁武1，帅定新2

（1.攀枝花学院交通与汽车工程学院，攀枝花 617000；2.攀枝花学院电气信息工程学院，攀枝花 617000）

为了减少频率扫描的计算时间，提高计算精度，提出了利用s域模态分析确定谐波谐振频率的方法。通过牛顿-拉夫逊迭代法对电力系统在s域中传递函数极点的求解，可得到电力系统中谐振频率及大小程度等信息。在每次迭代求解过程中，只需更新复频率s值即能确定谐振的幅度等信息，不需要频率扫描，从而节省计算时间并提高计算精度。测试系统分析表明，s域模态分析法对于谐波谐振的分析简单有效，快速准确，是分析谐波谐振及谐振治理的有效工具。

谐波谐振；牛顿-拉夫逊迭代法；复频率；测试；s域模态分析

随着电力电子技术的快速发展，大量具有非线性特性的电力设备如电弧炉、电力机车、变频设备等投入运行，电力系统中的谐波污染、谐振问题也随之越来越严重。谐波谐振是电力系统谐波引起的危害之一，易造成因谐波过电压引发的设备故障问题[1-2]。谐波谐振本质是由系统中的容性元件和感性元件之间频繁的无功功率交换造成。

目前在工业电力系统，如风电系统、电气化铁道、煤矿电力系统等均发生谐波谐振现象[3-5]，但鲜有文献能提出对该现象有效分析并治理的工具[6-9]。目前，研究谐波谐振的方法有3种：①频谱分析，频谱分析对驱动点阻抗进行频率扫描可识别谐振存在及确定谐振频率，但频谱分析不能提供更多有效的谐振信息[10]；②模态分析，模态分析可识别谐振存在并确定谐振频率，进而准确定位出谐波谐振区域、元件敏感度等[11-12]，在电力系统中得到广泛应用；③s域模态分析，s域模态分析不仅能得到全面的谐波谐振信息，而且计算精度与计算时间都优于模态分析。

然而，频谱分析和模态分析均需对频率进行扫描，理论上来说当频率精度提高时，将成倍增加计算量。对于模态分析而言，每次需对节点导纳矩阵进行更新及特征值求解，严重限制了模态分析在分析大型电力网络及频率精度高等场景的应用。节点导纳矩阵在s域中计算时，不需要对每个频率点进行扫描，只需对趋于奇异性的节点导纳矩阵进行迭代计算，求解谐振频率精度高、计算速度快。

因此，本文将s域分析法应用于电力系统的谐波谐振分析，通过建立s域下的系统节点导纳矩阵，利用牛顿-拉夫逊N-R（Newton-Raphson）迭代法进行极点/零点的求取，从而确定系统的并联/串联谐振频率及谐振幅度。

1 电力系统s域模型

1.1 s域的节点导纳矩阵

对某个电力网络，可建立关系式为

式中：Y（s）为电力系统的s域节点导纳矩阵；x(s)为广义状态空间；u（s）为系统的输入；y（s）为系统的输出；B和C分别为与u（s）和x(s)维度匹配的系数矩阵。

为便于分析网络对于某个节点注入电流量的响应，可通过式（1）和式（2），得到特定的单输入单输出系统的关系式

式中：b为行向量，其第j个元素为1，其余元素为0；c为行向量，其第i个元素为1，其余元素为0；uj表示系统在第j个节点的注入电流。当在系统的节点j注入电流时，可得节点i的输出电压，则输入阻抗为

输入阻抗Zij（s）代表节点i对节点j的互阻抗，其物理意义是节点i对节点j的影响。

1.2 s域模型以及关于s的导数

节点导纳矩阵Y（s）是对电力系统的结构及参数特性的描述，电力系统中的元件可分为RLC元件、传输线路、变压器等元件。

系统的大部分元件可等效为如图1所示的RLC串联或并联的形式。通过在时域中的拉普拉斯变换，可得出电阻、电感、电容在s域中的模型。

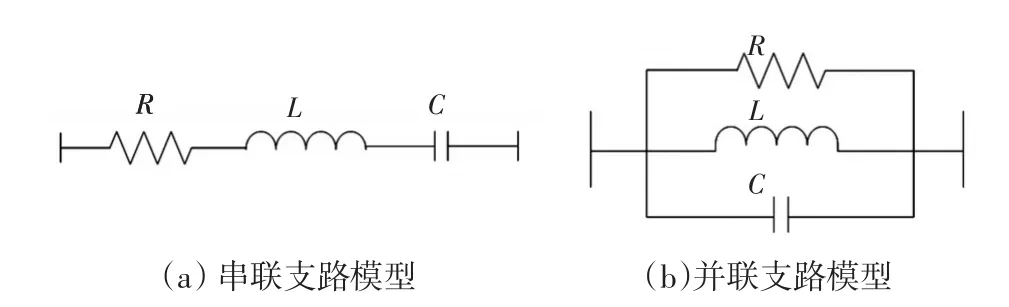
图1 RLC支路模型Fig.1 Model of RLC branch

串联RLC支路以及并联RLC支路的复频域导纳模型为

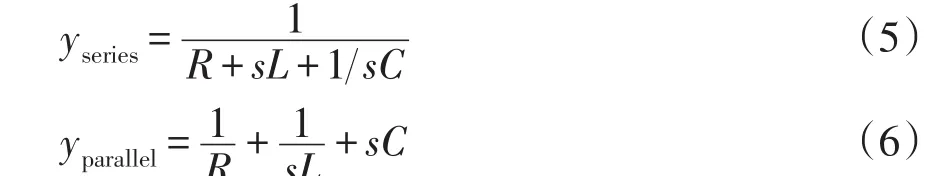
式（5）和式（6）关于s的一阶导数分别为

对于分布参数传输线路模型而言，可等效为图2的π模型线路，π模型的阻抗和导纳分别为

式中：l为单位传输线路长度；γ为传输线路传播常数；Yc为传输线路特征导纳。Ys应被加入到Y（s）对角线元素中；而Yp的负值应被加入到Y（s）的非对角线元素中。传输线路的导纳函数是关于单位传输线路长度l、传输线路传播常数γ、传输线路特征导纳Yc的函数。在单位长度下的传输线路传播常数γ以及传输线路特征导纳Yc分别为为单位长度的传输线路阻抗，Yu为单位长度的传输线路导纳。

图2 传输线路等效π模型Fig.2 Equivalent π model of transmission line

Ys、Yp中线路导纳Yc关于s的一阶导数为

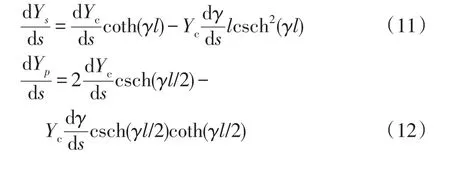
2 电力系统传递函数极点计算

由定义可知系统的极点与系统输入输出无关。故令系统输出yi=1，系统输入uj=0，由式（3）得系统传递函数为

式中，G(s)为系统的二阶传递函数。

将式（13）运用N-R迭代法进行迭代，可得

式中：λ为系统传递函数G（s）的极点；k为迭代次数；Δλ为λ的增量，即

将系统传递函数G（s）及其导数代入式（14）中，可得迭代增量Δλ为

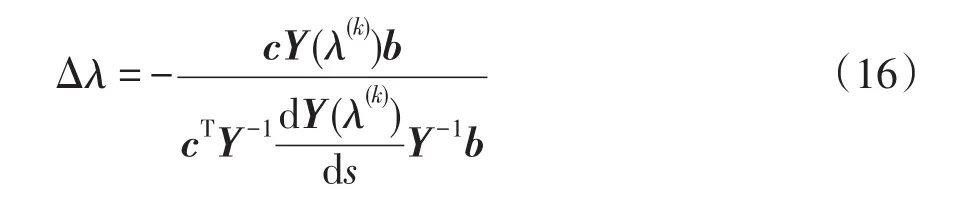
通过式（1）、式（2）表示的简单线性系统，可求出式（16）中的cTY-1与Y-1b分别为

将式（17）、式（18）代入式（16）中经运算，可得

式中：λj为已找到的极点；Rj为对应的留数（j为已找到极点的指数）。

若所求解的极点为重极点或者多重极点，则式（21）可表达为

需要注意到的是在N-R迭代法过程中，当Δλ小于某个给定误差（如10-6）时，则停止迭代，否则更新λ，继续迭代，直到满足迭代精度要求为止。迭代初值的选取对迭代的快慢以及迭代的收敛有着重要的关系，根据文献[13]提出的方法，可消除初值对迭代的影响。为消除已求出极点对迭代的影响，在每一次迭代过程中，可先将已求出的极点滤除，再继续迭代求解，即

式中：m为多重极点个数，m＞1；Rm为传递函数的留数。

再通过式（16）～式（19）的计算，可以得出修正后的迭代增量Δλ为

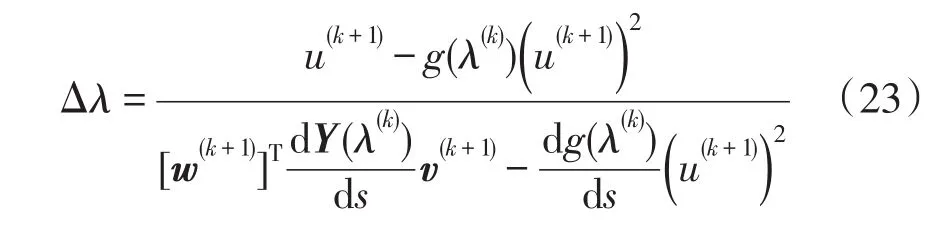
传递函数的留数，根据定义，可得

将式（23）迭代求出的值代入式（24）中，有

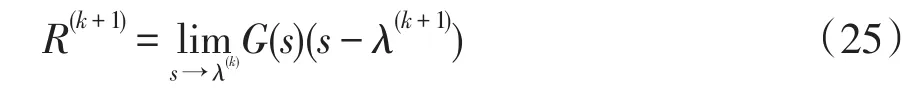
化简为

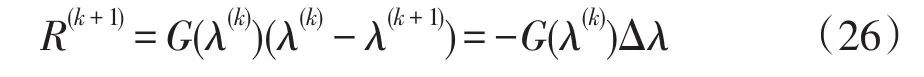
由式（23）可求出传递函数的留数，即谐振幅度为

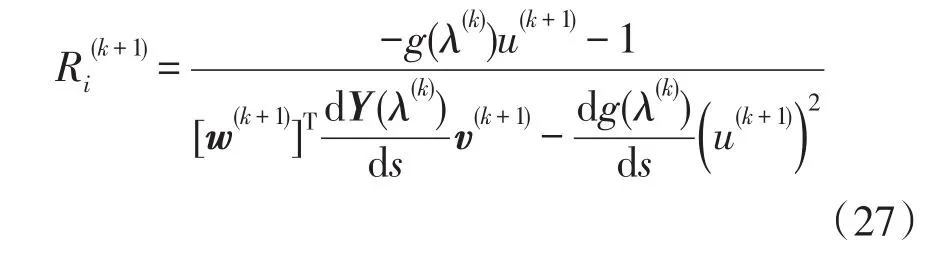
3 算例验证

3.1 三母线测试系统

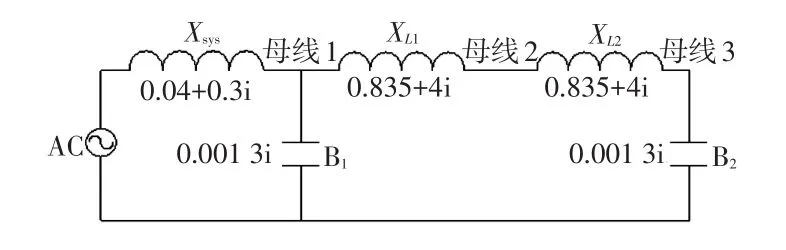
图3 三母线测试系统Fig.3 Three-bus test system

图4 测试系统频谱分析结果Fig.4 Spectrum analysis results of the test system

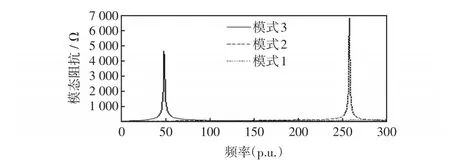
图5 三母线测试系统模态阻抗Fig.5 Modal impedances of the three-bus test system

表1 测试系统模态分析结果Tab.1 Modal analysis results of the test system

对图3的三母线测试系统分别使用文中所提到的3种方法进行谐波谐振分析。系统中的3条母线可被激励产生或观察到谐波谐振。通过对母线2注入1 p.u.的电流，得到如图4的频谱分析。虽然频谱分析可得出测试系统的谐振频率，但难以确定每条母线所对应的谐振频率，也即无法定位具体谐振位置。对测试系统进行模态分析可得出图5及表1，通过模态分析可知母线1的谐振频率为51.8 p.u.，母线3的谐振频率为9.8 p.u.。最后对测试系统进行s域模态分析，通过N-R迭代计算可得测试系统传递函数极点值，对极点值进行处理（虚数部分除以2π）可得测试系统谐振频率及谐振位置，如表2所示。在N-R迭代求解极点计算过程中，极点所对应的留数也可一同求出，留数可以表征谐振幅度，这说明s域模态分析可确定更多的谐振信息。虽然模态分析可得出测试系统的谐振频率和谐振位置，但由于模态分析需对频率一一扫描，耗时较长，共耗时0.14 s，而s域模态分析共用时0.001 6 s，耗时明显少于模态分析所用时间。测试系统只含有三母线，当分析多母线系统时，s域模态分析在计算时间上的优势会更加明显。

表2 三母线测试系统极点计算Tab.2 Calculation of poles in the three-bus test system

3.2 测试系统

为了验证s域模态分析方法的性能，本文用如下的测试系统进行s域模态分析。图6为一典型的工业电力系统，基本的网路结构和线路参数均摘自IEEE Standard 519—1992[14]。电力系统中每一个输出负载都并联了功率补偿电容，而电容会引起谐波谐振。图6所示的电力系统，可由文中前述的建模方法建立等效电路。

图6 五母线测试系统Fig.6 Five-bus test system

系统采用工频50 Hz，系统中各元件的参数在表3中给出，分别为变压器T1等效电感和电阻，L1以及R1分别为输出负载端的等效电感和电阻。

表3 测试系统参数Tab.3 Parameters of the test system

由模态分析法，可得出测试系统在频率范围1～250 Hz内有4个谐振峰值，如图7所示，母线1的谐振频率为143 p.u.，母线2的谐振频率为16 p.u.，母线3的谐振频率为65 p.u.，母线4的谐振频率为172 p.u.。由s域模态分析，得出表4及图8。图8是由测试系统传递函数极点值画出，通过图8与图7的对比，可得出s域模态分析得出的谐振频率与模态分析得出的结果比例几乎一致，图8还可揭示出谐振幅度。模态分析所用时间为0.094 s，而s域共用时间为0.015 s，耗时明显减少。

图7 测试系统模态阻抗Fig.7 Modal impedances of the test system

表4 测试系统极点计算Tab.4 Calculation of poles in the test system

图8 测试系统传递函数极点Fig.8 Poles of the test system’s transfer function

4 结 语

通过在s域对电力系统建立节点导纳矩阵，计算传递函数极点求出电力系统的谐振频率并与模态分析法进行对比。结果表明s域的求解方法不仅能够揭示出电力系统谐振信息，并且计算时间明显少于现有的其他方法，这是由于s域模态分析不需要对频率扫描，而是直接对电力系统传递函数的极点进行迭代计算，从而得出电力系统的谐振频率及幅度信息。s域模态分析可用于任何大小、任何拓扑的电力系统谐振分析，在分析多节点的电力系统时，计算时间会大幅度减少，s域模态分析是分析谐波谐振及谐振治理的有效工具。

[1]谷毅，赵玉柱，张国威，等（Gu Yi，Zhao Yuzhu，Zhang Guowei，et al）.关于500 kV东明开关站启动调试期间发生电压谐振的分析（Discussion on voltage resonance occurred in Bao-Ren 5231 transmission line during startup of Dongming switching station）[J].电网技术（Power System Technology），2002，26（12）：71-74．

[2]赵书强，马燕峰，贺春（Zhao Shuqiang，Ma Yanfeng，He Chun）.抑制谐波的配电网无功优化规划（Reactive power optimal planning of distribution network with harmonic mitigation）[J].电网技术（Power System Technology），2004，28（6）：71-75．

[3]王丽芬（Wang Lifen）.矿井供电系统中谐波与谐振过电压现象分析（Harmonics and harmonic over-voltage analysis in coal mine supply system）[J].煤（Coal），2010，19（7）：102-103．

[4]何正友，胡海涛，方雷，等（He Zhengyou，Hu Haitao，Fang Lei，et al）.高速铁路牵引供电系统谐波及其传输特性研究（Research on the harmonic in high-speed railway traction power supply system and its transmission characteristic）[J].中国电机工程学报（Proceedings of the CSEE），2011，31（16）：55-62．

[5]沈启平，姚骏（Shen Qiping，Yao Jun）.电网谐波条件下双馈感应风电系统改进控制（Improved control of doubly fed induction generator wind turbine with series gridside converter under distorted grid voltage conditions）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（5）：7-13．

[6]葛少云，董佳霖，刘福潮，等（Ge Shaoyun，Dong Jialin，Liu Fuchao，et al）.配电网谐波治理降损效果实证方法（Empirical method of harmonic control loss reduction effect in distribution network）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（3）：1-4．

[7]张杰成，乔鸣忠，朱鹏，等（Zhang Jiecheng，Qiao Mingzhong，Zhu Peng，et al）.滑窗迭代DFT检测谐波和无功电流的新算法（New method of harmonic and reactive current detection based on sliding-window iteration DFT）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2015，27（12）：18-22．

[8]穆子龙，张雨晴（Mu Zilong，Zhang Yuqing）.HVDC系统送端孤岛下谐波不稳定对策探讨（Research on countermeasures to harmonic instability problem at sending end of HVDC transmission system in isolated island operation）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2015，27（4）：33-38．

[9]刘军，黄纯，戴栩生（Liu Jun，Huang Chun，Dai Xusheng）.间谐波检测的快速自适应离散广义S变换方法（Inter-harmonics detection based on fast adaptive discrete generalized S-transform）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2015，27（7）：13-17，29.

[10]Huang Zhenyu，Xu Wilsun，Dinavahi V R.A practical harmonic resonance guideline for shunt capacitor applications[J].IEEE Trans on Power Delivery，2003，18（4）：1382-1387．

[11]Huang Zhenyu，Cui Yu，Xu Wilsun.Application of modal sensitivity for power system harmonic resonance analysis[J].IEEE Trans on Power Systems，2007，22（1）：222-231.

[12]胡海涛，何正友，钱澄浩，等（Hu Haitao，He Zhengyou，Qian Chenghao，et al）.基于模态分析的全并联AT网动态谐波谐振研究（Modal analysis based research on dynamic harmonic resonance of all-parallel autotransformer traction supply network）[J].电网技术（Power System Technology），2012，36（1）：163-169．

[13]Gomes Sergio Jr，Martins Nelson，Portela Carlos.Sequential computation of transfer function dominant poles of sdomain system models[J].IEEE Trans on Power Systems，2009，24（2）：776-784．

[14]IEEE STD 519—1992，IEEE recommended practice and requirements for harmonic control in electric power systems[S].

s-Domain Modal Analysis Method for Harmonic Resonance

ZHANG Renwu1，SHUAI Dingxin2
（1.School of Transportation and Automotive Engineering，Panzhihua University，Panzhihua 617000，China；2.School of Electrical and Information Engineering，Panzhihua University，Panzhihua 617000，China）

To reduce the calculation time and improve the calculation accuracy of frequency scanning，a method of determining the harmonic resonance frequency is proposed in this paper by usings-domain modal analysis.By using Newton-Raphson method to seek the poles of the power system’s transfer function ins-domain，the proposed method can obtain the resonance frequency and its magnitude of the power system.In each iteration of the solution process，only thesdata of complex frequency needs to be updated to determine the information of resonance（e.g.，amplitude）without scanning the frequency，which saves the calculation time and improves the calculation accuracy.The analysis of a test system shows thats-domain modal analysis is simple，effective，fast and accurate for harmonic resonance，indicating that it is an effective tool for the analysis of harmonic resonance and resonance control.

harmonic resonance；Newton-Raphson method；complex frequency；test；s-domain modal analysis

TM714

A

1003-8930（2017）10-0113-05

10.3969/j.issn.1003-8930.2017.10.019

2016-01-20；

2017-08-02

张仁武（1965—），男，本科，副教授，研究方向为电力系统分析。Email：971903609@qq.com

帅定新（1979—），男，博士，副教授，研究方向为电力电子与电力传动。Email：31775897@qq.com