弧齿锥齿轮铣齿机铣削力建模与切齿试验

石　锐,邓效忠,蒋　闯,付　愉

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.西北工业大学 机电学院，陕西 西安 710072；3.西安理工大学 经济与管理学院，陕西 西安 710054)



弧齿锥齿轮铣齿机铣削力建模与切齿试验

石锐1,邓效忠1,蒋闯2,付愉3

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.西北工业大学 机电学院，陕西 西安 710072；3.西安理工大学 经济与管理学院，陕西 西安 710054)

为了提高铣齿机的切齿性能，提出了一种瞬时未变形切削宽度和厚度的计算方法。根据瞬时未变形切屑面积公式，采用斜角切削理论和材料Johnson-Cook本构方程，计算出剪切区流动应力，构建了展成法粗铣弧齿锥齿轮小轮的铣削力模型。编写出铣削力仿真程序，通过计算分析得出铣削力与切削速度和进给量之间的关系，进行了切齿试验。仿真结果与试验结果基本吻合，验证了所建立铣削力模型的正确性。

弧齿锥齿轮；斜角切削；铣削力模型；仿真；切齿试验

0　引言

随着干切削技术在制造业方面的广泛应用，弧齿锥齿轮的干切削铣削加工逐渐成为弧齿锥齿轮铣削加工的主要发展趋势。实践表明：锥齿轮干切削与传统的湿切加工相比，具有齿面精度好、加工效率高、耗能少以及污染小等诸多优点。切削力一直是干切削技术研究的重点。文献[1]建立了滚刀刮削直齿圆柱齿轮的切削力模型。文献[2]针对圆盘成形铣刀铣削直齿圆柱齿轮的加工过程，分别建立了顺铣和逆铣时的切削力模型。文献[3]建立了拉内直齿的切削力模型。文献[4]建立了运用成形法加工螺旋锥齿轮的高速干切切削力模型。文献[5-6]建立了成形法加工螺旋锥齿轮大轮的切削力模型和变性法粗铣弧齿锥齿轮小轮的铣削力模型。

这些理论模型针对加工弧齿锥齿轮时，切削热和切削变形的变化对切削力的影响鲜有研究。本文构建了一种新的展成法粗铣弧齿锥齿轮小轮的铣削力模型，编写出铣削力仿真程序，通过计算分析得出铣削力与切削速度和进给量之间的关系，揭示了切削热和切削变形的变化对弧齿锥齿轮加工时切削力的影响。进行了切齿试验，将数控系统显示的驱动力矩转化为动态切削力后，与MATLAB仿真的结果进行了对比，验证了所建立铣削力模型的正确性。

1　未变形切屑切削宽度和厚度的计算

1.1瞬时未变形切屑切削宽度和厚度

图1为粗切加工示意图。图1中：i和i+2分别为相邻两外刀切削刃，i+1和i+3分别为相邻两内刀切削刃；Qi和Ni分别为相邻两内刀刃与外锥面的交点；Ai和Mi分别为相邻两外刀刃和相邻两内刀刃的交点；Bi和Ci分别为相邻两刀齿的刀尖顶点。在小轮展成粗切过程中，刀盘和工件之间为线接触，两者位置关系如图1所示。依据文献[6]提出的展成法铣削小轮时接触点到刀尖的距离，瞬时未变形切屑切削宽度可表示为：

s(t)=f(φp(t),φ1(t))，

(1)

其中：s(t)为瞬时未变形切屑切削宽度，mm；φp(t)和φ1(t)分别为t时刻刀盘和工件转角，(°)。

图2为未变形切削厚度。图2中：切削层即未变形切削厚度th；θ为刀盘转角，(°)；R为刀盘半径，mm;fz为每齿齿长方向进给量，mm。在实际切削过程中，刀片切入和切出时切削厚度是变化的。

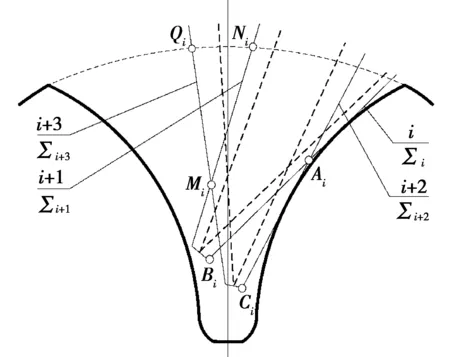
图1　粗切加工示意图

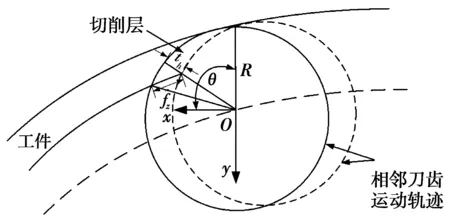
图2　未变形切削厚度

因为刀盘转速远大于轮坯转速，轮坯转速和齿长曲率对未变形切削厚度影响很小，故忽略，则t时刻的未变形切削厚度为：

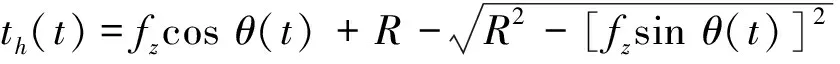
(2)

其中：th(t)为未变形切削厚度，mm；R为刀盘半径，mm；fz为每齿齿长方向进给量，mm。

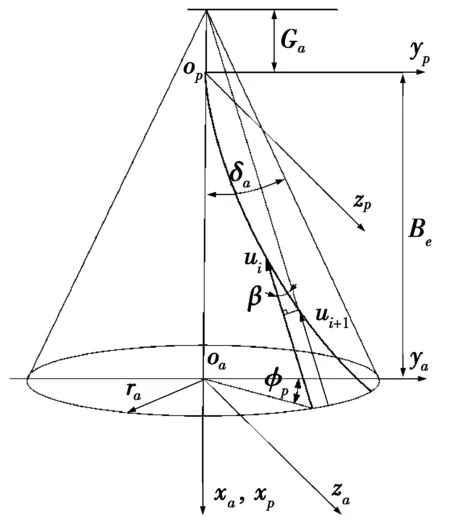
图3　弧齿锥齿轮小轮坐标系

图3为弧齿锥齿轮小轮坐标系。每齿齿长方向进给量fz由弧齿锥齿轮小轮齿面方程中的参数u确定。图3中：Ga为冠顶距,mm；Be为齿宽,mm；δa为面锥角,(°);ra为小轮坐标参数。每齿齿长方向进给量计算公式为：

(3)

其中：β为小轮名义螺旋角，(°)；ui可由任意时刻切削刃i形成的锥面rpi与小轮面锥rpa的交线方程[6]求得：

Lpi(s,θ,φt,φp,u,β)=rpi(s,θ,φt,φp)-rpa(u,φp)=0，

(4)

其中：s为接触点到刀尖的距离，mm；φp和φt分别为t时刻工件和刀盘转角，(°)；θ为刀盘转角，(°)。

1.2瞬时未变形切屑切削宽度与厚度的关系

图4为切屑近似形状。图4中：thn-1、thn和thn+1为相邻时刻的切削厚度；sn-1、sn和sn+1为与厚度同一相邻时刻的切削宽度。根据切齿过程中刀具和工件的相对运动关系推导出的切削厚度和宽度可知，其理论切屑形状应近似于一个四面体，如图4所示，而且与实际切屑相差不多。

图4　切屑近似形状

取同一时刻与s相对应的th，刀片切入至切出之间相邻时刻的瞬时未变形切屑面积互为相似三角形，则刀片切入至切出之间瞬时未变形切屑的切削宽度与厚度的关系为：

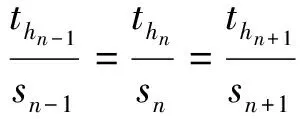
(5)

刀片切入至切出之间瞬时未变形切屑切削宽度随厚度呈等比例变化。可根据厚度的变化计算出非接触点处未变形切屑的切削宽度。由图4可知：未变形切削厚度th最大时，所对应的未变形切削宽度s最大值不一定在接触点处，因此最大切削力不一定在接触点处。

2　铣削力模型

当切削刃的位置发生偏离，不再垂直于切削速度方向，与速度矢量成一夹角，切削过程则由二维切削变成了三维切削，这样的切削过程称为斜角切削。展成法加工弧齿锥齿轮小轮时，工件以一定速度与摇台保持联动关系，刀具与工件的相对速度方向和切削刃呈一定角度，并不垂直，构成斜角切削[7-8]。因此，可把斜角切削理论用于展成法加工弧齿锥齿轮小轮切削力的研究。以下是斜角切削中的几个关键角度关系及转换模型。

2.1斜角切削中的主要角度

图5为剪切平面的角度。斜角切削与直角切削类似，如图5a所示，v为切削速度，φn为法向剪切角，γn为刀具法向前角，th为未变形切屑厚度，tc为切屑厚度。法向剪切角的计算公式[9]为：

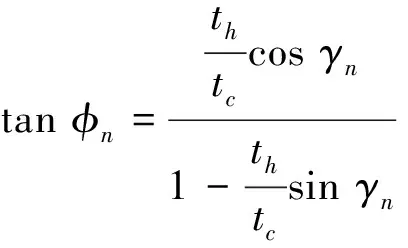
(6)

如图5b所示，剪切流动方向与剪切平面上正交于切削刃的法线方向成一个夹角ηs，其表达式为：

(7)

其中：i为刃倾角；ηc为流屑角。由Stabler法则得知，流屑角ηc和刃倾角i大致相等。

图5　剪切平面的角度

2.2铣削力建模

由斜角切削理论[10]可知，剪切力Fs表示为：

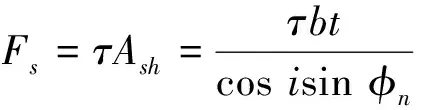
(8)

其中：τ为剪切应力，MPa；b为切削宽度，mm；t为未变形切屑厚度，mm。

依据文献[10-12]的Johnson-Cook本构方程材料模型，得到剪切区内的剪应力分布情况和主剪切面上的剪应力值τ：

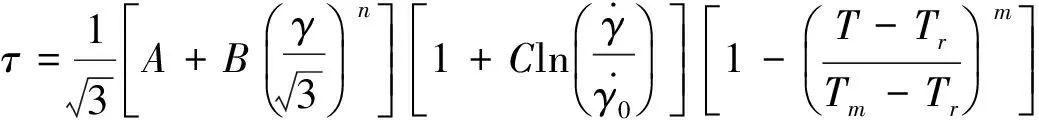
(9)

展成法加工弧齿锥齿轮小轮时，其瞬时未变形切屑面积为三角形，则其外刀剪切力为：

(10)

其中：so为外刀切削宽度,mm；io为外刀刃倾角,(°)；φno为外刀剪切角,(°)。

根据作用在切屑上的力平衡关系，垂直于主剪切面上的正压力Fno为：

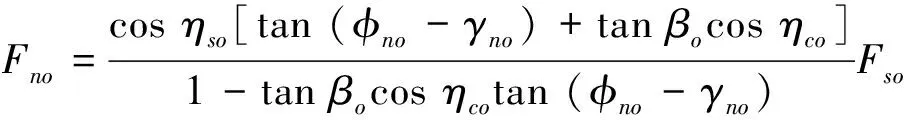
(11)

其中：βo为外刀与切屑面之间的平均摩擦角,(°)；ηso为外刀剪切流动角,(°)；ηco为外刀流屑角,(°)；γno为外刀法向前角,(°)。

假设斜角切削中的法向剪切角同时满足Merchant公式[10]：

(12)

联立式(2)、式(6)和式(12)，即可得到外刀与切屑面之间的平均摩擦角βo：

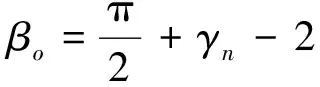
(13)

根据斜角切削理论，外刀切向力Fco、径向力Fro和轴向力Fao，可由剪切平面剪切力Fso和法向力Fno表示为：

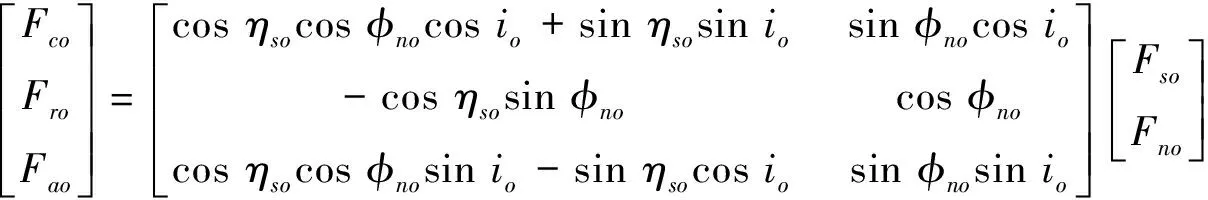
(14)

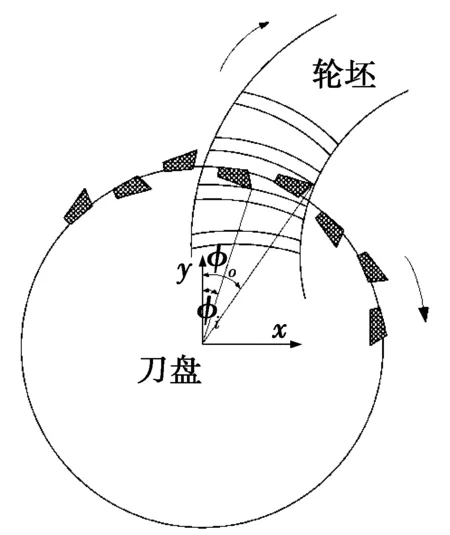
图6　展成法加工示意图

图6为展成法加工示意图。图6中：φo为外切刀盘转角；φi为内切刀盘转角。轮坯和刀盘按一定滚比做展成运动。由图6可知：展成法加工弧齿锥齿轮小轮时，作用在外切刀上的水平、法向和轴向的切削力分量为：

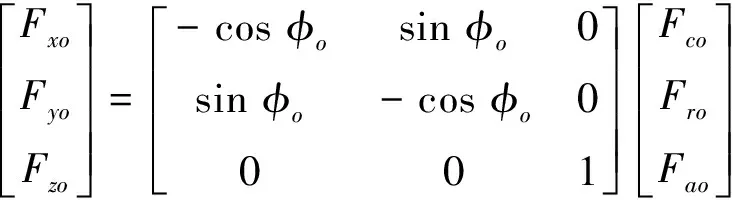
(15)

内切刀切屑与外切刀切屑形状基本相同，因此，同理可得作用在内切刀上的水平、法向和轴向的切削力分量：

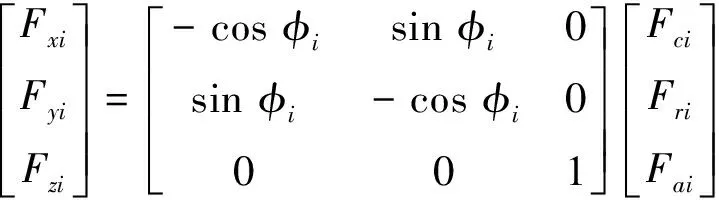
(16)

其中：φi为内切刀盘转角，且满足

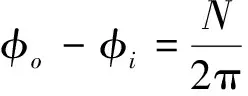
(17)

其中：N为刀盘内外刀片总数。

为了简化所研究的对象，假定铣齿过程中的任意时刻只有一对刀片在参与切削。可知x轴、y轴和z轴内外刀合力为：

(18)

3　计算结果与分析

Step2:据待分割影像Z建立相似图G=(V,E,W )，并计算标准Laplacians矩阵L=I-D-1W；

铣齿机Z轴方向、进给量为8 mm时，分别对切削速度为36 m/min、72 m/min、144 m/min和 288 m/min 进行仿真分析，取在不同切削速度下产生的切削力最大值绘制变化图，见图8。由图8可知：切削速度达到70 m/min左右时，最大切削力达到最大值，此后随着切削速度的增大，最大切削力缓慢下降。

切削速度为70 m/min时，分别对铣齿机Z轴方向进给量为2 mm、4 mm、6 mm和8 mm进行仿真分析，然后，取不同进给量时产生的切削力最大值绘制变化图，如图9所示。由图9可知：最大切削力与进给量呈正比关系。

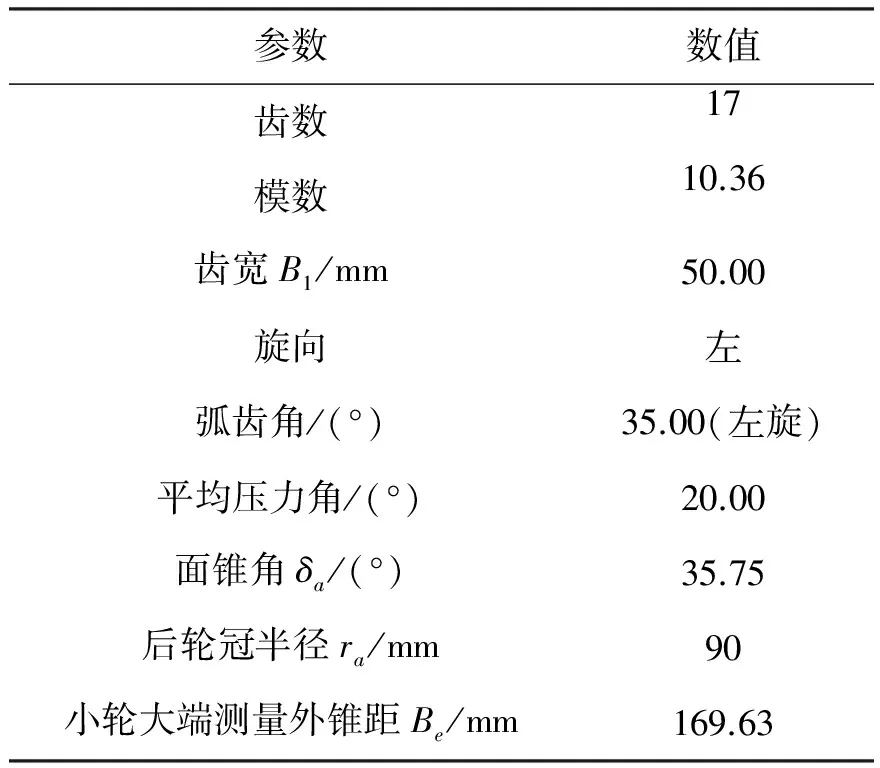
表1　弧齿锥齿轮小轮参数

表2　刀盘参数

图7　铣齿切削力计算流程图

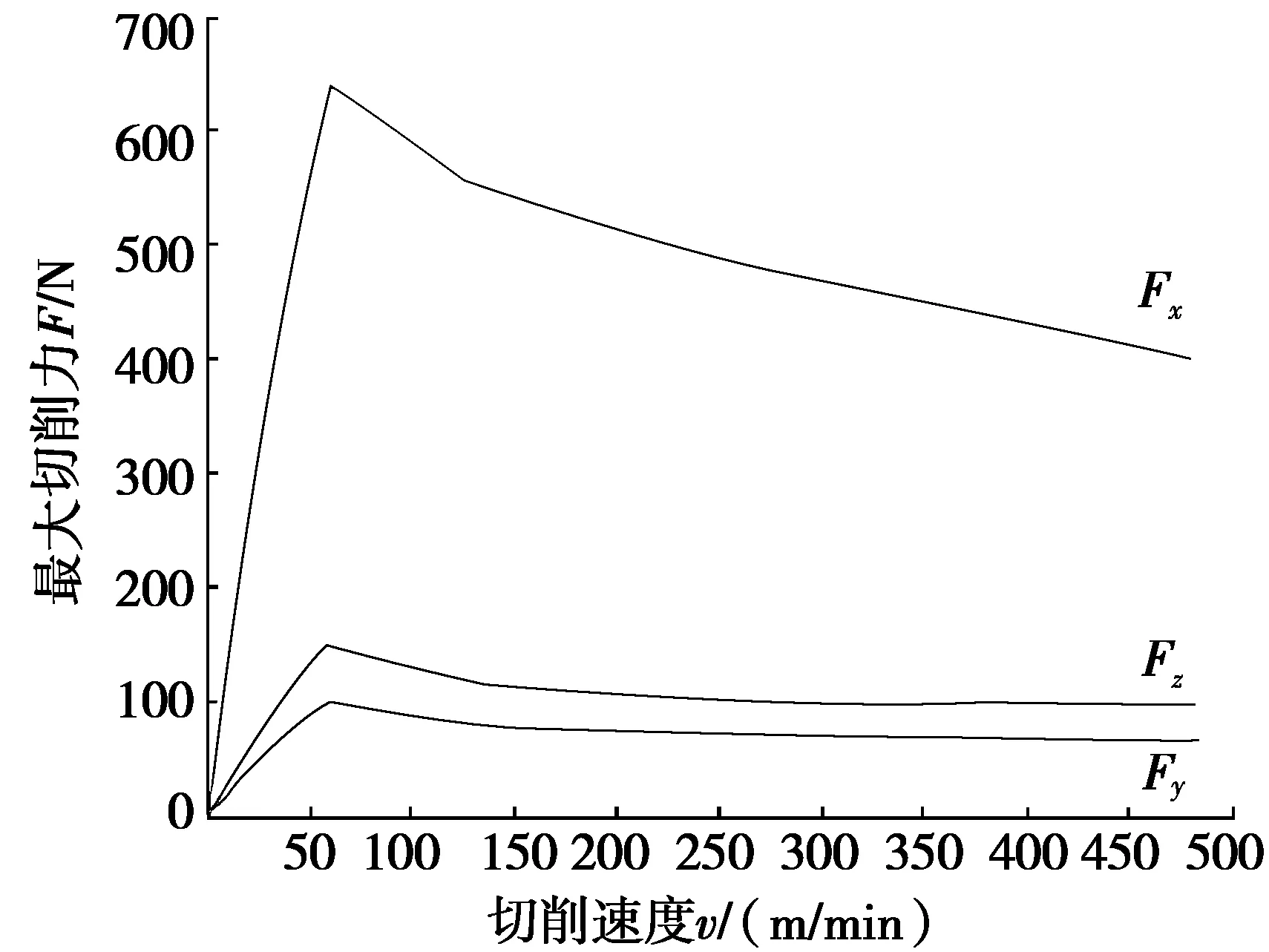
图8　仿真分析中切削速度对切削力的影响

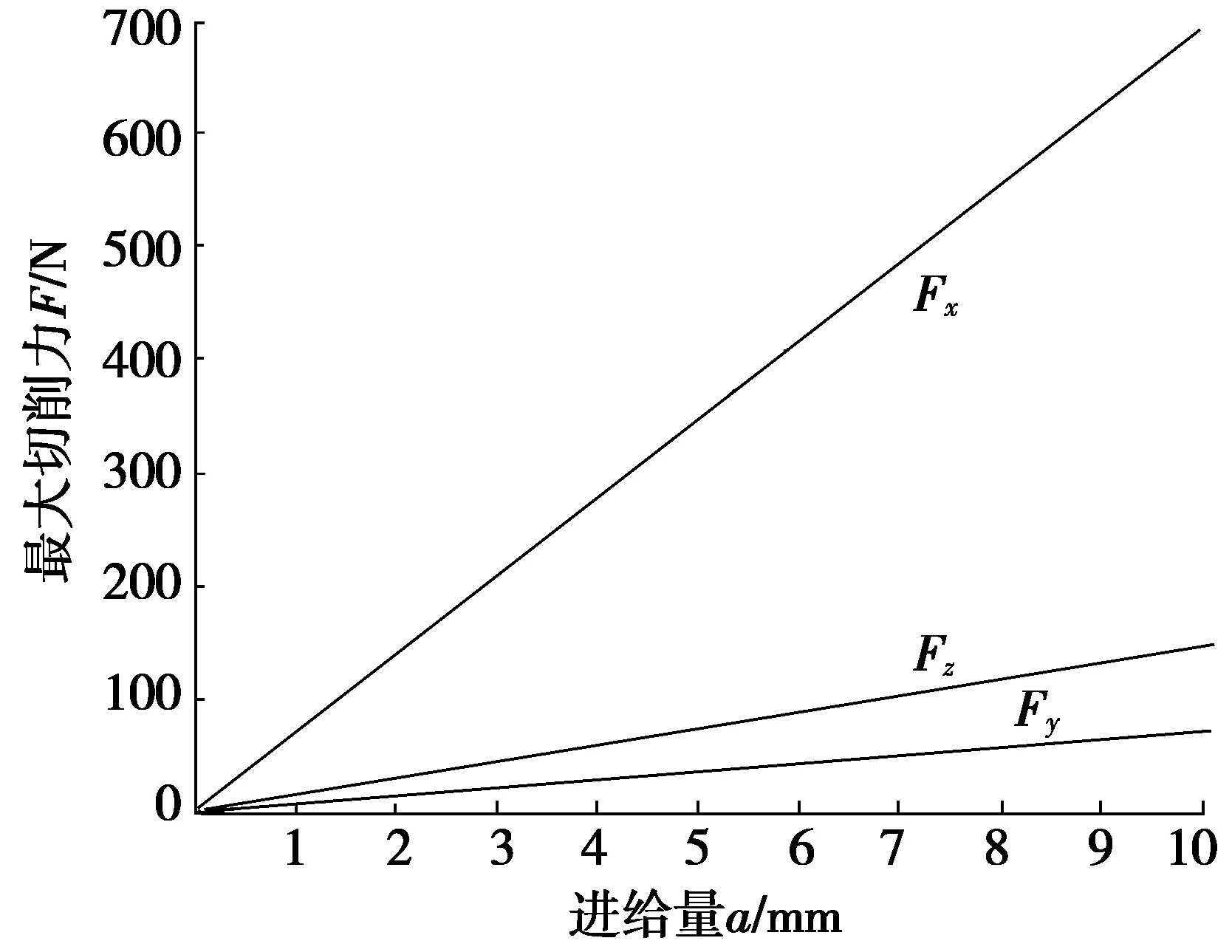
图9　仿真分析中进给量对切削力的影响

4　切齿试验

4.1试验方法

试验采用洛阳科大越格数控机床有限公司自主研发的数控弧齿锥齿轮铣齿机YK2260DX。该铣齿机床最大的两个特点是：刀盘使用17 kW伺服电机驱动；操作系统采用可显示刀盘主轴、工件主轴、纵向进给(X轴)、竖向进给(Y轴)和横向进给(Z轴)伺服电机瞬时转矩的西门子828D数控系统。以上两个特点为验证切削力的理论模型奠定了基础。

切齿试验参照仿真设定的方式进行，切齿加工过程如图10所示。在切齿前，先记录各轴空转时的转矩值。在开始切齿后记录的转矩值减掉空转时的转矩值，才是真正反映切削力产生的转矩。

4.2切削速度对切削力的影响

将不同切削速度下产生的最大切削力数值绘制变化图，见图11。由图11可知：切削速度从60 m/min至70 m/min时，最大切削力增大；切削速度为80 m/min时，最大切削力有小幅减小，这是由于切削速度的提高使剪切区温度降低所致；而当切削速度增大到90 m/min时，最大切削力又有所增大。对比仿真结果，发现切削速度在90 m/min时，试验结果与仿真结果不符，这是由于切削速度的提高增加了刀具的磨损，对最大切削力有影响。但切削速度在70 m/min前后时，试验结果与仿真结果基本相同，证明了仿真结果的准确性。

图10　切齿加工过程图

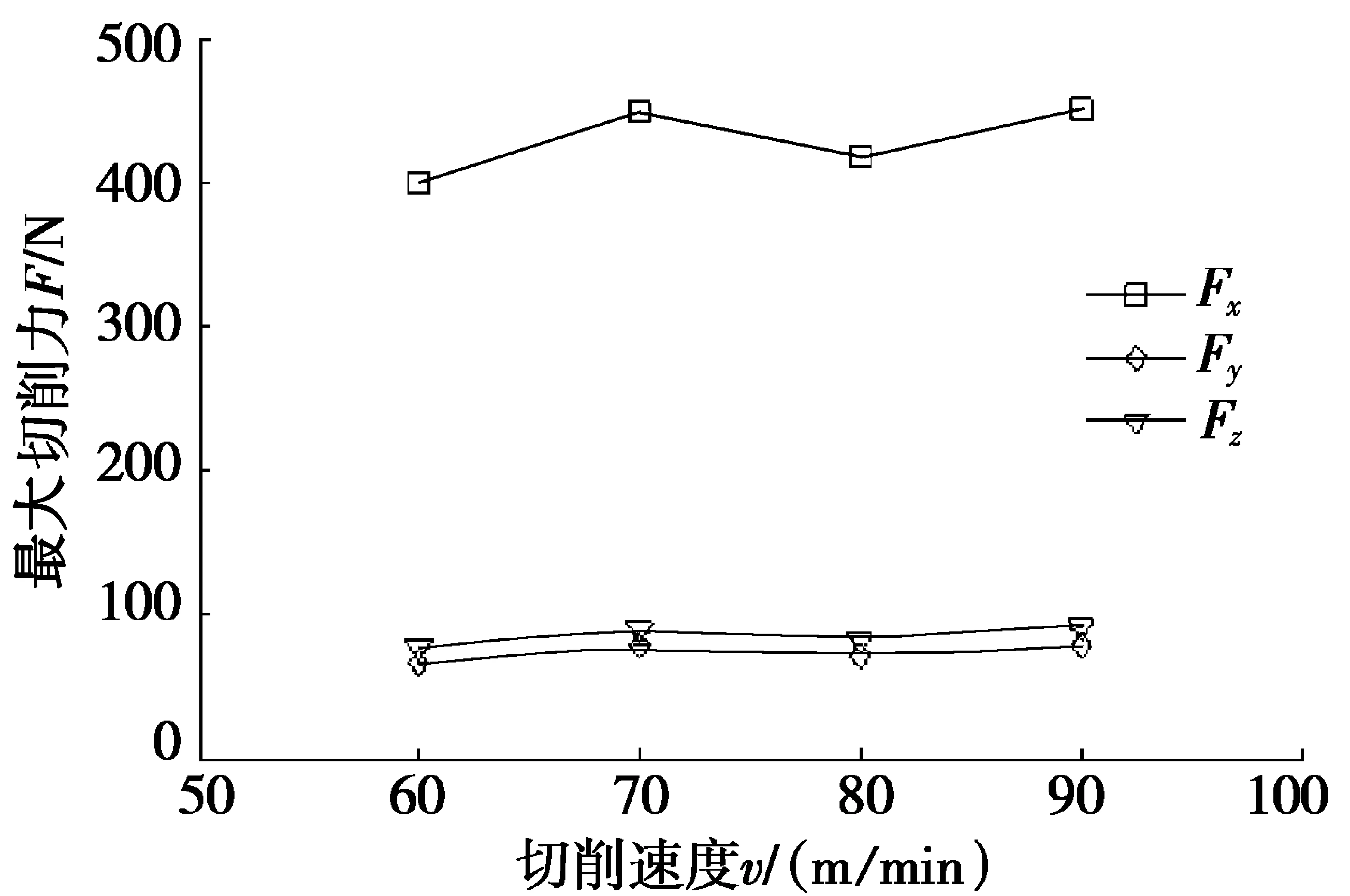
图11　切齿试验中切削速度对切削力的影响

4.3进给量对切削力的影响

图12　切齿试验中进给量对切削力的影响

在切削速度为70 m/min下，分别对铣齿机床Z轴方向进给量为2 mm、4 mm、6 mm和8 mm进行切齿试验。用同样的方法得到不同进给量下瞬时切削力数值。切削前X轴、Y轴和Z轴的转矩值同上。

将不同进给量下产生的最大切削力数值绘制变化图，如图12所示。由图12可知：各轴在不同进给量时的最大切削力随着进给量的增加而增大。对比仿真结果发现：虽然切齿试验过程中切削力与进给量不是呈正比关系，但与仿真结果变化趋势很相似，这是由刀盘径向和轴向安装误差、工件材料不均匀等因素所致。这不影响证明仿真结果的准确性。

5　结论

(1)提出了一种展成法粗切弧齿锥齿轮小轮时的未变形切削宽度和厚度的计算方法。

(2)考虑了切削速度和温度对切削力的影响，建立了展成法粗切弧齿锥齿轮小轮时的铣削力模型。

(3)使用MATLAB编制计算程序，分析了切削速度和进给量对切削力的影响，为加工不同齿轮切削力的计算提供了一定的参考。

(4)根据西门子828D数控系统可显示各轴伺服电机瞬时转矩的特点，进行了切齿试验。将数控系统显示的驱动力矩转化为动态切削力后与MATLAB仿真的结果进行了对比，试验结果与仿真结果基本吻合，验证了所建铣削力模型的正确性。

[1]ANTONIADIS A,VIDAKIS N,BILALIS N.A simulation model of gear skiving[J].Journal of materials processing technology,2004,146(2):213-220.

[2]陈斌,黄筱调,洪荣晶,等.高效盘形齿轮铣刀切削力的研究[J].机床与液压,2009,37(11):4-6.

[3]SUTHERLAND J W,SALISBURY E J,HOGE F W.A model for the cutting force system in the gear broaching process[J].International journal of machine tools & manufacture,1997,37(10):1409-1421.

[4]廖从建,李清.锥齿轮高速干切削力学建模及有限元仿真研究[D].天津:天津大学,2012.

[5]贾新杰,邓效忠,苏建新.成形法加工螺旋锥齿轮铣削力模型[J].农业机械学报,2012,43(12):268-272.

[6]贾新杰,邓效忠,王斌.变性法粗铣弧齿锥齿轮小轮切削力模型[J].中国机械工程,2013,24(18):2515-2518.

[7]张华,韩益南,李天兴,等.等高齿弧齿锥齿轮的三维精确建模与加工试验[J].河南科技大学学报(自然科学版),2015,36(4):27-31.

[8]任小中,胡海峰,董后云,等.磨削工艺参数对斜齿轮磨削温度的影响[J].河南科技大学学报(自然科学版),2015,36(3):9-13.

[9]陈明,安庆龙,刘志强.高速切削技术基础与应用[M].上海:上海科学技术出版社,2012.

[10]SHAW M C.Metal cutting principles[M].Oxford:Oxford University Press,1984:58-62.

[11]ASTAKHOV V P,OSMAN M OM,HAYAJNEH M T.Re-evaluation of the basic mechanics of orthogonal metal cutting:velocity diagram,virtual work equation,and upper-bound theorem[J].International journal of machine tools and manufacture,2001,41(3):393-418.

[12]李炳林,王学林,胡于进,等.斜角切削的热力建模与仿真分析[J].中国机械工程,2010,21(20):2042-2048.

[13]陈刚,陈忠富,陶俊林,等.45钢动态塑性本构参量与验证[J].爆炸与冲击,2005,25(5):451-456.

国家自然科学基金项目(51475141)

石锐(1988-),男,河南安阳人,硕士生;邓效忠(1957-),男,河南洛阳人,教授,博士,博士生导师,主要研究方向为螺旋锥齿轮的设计理论与制造技术.

2016-04-20

1672-6871(2017)01-0015-06

10.15926/j.cnki.issn1672-6871.2017.01.004

TH132.41

A