带有线性饱和治疗函数的SIR模型动力学研究
2017-11-14,
,
(浙江理工大学理学院,杭州 310018)
带有线性饱和治疗函数的SIR模型动力学研究
周康,路秋英
(浙江理工大学理学院,杭州 310018)
推广了一类具有双线性发生率函数和饱和治疗函数的SIR传染病模型,研究了其地方性平衡点的存在性、稳定性及后向分支现象。研究表明:当基本再生数小于1时,若饱和治疗率较小,则系统发生后向分支。同时证明了系统至多存在4个平衡点。
治疗函数;SIR传染病模型;后向分支;基本再生数
0 引 言
传染病模型的研究有助于人们发现疾病的传染规律并对其加以控制。早在1927年,Kermack等[1]提出了著名的SIRS疾病传染模型,其中S代表易感染人群,I代表可将疾病传染给易感者的感染者人群,R代表获得临时免疫的恢复人群。自此,诸多此类研究集中在探索更加符合现实规律的传染病模型及其动力学行为分析,提出了各种形式的发生率函数,如双线性发生率函数λSI[2-3]、饱和发生率函数[4-8]及其他特殊的非线性发生率函数[9]。其他更为一般形式的发生率函数,如kIpS/(1+αIq)[10]或λIpSq[11-12]也已被提出并大量研究。通常地,与经典的双线性发生率相比较,非线性发生率函数更能反映感染者的行为改变和拥挤效应,同时也导致了更加丰富和复杂的动力学行为,如后向分支的发生。基本再生数R0是经典传染病模型判断疾病是否灭绝的一个重要变量。当基本再生数大于1时,疾病可持久存在;当基本再生数小于或等于1时,疾病灭绝。此时系统从无病平衡点到地方性平衡点的分支是向前的。而当后向分支发生时,即使基本再生数R0小于1,模型仍表现出多个地方性平衡点,基本再生数是否小于1不再直接决定疾病可否被消除。
对于疾病传染模型,研究的目的不仅是掌握疾病的发生机制和发展规律,更需要提出有效方案达到控制疾病快速传播进而消除疾病,所以需要在模型中考虑治疗函数。Wang[4]分析了带有如下治疗函数的SIR模型,即
其中:r>0,表示感染者的治疗能力。该治疗函数意味着治疗率与感染者的数量成正比当且仅当治疗能力还未达到最大时,否则将采取最大治疗能力。
本文建立并研究的传染病模型为
其中:A>0为人口的补充率,d>0为自然死亡率,γ>0为自然恢复率,ε>0表示疾病致死率。h(I)为如下改进的治疗函数:
其中:m=rI0+k,代表饱和治疗率;k表示常态下的正常预防能力。
由于第一个和第二个方程与R是独立的,所以此处可以对系统进行降维处理,简化为如下的二维系统:
(1)
本文主要研究系统(1)的后向分支及全局动力学性质,得到了其地方性平衡点的存在性,稳定性及后向分支现象。研究证明:当基本再生数小于1时,若饱和治疗率较小,则系统可发生后向分支;同时证明了系统至多可存在4个平衡点。
当r=k=I0=0时,即文献[13]的情况;当k=0时,即文献[4]的情况。
1 平衡点及后向存在性
首先考虑系统(1)的平衡点。当感染者数量I=0时,系统(1)存在唯一的无病平衡点E0=(A/d,0)。对于地方性平衡点,满足:

(2)
记基本再生数
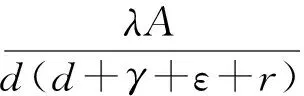
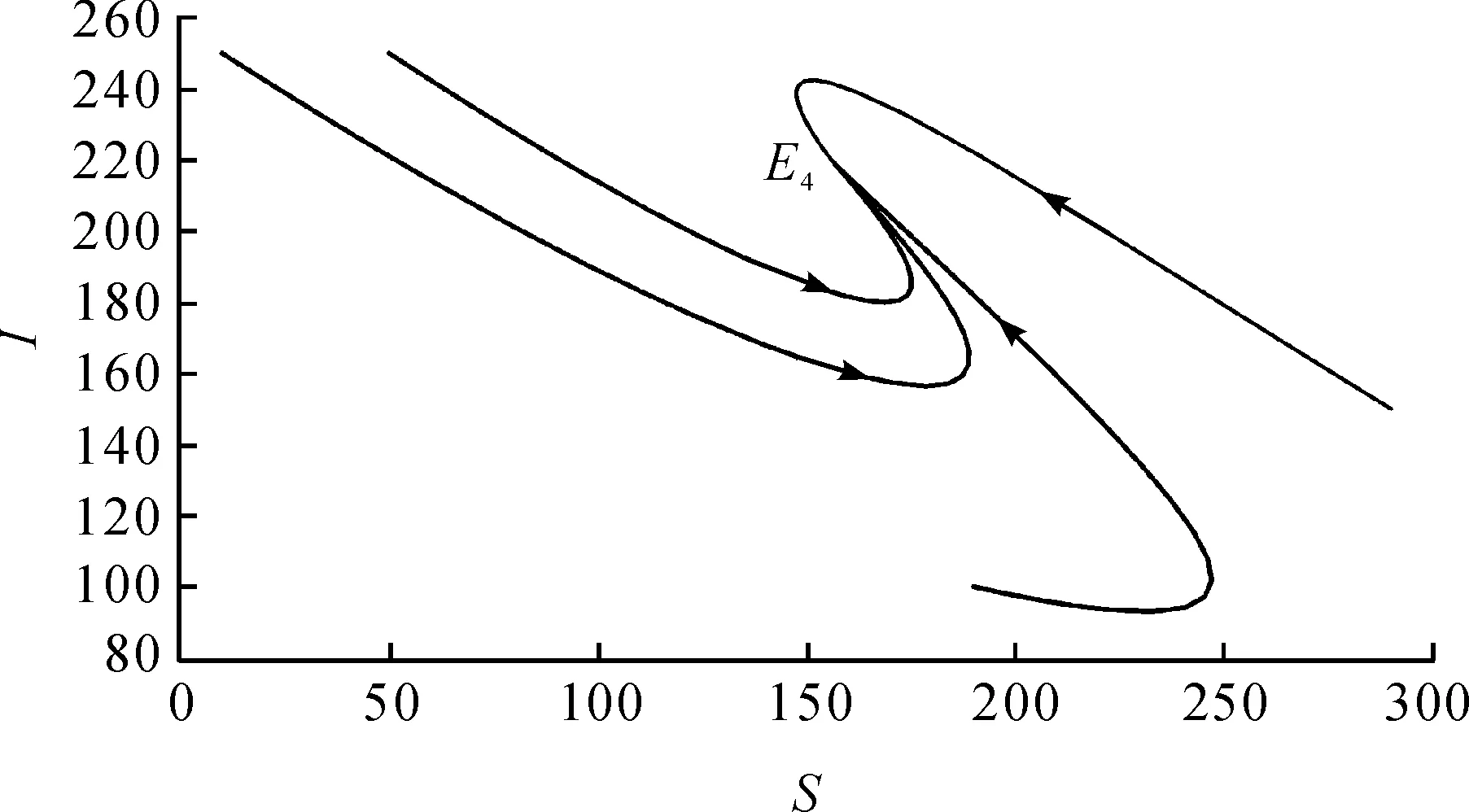
情况1:当0 (3) 由式(3)的第一个方程中求出S=A/(d+λI),将其带入式(3)的第二个方程并化简可得: aI2+bI+c=0 (4) 其中: 则这个方程可能存在正解: (5) 其中 Δ=b2-4ac=[d(1-R0)(d+γ+ε+r)+λk]2- 4λkd(d+γ+ε+r) (6) 从Ii(i=1,2)的表达式可以看出,当b≥0时,显然有Ii<0,故只需考虑b<0的情况。b<0等价于 (7) 容易求得Δ≥0等价于: (8) 或: 可以得到: (9) (10) 由于 情况2:当I>I0时,方程(2)可化为: (11) 对方程(11)的正的地方性平衡点的讨论与方程(3)类似。设方程(11)的两个正的地方性平衡点为E3,E4,可得如下定理: 其中: 证明由定理2的b)即可得到此推论。 注1系统(1)至多存在4个平衡点。 注2系统(1)不可能存在4个地方病平衡点。 首先,讨论E1与E2的稳定性。 令 可得方程(2)的Jaccobi矩阵 (12) 定理3当R0<1时,无病平衡点E0是局部渐近稳定的。若R0>1,则E0是不稳定的。 证明在E0点处,把S=A/d,I=0代入式(12)中可得 求得: =-d+(R0-1)(d+γ+ε+r), =-d(R0-1)(d+γ+ε+r). 显然当R0<1时,有tr(J(E0))<0,det(J(E0))>0,此时E0是局部渐近稳定的。相反,若R0>1,则E0是不稳定的。证毕。 定理4若系统(1)的地方病平衡点E1=(S1,I1)存在,则其为一个鞍点。 将其代入式(12)计算得: Q3=λk2-[(d+ε+γ+r)(2d+ε+γ+r)+2λA]k+ λA2-Ad2-Ad(d+ε+γ+r)。 定理5假定E2存在, a) 若λk>λA-3d2-d(ε+γ+r)-2d3/(ε+γ+r),或 (13) 则E2局部渐近稳定; b) 若 (14) 则E2不稳定。 证明可以计算出 tr(J(E2))=-d-λI2+λS2-(d+γ+ε+r)= (15) 由式(15),当d(2d+γ+ε+r)-λ(A-k)≥0时,tr(J(E2))<0。假设 d(2d+γ+ε+r)-λ(A-k)<0 (16) 当tr(J(E2))=0时,可得 I2=Q1 (17) 由式(5)及Q1的定义可得: 由式(6)知Δ=d2(d+γ+ε+r)2[(R0-1-Λ)2-4Λ]。 将λA-λk=d(d+ε+γ+r)(R0-Λ)以及Δ代入化简可得 (18) 若tr(J(E2))=0不可能,则必有Q2<0,化简可得 (19) 假设: (20) 对方程(17)两边平方并化简可得: λk2-[(d+ε+γ+r)(2d+ε+γ+r)+2λA]r+λA2-Ad2-Ad(d+ε+γ+r)=0 (21) 即Q3=0。由此解得: 由不等式(16)可知: 所以 (22) 因此,tr(J(E2))=0的充要条件为E2存在且条件(20)和(22)均成立。 进一步可以发现: 利用I2与Q1的定义可以得到: 因此, 由条件(19)可知Q2<0,故tr(J(E2))<0,此时E2是渐近稳定的。 经计算,不等式(19)等价于λk>λA-3d2-d(ε+γ+r)-2d3/(ε+γ+r)。注意到 故当tr(J(E2))<0时有式(13)成立,此时E2是稳定的。当tr(J(E2))>0时有式(14)成立,此时E2是不稳定的。证毕。 类似地,可得E3,E4的稳定性: 定理6若E3存在,则其为一个鞍点。 定理7假定E4存在, a) 若λm>λA-3d2-d(ε+γ)-2d3/(ε+γ),或 (23) 则E4局部渐近稳定; b) 若 (24) 则E4不稳定。 定理8无病平衡点E0是全局渐近稳定的当且仅当下列两个条件之一成立: 证明 从而,在定理8的条件下,地方病平衡点不存在。进一步,注意到关于总人口的微分方程为: 则 解得: (25) 定义 则Ω为该模型的一个正向不变集。因此,此模型的动力学行为都在Ω里。由式(25)可知系统(1)的一切正解都是有界的,且非负S轴关于系统(1)是正向不变的,非负I轴排斥系统(1)的正解。由定理3可知当R0<1时,无病平衡点E0是局部渐近稳定的。故通过Poincaré-Bendixson定理的推论,始于Ω中的每一个正解最终将趋于E0。证毕。 a)D连续可微; 则系统(1)不存在极限环。其中: 下面利用引理9的Dulac函数来分析系统(1)的极限环的存在性。 定理10当λk<λA 证明通过系统(1)的第一个方程我们可以看出系统(1)的所有正解都在区域Γ内,其中: 因此,假若系统(1)存在极限环,此极限环也必在Γ中。 取Dulac函数如下: 当0 (26) 故当k 当I>I0时, (27) 本节主要借助Matlab数值模拟验证了系统(1)后向分支发生的正确性。 例1取A=500,d=1,ε=0.01,γ=0.01,λ=0.01,r=4,m=25,I0=6,计算得 图1 当A=500,d=1,ε=0.01,γ=0.01,λ=0.01,r=4,m=25,I0=6时的R0-I图 图2 不稳定鞍点E3与稳定平衡点E4 图3 唯一稳定地方性平衡点E4 现代社会,预料某种疾病的诞生并进行有效预防非常重要,例如肝炎、流行性出血热等传染疾病一旦爆发,人们不仅需要掌握疾病的传染规律,同时需要对疾病开展有效的控制和预防。本文研究了一类带有双线性发生率函数以及饱和治疗函数的SIR传染病模型。该模型提出了常态预防的概念,即在某种疾病还未发生感染的情况下,同样保持固定的治疗率以保证对疾病的有效预防。研究表明,模型至多存在4个平衡点,并给出了各平衡点的稳定性分析。同时,研究发现,当基本再生数小于1且饱和治疗率较小时,模型发生后向分支。因此,通过调整参数控制基本再生数小于1,并不能像其他经典的传染病模型一样消除疾病。此种情况下,需要调整特定的参数使疾病稳定在一个较低的感染者水平。 [1] KERMACK W O, MCKENDRICK A G. Contributions to the mathematical theory of epidemics[J]. Proceedings of the Royal Society of London Series A,1927,115a:700-721. [2] WEI J J, CUI J A. Dynamic of SIS epidemic model with the standard incidence rate and saturated treatment function[J]. International Journal of Biomathematics,2012,5(3):1-18. [3] HU Z X, LIU S, WANG H. Backward bifurcation of an epidemic model with standard incidence rate and treatment rate[J]. Nonlinear Analysis Real World Applications,2008,9(5):2302-2312. [4] WANG W D. Backward bifurcation of an epidemic model with treatment[J]. Mathematical Biosciences,2006,201(1/2):58-71. [5] ZHANG X, LIU X N. Backward bifurcation of an epidemic model with saturated treatment function[J]. Journal of Mathematical Analysis & Applications,2008,348(1):433-443. [6] ECKALBAR J C, ECKALBAR W L. Dynamics of an epidemic model with quadratic treatment[J]. Nonlinear Analysis Real World Applications,2011,12(1):320-332. [7] XIAO Y J, ZHANG W P, DENG G F, et al. Stability and bogdanov-takens bifurcation of an sis epidemic model with saturated treatment function[J]. Mathematical Problems in Engineering,2015,2015(1):1-14. [8] ZHOU T T, ZHANG W P, LU Q Y. Bifurcation analysis of an SIS epidemic model with saturated incidence rate and saturated treatment function[J]. Applied Mathematics & Computation,2014,226(1):288-305. [9] XIAO D M, RUAN S G. Global analysis of an epidemic model with nonmonotone incidence rate[J]. Mathematical Biosciences,2007,208(2):419-429. [10] RUAN S G, WANG W D. Dynamical behavior of an epidemic model with a nonlinear incidence rate[J]. Journal of Differential Equations,2003,188(1):135-163. [11] LIU W M, LEVIN S A, IWASA Y. Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models[J]. Journal of Mathematical Biology,1986,23(2):187-204. [12] LIU W M, HETHCOTE H W, LEVIN S A. Dynamical behavior of epidemiological models with nonlinear incidence rates[J]. Journal of Mathematical Biology,1987,25(4):359-380. [13] WANG W D, RUAN S G. Bifurcation in an epidemic model with constant removal rate of the infectives[J]. Journal of Mathematical Analysis & Applications,2015,291(2):775-793. ResearchonDynamicalBehaviorsofSIREpidemicModelwithLinearSaturationTherapyFunction ZHOUKang,LUQiuying ( School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China) This paper generalizes anSIRepidemic model with bilinear incidence rate function and saturation therapy function. The existence, stability and backward bifurcation of the local equilibrium point were studied. The results showed that when the basic reproduction number is less than 1 and the saturation treatment rate is small, backward bifurcation will happen to the system. Meanwhile, the results proved that four equilibrium points exist at most. therapy function;SIRepidemic model; backward bifurcation; the basic reproduction number 10.3969/j.issn.1673-3851.2017.11.019 2017-06-25 网络出版日期: 2017-10-10 国家自然科学基金项目(11101370);浙江理工大学“521”人才培养计划(11430132521304) 周 康(1993-),男,江苏宿迁人,硕士研究生,主要从事常微分方程与动力系统方面的研究。 路秋英,E-mail:qiuyinglu@163.com O193 A 1673- 3851 (2017) 06- 0874- 07 (责任编辑:康锋)








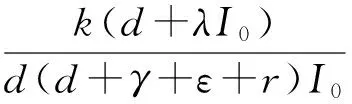
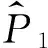

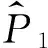
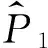


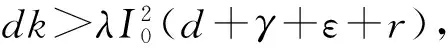
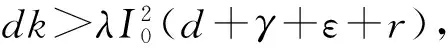


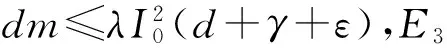
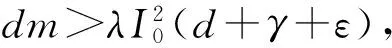







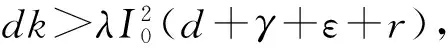
2 平衡点局部稳定性










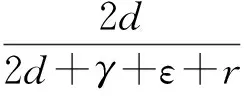
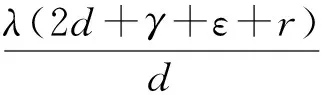







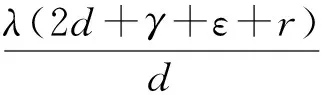


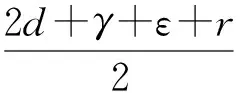
3 平衡点全局动力学
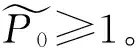


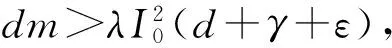





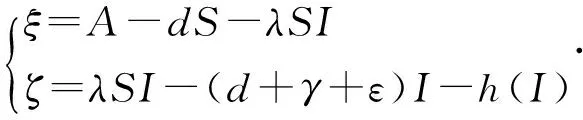
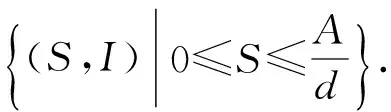
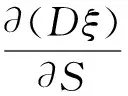
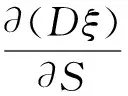
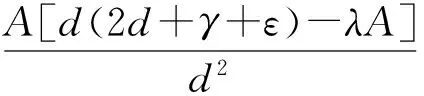
4 数值模拟


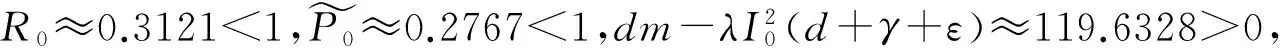

5 结 语
