城市轨道交通环境振动评价指标计算与分析

杜林林， 刘维宁， 刘卫丰， 马 蒙

(北京交通大学土木建筑工程学院， 北京 100044)

城市轨道交通环境振动评价指标计算与分析

杜林林， 刘维宁， 刘卫丰， 马 蒙

(北京交通大学土木建筑工程学院， 北京 100044)

衡量城市轨道交通引起的环境振动水平的指标是最大Z振级和分频最大振级。目前，关于评价指标的计算存在着诸多混淆，影响了评价指标的计算、评价结果,甚至进一步影响线路的规划及设计。通过详细计算重叠系数及计权因子对最大Z振级计算结果的影响，发现当重叠系数达到3/4时，最大Z振级计算结果基本稳定；采用ISO 2631—1:1997中的频率计权曲线更能综合考虑轨道交通引起的环境振动对人体健康、舒适性及工作效率的影响，建议修订《城市区域环境振动标准》(GB 10070—88)时采用此频率计权曲线。针对分频最大振级计算方法中的混淆问题，计算并分析线性平均、峰值保持等方法对计算结果的影响，为保证评价结果的可靠性，建议采用峰值保持法进行计算和评价。

环境振动； 评价指标； 最大Z振级； 分频最大振级

随着线网的不断加密，轨道交通线路不可避免地穿越居民区并对沿线居民的正常生活产生影响[1]。现行的用于评价轨道交通环境振动水平的标准有《城市区域环境振动标准》(GB 10070—88)[2]和《城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准》(JGJ/T 170—2009)[3]，评价指标分别为最大Z振级(VLz，max)和分频最大振级(VLmax)。

根据离散采样数据计算最大Z振级和分频最大振级时，现行标准中没有明确指出相邻两幅计算波形的重叠系数，这将影响计算结果的准确性。在计算最大Z振级时，GB 10070—88仍采用ISO 2631—1：1985推荐的频率计权曲线，该版本的计权曲线所考虑的对象是振动引起的“疲劳-熟练度降低限”，不切合目前轨道交通环境振动引起的人体健康、正常工作及舒适性等问题，较为陈旧，应予以修订。而对于分频最大振级，标准JGJ/T 170—2009中尚未明确指出具体的计算方法，采用分频最大振级进行环境振动评价时，有线性平均、峰值保持等不同的算法，因为计算方法的差异往往造成计算结果的不同，严重影响该指标的合理运用。因此有必要对评价指标的计算方法及影响计算结果的因素进行分析研究。

本文通过计算研究重叠系数对最大Z振级及分频最大振级的影响并给出合理的重叠系数取值，对比研究不同版本计权曲线对最大Z振级的影响，通过计算分析各个方法对分频最大振级的影响，对分频最大振级计算方法的选取给出一定的建议，为城市轨道交通引起环境振动评价指标的准确计算提供参考。

1 城市区域环境振动评价指标

1.1最大Z振级的测试及评价方法

GB10070—88和GB10071—88[4]中指出，为评价城市区域的环境振动水平，测量铅垂向Z振级，采用时间计权常数为1s，采用频率计权范围为1～80Hz[5]，计权因子见GB10070—88。测点置于各类区域建筑物室外0.5m以内振动敏感处，必要时测点置于建筑物室内地面中央。计算时需读取每次列车通过时的最大显示数，每个测点连续测量20次，以20次读值的算术平均值为评价量，然后再与GB10070—88中所给出的标准限值进行比较，以评价环境振动水平。

1.2分频最大振级的测试及评价方法

GB10070—88规定了各种振源下城市区域环境振动测量方法及限值标准，主要用于评价城市交通干线和铁路主次干线引起的环境振动。由于线路分布区域、轨道形式及运营条件的不同，城市轨道交通是一种既不同于城市交通干线又不同于国铁铁路干线的交通网，因此城市轨道交通沿线的振动评价标准应有所不同。为了解决城市轨道交通环境振动的评价问题，文献[3]指出采用分频最大振级作为轨道交通环境振动评价量。在4～200Hz频率范围内对铅垂向振动加速度进行1/3倍频程分析，经计权因子修正后可得1/3倍频程中心频率上的最大振动加速度级，即分频最大振级，其中频率计权因子如表1[6-7]所示，环境振动评价标准限值如表2所示。测点布置要求：与建筑物室内振动限值对应的测点宜布置在建筑物一楼室内，也可布置在建筑物基础距外墙0.5m范围内。每次列车通过时记录分频最大振级作为该次列车通过时的测量值，以每次列车通过时该测点VLmax的算术平均值作为该测点的振动评价量。

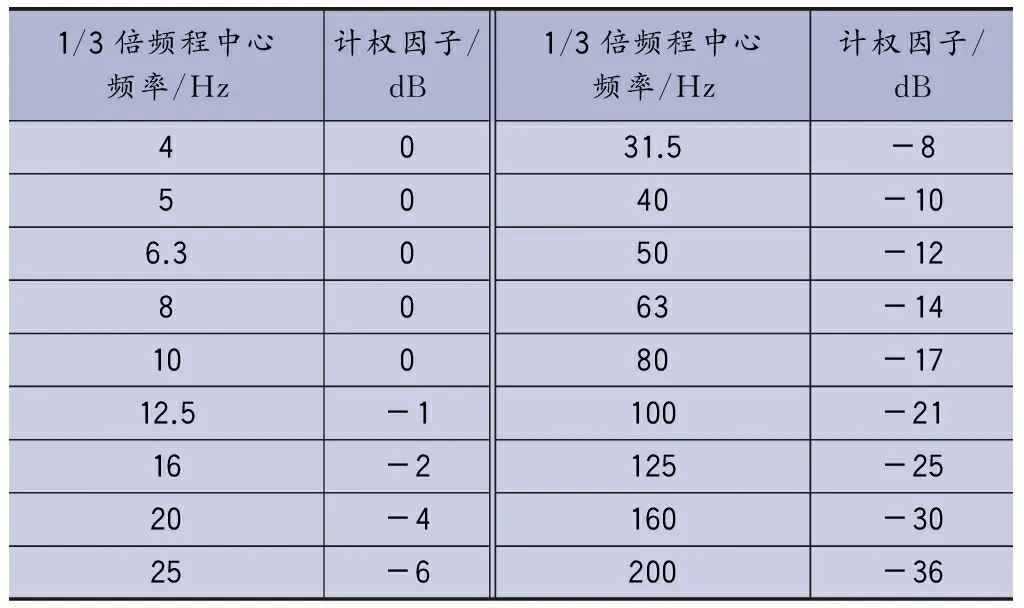
表1 JGJ/T 170—2009加速度在1/3倍频程中心频率的Z计权因子

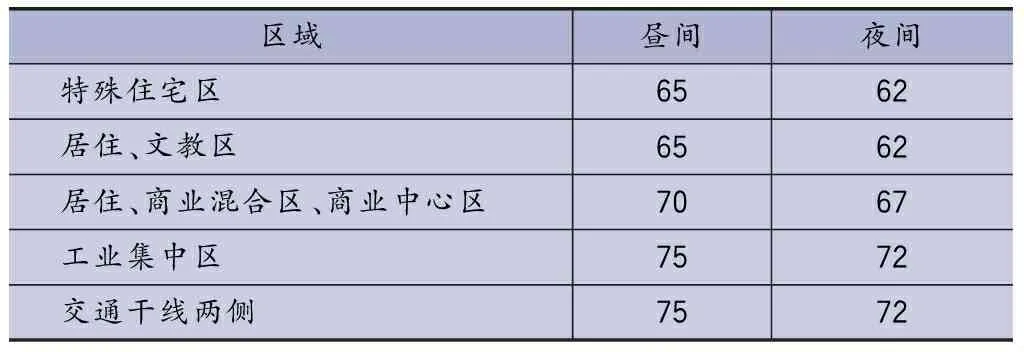
表2 JGJ/T 170—2009建筑物室内振动限值

2 VLz，max和VLmax的计算方法

2.1VLz，max的计算

根据GB10070—88要求采用1s计权，时程信号可依次分为若干幅波形进行分析，对每一幅波形进行1/3倍频程分析得到各个中心频率对应的分频振级,如表3所示。根据式(1)计算可得该幅波形的Z振级，依次计算可得Z振级随时间的变化过程。

VLz=10log(∑10(VLi+αi)/10)

(1)

式中，VLz表示铅垂向Z计权振级，简称Z振级，dB；VLi为1/3倍频程各中心频率对应的振动加速度级，dB；αi为1/3倍频程各中心频率的Z计权因子，dB。具体数值参见文献[1]。

环境振动是随机过程，具有波动性。由数据采集仪获得的数据为离散数据，计算环境振动评价指标时，每次需要计算1s长度的样本数据。为了使得离散数据的计算结果能真实反映连续振动过程，相邻两幅计算波形需要设置一定的重叠率，即重叠系数l以反应客观实际。因而对于离散采样所得的数据，考虑相邻两幅波形间的重叠，并对每幅波形进行计算，计算波形的总幅数n为

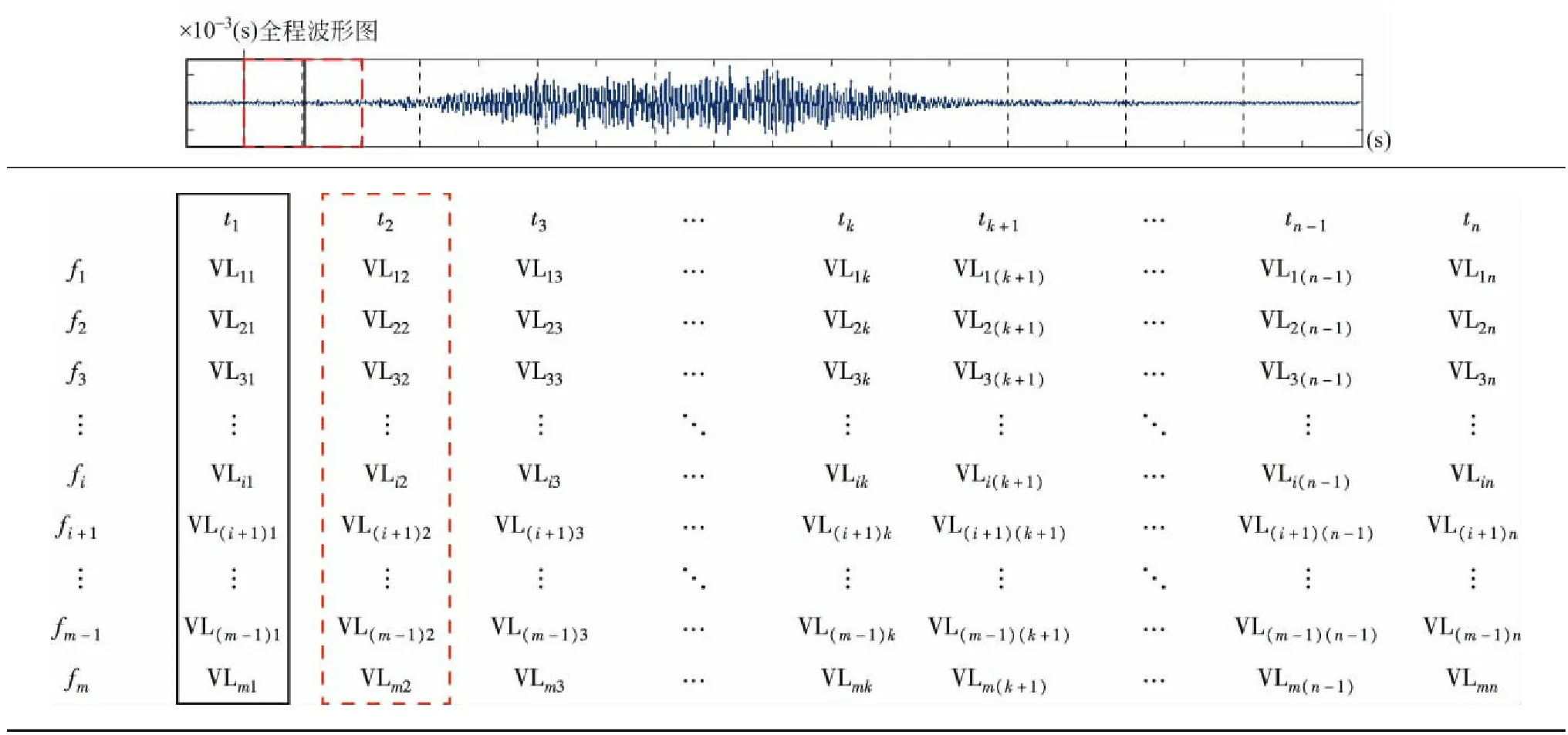
表3 各幅波形分频振级计算示意Tab.3 Diagrammatic sketch of calculating vibration level for each waveform

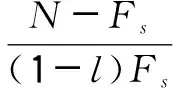
(2)

式中，N为采样点数，Fs为采样频率。

2.2VLmax的计算

JGJ/T170—2009中推荐采用VLmax作为评价指标[8]，却没有明确给出分频最大振级的具体算法，因此在计算VLmax的过程中出现了诸多混淆，影响了环境振动评价结果。针对分频最大振级的计算，常见的方法有线性平均、峰值保持及最大值保持。

线性平均法是指全程分析时计算出每幅波形对应的分频加速度有效值，类似于表3中所示，然后对各中心频率所对应的加速度有效值按式(3)进行线性平均，由平均值求得分频振级值。根据式(4)计算各分频振级并计权求出各分频振级最大值作为分频最大振级。

(3)

(4)

式中，arms，i为1/3倍频程中心频率fi处加速度有效值均值；arms，i，k为第k幅计算波形在1/3倍频程中心频率fi处的加速度有效值；i指1/3倍频程中心频率个数；n指对信号进行分析时，计算的波形幅数总数；a0为基准振动加速度值，取为10-6m/s2。具体数值见表1。

峰值保持即通过对全程每幅波形进行计算可得如表3所示各个时段的分频振级值，按式(5)对各分频求其最大值，即各频段的最大包络值，最后再按式(6)求出分频最大振级。

(5)

(6)

式中，VLi，k表示第k幅计算波形在1/3倍频程中心频率fi处的加速度振级，dB；VLi，max为1/3倍频程中心频率fi处的振级最大值，dB。

最大值保持法是指全程分析过程中，按式(7)找到有效值最大值所对应的一幅波形，对应的时间为tk，对该时段内的数据进行计算可得分频振级最大值。

(7)

式中，arms，k表示第k幅波形对应的加速度有效值；arms，max表示加速度有效值最大值。

3 VLz，max和VLmax的计算与分析

本文选用如图1所示的振动加速度进行计算。该段加速度为地铁列车通过过程中某建筑物一层室外外墙角处铅垂向振动加速度响应。其中，采样频率为1 024 Hz，采样时长为9.8 s，采样点数为10 113。

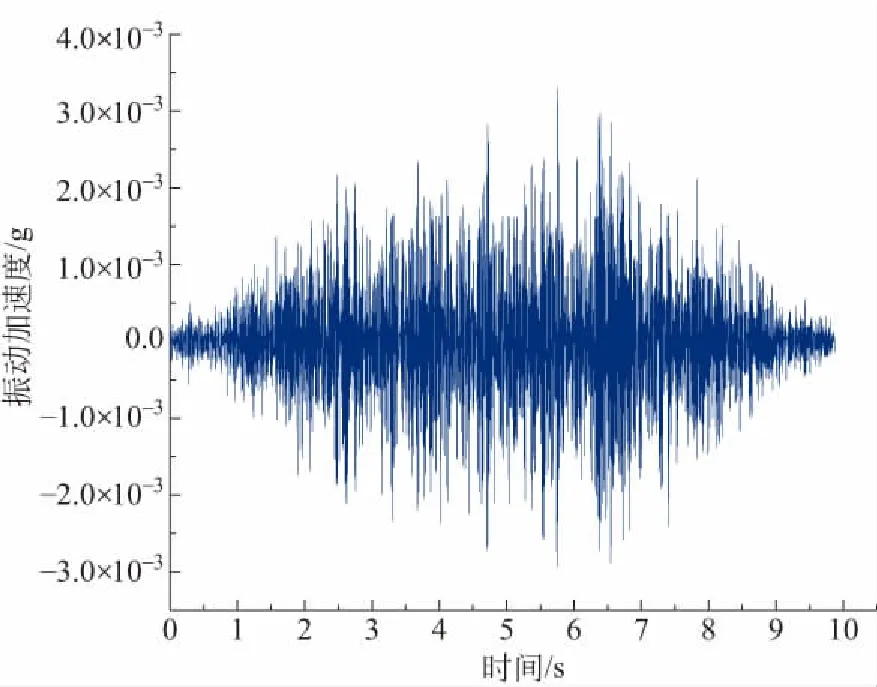
图1 建筑物室外铅垂向振动加速度Fig.1 Vertical vibration acceleration of ground outside the buildings

3.1VLz，max的计算及影响因素分析

Z振级随时间的变化过程如图2所示，由图2可以看出振动强度随时间的变化过程，其中最大Z振级为63.96dB。

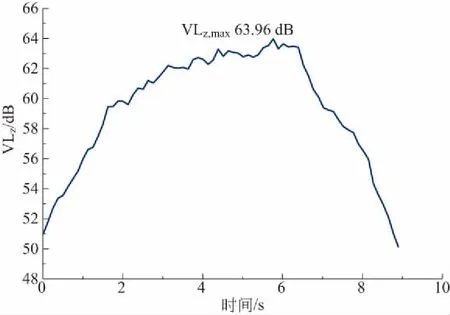
图2 Z振级随时间变化过程Fig.2 Changing process with time of VLz

为了保证计算效率和计算结果的稳定性，分别计算了重叠系数为0、1/2、3/4、7/8时最大Z振级的变化，如图3所示。由图3可知：重叠系数对最大Z振级的计算结果具有一定程度的影响，当重叠系数取3/4时，计算结果是稳定的。

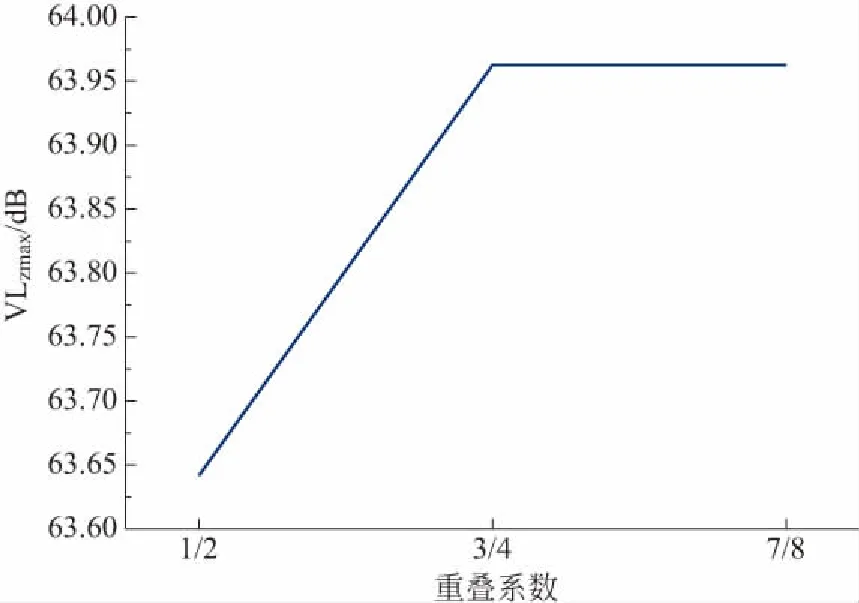
图3 Z振级随重叠系数的变化Fig.3 Changing process with overlapping coefficient of VLz

3.2频率计权曲线对VLz，max的影响

目前，我国《城市区域环境振动标准》(GB10070—88)采用的是ISO2631—1：1985所推荐的频率计权曲线，它是基于等感曲线以及当时采用的“疲劳-熟练度降低限”曲线所得出的，指在一定工作时间下，引起工作者疲劳或熟练度降低的振动值。日本首先将该曲线应用到环境振动标准之中，以评价环境振动对人体的影响程度。“疲劳-熟练度降低限”是一个针对于工业作业人员振动暴露而提出的概念，无法完整地反映出轨道交通引起的环境振动对于人体的影响。对于城市区域轨道交通引起环境振动的评价来说，对象人群主要是建筑物内的人员，他们以坐姿者为多，且坐姿姿势保持的时间一般较长，因此这些人的健康、感觉和舒适性应当着重考虑；而长时间处于立姿和卧姿的人较少，主要关心感觉和舒适度。因此，国际标准化组织在ISO2631—1：1997中提出了新的频率计权曲线[9]，综合考虑了振动对人体健康、舒适度、感觉等的影响，采用新版本的计权曲线更有利于客观真实地进行环境振动评价。

两个版本的频率计权曲线如图4所示，可见，两个版本的频率计权因子在1～4Hz及8～80Hz具有明显的区别。下面通过计算分析计权因子的变化对Z振级计算结果的影响。

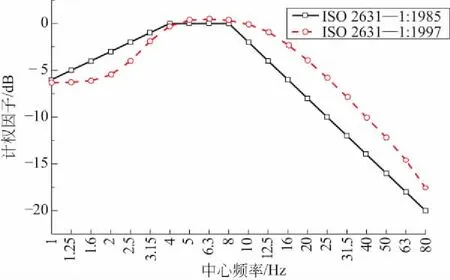
图4 ISO 2631—1：1985和ISO 2631—1：1997频率计权曲线对比Fig.4 Comparing of frequency weighting curves between ISO 2631—1：1985 and ISO 2631—1：1997

图5为采用不同的频率计权曲线时Z振级计算结果，可见：不同计权曲线所得结果的变化趋势一致，反映了列车通过过程中Z振级随时间的变化情况；频率计权因子对于Z振级的计算有着显著的影响，采用ISO2631—1：1997计权值所得计算结果比ISO2631—1：1985计权值大3.3～3.6dB。

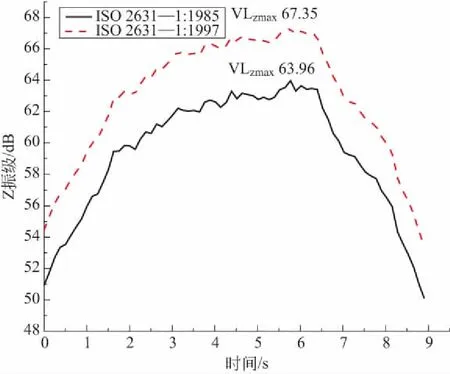
图5 ISO 2631—1：1985和ISO 2631—1：1997频率计权曲线对Z振级计算结果的影响Fig.5 Influence of frequency weighting curves(ISO 2631—1：1985 and ISO 2631—1：1997)on the calculating result of VLz

为了准确反映当前轨道交通引起的环境振动对人体健康、舒适度及感觉的影响，建议对《城市区域环境振动标准》中的频率计权因子进行修改，修改为ISO2631—1：1997中的频率计权曲线。

3.3VLmax的计算及影响因素分析

根据本文第2部分所述，编制程序计算了重叠系数对分频最大振级计算结果的影响，其中时间计权长度取为1s，计算频率范围为4～200Hz，计权因子见表3所示。分别计算了重叠系数为0、1/2、3/4、7/8时计算结果的变化，以峰值保持算法为例，计算结果如图6所示。

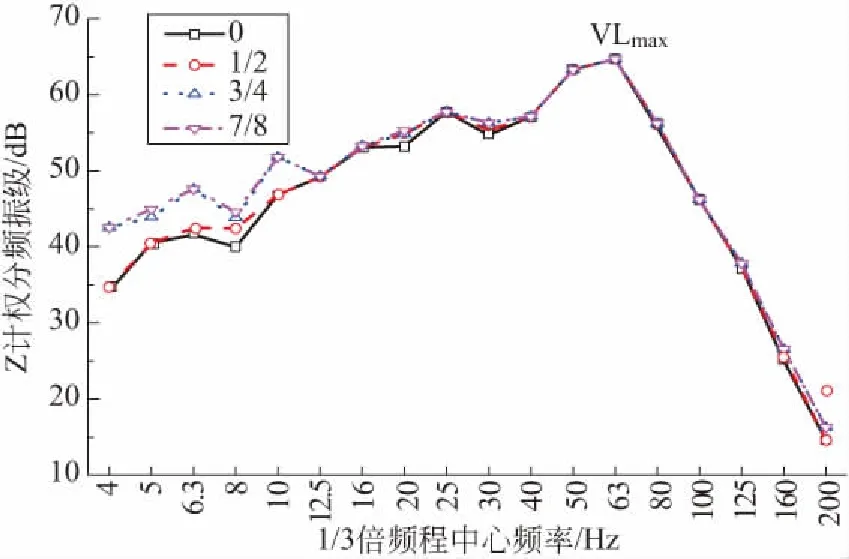
图6 重叠系数对峰值保持算法计算结果的影响Fig.6 Influence of overlapping coefficient on results of peak hold method

观察图6可知，重叠系数对峰值保持计算结果有一定的影响，当重叠系数取为3/4时，计算结果是稳定的。根据计算分析，重叠系数对最大值保持计算结果的影响类似于对峰值保持值的影响，重叠系数为3/4时计算结果是准确的。重叠系数对线性平均计算结果影响较小。综合分析可知，对于分频最大振级的计算，重叠系数取为3/4是合理的。

接下来研究不同计算方法，即采用线性平均、峰值保持及最大值保持对分频最大振级计算结果的影响。重叠系数取为3/4，计算结果如图7所示。

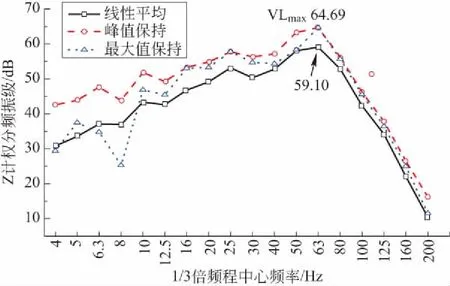
图7 不同算法间Z计权分频振级对比Fig.7 Comparing of Z-weighted vibration level of different calculating methods

由图7可知，不同算法之间存在着显著的差异：1)列车引起的环境振动主要频率成分在20～80Hz之间，其他频率段的响应很小；2)最大值保持与峰值保持在最大值处基本重合，但在低频部分，最大值保持所得计算结果波动性较大，且远低于峰值保持；3)线性平均与峰值保持时所得分频最大振级值相差5.6dB。

根据计算结果，峰值保持算法所得结果代表了最不利的情况，为了实现城市区域安静的轨道交通，为了保证评价结果的可靠性，建议采用峰值保持法作为分频最大振级的计算方法，并用所得计算结果进行评价。

4 结论

1) 重叠系数对VLz，max和VLmax具有一定程度的影响，当重叠系数取为3/4时，计算结果是稳定的，对环境振动评价指标进行计算时，建议重叠系数至少取为3/4；

2) 频率计权曲线对VLz，max具有显著的影响，产生3.3～3.6 dB的计算差，为了准确反映当前轨道交通引起的环境振动对人体健康、舒适度及感觉的影响，建议对《城市区域环境振动标准》中的频率计权因子进行修改，修改为ISO 2631—1：1997中的频率计权曲线；

3) 分频最大振级各个算法之间存在显著的差异，为了保证计算结果的稳定性及评价结果的可靠性，建议采用峰值保持法进行计算和评价。

[1] 袁扬.地铁列车振动环境响应预测的人工单点列脉冲激励方法研究[D].北京，北京交通大学，2014.

YUAN Yang.Study on the artificial single-point pulse excitations method for metro train-induced environmental vibration prediction[D].Beijing， Beijing Jiaotong University， 2014.

[2] 国家环境保护局.城市区域环境振动标准：GB 10070—88[S].北京：中国标准出版社，1989.

National Environmental Protection Agency.Standard of environmental vibration in urban area： GB 10070—88[S].Beijing： Press of China Standards， 1989.

[3] 中华人民共和国住房和城乡建设部.城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准：JGJ/T 170—2009[S].北京：中国建筑工业出版社，2009.

[4] 国家环境保护局.城市区域环境振动测量方法：GB 10071—88[S].北京：中国标准出版社，1989.

National Environmental Protection Agency.Measurement method of environmental vibration of urban area： GB 10071—88[S].Beijing： Press of China Standards， 1989.

[5] 吴永芳.轨道减振效果系统评价方法研究[J].中国铁道科学，2013，34(3)：1-6.

WU Yongfang.Investigation into the evaluation method for vibration damping effect of track systems[J].China railway science， 2013， 34(3)： 1-6.

[6] 中华人民共和国国家质量监督检验检疫总局.机械振动与冲击 人体暴露于全身振动的评价 第1部分 一般要求：GB/T 13441.1—2007[S].北京：中国标准出版社，2007.

International Organization for Standardization.Mechanical vibration and shock-evaluation of human exposure to whole-body vibration—Part 1： General requirements：GB/T 13441.1—2007[S].Beijing： Press of China Standards， 2007.

[7] 中华人民共和国国家质量监督检验检疫总局.机械振动与冲击 人体暴露于全身振动的评价 第2部分：建筑物内的振动(1 Hz～80 Hz)：GB/T 13442.1—2008[S].北京：中国标准出版社，2007.

International Organization for Standardization.Mechanical vibration and shock-Evaluation of human exposure to whole-body vibration—Part 2： Vibration in buildings(1 Hz～80 Hz)： GB/T 13442.1—2008[S].Beijing： Press of China Standards， 2007.

[8] 刘维宁，马蒙.地铁列车振动环境影响的预测、评估与控制[M].北京：科学出版社，2014.

LIU Weining， MA Meng.Prediction， evaluation and control of environmental vibration induced by metro rail transit[M].Beijing： Science Press， 2014.

[9] 卢伟健，姚琨，王世强，等.两个版本的ISO 2631—1频率计权曲线对比[C]//中国环境科学学会学术年会论文集，北京，2009，294-298.

LU Weijian， YAO Kun， WANG Shiqiang， et， al.Comparison of frequency weighting curves in two versions of ISO 2631—1[C]//Proceedings of the Chinese Society of Environmental Science， Beijing， 2009， 294-298.

Computation and Analysis of Evaluation Indicators of Environmental Vibration Induced by Urban Rail Transit

DU Linlin, LIU Weining, LIU Weifeng, MA Meng

(School of Civil Engineering, Beijing Jiaotong University, Beijing 100044 China)

Indicators to evaluate environmental vibration induced by urban rail transit are VLzmax and VLmax. Nowadays, the confusing calculating methods of the evaluation indicators have affected the planning and design of subway lines. The influences of overlapping coefficient and frequency weighting curve on VLzmax are researched in this paper. The study found that the result of VLzmax is basically stable when the overlapping coefficient is 3/4. Frequency weighting curve in ISO 2631-1:1997 is recommended for the amendments to the GB 10070—88StandardofEnvironmentalVibrationinUrbanAreabecause the curve considers the effect of rail transit vibration on human health, comfort and productivity. Calculating methods of linear averaging, peak hold, max RMS hold have significant influences on the VLmax result, which could affect the evaluating result. To ensure the reliability of the evaluation results, peak hold method should be adopted as the calculating method.

environmental vibration; evaluation index; VLzmax; VLmax

10.3969/j.issn.1672-6073.2017.05.007

2016-10-10

2016-10-19

杜林林,男,博士研究生,研究方向为轨道交通环境振动,linlindu07@163.com

国家自然科学基金项目(51378001);中央高校基本科研业务费专项资金资助项目(2015YJS122)

U231.96

A

1672-6073(2017)05-0040-06

(编辑：曹雪明)