喀麦隆曼维莱水电站大波动过渡过程分析
2017-11-13刘国强李永胜
刘国强 李永胜 郭 霄 徐 强
喀麦隆曼维莱水电站大波动过渡过程分析
刘国强 李永胜 郭 霄 徐 强
喀麦隆曼维莱水电站引水系统主要由输水渠道、前池、压力管道、水轮机和尾水管等主要建筑物组成,其水力特性复杂,涉及渠道流的水面线和瞬变流计算分析,以及有压管流的瞬变流计算分析。通过对该电站大波动过渡过程进行模拟分析,为工程设计提供科学的依据以及切实可行的控制和保护措施,确保曼维莱水电站的安全、经济与稳定运行。
瞬变流 水锤 机组转速 真空度
过渡过程广泛存在于水电站引水发电过程之中,是水、机、电系统相互影响的非线性过程,涉及引水发电系统的每一个环节。在水力机组过渡过程中,引水系统的压力尤其是蜗壳末端压力和尾水管的压力、机组的转速等参数都会出现急剧上升或者下降的情况,这种上升和下降对引水系统强度的影响是很大的,因此,结合曼维莱水电站引水发电系统(渠道进水口—输水渠道—前池—压力管道—机组—尾水)布置,有必要开展详细的水力瞬变及过渡过程分析,为工程设计提供科学的依据以及切实可行的控制和保护措施,确保曼维莱水电站的安全、经济与稳定运行。
1 基本理论方法
1.1 基本方程
连续性方程为:
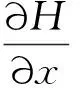
(1)
运动方程为:
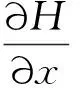
(2)
式中v——管道中的流速,向下游为正;
H——测压管水头;
f——摩阻系数;
x——距离,以管道进口为原点,向下游为正;
t——时间;
a、g——水锤波速和重力加速度;
d、α——管道直径和纵坡角度。
1.2 基本方法
水锤的基本方程(1)和(2)是一组拟线性双曲型偏微分方程,难于直接求出解析解。工程实践中常用特征线法进行近似求解。特征线法的原理是在x-t平面建立一组曲线,沿这组曲线将水锤的偏微分方程转换为常微分方程,这组常微分方程的解就是满足上述曲线所给定的x和t特定关系的偏微分方程的解。
(3)
(4)
式(3)为满足C+正向特征线方程,式(4)为满足C-负向特征线方程。具体参见图1。将式(3)和(4)进行有限差分并整理后可得:
C+:Hp=CB-SBQP
(5)
C-:Hp=CA+SAQP
(6)
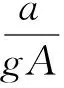
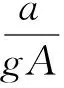
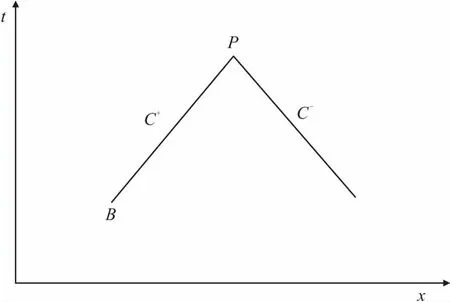
图1 x-t坐标场上的特征线
差分网格见图2所示,有下标A和B者均为已知量,有下标P者为未知量,利用以上二式可解出压头Hp和流量Qp。计算从t=0开始,先求出t=t时各网格结点的H和Q,继而求出t=2t时各网格结点的H和Q,循此前进,直至推求到所要求的时间。
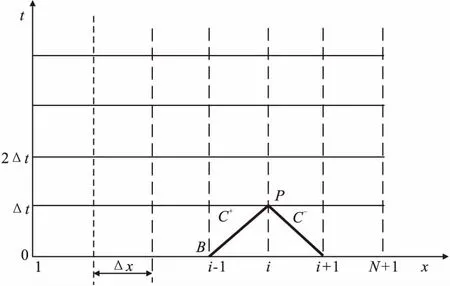
图2 特征线法的计算网格
2 电站概况
曼维莱水电站位于喀麦隆南部紧邻赤道几内亚的恩特姆河上,电站采用引水发电的形式,拟安装4台水轮发电机组,总装机容量为211 MW。电站投入系统后将主要位于基荷运行。电站引水发电系统包括渠道进水口、输水渠道、前池及二道坝、电站进水口、压力管道、厂房及尾水渠。水库正常蓄水位为392 m,最低运行水位为391.5 m。压力管道长约122.6 m,最大引水流量450 m3/s。电站厂房为岸边式地面式,位于恩特姆河峡谷左岸。
3 大波动过渡过程
3.1 计算模型
该电站水力过渡过程的计算简图参见图3,机组负荷变化引起压力钢管水锤波,通过前池反射压力波,引起的前池涌波水位通过连续性方程和运动方程耦合到输水明渠的瞬变流计算。各管段相应参数参见表1。
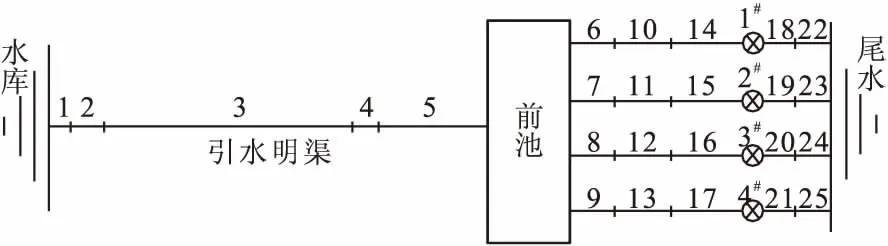
图3 各水力单元计算简图及管道划分
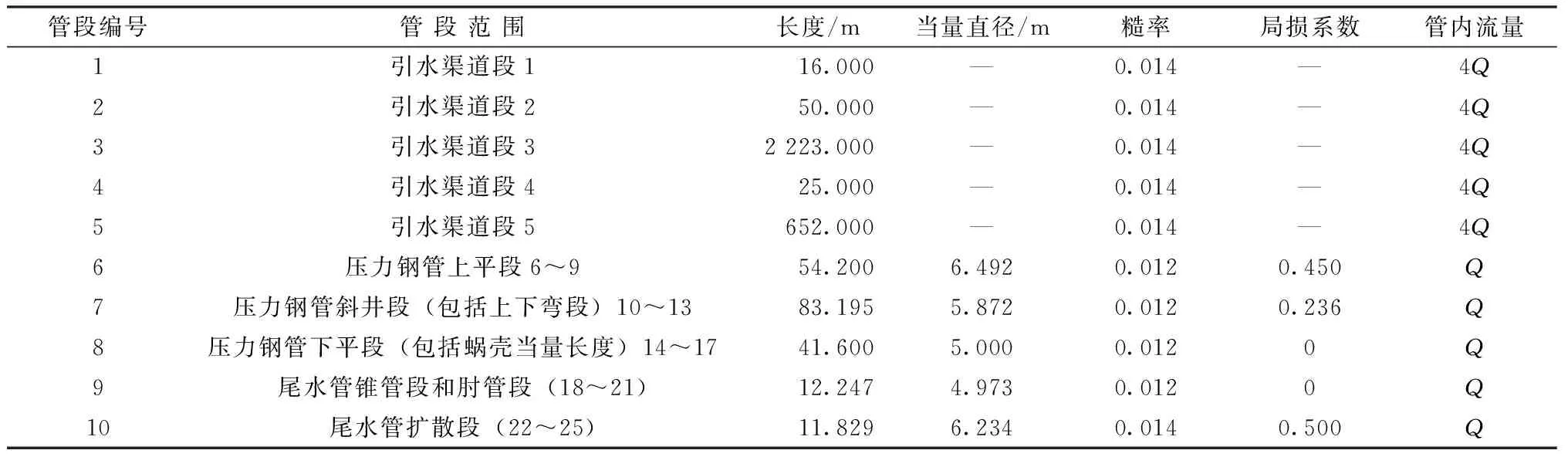
管段编号管段范围长度/m当量直径/m糙率局损系数管内流量1引水渠道段116.000—0.014—4Q2引水渠道段250.000—0.014—4Q3引水渠道段32223.000—0.014—4Q4引水渠道段425.000—0.014—4Q5引水渠道段5652.000—0.014—4Q6压力钢管上平段6~954.2006.4920.0120.450Q7压力钢管斜井段(包括上下弯段)10~1383.1955.8720.0120.236Q8压力钢管下平段(包括蜗壳当量长度)14~1741.6005.0000.0120Q9尾水管锥管段和肘管段(18~21)12.2474.9730.0120Q10尾水管扩散段(22~25)11.8296.2340.0140.500Q
注:计算中为了考虑尾水管和蜗壳水流惯性的影响,采用当量管来代替实际尾水管和蜗壳。
3.2 计算准则
曼维莱电站水轮机额定水头55.0 m,机组额定转速166.7 r/min,调节保证计算标准为:
(3)尾水管进口的最大真空值不大于 8 m水柱。
3.3 计算条件
根据曼维莱水电站引水发电系统的布置以及机组参数,结合电站的运行条件和任务书要求,进行详细的大波动过渡过程计算分析,主要计算条件如下:
(1) 机组导叶关闭规律为TS=5.0 s;机组导叶采用TS=10 s直线开启规律能满足要求;相对开度1对应的机组模型开度为24.7 mm;
(2) 机组转动惯量为6 500 t·m2;
(3) 引水渠道取平均糙率n=0.014,压力钢管取平均糙率n=0.012;
(4) 不出现吸气漩涡的临界淹没深度Scr按戈登(J.L.Gordon)经验公式估算:
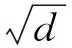
式中Scr——为闸门处洞顶的淹没水深;
c——为经验系数,c=0.55-0.73,对称进水时取小值,侧向进水时取大值;
v——为闸门位置的流速;
d——为闸门处的洞高。计算得临界淹没深度为Scr=5.588 m,对应的前池临界水位为389.588 m。
3.4 计算结果
引水发电子统过渡过程计算成果见表2,工况T1Q主要参数的大波动过渡过程线见图4,工况T1Q对应的明渠沿线各断面水位变化过程线见图5。
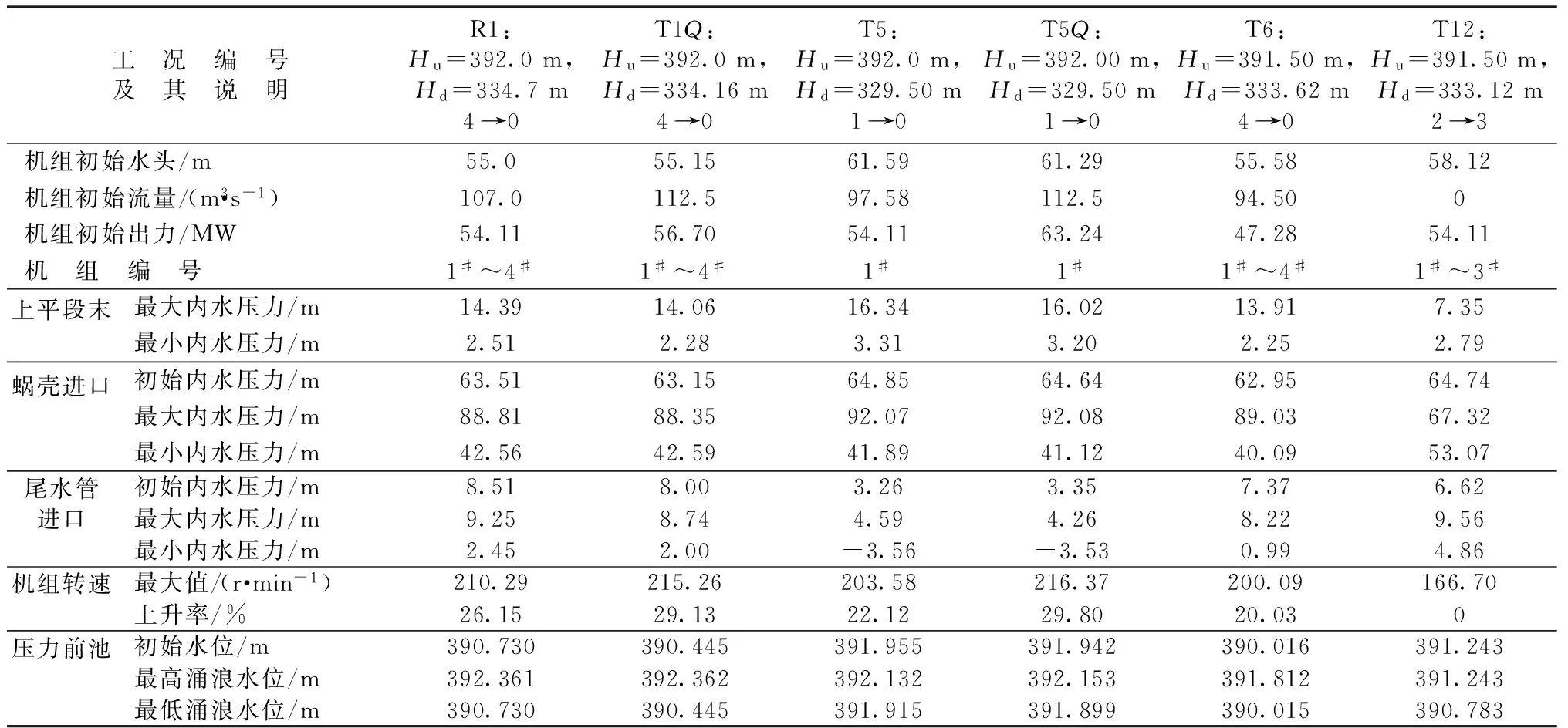
表2 引水发电系统大波动过渡过程计算成果
注:导叶关闭规律(直线):TS=5.0 s,导叶开启规律(直线):TS=10 s;限于篇幅,仅列出部分代表工况,工况编号加字母“Q”表示采用最大引用流量。
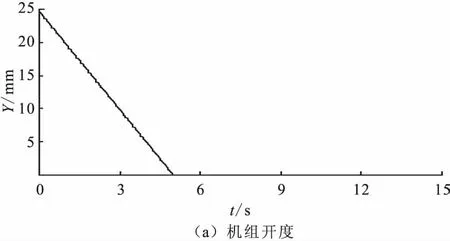
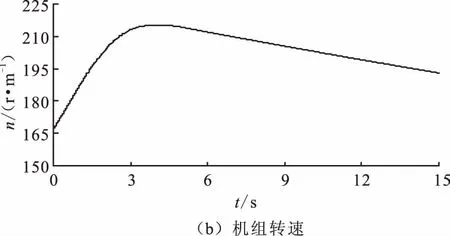
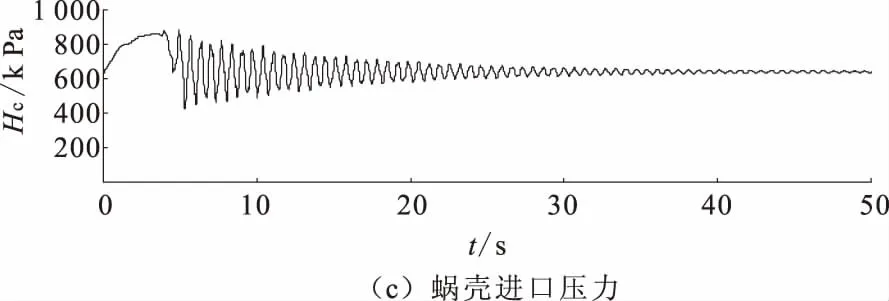
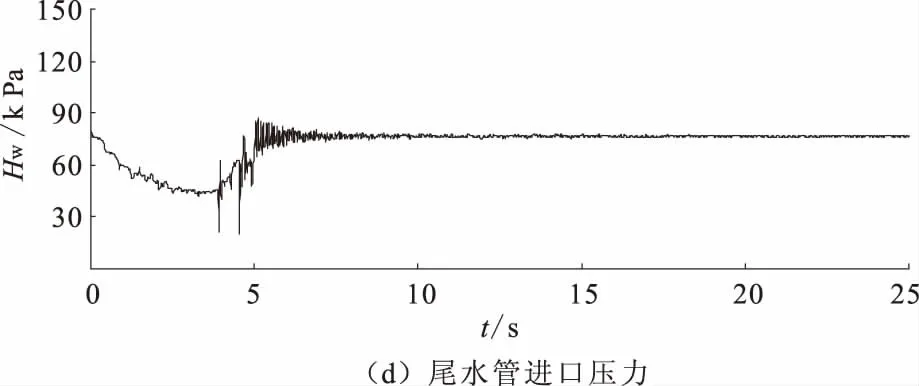
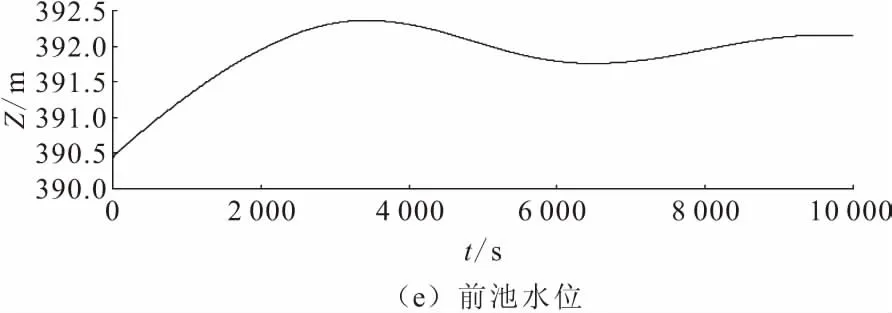
图4 工况T1Q主要参数的大波动过渡过程线
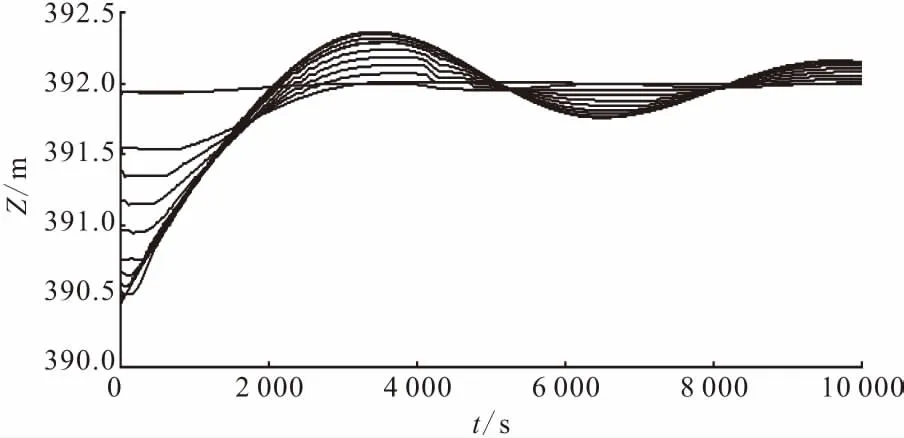
图5 工况T1Q对应的明渠沿线各断面水位变化过程线
曼维莱水电站大波动过渡过程计算分析表明:
(1)前池最高水位发生在T1Q工况,其值为392.362 m,低于相应的渠道末端顶高程394.27 m,有较大的裕度,满足布置要求;前池最低水位发生在T6工况,其值为390.015 m,略高于依据有压进水口临界淹没深度确定的允许最低水位389.58 m,满足布置要求。
(2)压力钢管上平段末端最小内水压力发生在T6工况,其值为2.25 m水柱,超过允许值2.0 m水柱,满足系统布置要求;压力钢管上平段末端顶部最大内水压力为163.4 kPa。
(3)机组蜗壳进口的最大内水压力发生在T5Q工况,其值为920.8 kPa,小于允许值982.5 kPa,有较大的裕度;机组蜗壳进口的最小内水压力值为404.9 kPa。
(4)尾水管进口最小内水压力发生T5工况,为-35.6 kPa,大于允许值-80 kPa,亦满足要求。
(5)机组最大转速出现在T5Q工况,其值为216.37 r/min,小于允许值216.71 r/min,相应最大转速上升率为29.80%,小于允许值30%,满足要求。
(6)结合前池水位的极值,以及压力钢管上平段末端和蜗壳进口内水压力的极值,可得到压力钢管沿线的最大/最小测压管水头线,见图6。
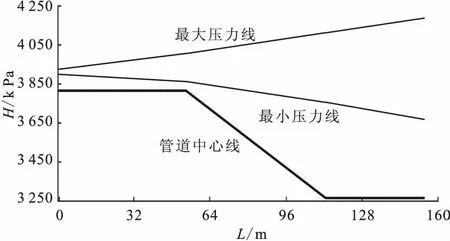
图6 压力钢管沿线的最大/最小测压管水头线
4 结 语
(1)大波动过渡过程模拟分析是水电站调保计算的重要手段,尤其是在电站设计阶段,过渡过程模拟可以为电站布置的合理性和电站运行的可靠性提供重要的参考和依据。
(2)曼维莱水电站大波动过渡过程计算表明,该电站引水发电系统建筑物布置安全合理,水库正常蓄水位条件下渠道均能满足引用流量要求;前池的最高水位低于二道坝坝顶高程及渠道末端顶部设计高程;前池的最低水位略高于依据有压进水口临界淹没深度确定的允许最低水位,建议实际运行时,前池的下限水位为390.0 m,当前池水位接近该下限水位时渠道已达到其最大过流能力,正常运行的机组应降低出力运行甚至停机,已避免前池水位进一步降低,不满足有压进水口的布置要求。压力钢管上平段末端顶部最小内水压力、机组蜗壳进口的最大内水压力、尾水管进口最小内水压力以及机组最大转速上升率均满足计算准则的要求。
(3)本工程前池利用一天然洼地布设而非人工前池,容积较大,调节能力较强。大波动过渡过程计算得出前池的最高涌浪水位为392.362 m,仅略高于前池的初始最高水位392.000 m,故本工程在布置上取消了前池溢流设施,极大地降低了前池设计和施工难度,具有显著的经济效益和参考价值。
(4)曼维莱水电站枢纽的输水系统主要由输水渠道、前池、压力管道、水轮机和尾水管等主要建筑物组成,其水力特性复杂,涉及渠道流的水面线和瞬变流计算分析,以及有压管流的瞬变流计算分析。本文针对具体电站做模拟分析,可以对同类型电站调保计算起到一定的参考作用,但是遇到其他电站,应该具体问题具体分析,切实保证电站的安全运行。
[1] 郑源,张健. 水力机组过渡过程[M]. 北京:北京大学出版社,2008.
[2] 杨建东. 导叶关闭规律的优化及对过渡过程的影响[J]. 水力发电学报,1999(2):75-82.
[3] 克里夫琴科. 水电站动力装置中的过渡过程[M]. 北京:水利出版社,1981.
TV131.4
A
1007-6980(2017)03-0027-04
刘国强 男 工程师 中水北方勘测设计研究有限责任公司 天津 300222
李永胜 男 工程师 中水北方勘测设计研究有限责任公司 天津 300222
郭 霄 男 工程师 中水北方勘测设计研究有限责任公司 天津 300222
徐 强 男 助理工程师 中水北方勘测设计研究有限责任公司 天津 300222
2017-07-05)
