叶片包角对离心泵流场及脉动特性的影响
2017-11-13,,2,,,
, ,2, , ,
(1.上海理工大学 能源与动力工程学院,上海 200093; 2.上海理工大学 上海市动力工程多相流动与传热重点实验室,上海 200093; 3.上海船舶设备研究所,上海 200031)
叶片包角对离心泵流场及脉动特性的影响
谢志宾1,陈二云1,2,丁京涛1,杨爱玲1,李国平3
(1.上海理工大学 能源与动力工程学院,上海200093;2.上海理工大学 上海市动力工程多相流动与传热重点实验室,上海200093;3.上海船舶设备研究所,上海200031)
针对离心泵非定常流动压力脉动特性,采用滑移网格的大涡模拟技术对叶片包角分别为95°,100°,105°,108°的4副叶轮进行数值模拟.分析了叶片包角对离心泵水力性能、叶轮出口“射流-尾迹”、测点压力脉动频谱特性和叶轮径向力的影响关系.结果表明:随着包角的增大,离心泵的水力性能下降;包角适当增大,会使叶轮射流-尾迹流动结构变弱.在设计工况下,蜗舌附近测点压力脉动最大;在蜗壳螺旋段压力脉动强度沿流动方向逐渐变弱,而在叶轮流道内压力脉动沿流动方向逐渐增强,在叶轮出口处达到最大;而离心泵叶轮所受径向力随着包角的增大而减小,适当地增大包角可以提高离心泵运行的可靠性.
叶片包角; 射流-尾迹; 压力脉动; 径向力
离心泵是一种将机械能转换成流体动能和压能的通用机械,在国民生产中占有重要地位[1].离心泵在运行过程中,由于非对称的蜗壳结构、叶轮的高速旋转及其内部流动的非定常激励力影响,使得离心泵内部产生周期性的压力脉动,这将引起振动和噪声,降低泵运行的可靠性.因此,离心泵内部的压力脉动特性引起了许多学者的高度关注[2-4].
叶片包角作为离心泵的重要设计参数之一,对离心泵的性能和压力脉动特性有十分重要的影响[5].过小的包角降低了叶片对流体的控制能力,不利于提高泵的效率;过大的包角增大了叶片摩擦损失,也不利于性能的提高.目前已有很多学者针对叶片包角对离心泵内部流动的影响进行了广泛的研究,杨华等[6]采用试验和数值模拟的方法对不同包角下的离心泵性能进行了试验和模拟对比,并分析了性能的差异.Yang等[7]采用试验和数值模拟的方法研究了叶片包角对离心泵的性能影响,通过对比发现,在不同范围内,包角大小的变化对离心泵的性能会有不同的影响:在相对小角度下,随着包角的增加,泵性能提升;而在相对大角度下,却出现相反的结论.张翔等[8]基于CFD数值计算方法分析了不同叶片包角与离心泵性能的关系,得出了离心泵扬程和功率特性发生变化的原因在于叶轮出口相对速度液流角发生改变.王勇等[9]采用试验的方法分析了不同叶片包角对离心泵空化振动流动诱导噪声的影响.
叶片包角问题引起了许多学者的高度关注,但是,大多数学者的研究只关注叶片包角的变化对离心泵整机性能的影响,而对叶片包角变化影响叶轮出口“射流-尾迹”及压力脉动的研究相对较少.作者通过数值求解方法,分析不同叶片包角对离心泵内部流动特征及压力脉动及叶轮径向力的影响,为离心泵叶轮叶片包角的设计提供一定的参考依据.
1 计算模型和数值模拟方法
1.1计算模型及网格
研究的原型泵型号为IS100-80-160单级单吸离心泵,泵的设计流量QS=100 m3/h,设计扬程H=32 m,转速n=2 900 r/min,模型的基本参数如表1所示.整个离心泵的计算域如图1所示.为了提高计算精度和收敛性,蜗壳和叶轮流体域全部用六面体网格生成,并且在叶片和蜗壳的壁面均进行边界层的加密,蜗壳壁面第一层网格尺度为0.012 mm,保证压力脉动分析的准确性[10].

表1 离心泵主要几何参数Tab.1 Main geometric parameters of the centrifugal pump

图1 离心泵计算域模型Fig.1 Computational domain of the centrifugal pump
1.2包角的选定
叶片包角是离心泵叶片的一个重要几何参数,其值的大小实质表征了叶片流道的扩散程度[11].叶片包角φ定义为叶片入口边与圆心的连线和出口边与圆心连线间的夹角[12],如图2所示(见下页).在对许多具有较好水利性能的叶轮进行研究的基础上,有学者给出了Zφ/360随着比转速ns变化的最优规律,如表2所示[13].原始离心泵模型的比转速为131.12,由此根据表2确定了模型泵叶片包角的取值范围为90~108 °,保证离心泵的主要基本参数不变,选用叶片包角依次为95,100,105,108 °这4副叶轮,通过数值求解的方法来研究包角变化对离心泵内部非定常流动压力脉动特性和叶轮径向力的影响,从而为离心泵的设计与优化提供参考.
1.3大涡模拟控制方程及边界条件

图2 叶片包角示意图Fig.2 Schematic diagram of the blade wrag angle

表2 叶片数Z与包角φ的乘积与比转速ns的关系
离心泵内部的流动是十分复杂的三维紊流流动,而大涡模拟能够捕捉到离心泵叶轮流道内复杂的湍流流动现象[14].大涡模拟是计算流体力学中的一种十分重要的数值模拟方法,它是基于一种数学滤波函数,通过在大涡流场中引入应力项来过滤掉小涡对大涡的影响,在流体机械非定常流动模拟计算中具有很大优势[15].本文以模型泵为基础,通过求解三维不可压非定常流动N-S方程获得离心泵内非定常流动的数值解,初始流场由离心泵流场的定常数值解近似给出,其控制方程为

(1)
(2)
式中:带上划线的量是滤波后的场变量;ρ为流体的密度;μ为流体的动力黏性系数;τij为亚格子尺度应力;t为时间;ui,uj为i,j方向上的雷诺时均速度.
2 计算结果分析
2.1外特性曲线分析
从流量-扬程功率曲线图3中可以看出,随着叶片包角的增大,离心泵的扬程H在相应流量下明显下降。Q/QS为流量比.轴功率P随着叶片包角的增大而减小,包角增大,相应流量下消耗的功率变小,叶片包角从95 °增加到108 °,设计工况下扬程下降了3.83%,轴功率下降了2.92%.

图3 流量-扬程曲线Fig.3 Lift against flow coefficient
从流量-效率曲线图4可以发现,在小流量情况下,随着叶片包角的增大,泵的效率η有升高的趋势,而在大流量下,离心泵的效率因包角的增大而显著下降.4副叶轮的最高效率在设计工况下分别为81.95%,81.84%,81.77%,81.19%,效率下降了0.76%.包角为95 °时,效率最高,这是因为叶片包角增大后,叶片变长,当量扩散角变小,叶片对流体的约束能力增强的同时摩擦损失也越来越大,从理论上来讲,必定存在最优的叶片包角.同时,随着叶片包角的增大,泵最高效率点的流量也相对减小,根据叶轮和蜗壳的耦合关系[16],叶片包角的增大使得叶片出口安放角和叶轮出口相对液流角减小,从而会引起泵最高效率点流量偏向小流量.由4副叶轮的性能计算结果可见,随着包角的增大,离心泵的扬程下降且效率减小.95 °叶片包角的性能要明显优于其他几副叶轮.在叶轮外尺寸确定后,造成这些性能差异的根本原因是包角变化引起叶片出口角、流道长度和叶型的改变,而不同的叶型使得叶轮内部的流场结构不同,包角的改变导致叶轮内部流动损失差异和叶片出口液体的滑移,最终使得叶片包角改变了离心泵的外特性.
2.2叶轮出口流动状态
为了研究包角的改变对叶轮出口流动状态的影响,图5给出了叶轮出口径向速度Cr沿周向的分布.其中:X=0,表示叶片压力面位置;X=1,表示叶片吸力面位置.叶轮出口20%叶高为靠盘侧,50%叶高为跨盘盖流道中央,80%叶高处为靠盖侧.U2为周向速度.可以看出,在叶轮出口处径向速度沿周向分布非常的不均匀,叶片的压力面侧存在着径向速度的高速区,而在叶片的吸力面侧则对应着径向速度的低速区.这实际上反映的就是叶轮出口的“射流-尾迹”流动结构;由于尾迹区实质上是低速流体微团的聚集区,其存在将导致流体在叶轮流道的出口处产生“堵塞”,减小有效通流面积,增加速度分布的不均匀性,影响叶轮出口流动状态.从图5中可以看出,靠盘侧叶轮出口径向速度随包角变化不明显,而从跨盘盖中央与靠盖侧整体上来看,在X=0.5处,径向速度“亏损”最大,径向速度随着包角的增大先呈现一定的平缓趋势而后波动变大.这说明过大或者过小的包角加强了叶轮出口射流-尾迹流动结构,使叶轮内部由边界层分离、漩涡二次流和尾迹等引起的涡流损失变大,而在一定范围内相对大叶片包角减弱了叶轮出口的射流-尾迹,使叶轮内部的涡流损失变小.

图4 流量-效率曲线Fig.4 Efficiency against flow coefficient
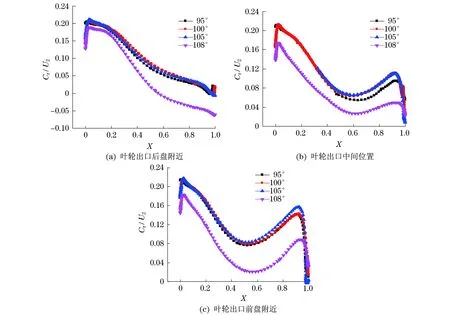
图5 不同包角下叶轮出口径向速度Cr沿周向分布Fig.5 Radial velocity along circumferential direction at different wrap angles
2.3压力脉动分析
由于流体的黏性作用及叶轮出口与蜗壳进口动静部件的相互干涉作用,使得离心泵内的流场呈现非定常流动特征,从而引起流场的压力脉动.这种周期性的压力脉动会引起系统及设备的振动和噪声,严重时会导致设备损坏.
为了监测离心泵在设计工况下内部压力脉动,引入了无量纲压力系数Cp=Δp/(0.5ρU2),其中,Δp为压力与平均压力的差值,ρ为水的密度.在离心泵蜗壳壁面的中截面上及沿叶轮流道中间位置设置了监测点y1,y2,y3,y4,y5和p1,p2,p3,p4,p5,如图6所示.
图7给出了不同包角下蜗壳螺旋段测点的压力脉动频谱特性,f为频率.从图7中可以看出,不同包角下的离心泵压力脉动信号均呈现出明显的离散特性,并且各测点压力脉动的主频均在叶频处.压力脉动最大的地方出现在蜗舌附近的p1点处,在此位置处的压力脉动低频信号也比较丰富.从p1点起,流体沿流动方向各测点在主频上的压力脉动强度逐渐减弱,高频成分逐渐消失.这是因为受到叶轮出口处的射流-尾迹作用及蜗壳断面几何形状影响,隔舌处径向间隙小,叶轮与蜗壳的动静干涉作用最强烈,沿着流动方向径间隙变大,动量掺混作用也就随之变弱.
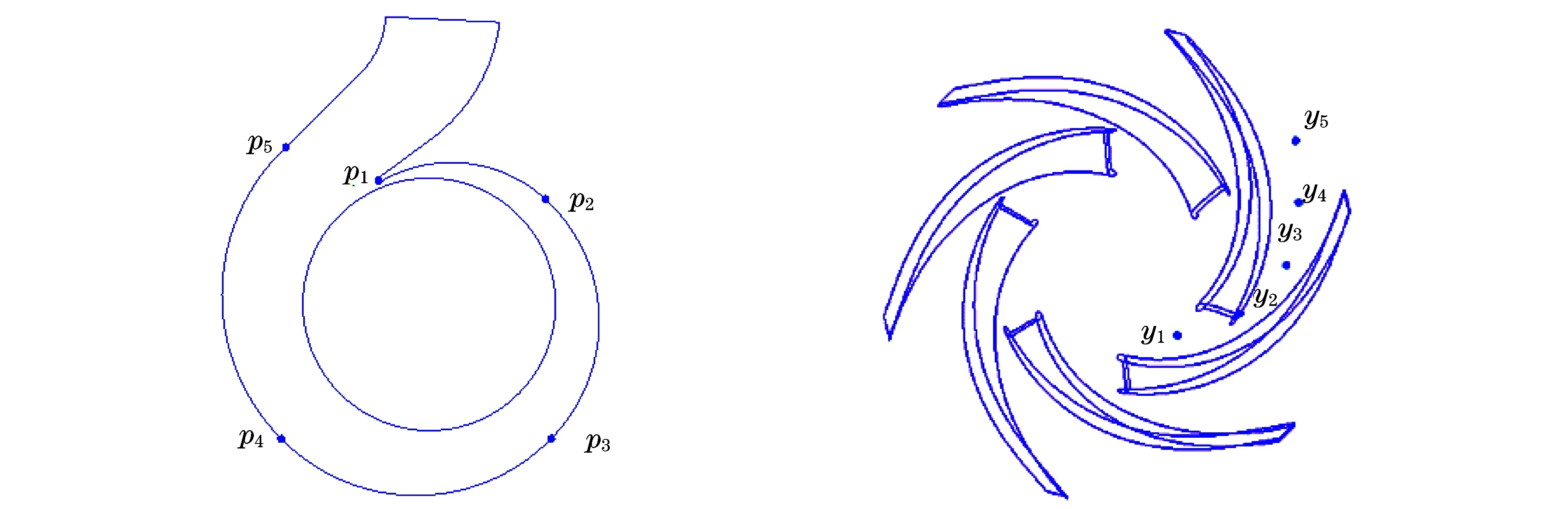
图6 监测点位置示意图Fig.6 Schematic diagram of monitoring points

图7 不同包角蜗壳螺旋段测点的压力脉动频谱图Fig.7 Frequency spectrum of the pressure pulsation in the spiral case with different wrap angles
蜗舌附近是离心泵内部距离叶轮最近的区域,也是叶轮通道气流流出直接冲击的部位,该部位最能体现压力的非定常变化,选择蜗舌处监测点p1进行研究.图8给出了不同包角下蜗舌处测点压力脉动频谱特性,从图8中可以看出,在p1处监测点压力脉动的低频特性十分复杂,并且不同叶片包角在叶频处压力脉动最为强烈,由于蜗舌的存在和叶轮出口气流的扰动作用使得蜗舌附近的流场较为复杂,表明了叶频脉动是压力脉动的主要贡献因素.而除了叶频外,在2倍叶频和3倍叶频处也存在脉动相对明显的峰值,随后幅值逐渐减小,这是因为在叶轮旋转过程中监测点受前一个叶片产生的压力脉动的影响还未消失时,后一个叶片又从该位置经过.

图8 不同包角蜗舌处测点压力脉动频谱图Fig.8 Frequency spectrum of the pressure pulsation at the measuring point on the volute tongue
同时,为了更加清楚地呈现不同包角对压力脉动强度的影响,对于p1点在叶频下的压力脉动强度用直方图表示,如图9所示.可以清晰地看出,随着包角的增大,压力脉动幅值先增大后减小,95 °包角时压力脉动最弱,105 °包角时压力脉动最强,叶片包角从95 °增加到105 °时,脉动幅值增加了14.7%.该现象与前面分析叶轮出口处射流-尾迹结构现象不一致,这可能是由于此时叶轮与蜗舌处的动静干涉作用强于射流-尾迹结构带来的压力脉动强度.
图10 (见下页)给出了设计工况下不同包角叶轮流道内测点的压力脉动频谱特性,可以发现,在叶轮流道内沿着流体流动方向,各测点的压力脉动幅值在叶频及谐频处均增大,位于叶轮进口处的测点y1的压力脉动最弱,而距离叶轮出口处最近测点y5的压力脉动则最为强烈.由此说明叶轮内压力脉动沿着流体流动的方向逐渐增强,在叶轮出口处压力脉动表现得最为强烈,这是因为叶轮流道的出口处射流-尾迹结构作用明显且距离蜗壳壁更近,动静耦合干扰作用造成出口处湍流十分强烈,从而导致脉动幅值很大.同时可以发现,随着包角的增大,叶轮出口y5压力脉动整体呈现递减,这与包角增大导致叶轮出口处射流-尾迹减弱的规律一致.
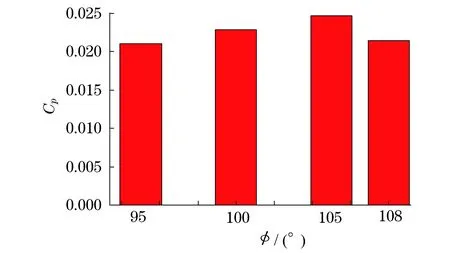
图9 不同包角蜗舌测点压力脉动强度直方图Fig.9 Frequency histogram of the pressure pulsation at the measuring point on the volute tongue
2.4叶轮径向力分析

从图11中可以看出,离心泵叶轮所受径向力呈现明显的周期性和脉动性,波峰和波谷的数目与叶片数呈现对应关系,并且随着叶片包角的增大,径向力幅值呈现减小趋势.图12 (见下页)为叶轮所受径向力的频谱分析,径向力呈现出明显的离散特性,不同包角下叶轮径向力最大幅值均出现在叶频处,同时在二阶和三阶叶频及谐频处都出现了较大谐波.为了能够更加清楚地呈现不同包角下径向力的变化情况,图13 (见下页)给出了叶频下不同包角的径向力大小直方图,可以清楚地看到,叶频下径向力的幅值随着包角的增大而逐渐减小.在叶频下叶片包角从95 °增加到108 °时,径向力下降了16.0%,由此可见,包角增大,增强了离心泵运行的可靠性.压力沿叶轮出口分布不均导致离心泵叶轮受到径向作用力,包角的改变对叶轮径向力的规律同对叶轮出口处射流-尾迹的规律一致,证明了之前包角对叶轮出口流场影响结论的准确性,也说明包角改变了叶轮出口的压力分布,从而影响了叶轮径向力的产生.

图10 不同包角叶轮流道内测点压力脉动频谱图Fig.10 Frequency spectrum of the pressure pulsation at the measuring point in the impeller with different wrap angles

图11 不同包角叶轮径向力差时域图Fig.11 Time-domain diagram of the radial force difference of the impeller with different wrap angles
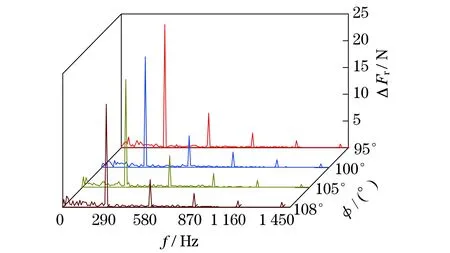
图12 不同包角叶轮径向力差大小频域图Fig.12 Frequency spectrum of the radial force difference of the impeller with different wrap angles
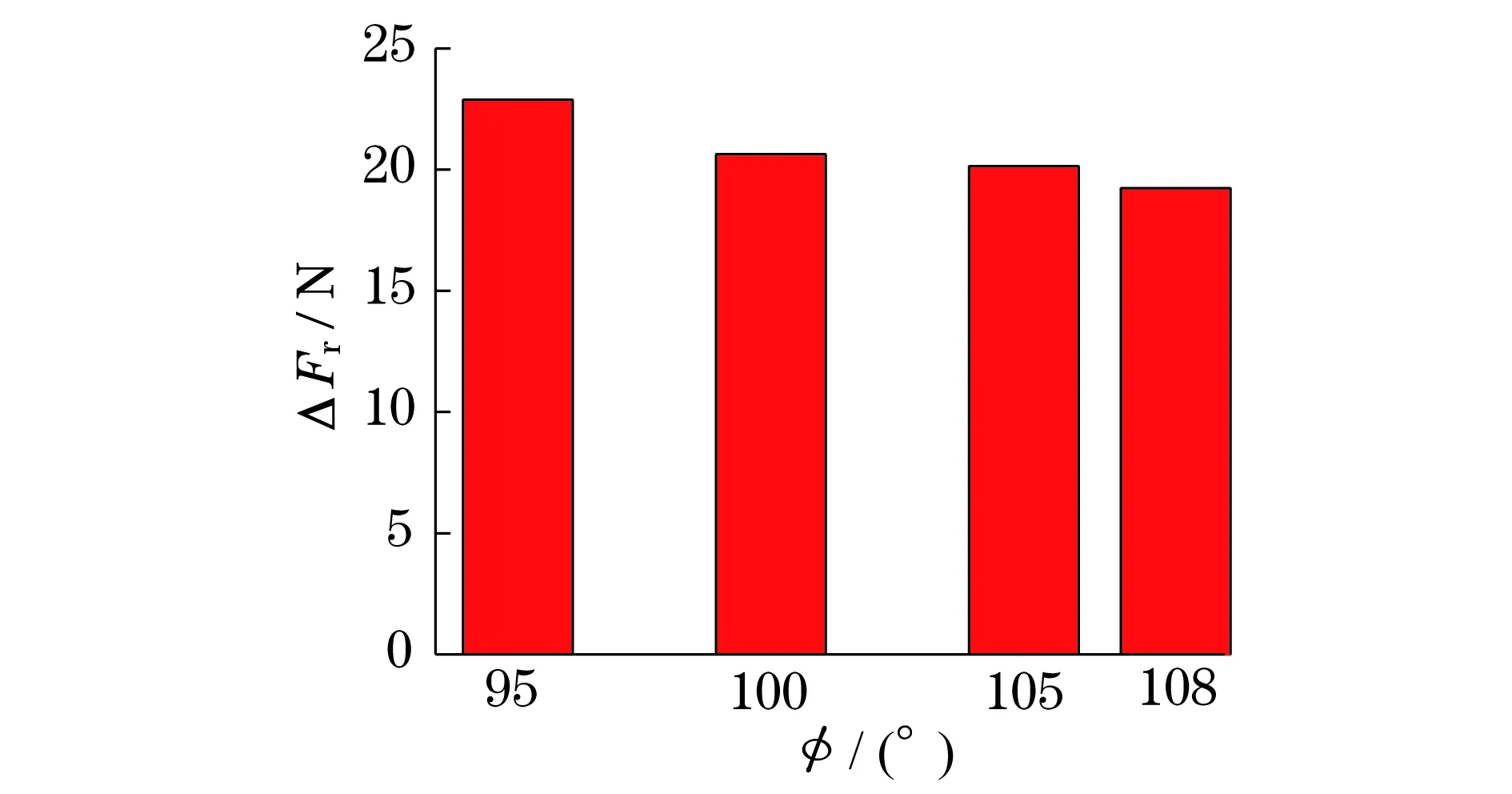
图13 不同包角径向力差大小直方图Fig.13 Frequency histogram of the radial force difference of the impeller with different wrap angles
3 结 论
a. 随着叶片包角的增大,叶轮出口相对液流角减小,进而改变了离心泵的外特性,具体表现为,随着叶片包角的增加,离心泵的扬程下降,离心泵的效率降低,且最大值向小流量方向偏移.
b. 包角的变化改变了叶轮流道的结构.从而使得叶轮内部的流场发生变化,产生了射流-尾迹结构,随着包角的增大,叶轮内部射-流尾迹作用先减弱后加强.
c. 蜗壳螺旋段测点沿流动方向,尾迹流的动量掺混作用随距离尾缘越远而越弱;沿叶轮流道流动方向,压力脉动逐渐增强,叶轮出口处压力脉动最为强烈;随着包角的增大,蜗舌处压力脉动强度先增大后减小,而叶轮出口处的压力脉动却先减小后增大,这是射流尾迹结构作用和叶轮与蜗壳动量掺混作用相互耦合导致的.
d. 叶轮所受径向力表现出明显的周期性,且径向力脉动频率在叶频处强度最大;径向力随着叶片包角的增大而减小,因此,适当地增大叶片包角,可以提高离心泵运行的可靠性.
[1] TAN L,CAO S L,GUI S B.Hydraulic design and pre-whirl regulation law of inlet guide vane for centrifugal pump[J].Science China Technological Sciences,2010,53(8):2142-2151.
[2] KAUPERT K A,STAUBLI T.The unsteady pressure field in a high specific speed centrifugal pump impeller-part I:influence of the volute[J].Journal of Fluids Engineering,1999,121(3):621-626.
[3] GUELICH J F,BOLLETER U.Pressure pulsations in centrifugal pumps[J].Journal of Vibration and Acoustics,1992,114(2):272-279.
[4] DONG R,CHU S,KATZ J.Effect of modification to tongue and impeller geometry on unsteady flow,pressure fluctuations,and noise in a centrifugal pump[J].Journal of Turbomachinery,1997,119(3):506-515.
[5] 张启华,李月仙,林建忠,等.基于纸浆泵流场数值模拟的叶轮设计准则及其应用[J].江苏大学学报(自然科学版),2011,32(2):185-189.
[6] 杨华,刘超,汤方平,等.不同叶片包角的离心泵试验与数值模拟[J].机械工程学报,2007,43(10):166-169.
[7] YANG S S,KONG F Y,CHEN H,et al.Effects of blade wrap angle influencing a pump as turbine[J].Journal of Fluids Engineering,2012,134(6):061102.
[8] 张翔,王洋,徐小敏,等.叶片包角对离心泵性能的影响[J].农业机械学报,2010,44(11):38-42.
[9] 王勇,刘厚林,刘东喜,等.叶片包角对离心泵流动诱导振动噪声的影响[J].农业工程学报,2013,29(1):72-77.
[10] 马尊领,郭艳丽,陈二云,等.离心泵压力脉动的数值模拟及敏感性分析[J].工程热物理学报,2015,36(7):1461-1465.
[11] 严敬,张江源,何敏,等.离心泵可控包角圆柱形叶片型线方程[J].排灌机械,2008,26(5):46-49.
[12] 离心泵设计基础编写组.离心泵设计基础[M].北京:机械工业出版社,1974:134-162.
[13] 陈乃祥,吴玉林.离心泵[M].北京:机械工业出版社,2003:105-117.
[14] BYSKOV R K,JACOBSEN C B,PEDERSEN N.Flow in a centrifugal pump impeller at design and off-design conditions-Part II:large eddy simulations[J].Journal of Fluids Engineering,2003,125(1):73-83.
[15] 王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004:15-35.
[16] 张翔.低比速离心泵蜗壳对水力性能的影响[D].镇江:江苏大学,2008.
EffectofBladeWrapAngleontheInternalFlowFieldandPressurePulsationinCentrifugalPumps
XIE Zhibin1,CHENEryun1,2,DINGJingtao1,YANGAiling1,LIGuoping3
(1.SchoolofEnergyandPowerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China; 2.ShanghaiKeyLaboratroyofMultiphaseFlowandHeatTransferinPowerEngineer,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China; 3.ShanghaiMarineEquipmentResearchInstitute,Shanghai200031,China)
For investigating the pressure pulsation characteristics of the unsteady flow in centrifugal pumps,a single-stage single-suction centrifugal pump was taken as an example to perform a numerical simulation by using the technology of large eddy simulation with sliding grid.The three dimensional flow field was simulated numerically with the blade wrap angle 95 °,100 °,105° and 108° respectively.The influences of the blade wrap angle on the centrifugal pump hydraulic performance,impeller exit jet-wake,pressure pulsation frequency spectrum characteristics at each measuring point and radial force of the impeller were analyzed.The results show that as the angle increases,the centrifugal pump hydraulic performance degradates.The angle increase will lead to the impeller outlet jet-wake flow structure.Under design conditions,near the volute tongue the pressure pulsation at measuring points is the strongest,at the spiral screw section along the flow direction,the pressure pulsation intensity gradually weaken,and at the impeller passage point along the flow direction,the pressure pulsation gradually enhances and reaches the maximum at the impeller outlet.The radial force of the centrifugal pump impeller decreases with the increase of angle.Therefore,appropriately increasing the wrap angle can improve the reliability of the centrifugal pump running.
bladewrapangle;jet-wake;pressurepulsation;radialforce
1007-6735(2017)05-0430-08
10.13255/j.cnki.jusst.2017.05.005
2017-03-14
国家自然科学基金资助项目(51106099,50976072);上海市科委科研计划项目(13DZ2260900)
谢志宾(1990-),男,硕士研究生.研究方向:叶轮机械气动力学.E-mail:xiezhibin2015@163.com
陈二云(1977-),男,副教授.研究方向:叶轮机械气动力学和声学.E-mail:cheneryun@usst.edu.cn
TH311
A
(编辑:石 瑛)
