二维弹簧振子在匀强磁场中运动规律的研究

涂德新 姜付锦

(1.江西师范大学附属中学,江西 南昌 330046; 2. 武汉市黄陂区第一中学,湖北 武汉 430300)

二维弹簧振子在匀强磁场中运动规律的研究

涂德新1姜付锦2

(1.江西师范大学附属中学,江西 南昌 330046; 2. 武汉市黄陂区第一中学,湖北 武汉 430300)

本文首先推导了二维弹簧振子在匀强磁场中运动的参数方程,接着求出了小球的极值位置,并求出了小球进动的角速度,得到了轨迹闭合的条件，最后进行了数值模拟．

参数方程;进动角速度;闭合条件;数值模拟

1 提出问题

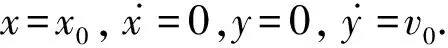
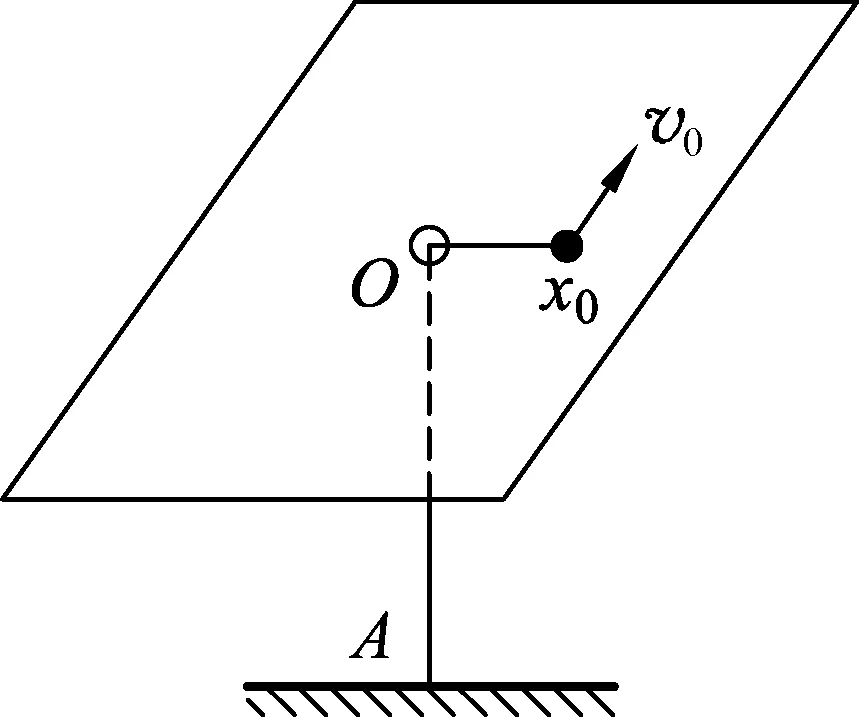
图1

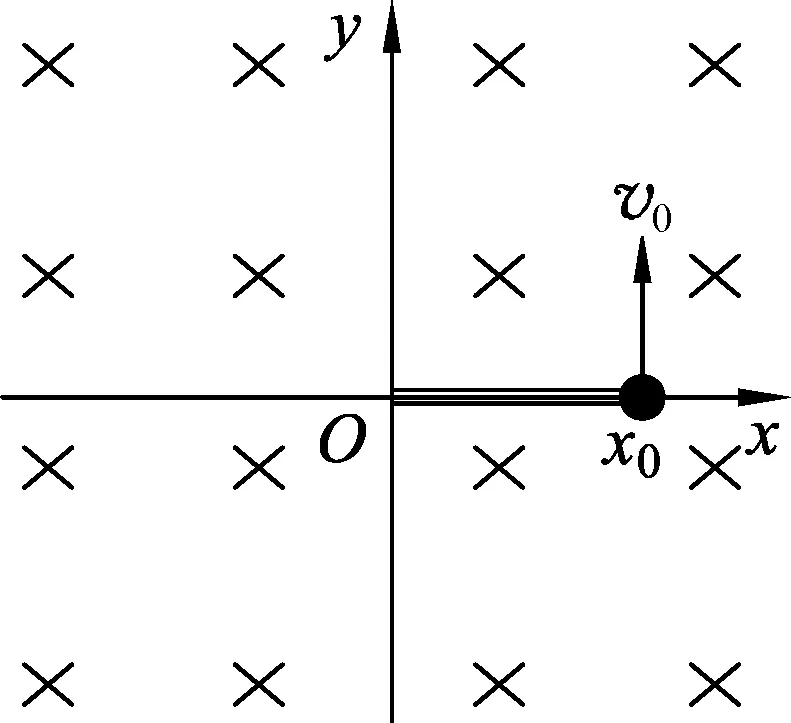
图2

1.1 弹簧振子运动的微分方程

对小球应用牛顿第二定律有

写成分量式为

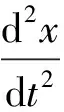
(1)

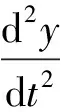
(2)

1.2 复数法求微分方程的通解

设z=x+yi，则(1)、(2)式可以改写为

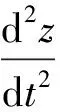
(3)

特征根方程为

特征根为

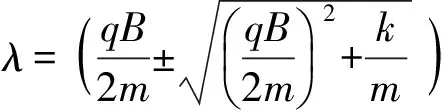
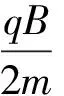
z=z1eλ1t+z2eλ2t.

其系数z1z2应该为复数,可以写为

z=(C1+C2i)eαti+(C3+C4i)eβ ti.

展开得

z=(C1cosαt-C2sinαt+C3cosβt-C4sinβt)+(C1sinαt+C2cosαt+C3sinβt+C4cosβt)i.

于是可得

x=C1cosαt-C2sinαt+C3cosβt-C4sinβt.

(4)

y=C1sinαt+C2cosαt+C3sinβt+C4cosβt.

(5)

其中C1,C2,C3,C4为待定系数.

1.3 弹簧振子运动的参数方程

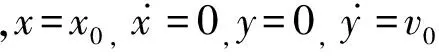
C1+C3=0,C2+C4=0,-C2α-C4β=0,C1α+C3β=0.

可以解得

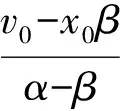
于是小球运动的参数方程为

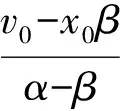
(6)

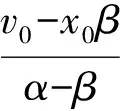
(7)

2 小球离原点的最值距离

由(6)、(7)式可得

(α-β)2r2=[(v0-x0β)cosαt+(x0α-v0)cosβt]2+[(v0-x0β)sinαt+(x0α-v0)sinβt]2.

化简得

(α-β)2r2=(v0-x0β)2+(v0-x0α)2-

2(v0-x0β)(v0-x0α)cos(α-β)t.

当t=0时，有

(α-β)2r2=[(v0-x0β)-(x0α-v0)]2=

(α-β)2x02，即rm1=x0.

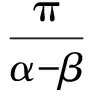
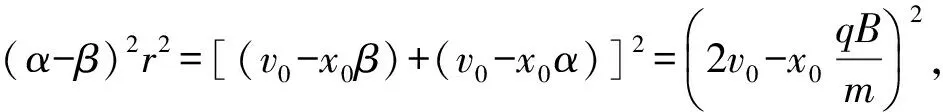
3 小球的进动角速度

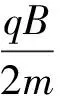
考虑到近似条件,y可以写为

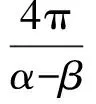
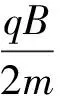
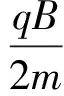
4 小球运动轨迹的闭合条件

可以发现如果α、β的比值为整数之比,即

5 数值模拟

为了数值模拟的方便,不妨设q=1,m=1,x0=3,g=10,图3给出了k、B、v0为不同值时的小球运动的轨迹图像．

k=3/4,B=1,v0=2

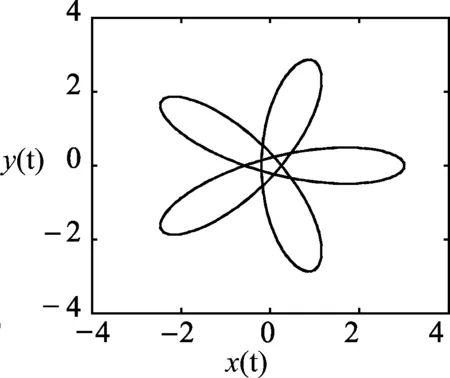
k=6,B=1,v0=2

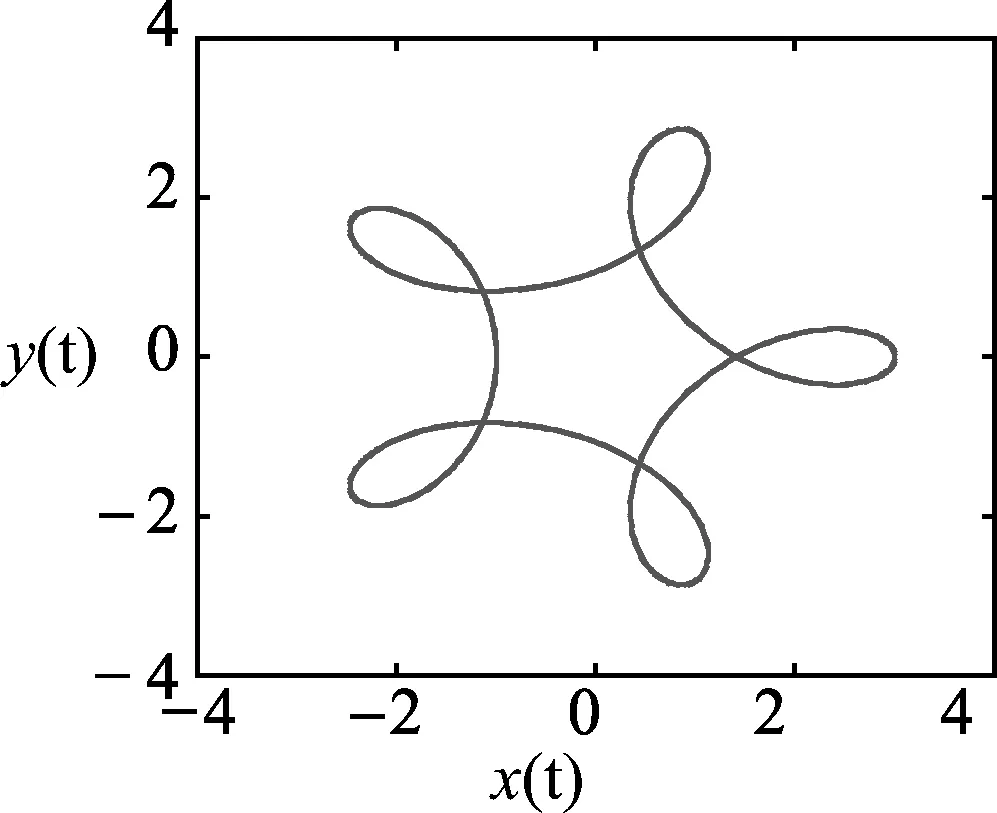
k=4,B=3,v0=2

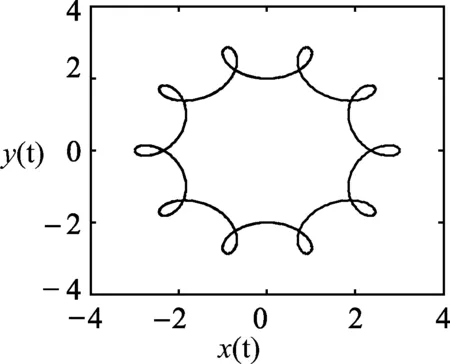
k=9/4,B=4,v0=2

6 小结

通过以上的分析不难发现, 小球运动的微分方程组是比较难求解的,本文通过复数法来处理,过程比较简洁,得到了小球运动的解析解．在磁感应强度比较小时,可以求出小球轨迹进动的角速度．如果满足一定的条件,则小球的轨迹是闭合的．同时由于洛伦兹力的存在使得x和y方向的运动会相互影响．

1 程稼夫.中学奥林匹克竞赛物理教程力学篇[M].合肥:中国科学技术大学出版社,2002:334.

2 陈钢. 用直角坐标方法分析带电粒子在复合场中的运动[J]. 物理教师,2016(02):85-86.

3 李海胜. 重力场和匀强磁场中的简谐运动问题解析[J]. 物理之友,2016(11):43，45.

2017-05-12)