深沟球轴承运转过程显式动力学数值仿真研究
2017-11-13陈曙光张洪伟蔡晓君
陈曙光 张洪伟 蔡晓君
(北京石油化工学院机械工程学院)
深沟球轴承运转过程显式动力学数值仿真研究
陈曙光 张洪伟 蔡晓君
(北京石油化工学院机械工程学院)
基于显式动力学有限元理论,应用ANSYS/LS-DYNA软件建立了6014深沟球轴承的多体接触力学模型。考虑转速和径向载荷的作用,在一定工况条件下进行了动力学仿真研究,分析了轴承运转过程中动态响应与接触应力的变化规律。结果表明:仿真结果与理论计算结果相吻合。
深沟球轴承 显式动力学 接触碰撞 有限元模型
滚动轴承是传递运动和承受载荷的重要支撑转动部件[1,2]。随着旋转机械朝着高转速、高稳定性、低噪声和低振动的方向发展,滚动轴承的动态性能问题日益突出[3~5]。因此,对轴承进行动力学分析,掌握其接触应力分布规律具有重要意义。
滚动轴承的力学模型经历了4个发展过程:静力学分析、拟静力学分析、拟动力学分析和动力学分析[5]。近年来,有限元方法、接触算法等的不断发展,促进了滚动轴承三维数值仿真的发展[6~11]。Stone B J利用计算机仿真模拟分析了球轴承中钢球运动与摩擦特性的关系,结果表明,轴承工作时由于滚动体滚动而产生的离心力对轴承疲劳寿命会产生很大影响,限制了轴承最高转速[6]。Wang J等采用全数值分析法,分别在纯滚动、滑移-滚动、纯滑动3种条件下进行了研究[7]。文献[8,11]利用ANSYS/LS-DYNA对滚动轴承的运动过程进行了仿真分析。唐云冰等利用ANSYS研究了滚动轴承的载荷分布[10]。SKF、NSK及FAG等公司逐步采用有限元仿真软件对滚动轴承的应力分布、多场耦合特性进行仿真计算,用于指导滚动轴承的设计、制造等,以提高轴承性能。
由于滚动轴承接触区域的位置、大小、形状及摩擦力分布等在分析前未知,而且会随着外载荷的变化而改变,因此轴承接触的动力学分析至关重要[11]。笔者以显式动力学为基础,以深沟球轴承6014为例,应用ANSYS/LS-DYNA建立了深沟球三维有限元模型,对轴承在一定速度和载荷下的运转过程进行了动力学分析,为滚动轴承的工程设计与仿真提供一定参考。
1 显式动力学分析的基本理论
LS-DYNA中显式动力学分析采用中心差分方法。将位移函数按泰勒级数展开,得到前后差分公式为:
(1)
(2)


(3)
(4)
轴承系统的动力学求解方程为:
(5)
其中,M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;Qt为节点载荷向量。
将式(3)、(4)代入式(5),得递推公式为:
(6)
其中:
(7)
(8)
中心差分法中,只有在时间步长比临界时间步长小的情况下,显式分析求解才是稳定的,即:

(9)
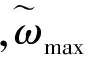
2 滚动轴承有限元模型的建立
2.1 滚动轴承结构尺寸
滚动轴承的结构参数如下[12]:
轴承外径D110mm
轴承内径d70mm
轴承宽度B20mm
内圈外径d282mm
滚球数目 13个
球径Dw13mm
外圈内径D298mm
笔者对建模过程进行了适当简化,如轴承的倒角和边棱对内部应力影响很小,可以忽略不计。在ANSYS中完成深沟球轴承三维模型的建立。
2.2 单元类型与网格划分
选用SOLID164单元进行网格划分,滚动体和内外圈采用六面体单元,保持架由于其结构不规则,采用四面体划分。由于SOLID164单元不具有旋转自由度,为了模拟轴承转动效应,将轴承内圈内表面设定为刚性面,利用SHELL163单元进行划分,以便施加转速和载荷。轴承有限元网格划分如图1所示,共75 282个节点,91 074个单元。

图1 轴承有限元网格划分
2.3 材料模型
由于笔者关注的是滚动体和内外圈的受力与变形情况,因此将保持架定义为刚体,计算过程中,刚体内的所有节点的自由度都耦合到其质心上,仅有6个自由度,可以提高计算效率。将滚动体和内外圈定义为弹塑性体,其中内外圈和滚动体的材料均用GCr15钢,保持架为冷轧钢板,材料参数为:密度ρ=7830kg/m3,弹性模量E=206GPa,泊松比v=0.3。
2.4 接触控制与边界条件
根据实际轴承工作环境,外圈与轴承座紧固,将轴承外圈固定,约束所有自由度,内圈施加径向载荷和转速。由于在有保持架的轴承中,滚动体与保持架的短期碰撞会使两者保持高度动态相互作用,为避免瞬时加速带来的影响,将转速在0~5ms内匀速加载。
接触设置是处理轴承接触关系的关键。由于运动过程中接触区域具有不确定性,因此,采用自动面面接触类型。将滚动体与内外圈和保持架分别建立接触对,假定静摩擦系数分别为0.35、0.35和0.20,动摩擦系数分别为0.16、0.16和0.10[8,11]。
3 轴承动力接触仿真分析
3.1 轴承运转过程动态响应分析
在深沟球轴承运转时,假定径向载荷Fr=2kN,转速为3 850r/min,分析该情况下的动态响应。
根据理论分析,假设沟道接触处没有严重打滑,则保持架的线速度vm是内圈沟道线速度vi和外圈沟道线速度vo的平均值,滚动体的公转速度与保持架一致[1]:

(10)
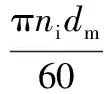

(11)
其中,ni为内圈转速;dm为节圆直径;γ为无量纲系数,γ=Dcosa/dm,Dw为球直径,a为接触角;no为外圈转速。
当外圈固定、内圈有转速时,保持架转速nm为:

(12)
对于滚动体,除了公转之外还有自转。假定内圈沟道和球接触处没有严重滑动,接触点上球的线速度与沟道线速度相同,所以:
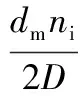
(13)
分别选择轴承滚动体、内圈和保持架上的某一节点,绘制沿x方向的位移曲线如图2所示,其中A为滚动体,节点号11 189;B为内圈,节点号5 673;C为保持架,节点号71 968。可以看出,内圈、保持架和滚动体的节点运动都具有周期性的变化规律,内圈做匀速转动,滚动体公转的同时自身还有自转,位移曲线的波峰表示与滚动体外圈接触的位置。内圈节点位移曲线的一个公转周期约15.58ms。保持架节点的位移公转周期为36.80ms。滚动体节点的位移公转周期为36.20ms,其自转周期为4.30ms。由式(9)~(13)可以计算得出,保持架的理论周期为36.30ms,滚动体自转的周期为4.34ms。仿真结果和理论结果是相吻合的。由于保持架存在兜孔间隙,轴承运转过程中会出现滚动体和保持架打滑的现象,导致滚动体和保持架旋转周期并不完全相同,这会导致两者之间发生接触碰撞。
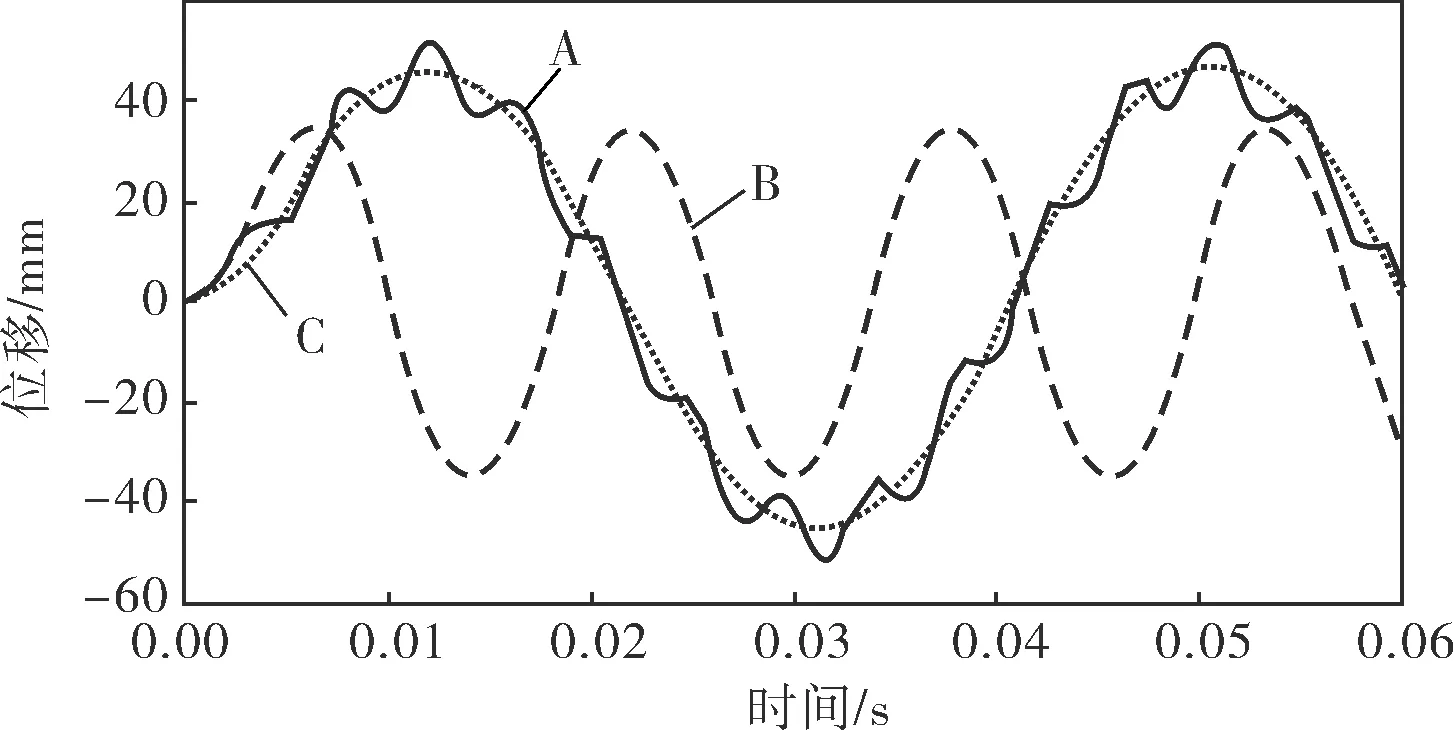
图2 滚动体、内圈、保持架上某一节点的位移曲线
图3为滚动体、内圈、保持架节点的速度曲线。可以看出,内圈在0.005s内做加速运动,保持架随着内圈的加速而加速,在加速过程中,曲线有波动现象,这是由保持架和滚动体的碰撞所导致。加速完成后,保持架和内圈的速度并不是保持不变,而是有微弱变化,这表明即使轴承在正常运转情况下,也是有振动的。滚动体节点的速度呈现出强烈的变化性,这和图2中滚动体节点位移曲线的周期性保持一致。

图3 滚动体、内圈、保持架上某一节点的速度曲线
图4(D为外圈,节点号3 993)反映了轴承各部分的速度变化有较强的非线性。由于轴承在运转过程中具有非线性变形,不可避免地会发生振动现象。滚动体的振动最为剧烈,内圈振动较小,保持架次之,外圈振动最小。

图4 滚动体、内圈、保持架上某一
3.2 轴承的动态应力分布规律
图5为轴承在不同时刻的等效应力云图。滚动体的最大应力出现在滚动体与内外圈的接触区域。滚动体受力位置和应力最大值在轴承运转过程中会发生变化。

a. t=10.2ms

b. t=20.4ms
图6为滚动体节点7 552的等效应力曲线。可以看出,由于滚动体在运转过程中与保持架会有碰撞现象发生,导致滚动体应力波动变化。突然变化的曲线表示单元进入与内外圈接触的区域。

图6 滚动体节点7 552的等效应力曲线
图7为滚动体节点7 552在不同转速下的等效应力曲线,与图6对比可以发现,在一定范围内,转速的增加会使滚动体最大应力峰值出现的时间提前,但不会使滚动体单元的最大应力值发生显著变化。

a. 4 500r/min
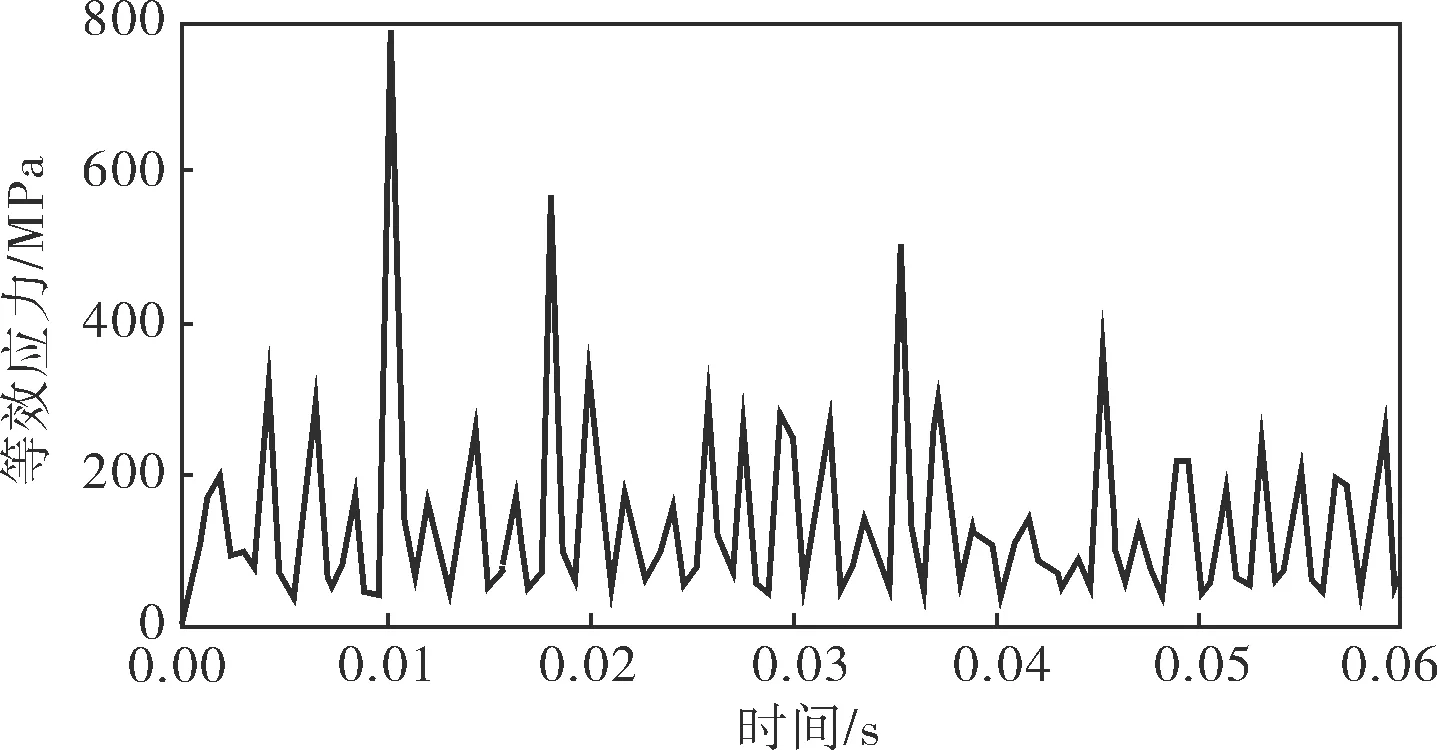
b. 5 800r/min
4 结论
4.1 基于显式动力学,建立了深沟球轴承有限元力学模型,在转速和径向载荷作用下进行了动力学分析。结果表明:滚动体的运动呈周期性变化规律,在每个周期内,滚动体与内外圈的接触位置有所变化。由于滚动体和保持架旋转周期并不完全相同,这会引起两者之间的接触碰撞。
4.2 轴承在运转过程中,速度、加速度曲线具有强烈的非线性,不可避免地会发生振动,其中滚动体的振动最为剧烈,内圈、保持架次之,外圈振动最小。
4.3 滚动体的最大应力出现在滚动体与内外圈的接触区域,轴承运转过程中,滚动体受力位置发生变化,应力最大值也随之发生变化。
4.4 在一定转速范围内,转速提高会使滚动体最大应力峰值出现的时间提前,但并不会使滚动体单元的最大应力值发生显著变化。
[1] Harris T A,Kotzalas M N,著,罗继伟,译.滚动轴承分析第2卷:轴承技术的高等概念[M].北京:机械工业出版社,2015:1~10.
[2] 王晓升,屈梁生,赵勃,等.轴承稳定性对悬臂式烟气轮机振动影响的研究[J].化工机械,1997,24(5):45~49.
[3] 曹莹,段玉波,刘继承.基于多尺度的形态滤波降噪方法[J].化工自动化及仪表,2015,42(11):1202~1205.
[4] Lundberg G,Palmgren A.Dynamic Capacity of Rolling Bearings[J].ActaPolytechnica Mechanical Engineering Series,1952,2(4):96~127.
[5] 吴云鹏,张文平,孙立红.滚动轴承力学模型的研究及其发展趋势[J].轴承,2004,(7):44~46.
[6] Stone B J.The State of the Art in the Measurement of the Stiffness and Damping of Rolling Element Bearings[J]. CIRP Annals-Manufacturing Technology,1982,31(2):529~538.
[7] Wang J,Kaneta M,Yang P.Numerical Analysis of TEHL Line Contact Problem under Reciprocating Motion[J].Tribology International,2005,38(2):165~178.
[8] 樊莉,谭南林,沈栋平.基于显式动力学的滚动轴承接触应力有限元分析[J].北京交通大学学报,2006,30(4):109~112.
[9] 刘旺玉,李静.基于Hertz理论的深沟球轴承动态接触分析[J].机械设计与制造,2011,(8):224~226.
[10] 唐云冰,高德平,罗贵火.航空发动机高速滚珠轴承力学特性分析与研究[J].航空动力学报,2006,21(2):354~360.
[11] 林腾蛟,荣崎,李润方,等.深沟球轴承运转过程动态特性有限元分析[J].振动与冲击,2009,28(1):118~122.
[12] Hallquist J O.LS-dyna Keyword User’s Manual Version 970[M].California:Livermore Software Technology Corporation, 2003:818.
MotionProcessNumericalSimulationforDeep-grooveBallBearingsBasedonExplicitDynamics
CHEN Shu-guang, ZHANG Hong-wei, CAI Xiao-jun
(CollegeofMechanicalEngineering,BeijingInstituteofPetrochemicalTechnology)
Basing on explicit dynamics theory and having ANSYS/LS-DYNA adopted, the multi-body contact mechanic model of a 6014 deep-groove ball bearing was established; considering the effects of the speed and load conditions, the dynamic response and contact stress variation of the bearings in motion were analyzed to show that, the simulation result coincides with the result theoretically calculated.
deep-groove ball bearing, explicit dynamics, multi-body contact, finite element model
北京石油化工学院优秀人才培育计划项目(14031821003-37);北京石油化工学院科技创新资助项目(15031862005/047)。
陈曙光(1991-),硕士研究生,从事机械产品现代设计和制造技术的研究。
联系人张洪伟(1978-),讲师,从事数字化设计与仿真、先进制造技术、机械系统动力学的研究,zhanghw@bipt.edu.cn。
TQ055
A
0254-6094(2017)02-0208-05
2016-02-29,
2016-05-23)
