基于速度矩守恒的离心泵节能蜗壳断面几何参数求解

严 敬，胡赞熬，刘小兵，周绪成



基于速度矩守恒的离心泵节能蜗壳断面几何参数求解

严 敬1,2，胡赞熬1,2，刘小兵1,2，周绪成3

（1. 流体及动力机械教育部重点实验室（西华大学），成都610039；2. 西华大学能源与动力工程学院，成都610039； 3. 成都市永益泵业有限公司，成都610300）

螺旋形蜗壳是离心泵的基本压水室形式，降低蜗壳中的流动损失是提高泵效率的重要措施。分析表明，蜗壳各轴面断面的周长是决定蜗壳中水力损失的重要因素。在传统的蜗壳设计方法中，并未重视蜗壳湿周与蜗壳水力损失的关系，也未将改善蜗壳断面几何特征作为产生节能产品的设计目标。该文以速度矩守恒原理为依据，在保证蜗壳断面入口无显著扩散的条件下，提出了实现蜗壳断面最小湿周的理念与实现方法。利用等面积图形中圆具有最小周长的几何特征，该文给出了与现行蜗壳断面有区别的断面确定原则，并根据断面要求通过的不同流量形成了2种减小断面湿周的断面新结构。由于这种断面几何参数没有解析解，该文给出了它们详尽的数值求解方法与过程。事实证明,该文提出的方法对改善泵效率有积极效果，在设计点附近的提高幅度均达到1.6%。该文设计的断面蜗壳有望成为实现改善泵效率这一预期目标的可行结构。

离心泵；设计；蜗壳；几何参数；数值求解

0 引 言

螺旋形蜗壳是离心泵的基本压水室形式。来自叶轮的水流在蜗壳的后续流动中不可避免地存在水力损失，其值可达到泵内全部水力损失的一半[1-3]。在保证蜗壳实现其基本功能的同时，力求将蜗壳中的流动损失降低到最低值无疑是提高离心泵效率、产生新型节能产品的重要措施。

螺旋形蜗壳的主体为一布置在叶轮周围且断面面积不断增大的螺旋管新型。在蜗壳的设计实践中，实际只需要正确确定8个夹角一定的螺旋管轴面断面的几何形态，这8个断面不仅决定了蜗壳的基本几何特征，也基本决定了蜗壳的水力性能。

国内外的水泵技术人员经过长时期的探索，已在蜗壳正反问题的研究中发表了较多成果。Lobanoff等在对大量优秀离心泵产品几何尺寸分析统计的基础上提出了在西方有影响的蜗壳各断面面积计算的经验公式，并提出了蜗壳断面形态标准化的理念[4-5]；Johann阐述了基于速度矩守恒原则的传统梯形断面几何参数的数值积分方法与过程[6]；Hamed等分析了蜗壳隔舌位置对泵外特性的影响[7]；高江永等通过系统分析叶轮与蜗壳几何参数的关系，提出了减小蜗壳中水力损失的优化目标[8]；严敬等曾将速度矩守恒原则应用于蜗壳修圆矩形断面与传统梯形断面的参数求解，提出了蜗壳8个断面的数值求解的原理及步骤[9-11]。以上列举的研究成果都在一定程度上提升了离心泵蜗壳设计水平，改善了产品的水力性能。

蜗壳轴面断面的求解长期使用2种经典方法：速度系数法和速度矩守恒方法。应指出，2种方法的应用与改进并未改变蜗壳断面的基本几何形态，即应用于低比转速泵的矩形断面与应用于中高比转速泵的梯形断面。这2种断面几何参数的形态的确定都有自身的理论与经验依据，但也存在一长期以来重视不足的问题:它们都未将蜗壳流动中的摩擦损失最小化作为突出目标，不含有尽量减小这种损失的主观意图。

本文将以速度矩守恒原理为基础，以减小蜗壳中流动损失为求解方向，提出与传统蜗壳断面有较大差别的断面几何形态及其求解方法。为此，先考查管流中水力损失的影响要素。

1 理论基础

在非圆断面的等截面直管中，水流的沿程损失h(m)以广泛使用的Darcy公式计算[12-14]。

式中为管长，m；为管道截面面积，m2；为截面湿周，m；为管中平均速度，m/s；为管中流量，m3/s；为无量纲系数；为重力加速度，m/s2。

离心泵的螺旋管并非等截面直管，但两者中的流动损失有相同的起因与机理，因而式（1）也定性适合离心泵螺旋管中的水力损失分析。

离心泵过流部件中的流动都在大雷诺数的湍流水力粗糙区[15-16]。式（1）中仅与管壁相对粗糙度有关而独立于流动雷诺数[17-18]，分析中可视为一常数。在，及也是常数的条件下，式（1）表明，管道中的水力损失将正比于管道断面湿周，湿周长成为决定管道水力损失的决定因素。这一结论也可从分析反映水力损失与管道雷诺数关系的Moody图得出。上述事实在过去研究中常被忽视，本文将在保证蜗壳实现其基本功能的条件下，以减小蜗壳断面湿周作为提高蜗壳效率的主要手段。

本文中提出的蜗壳断面的几何特殊性决定了断面几何参数没有解析解，本文将以数值计算方法，通过逐次逼近获得各断面控制参数。

2 基于速度矩守恒原则的极小湿周蜗壳断面设计

尽管在面积一定时，所有平面图形中圆具有最小周长，但离心泵蜗壳断面不宜使用圆形。这是因为水流从叶轮进入蜗壳后，由于流线不能突然转折，有可能在蜗壳下部生成2个漩涡脱流区。本文中，轴面上蜗壳断面下部仍使用两对称直线形成无转折的顺畅边璧。与传统的梯形断面不同处在于，本文以一条与两直线相切的圆弧代替传统的修圆梯形结构，其周长将比传统结构明显减小。这种断面形式的下部的两直线型腰避免了水流在蜗壳入口脱流，上部单圆弧形成的弓形减小了断面湿周，降低了水流沿程摩擦损失。本文中8个蜗壳断面的大多数将使用这种新型结构，新型蜗壳断面如图1所示。本文将以理论严格、已为设计实践证实可靠的速度矩守恒原理完成蜗壳各断面的设计计算。

注：b3为蜗壳进口各断面共同的宽度，m；R3为蜗壳基圆半径，m；γ为蜗壳下部直线型腰与铅垂方向夹角，(º)。

蜗壳断面设计的第一步应确定相关设计常量。在设计工况点，蜗壳中水流的速度矩2在其守恒条件下应等于叶轮出口速度矩2V2。由叶轮基本方程可以导出这一速度矩2V2=/(ηω)，这里和是给定的叶轮在设计点的扬程和叶轮旋转角速度，η是在叶轮设计阶段确定的叶轮水力效率。它们在后续计算中都是常数[19-20]。

按一般原则确定蜗壳进口各断面共同的宽度3，蜗壳基圆半径3及蜗壳下部直线型腰与铅垂方向夹角。为提高蜗壳的工艺性，8个断面上角应取同一值[21-23]。还应注意，较大的角有利于减小蜗壳径向尺寸，但会增加蜗壳入口脱流风险。

根据给定的设计流量(m3/s)，及8个断面在蜗壳中的位置，确定它们各自应通过的设计流量q，比如，对蜗旋线起于基圆的360°的蜗壳，显然有：

2.1 大流量断面几何参数的数值求解

在断面3，角给定条件下，确定该断面几何形状的核心步骤就是要确定上部单圆弧圆心到下部梯形下底的距离，如图2中。这是因为，一旦确定了值，图形的全部相关几何尺寸都可以由表示。

图2 新型蜗壳断面的数值求解

在略去证明条件下，下面给出断面上其他几何参数以表达的计算式。上部单圆弧的半径长记为，(3/(2tan))sin。等腰三角形的底边，也即下部等腰梯形的上底长记为，cos(3/(2tan))sin2，等腰三角形的高长记为1，1=sin(3/(2tan))sin2；等腰梯形高长记为2，2-1=-(3/(2tan)) sin2。过两切点、的水平线把断面分成了两部分，设在速度矩守恒条件下通过下部梯形和上部弓形的流量分别为1和2

求解一计算断面的核心任务是确定值，但是，在计算过程中又要用到值本身，因而这一值只能以逐次逼近方法获取。为此，在处理一断面前应假定一值。合理假定值的原则在后文叙述。

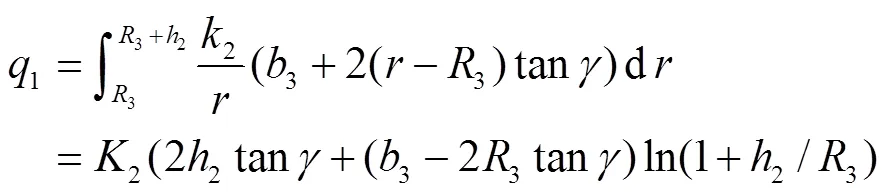
通过上部弓形的流量2只能获取数值解[24]。在图2中，以等距水平的平行线将之上的弓形部分划分成等份（≥300），得到个微矩形，它们有相等的高d，d=(+1)/=((3/(2tan)+)sin+(3/(2tanγ)+)sin2)/。

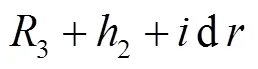
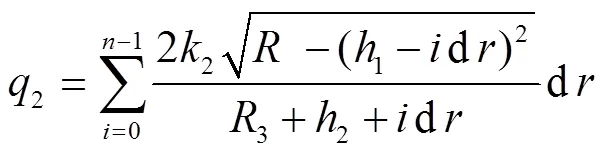
2.2 临界流量qcri的数值求解

1.1中所述的梯形弓形断面的应用要受到限制，因为这种结构允许的通过流量有一最小值。当图2中的断面退化为仅含一弓形，即形成弓形的单圆弧通过3两端点且与假想的方向不变的两直线腰相切时，以同一速度矩通过这一特殊断面的流量显然比任何一个含有下部梯形的断面要小一些，这一最小流量称临界流量q。这一流量也只能以数值求解方法获得。图3中即为这一特殊断面。

图3 通过临界流量的特殊断面

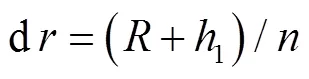
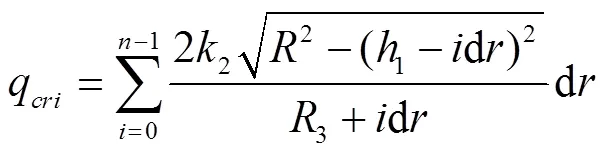
2.3 小流量断面几何参数的数值求解

如前文所述，蜗壳起始断面要求通过的流量q可能小于临界流量q，这时，可用如图4所示的曲边梯形形成这种小流量的断面。断面的两腰为过3两端点且与假想的与垂直方向夹角为的两射线相切的两圆弧。尽管断面上部分有一水平直线段，但由于以圆弧代替了传统梯形的直线型两腰及过渡圆弧，湿周因此有所减小。同时，在断面入口两圆弧切线夹角和仍为，避免了入口处由轴面突然扩散可能引起的脱流与旋涡。

图4 小流量断面

圆弧的圆心显然应在通过3两端点且与底边夹角为的射线上，如图4。如果确定了圆弧半径的长，则可确定断面几何形态，绘形断面。为保证在速度矩守恒条件下通过断面的要求流量q,也必须以数值计算方法获取。

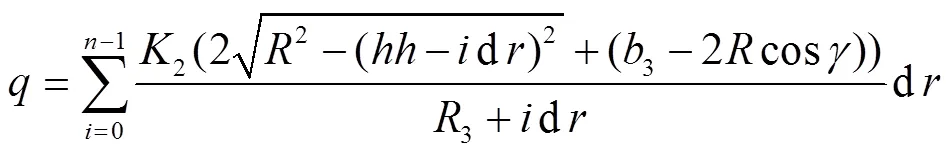
将所得值与本断面事先预定流量q比较，如果落入含有q的一个任意小的闭区间，说明事先假定的值正确，输出值。否则应根据与q的比较关系，适当增大或减小值，重新计算，直到问题收敛为止。

2.4 蜗壳8个断面计算过程

根据已确定的23,3，值，计算蜗壳临界流量q，见1.2。确定8个断面各自应通过的流量q（=1,2,3…,8）。在求解某一断面时，应以此断面通过的流量q与临界流量q比较，如果q>q，则此断面应使用梯形弓形结构断面（见1.1）；反之，应使用曲腰梯形断面（见1.3）。可根据前文所述原理及计算步骤编写算法语言程序，以快速获得8个蜗壳断面的计算结果。

以本文介绍方法作为依据，改型设计了3台中比转速离心泵蜗壳。产品的验收试验在2级精度试验台上完成。试验台由中国农业机械化科学研究设计院设计并配置测试仪表及数据收集处理、特性曲线绘形等软件[25]。经计算比较，试验泵各蜗壳断面湿周都有不同程度的显著减小，结果导致各泵在大约0.6～1.4倍设计流量区域内，泵的扬程与效率都有所提高，在设计点附近的提高幅度均达到1.6%，证明本文所述的方法有一定工程应用价值。

3 结 论

离心泵螺旋形蜗壳轴面断面湿周值是影响蜗壳能量指标的重要因素，减少这一值对改善泵的水力效率有重要意义。在传统的蜗壳设计方法中，不论是使用速度系数法还是利用速度矩守恒原理，都未将减小蜗壳断面周长作为追求目标。本文提出了一有别于传统设计理念的蜗壳设计方法，方法的核心在于确保蜗壳的基本性能的同时，力求蜗壳断面湿周最小化以降低蜗壳中的水力损失，由此提升泵的效率性能。这一方法决定的蜗壳断面与传统蜗壳断面有较大的几何差异。本文利用速度矩守恒原则及等面积图形中圆具有最小周长的特点，形成2种特殊的结构以分别适应大流量及小流量蜗壳断面。两种断面的几何特性决定了断面参数无解析解，为此，本文给出了2种断面的几何参数数值解的求解原理及过程。事实证明，本文提出的方法对改善泵效率有积极效果，在设计点附近提高幅度均达到1.6%。

[1] 孟根其其格，谭磊，曹树良，等. 离心泵蜗壳内非定常流动特性的数值模拟及分析[J]. 机械工程学报，2015，51(22)：183－190.

Meng Gengqiqige, Tan Lei, Cao Shuliang, et al. Numerical simulation and analysis of unsteady flow characteristics in centrifugal pump volute[J]. Chinese Journal of Mechanical Engineering, 2015, 51(22): 183－190. (in Chinese with English abstract)

[2] 徐伟利. 离心泵蜗壳八个断面的设计研究[J]. 农业工程学报，1996，12(2)：79－100.

Xu Liwei. Research and design of eight profiles of flow duct in spiral casing of centrifugal pumps[J]. Transaction of the Chinese Society of Agricultural Engineering (Transaction of the CSAE), 1996, 12(2): 79－100. (in Chinese with English abstract)

[3] 袁寿其，施卫东，刘厚林. 泵理论与技术[M]. 北京：机械工业出版社，2014：63－67.

[4] Lobanoff V S. Centrifugal Pumps-Design and Application[M]. Houston: Gulf Publishing Company, 1992: 50－54.

[5] 严敬，陈丹，赵琴，等. 对国外一种最新离心泵蜗壳设计资料的分析[J]. 水泵技术，2005(5)：12－13.

Yan Jing, Chen Dan, Zhao Qin, et al. Analysis about a new reference data for centrifugal pump volute design[J]. Pump Technology, 2005(5): 12－13. (in Chinese with English abstract)

[6] Johann F G. Centrifugal Pumps[M]. New York: Springer Berlin Heideburg Press, 2008: 403－413.

[7] Hamed A, Sseyyed A N, Medhrdal R, et al. Effect of the volute tongue profile on the performance of a low specific speed centrifugal pump[J]. Power and Energy (Part A), 2015, 229(2): 210－220.

[8] 高江永，郭振苗. 离心泵叶轮与蜗壳设计几何参数的优化研究[J]. 水泵技术，2007(4)：6－9.

Gao Jiangyong, Guo Zhenmiao. Optimal research on geometrical parameters of centrifugal impellers and volute[J]. Pump Technology, 2007(4): 6－9. (in Chinese with English abstract)

[9] 严敬，王建宇. 数值求解矩形断面蜗壳[J]. 排灌机械，1997(1)：8－11.

Yan Jing, Wang Jianyu. A numerical programme for rectangular volute casing section[J]. Drainage and Irrigation Machinery, 1997(1): 8－11. (in Chinese with English abstract)

[10] 严敬，王春志. 叶片泵梯形蜗壳断面的数字积分求解[J].流体机械，1995，23(3)：31－34.

Yan Jing, Wang Chunzhi. A numerical integration program for volute casing sections[J]. Fluid Machinery, 1995, 23(3): 31－34. (in Chinese with English abstract)

[11] 严敬. 低比转速离心泵[M]. 成都：四川科学技术出版社，1998：200－209.

[12] 许维德. 流体力学[M]. 北京：国际工业出版社，1979：219－224.

[13] 严敬，赵琴，杨小林. 工程流体力学[M]. 重庆：重庆大学出版社，2008：61－65.

[14] 罗乾惕，程兆雪，谢永曜. 流体力学[M]. 北京：机械工业出版社，2011：56－69.

[15] 查森. 叶片泵原理及水力设计[M]. 北京：机械工业出版社，1989：104－109.

[16] 洛马金A A. 离心泵与轴流泵（中译本）[M]. 北京：机械工业出版社，1978：189－192.

[17] Frank U W. Fluid Mechanics[M]. 北京：清华大学出版社，2004: 361－369.

[18] Douglas J F. Fluid Mechanics[M]. Pitman Publishing Limited, 1979: 252－254.

[19] 丁成伟. 离心泵与轴流泵[M]. 北京：机械工业出版社，1978：19－24.

[20] 关醒凡. 泵的理论与设计[M]. 北京：机械工业出版社，1987：13－15.

[21] 关醒凡. 现代泵理论与设计[M]. 北京：中国宇航出版社，2011：305－312.

[22] 特罗斯科兰斯基A T（波）. 叶片泵计算与结构（中译本）[M]. 北京：机械工业出版社，1984：187－194.

[23] 吴玉林，刘娟，陈铁军，等. 叶片泵设计与实例[M]. 北京：机械工业出版社，2011：92－97.

[24] 邓建中，葛仁杰，程正兴. 计算方法[M]. 西安：西安交通大学出版社，1993：152－157.

[25] GB/T 3216-2005. 回转动力泵水力性能验收试验[S]. 北京：中国标准出版社，2006.

Geometric parameters numerical calculation for energy saving volute cross sections of centrifugal pumps based on conservation of angular momentum

Yan Jing1,2, Hu Zanao1,2, Liu Xiaobing1,2, Zhou Xucheng3

(1.(),610039,; 2.610039,; 3.610300,)

Volute casings are extensively used in centrifugal pumps. Minimizing hydraulic losses generated in casings is an effective approach to improve pump efficiency. After water from impellers enters volute casings, as no external forces do work on the water, mechanical energy of water can’t be increased. On the contrary, energy dissipation is inevitable due to the friction in casings. Based on previous research, it is found that hydraulic losses in volute can account for half of the total losses in the pump. Analysis revealed that, as the flow in the volute is fully rough flow of high Reynolds number, the friction loss is independent of Reynolds number, but is only determined by the relative roughness of casing wall and is proportional to the length of wetted perimeters of volute cross sections. However, in 2 leading conventional designs, i.e. the calculation based on statistical data and the theorem of conservation of angular momentum, the relationship between perimeters of casing cross sections and friction losses is always neglected and no effort has been made to shorten the perimeters as a measure to increase pump efficiency. In this paper, we proposed a novel method to minimize the cross sectional perimeters and the friction losses in the volute. In all figures with identical area, circle has the shortest perimeter. The new design method provided in this paper takes the geometrical advantages of circles and forms new volute cross section shapes, which is different from the commonly used traditional trapezoidal section. In meridional sections, as streamlines of flow from the impeller can not change their directions abruptly, 2 eddies may appear at volute entrance if the volute section is constructed using circles. That is why full circles are not applicable for pump volute design. In order to make use of circle advantages and avoid its side effect, this paper suggested 2 types of volute sections, which are neither circular nor trapezoidal. The flow rates passing different volute sections are not identical and are related to the section positions in the volute. For high flow rate sections, the new sections involve a trapezoid located at lower portion and a single arc located at upper portion, while for low flow rate sections, the sections are formed by quadrangles with curved sides. It is evident that the perimeters of both types of new cross sections are shorter than the corresponding perimeters of conventional trapezoidal sections. The volute section outlines are controlled by its geometrical parameters. The first step in the volute design process is calculating all these parameters. As the theorem of conservation of angular momentum is widely used for volute design, the sectional parameters in this paper are obtained based on this theorem. Due to the complexity of both types of volute cross sections, it is impossible to gain analytical solutions of the section parameters. Therefore, numerical calculations are employed for parameter establishment. The flow circulation at impeller exit at design point is determined, as well as the entrance width of the volute cross sections, the angle between 2 volute sides in the meridional section and the vertical plane, and the radius of the base circle; and among all geometrical parameters to be decided, only one parameter is dominant and others can be obtained by this crucial parameter. In the calculation process for a particular section of any type, the first step is to assume the dominant parameter and divide the section into finite small elements. The second step is to calculate the flow rates passing all individual elemental areas based on the theorem of conservation of angular momentum. The sum of all flow rates is the total discharge passing the section considered. The last step, in terms of the comparison between the calculated total flow rate and the specified flow rate for the particular section, is to adjust the previously assumed parameter properly and repeat the computing process until 2 flow rates become identical. As a result, the last assumed value for the parameter is the final solution. The principles and the detailed numerically calculating procedures for 2 types of cross sections are presented in this paper. Tests indicated that expected results can be achieved by using the new approach described in the paper, and the new method is applicable in volute designs.

centrifugal pumps; design; volute; geometrical parameters; numerical calculation

10.11975/j.issn.1002-6819.2017.20.007

TH311

A

1002-6819(2017)-20-0056-05

2017-05-18

2017-08-31

国家自然科学基金资助项目（51279172）；流体及动力机械教育部重点实验室（西华大学）项目（SZJJ2015-41）

严 敬，教授，主要从事叶片泵过流部件设计新方法研究。 Email：jingyan16@aliyun.com

严 敬，胡赞熬，刘小兵，周绪成. 基于速度矩守恒的离心泵节能蜗壳断面几何参数求解[J]. 农业工程学报，2017，33(20)：56－60. doi：10.11975/j.issn.1002-6819.2017.20.007 http://www.tcsae.org

Yan Jing, Hu Zanao, Liu Xiaobing, Zhou Xucheng. Geometric parameters numerical calculation for energy saving volute cross sections of centrifugal pumps based on conservation of angular momentum[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(20): 56－60. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.20.007 http://www.tcsae.org