求解一类可分离凸规划的对偶显式模型DP-EM方法1)

隋允康 彭细荣

∗(北京工业大学工程数值模拟中心，北京100022)

†(湖南城市学院土木工程学院，湖南益阳413000)

生物、工程及交叉力学

求解一类可分离凸规划的对偶显式模型DP-EM方法1)

隋允康∗,2)彭细荣†,3)

∗(北京工业大学工程数值模拟中心，北京100022)

†(湖南城市学院土木工程学院，湖南益阳413000)

推导对偶目标函数的精确显式表达式，可选用更多成熟高效的求解方法，从而进一步提高了非线性规划对偶理论求解结构拓扑优化问题的效率.研究工作来源于非线性凸规划同其对偶规划的间隙为零，可以等价转化为对偶问题求解，通常可以大大地缩小问题的规模，可是二者不具有显式关系却影响了对偶解法的应用.所幸的是，结构优化当中一大类问题包括连续体结构拓扑优化问题，不仅具有凸性，而且具有变量可分离性，于是原变量和对偶变量之间有了显式关系，因此，对偶解法成了38年来被应用的有效方法之一.然而长期以来，对偶问题的目标函数并不是显式，这缘于含参数的极小化问题导致目标函数为隐式表达，常见的显式化方法是进行二阶近似.本文突破了对偶问题难以显式化只能采用近似显式的定势，将我们提出的“对偶规划--显式模型”(DP-EM)方法应用于连续体结构拓扑优化，并与对偶序列二次规划(DSQP)算法及移动渐近线(MMA)算法为求解器的方法进行计算效率对比，结果显示：(1)MMA算法比DP-EM算法和DSQP算法的外部迭代次数均多；(2)DP-EM算法与DSQP算法外循环次数相同，而内循环数显著减少.说明了DP-EM算法具有显式对偶函数的优势.

对偶目标显式模型化，可分离凸规划，结构拓扑优化，对偶序列二次规划方法，移动渐近线方法

引言

结构拓扑优化已经提出了大量的研究方法，比如均匀化方法[1]、变密度法[2]、ICM法[3]、进化结构优化方法[4]、水平集法[5]、相场法[6]及拓扑导数法[78]等，综述文献可参考Sigmund等[9]及Joshua等[10]，专著有Bendsoe等[11]的变密度法及隋允康等[12]的ICM法等.从优化模型的角度看，多数方法建立的数学模型归结为非线性规划问题，可以采用基于非线性规划理论的各种求解算法，其中也包括数学规划对偶理论的相关解法[13].早在结构拓扑优化之前的结构截面优化研究中，对偶规划解法就已经被关注，最典型的是1979年Fleury发表的工作，把凸规划的对偶规划解法作为新方法介绍到结构优化领域，并且用于求解桁架截面优化问题[14].

较之含很多约束条件的原问题，对偶问题只含有非负对偶变量条件，称为拟无约束规划，只要稍微修正一下，无约束规划的寻优算法就可以应用，这是该方法的优势.美中不足的是，对偶目标函数只是隐函数形式，然而，却可以求出其一阶导数和二阶导数的数值表达式.因此，Fleury在文献[14]中介绍了寻优的一阶算法和二阶算法，二者都是无约束规划寻优的“上升算法”(即反向的“下降算法”).

钱令希团队于1980年就论证了求解结构桁架截面优化原问题和对偶问题的等价性[15]，并且指出：由于对偶问题变量的维数等于原问题的约束个数，通常会大大地缩小优化的规模，因此建议按对偶问题求解，然后通过Kuhn-Tucker条件建立原变量与对偶变量之间的显式关系，得到原问题的最优解.在对偶问题求解时，用Lemke算法或其他算法直接求解拟无约束的二次规划形式的对偶问题，较之Fleury采用的“上升算法”，二次规划算法简洁、方便和可靠.

在钱令希团队的一系列工作[3,1520]中，文献[15-17]阐发了桁架结构优化运用对偶问题求解的理论和方法，文献[18]将截面优化问题的对偶解法从文献[14-17]的杆单元推广到杆、膜、梁单元的组合结构，文献[3]则进一步推广到杆、膜、板、壳、梁单元的复杂组合结构，而且文献[18]和文献[3]分别把只适合杆单元[1417]的对偶函数的二阶导数公式做了相应的推广，文献[19-20]聚焦在二次规划，介绍了该团队的一系列工作：原问题的二次化、对偶问题的二次化、正定几何规划的二次化和缩并几何规划二次化.

隋允康从1995年就指导博士生和硕士生开始了结构拓扑优化ICM法的研究，限于篇幅，本文只列出相关的4篇文献[2124]，其他研究者如龙凯等也应用过ICM法[25].ICM方法建立优化模型后，都是将原问题转为对偶问题求解.原因在于：对偶变量的个数是原问题的有效约束数目，因而对偶问题的设计变量维数极大地降低，以连续体多位移约束的结构拓扑优化为例，假如有10000个单元，4个载荷工况下3点位移约束，实际有效约束最多只有12个，亦即最多12个对偶变量，而原问题却有10000个原变量.其中的奥妙就在于Kuhn-Tucker条件成为原变量与对偶变量之间显式关系的桥梁，从而大幅度地提高了求解效率.

基于ICM方法建立的优化模型，同结构截面优化的研究类似，难以求解出对偶目标函数的显式表达式，只得转而求其一阶导数和二阶导数，进而建立二次近似函数形式的对偶目标函数，形成对偶序列二次规划(DSQP)方法的求解算法[3,12]，取得了很好的求解效率.由于长期以来采用DSQP方法求解，加上对偶目标函数依然是一个含参数的极小化问题，因而形成了不求对偶问题的目标函数显式的定势.

本文从结构优化所建立的数学规划模型的特点出发，针对一大类常见的变量可分离的凸规划问题，突破了只是停留在对偶目标二阶近似的定势，推导得出了显式的对偶目标函数.在这一研究的基础上，提出了便捷求解的DP-EM(dual programmingexplicit model)方法，并将其应用于求解连续体结构的拓扑优化问题.本文将DP-EM方法与基于DSQP算法及MMA算法[26]的方法进行计算效率对比，结果显示DP-EM方法具有更高的求解效率.

1 对偶目标函数的显式化导致DP-EM方法

对于下列非线性规划

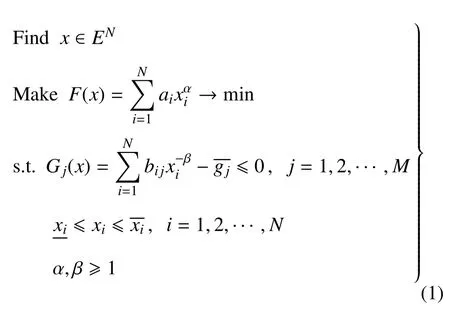
满足凸规划的条件.x为设计变量向量，N为设计变量数目，F(x)为目标函数，Gj(x)为不等式约束函数，M为约束数目，及为设计变量上下限，ai,bij,α及β分别为目标函数及约束函数中的系数及指数.

式(1)的拉格朗日函数为

其中λj为拉格朗日乘子.原问题(1)的对偶问题为

其中

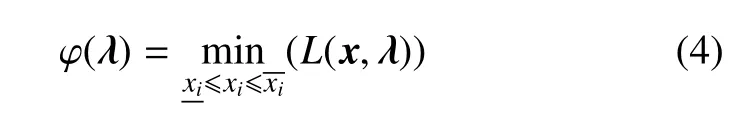
式(4)的Kuhn-Tucker条件为

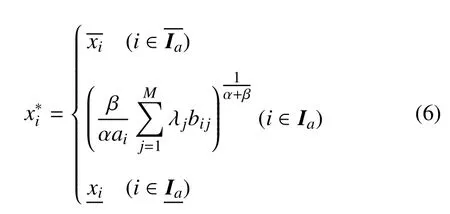
将式(6)代入式(4)得

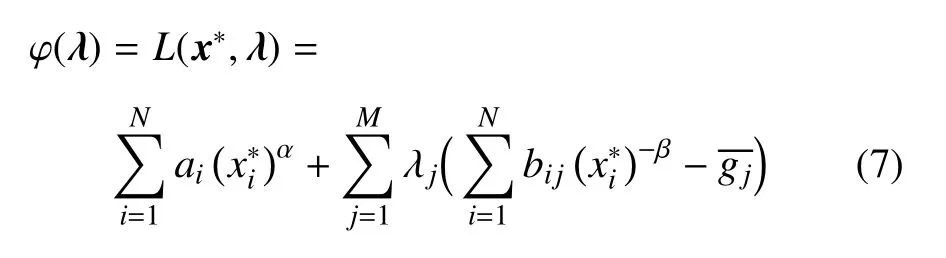
下面的工作是设法将式 (7)的表达式适当转化，从而将ϕ(λ)显式化.为此，将式(6)代入式(5)，其中，主动变量有下式

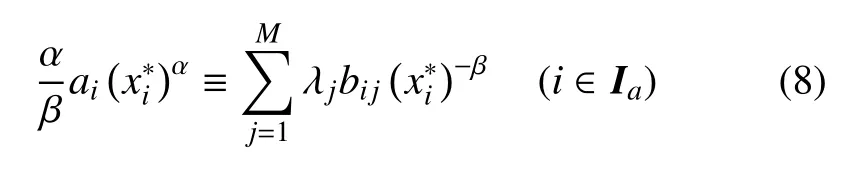
对于i∈Ia求和，得

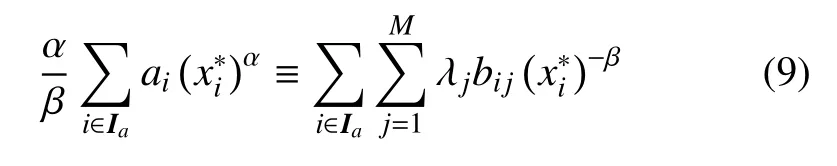
由式(9)可得

亦即

将式(11)代入式(7)，得

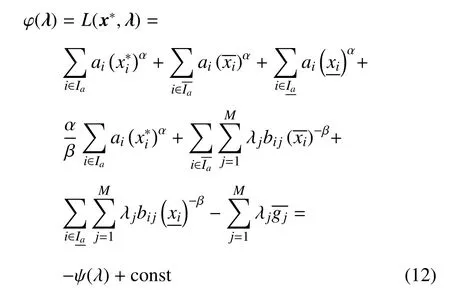
根据式(12)，对偶规划式(3)可以转化为等价的如下规划

注意式(15)具有显式目标函数式(13)，此规划在联合式(6)的情况下，可以在原问题的凸规则的前提下，得到原问题(1)的解.上述在理论上是完整的，用于结构优化的实际问题，只是多了一个建立优化模型的工作.

由于结构优化模型是近似的，建模伴随着求解，是一个大循环的迭代过程.另外，式(6)依赖于上被动变量集、主动变量集Ia和下被动变量集，在式(15)与式(6)的交替计算中，若变量集有变动，则每一轮大循环中出现小循环的过程.

鉴于每轮建模中，结构分析与敏度分析的昂贵，与建模得到 bij(i=1,2,···,N;j=1,2,···,M)构造式(13)，然后求解规划(15)，代回式(6)得到一个解，而不做小循环相比，采用小循环要好得多，可以充分利用好昂贵的模型.

至于规划(15)在显式(13)下的求解方法，比以往规划的SQP解法可以有更多的选择，不仅二次规划方法，还可以利用其他无约束优化方法，例如最速下降法、共轭梯度法、牛顿法、拟牛顿法(变尺度法)、信赖域法等等.尽管存在一个对偶变量非负约束，每次算出的λj只要为负值，就可以修正为0.此文中采用了MATLAB优化工具箱中的fmincon函数求解规划(15).

上述是针对一类变量可分离凸规划问题的建立模型和求解算法，为了方便于表述，称之为“对偶规划 --显式模型”(dual programming-explicit model，DPEM)方法.

2 DP-EM方法对于连续体结构拓扑优化的应用

以重量极小化受位移约束的连续体结构拓扑优化为例，应用ICM法建立拓扑优化模型，采用幂函数形式的过滤函数，单元重量及单元刚度用过滤函数识别

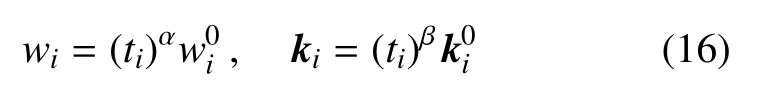
其中,wi及 ki为单元重量及单元刚度阵，及为单元固有重量及单元固有刚度阵.fw(ti)=(ti)α及分别为单元重量及单元刚度的幂函数形式过滤函数，本文取α=1及β=3.

结构总重量可表达为

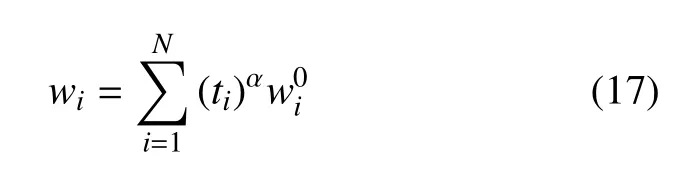
其中N表示单元拓扑设计变量的总数.

利用莫尔定理位移可表达为

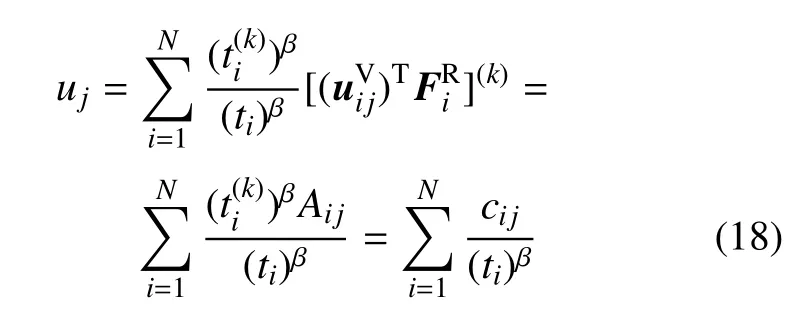
用ICM法建立的拓扑优化模型表示为

式中t=(t1,t2,···,tN)T是单元拓扑设计变量向量¯uj表示第 j号位移约束的上限.此模型与式(1)相同，不同之处只是设计变量x用拓扑设计变量t表达而已.

3 程序实现和算例比较

式(19)的结构拓扑优化问题即式(1)形式的可分离变量非线性规划，为了比较不同数学规划求解算法的效率，编制了3种求解方法的程序：本文提出的DP-EM方法对应的求解算法，以往的DSQP算法和移动渐近线(MMA)算法.DP-EM算法及DSQP算法采用自编的MATLAB函数，MMA算法采用文献[13]所公布的MATLAB代码.

3种算法的收敛准则采取连续二次迭代的最大设计变量差值小于设定的收敛精度

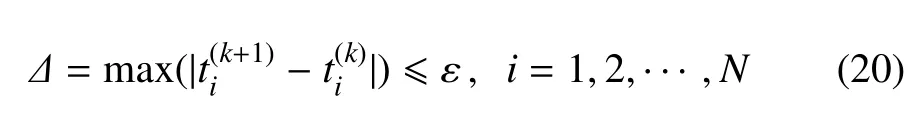
其中收敛精度ε在此文中取0.005.

连续体结构拓扑优化存在棋盘格现象及网格依赖等数值不稳定问题，消除此数值不稳定问题的一类典型方法是过滤法[9].本文采用对位移贡献系数Aij进行过滤处理的方法[22].

为了验证本文方法的正确性，采用网上公布的88行编码的连续体结构拓扑优化程序的优化结果，作为算例进行比较[27].不过，文献[27]求解的是体积约束下结构柔顺度极小问题，而本文求解的是位移约束下体积极小问题.

如何把88行程序的结果作为本文的算例？首先用88行程序算出一个最优拓扑构型结果，把其中拟作为位移约束点的位移作为算例的约束位移值，然后用本文的三种方法进行计算；最后把算例与文献[27]的结果对比看最后的拓扑构型是否相同.

算例1：MBB梁拓扑优化

MBB梁拓扑优化，基结构宽高比为6:1，无量纲集中载荷F=2作用于跨中顶点，左、右下角分别为铰支及滑动铰支约束，材料无量纲弹性模量E=1，泊松比0.3.取一半结构进行分析，计算简图如图1所示，采用60×20,150×50及300×100三种网格进行计算.

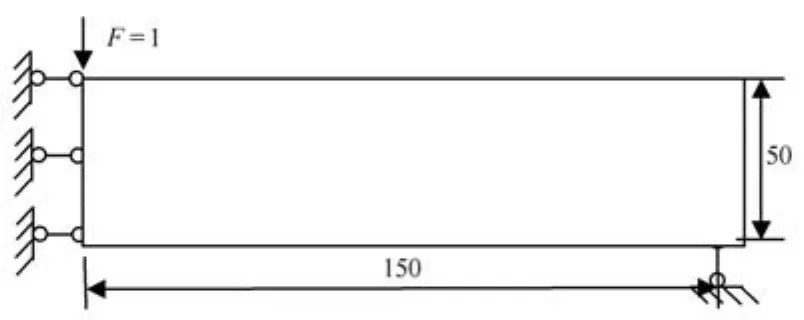
图1 150×50网格MBB梁问题取一半结构进行分析及优化时模型定义Fig.1 Half of structure for analysis and optimization of the MBB beam with 150×50 mesh

采用与文献[27]相同的数据，保留体积比0.5，采用敏度过滤，过滤半径为基结构高度的0.12倍，SIMP方法的惩罚因子取p=3，收敛精度分别取0.01及0.005.采用150×50网格按88行程序计算出来的体积约束下结构柔顺度极小化的最优拓扑图形如图2所示，两种精度下得到的最优拓扑图形相同，对应的最优目标函数值分别为219.52及219.57，相差很小.其中收敛精度为0.01时的结果与文献[27]是相同的.

收敛精度为0.005时对应的最优结构在力作用方向的位移值为219.57，以此位移值作为此算例位移约束下重量极小化问题中的位移约束值.

图2 150×50网格时文献[27]中88行代码得到的最优拓扑Fig.2 Optimal topologies obtained by the 88 lines of codes in the reference[27]for 150×50 mesh

不取收敛精度0.01对应的位移值作为约束，是考虑到MMA算法在此精度下得不到最优拓扑.当收敛精度取0.01时，不同方法得到的离散前的最优拓扑结构对比如表1所示，DP-EM算法及DSQP算法得到的最优拓扑相同，也与88行程序得到的最优拓扑相同，但与MMA算法得到的最优拓扑不相同.当收敛精度取0.005时，三种方法得到的最优拓扑均相同，如表2所示.离散后最优拓扑如表3所示.MMA算法需要设定更高的收敛精度才能得到最优拓扑，其在收敛精度为0.01时得到的拓扑并不是最优拓扑，而DP-EM算法及DSQP算法在低精度下即得到了最优拓扑，表现出了算法有更好的寻优能力.

表1 算例1不同求解算法离散前的最优拓扑结构对比(收敛精度0.01)Table 1 Comparison of optimal topologies obtained by di ff erent algorithms before discrete for the example 1(convergence precision takes 0.01)

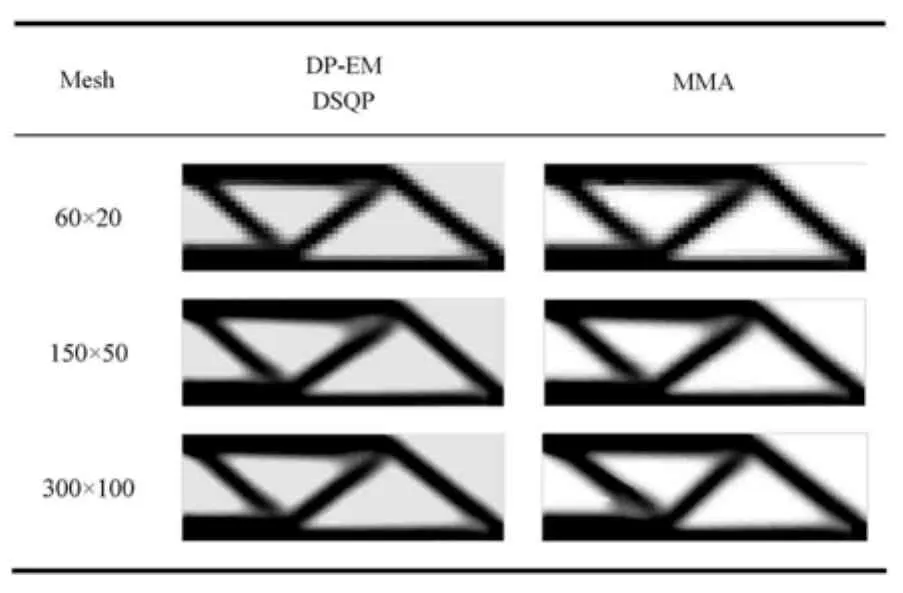
表2 算例1不同求解算法离散前的最优拓扑结构对比(收敛精度0.005)Table 2 Comparison of optimal topologies obtained by di ff erent algorithms before discrete for the example 1(convergence precision takes 0.005)

表3 算例1不同求解算法离散后的最优拓扑结构对比(收敛精度0.005)Table 3 Comparison of optimal topologies obtained by di ff erent algorithms before discrete for the example 1(convergence precision takes 0.005)

收敛精度为0.005时不同算法求解效率对比如表4所示.DP-EM算法及DSQP算法外循环迭代次数相同，均明显少于MMA算法，如图3所示.而内循环次数DP-EM算法比DSQP算法显著减少，DPEM每次内循环迭代3次或4次，而DSQP算法每次内循环迭代10次左右，如图4所示，可见通过对偶函数的显式化，可更快更好地得到对偶变量的最优解，从而显著地减少内循环次数.

此外，MMA算法随着单元数目(即设计变量数目)的增加，迭代次数增加，而DP-EM算法与DSQP算法则变化不大.所以，对大规模问题，DP-EM算法与DSQP算法的效率比MMA算法显著提升.

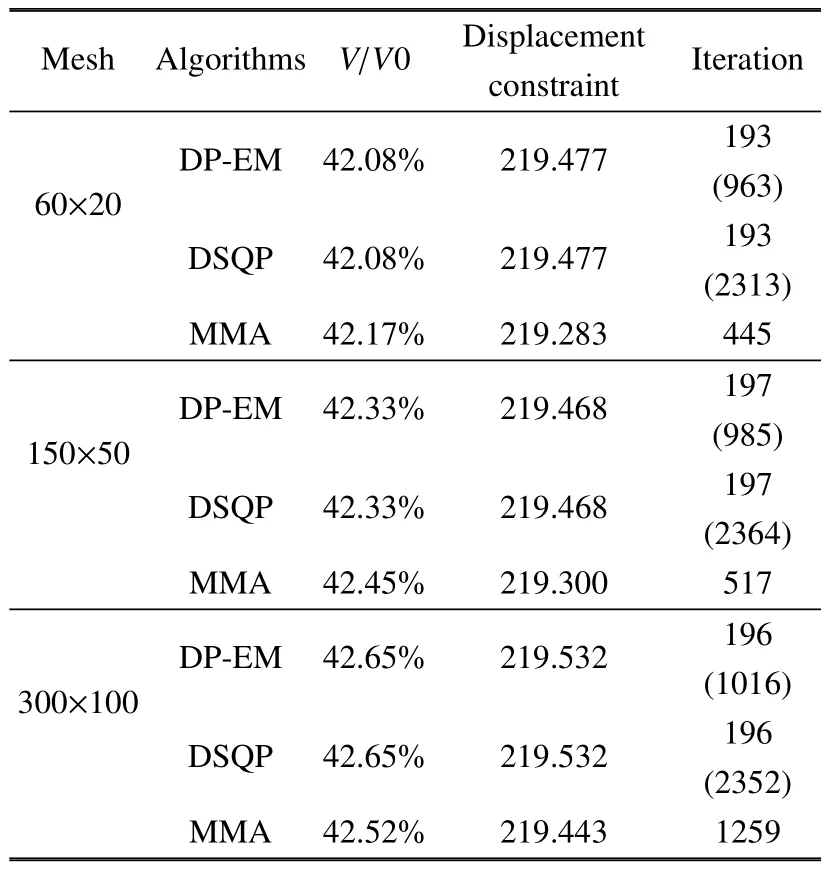
表4 算例1不同求解算法求解效率对比(收敛精度0.005)Table 4 Comparison of the solution efficiencies of di ff erent algorithms for the example 1(convergence precision takes 0.005)

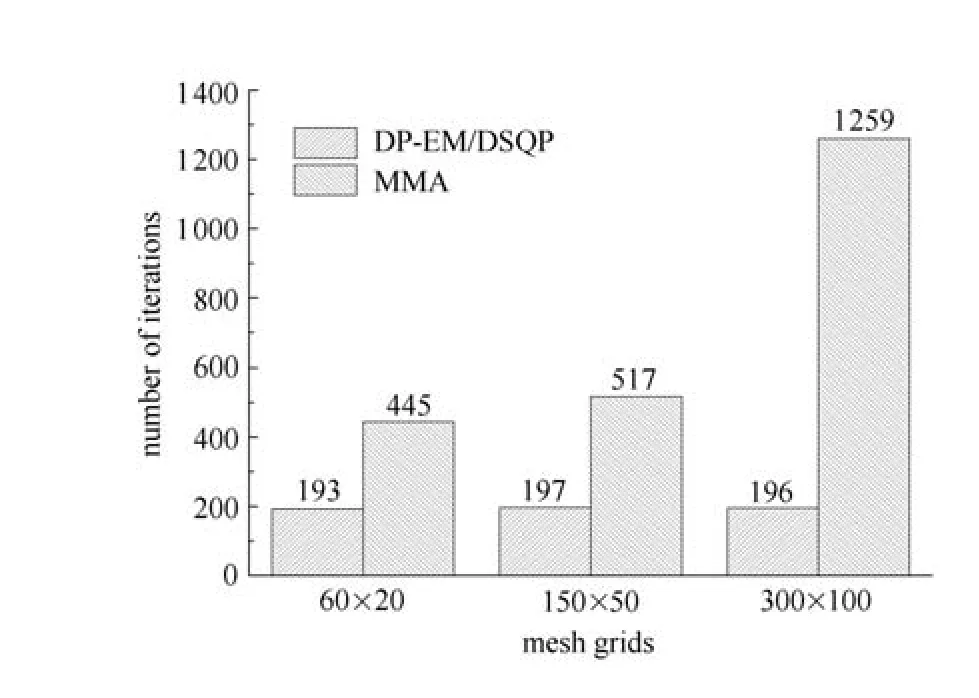
图3 DP-EM及DSQP与MMA迭代次数比较Fig.3 Comparison of the iterations for DP-EM,DSQP and MMA

图4 DP-EM与DSQP内循环迭代次数比较Fig.4 Comparison of the iterations of the internal loops for the DP-EM and DSQP

算例2：多工况多位移约束拓扑优化问题[27]

一正方形平板结构如图5所示，载荷工况有2种，工况1为一集中载荷F1=1竖直向上作用于右上角;工况2为一集中载荷F2=1竖直向下作用于右下角.平板左边界固定约束，材料弹性模量E=1，泊松比0.3.采用75×75,150×150及300×300三种网格进行计算.

图5 150×150网格正方形平板拓扑优化问题定义Fig.5 De fi nition of the topology optimization problem of a square plate with 150×150 mesh

采用与文献[27]相同的数据，两个工况柔顺度采用0.5的权重进行加权组合成单一柔顺度目标，保留体积比0.4，采用敏度过滤，过滤半径为基结构设计的0.04倍，SIMP方法的惩罚因子取p=3，收敛精度分别取0.01及0.005.采用150×150网格按88行程序计算出来的体积约束下结构柔顺度极小化的最优拓扑图形如图6所示，两种精度下得到的最优拓扑图形不相同，对应的最优目标函数值分别为69.20及68.83，目标函数值相差很小，但拓扑图形相差很大.其中收敛精度为0.01时的结果与文献[27]是相同的，但显然，这一精度下得到的并非最优拓扑图形.因而，此算例的比较对象取收敛精度为0.005时的结果，对应的最优结构在两工况下集中力作用方向的位移值均为34.42，以此位移值作为此算例重量极小化问题中的位移约束值，即位移约束F1及F2作用方向位移小于34.42.

三种求解算法在收敛精度为0.005时得到的最优拓扑相同，与88行程序计算在收敛精度0.005时的最优拓扑形式相同，如表5所示.不同算法求解效率对比如表6、图7及图8所示，外循环迭代次数DP-EM算法及DSQP算法相同，均比MMA算法少,但没有算例1中差别那么大.而内循环次数DP-EM算法明显比DSQP算法少.

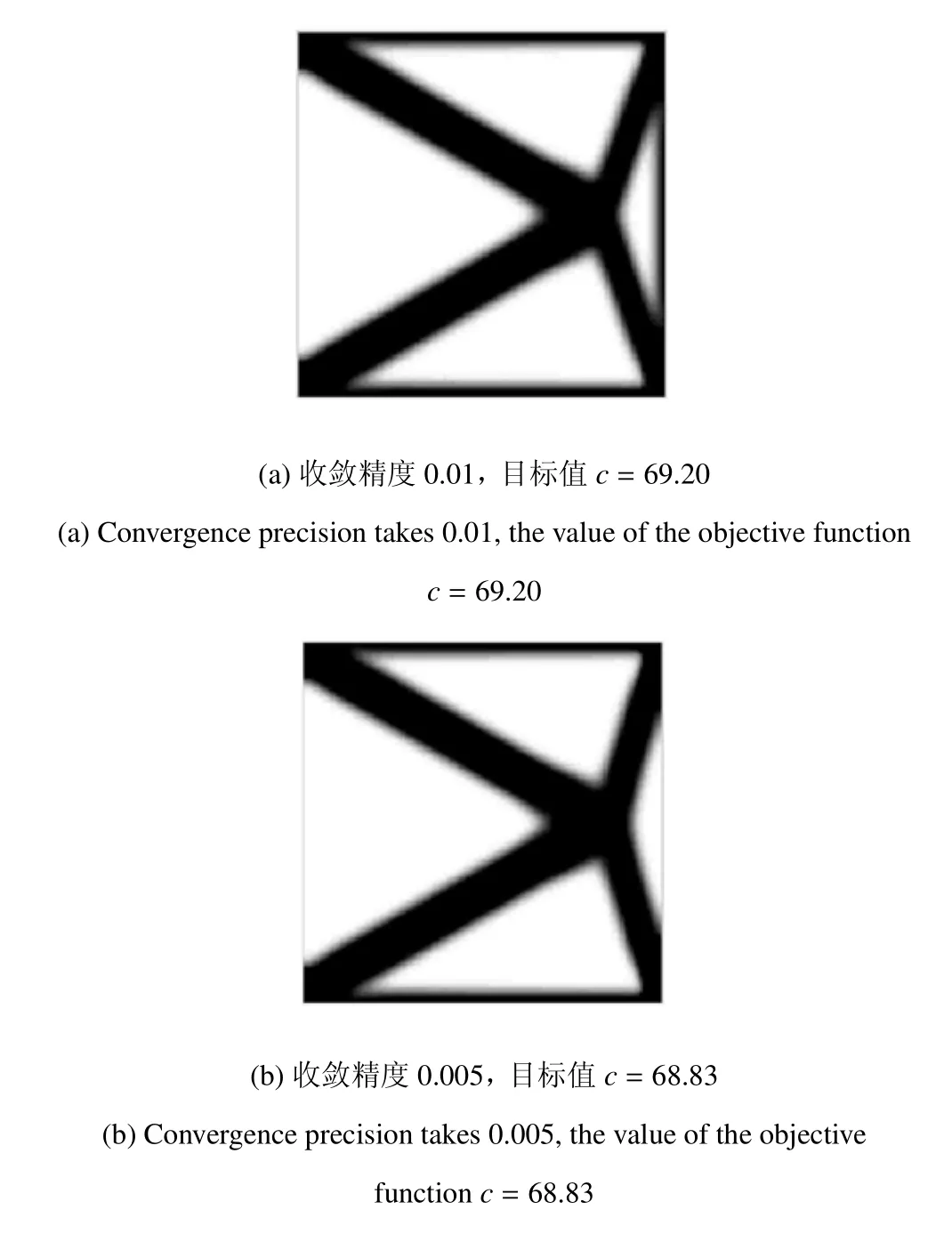
图6 150×150网格时文献[27]中88行代码得到的最优拓扑Fig.6 Optimal topologies obtained by the 88 lines of codes in the Ref.[27]for 150×150 mesh

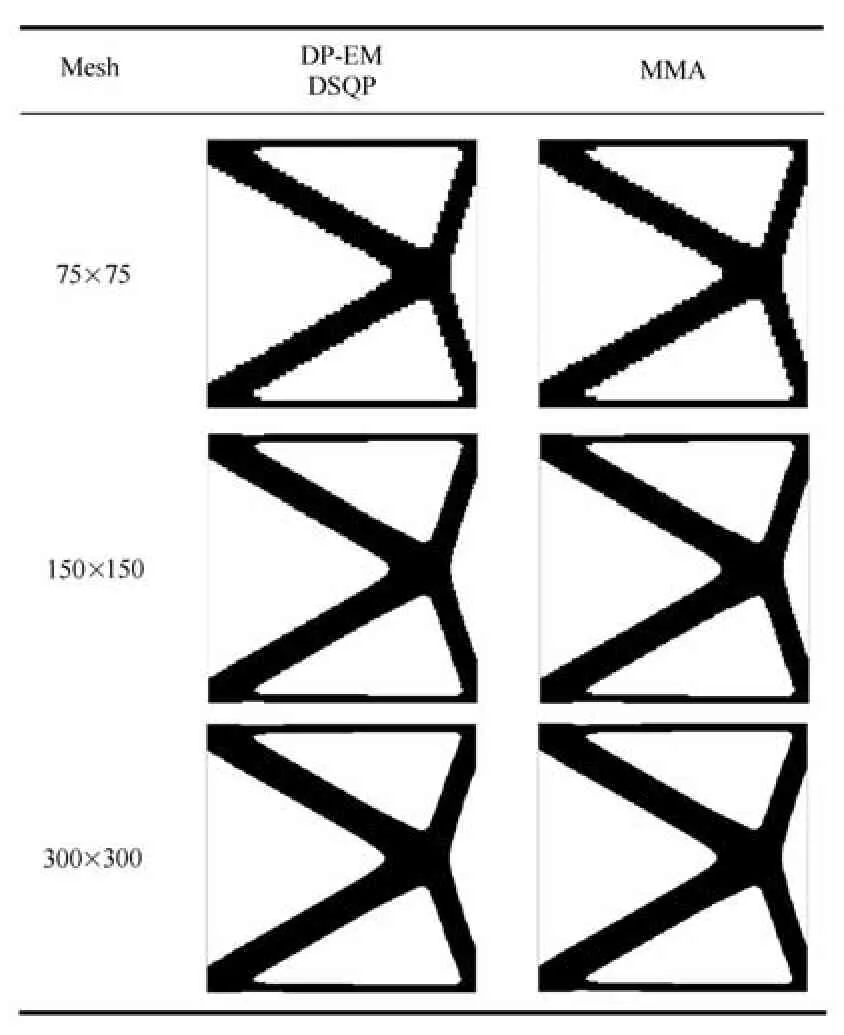
表5 算例2不同求解算法最优拓扑结构对比Table 5 Comparison of optimal topologies obtained by di ff erent algorithms for the example 2

表6 算例2不同求解算法求解效率对比Table 6 Comparison of the solution efficiencies of di ff erent algorithms for the example 2

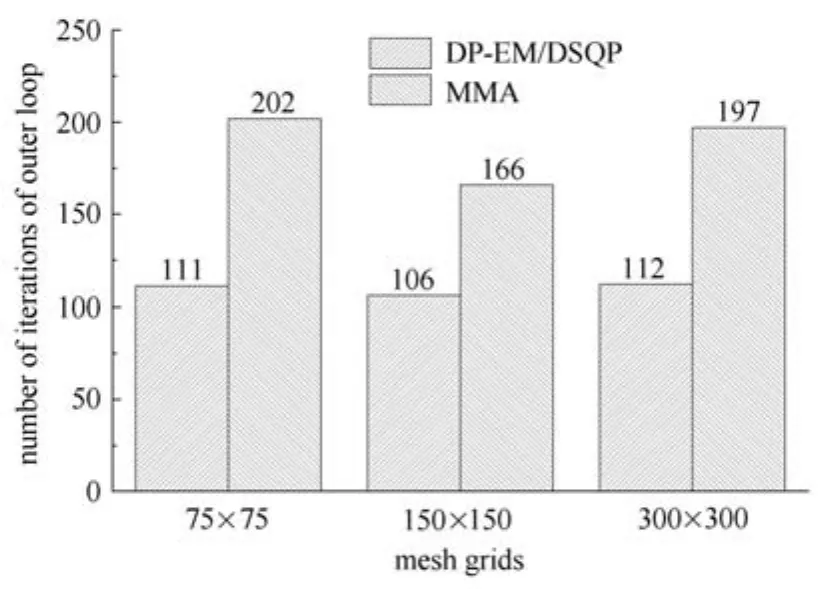
图7 DP-EM及DSQP与MMA迭代次数比较Fig.7 Comparison of the iterations for DP-EM,DSQP and MMA

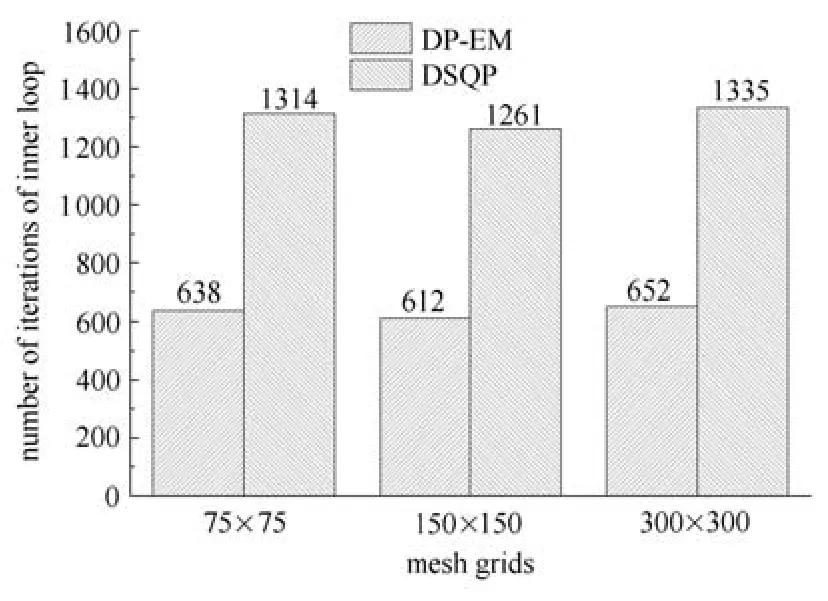
图8 DP-EM与DSQP内循环迭代次数比较Fig.8 Comparison of the iterations of the internal loops for the DP-EM and DSQP

4 结论

针对可分离变量的凸规划问题，本文推导了其对偶目标函数的显式表达式，并提出了对应的DPEM方法及其求解算法，付诸连续体结构拓扑优化问题，取多工况位移约束下重量目标极小化问题编程，将DP-EM算法与DSQP算法及MMA算法进行了效率对比.

(1)在所有算例的计算中，三种算法皆与文献[15]的最后构型相同，表明本文的方法及其程序通过了验证.

(2)DP-EM算法与DSQP算法相比外循环次数相同，是由于其求解的是同一数学规划模型，只是优化求解器不同.DP-EM算法的内循环数显著少于DSQP算法，显示了DP-EM算法得到显式对偶函数的优势，而DSQP算法应用二阶近似迭代逼近的目标函数，故计算效率逊色.

(3)MMA算法比DP-EM算法和DSQP算法的外部迭代次数亦即结构分析次数多，是因为MMA算法仅利用了原优化模型的目标函数及约束函数的一阶敏度信息，近似程度比较低.

(4)从科学研究方法论看，获得准确的显式模型优于近似的逼近模型，而能够做到的首要条件是突破“不可能做”的思维定势，从而别开生面地走出自己的路径.进一步拓宽DP-EM方法的工作正在进行，研究结果将会陆续发表.

1 Bendsoe MP,Kikuchi N.Generating optimal topologies in structural design using a homogenization method.Computer Methods in Applied Mechanics and Engineering,1988,69:197-224

2 Mlejnek HP.Some aspects of the genesis of structures.Structural Optimization,1992,5:64-69

3隋允康.建模·变换·优化——结构综合方法新进展.大连:大连理工大学出版社,1996(Sui Yunkang.Modelling,Transformation,and Optimization–New Developments of Structural Synthesis Method.Dalian:Dalian University of Technology Press,1996(in Chinese))

4 Xie YM,Steven GP.A simple evolutionary procedure for structural optimization.Comput Struct,1993,49:885-896

5 Osher S,Sethian J.Fronts propagating with curvature dependent speed-algorithms based on hamilton-jacobi formulations.J Comput Phys,1988,79(1):12-49

6 Bourdin B,Chambolle A.Design-dependent loads in topology optimization.ESAIM:Control,Optimisation and Calculus of Variations,2003,9(8):19-48

7 Eschenauer HA,Kobelev VV,Schumacher A.Bubble method for topology and shape optimization of structures.Structural Optimization,1994,8(1):42-51

8 Norato J,Bendsøe M,Haber R,et al.A topological derivative method for topology optimization.Structural and Multidisciplinary Optimization,2007,33(4-5):375-386

9 Sigmund O,Maute K.Topology optimization approaches—A comparative review.Structural Multidisciplinary Optimization,2013,48(6):1031-1055

10 Joshua DD,Ramana VG.A survey of structural and multidisciplinary continuum topology optimization:Post 2000.Structural and Multidisciplinary Optimization,2014,49:1-38

11 Bendsoe M P,Sigmund O.Topology Optimization:Theory,Methods and Applications.New York:Springer Berlin Heidelberg,2003

12隋允康,叶红玲.连续体结构拓扑优化的ICM方法.北京:科学出版社,2013(Sui Yunkang,Ye Hongling.Continuum Topology Optimization Methods ICM.Beijing:Science Press,2013(in Chinese))

13 Bazaraa MS,Shetty CM.Nonlinear Programming,Theory and Algorithms.[s.l.]John Wiley&Sons,1979

14 Fleury C.Structural weight optimization dual method of convex programming.International Journal for Numerical Methods in Engineering,1979,14(12):1761-1783

15钱令希，钟万勰，隋允康等.多单元、多工况、多约束的结构优化程序系统DDDU.大连工学院学报,1980,19(4):1-17(Qian Lingxi,Zhong Wanxie,Sui Yunkang,Zhang Jindong.Optimum design of structures with multiple types of element under multiple loading cases and multiple constraints-program system DDDU.Journal of Dalian Institute of Technology,1980,19(4):1-17(in Chinese))

16 Qian LX，Zhong WX,Sui YK,et al.Efficient optimum design of structures program DDDU.Computer Methods in Applied Mechanics and Engineering,1982,30(2):209-224

17钱令希.工程结构优化设计.北京:水利电力出版社,1983(Qian Lingxi.Optimization Design for Engineering Structures.Beijing:Water Conservancy and Electric Power Press,1983(in Chinese))

18隋允康,钟万勰,钱令希.杆--膜--梁组合结构优化的DDDU-2程序系统.大连工学院学报,1983,22(1):21-36(Sui Yunkang,Zhong Wanxie,Qian Lingxi.Optimum design of structures composed of bars-membranes-beams program system DDDU-2.Journal of Dalian Institute of Technology,1983,1:21-36(in Chinese))

19钱令希,钟万勰,程耿东等.工程结构的序列二次规划.固体力学学报,1983,22(4):469-480(Qian Lingxi,Zhong Wanxie,Cheng Gengdong,et al.Sequential quadratic programming approach in engineering structural optimization.Acta Mechanica Solida Sinica,1983,22(4):469-480(in Chinese))

20 Qian LX,Zhong WX,Cheng GD,et al.An approach to structural optimization-SQP(sequential quadratic programming).Engineering Optimization,1984,1(8):83-100

21隋允康，杨德庆，孙焕纯.统一骨架与连续体的结构拓扑优化的 ICM理论与方法.计算力学学报,2000,1(17):28-33(Sui Yunkang,Yang Deqing,Sun Huanchun.Uniform ICM theory and method on optimization of structural topology for skeletonal and continuum structures.Chinese Journal of Computational Mechanics,2000,1(17):28-33(in Chinese))

22隋允康,彭细荣.结构拓扑优化ICM方法的改善.力学学报,2005,37(2):190-198(Sui Yunkang,Peng Xirong.The improvement for the ICM method of structural topology optimization.Acta Mechanica Sinica,2005,37(2):190-198(in Chinese))

23隋允康,宣东海,尚珍.连续体结构拓扑优化的高精度逼近ICM方法.力学学报,2011,43(4):716-724(Sui Yunkang,Xuan Donghai,Shang Zhen.ICM method with high accuracy approximation for topology optimization of continuum structures.Chinese Journal of Theoretical and Applied Mechanics,2011,43(4):716-724(in Chinese))

24叶红玲,沈静娴,隋允康.频率约束的三维连续体结构动力拓扑优化设计.力学学报,2012,44(6):1037-1045(Ye Hongling,ShenJingxian,SuiYunkang.Dynamictopologicaloptimaldesignof three-dimensional continuum structures with frequency constraints.Acta Mechanica Sinica,2012,44(6):1037-1045(in Chinese))

25龙凯,王选,韩丹.基于多相材料的稳态热传导结构轻量化设计.力学学报,2017,49(2):359-366(Long Kai,Wang Xuan,Han Dan.Structural light design for steady heat conduction using multimaterial.Chinese Journal of Theoretical and Applied Mechanics,2017,49(2):359-366(in Chinese))

26 Svanberg K.Method of moving asymptotes–a new method for structural optimization.International Journal for Numerical Methods in Engineering,1987,24(2):359-373

27 Andreassen E,Clausen A,Lazarov BS,et al.Efficient topology optimization in MATLAB using 88 lines of code.Structural Multidisciplinary Optimization,2011,43(1):1-16

A DUAL EXPLICIT MODEL BASED DP-EM METHOD FOR SOLVING A CLASS OF SEPARABLE CONVEX PROGRAMMING1)

Sui Yunkang∗,2)Peng Xirong†,3)∗(Numerical Simulation Center for Engineering，Beijing University of Technology，Beijing 100022，China)
†(School of Civil Engineering，Hunan City University，Yiyang 413000，Hunan，China)

An explicit exact formula is derived for the objective function of the dual model of a class of separable convex programming problems.It makes more mature and efficient methods can be chose to solve the dual model.Therefore,the advantage of applying the duality theory of nonlinear programming to efficiently solve structural topology optimization problems is fully exploited.The research work is rooted in that the gap of a nonlinear convex programming with its dual programming is zero.Solving original programming can be equivalently transformed into solving its dual programming.The scale of the solved programming can usually be reduced greatly.But an explicit relationship is not existed between the original programming and dual programming has a ff ected the application of the dual solution algorithm.Fortunately,the programming models of a large class of structural optimization problems,including the continuum topology optimization,are convex and separable.And an explicit relationship between the original variables and their dual variables is existed;therefore,the dual solution algorithm has become one of the e ff ective methods for 38 years.However,the objective function of the dual problem is not explicit for a long time.It is because the dual problem is a parametric minimization problem which leads to the objective function is expressed as an implicit expression.The common explicit expression for the dual objective function is a two-order approximation.The regular thinking tendency that the dual problem is too difficult to be expressed explicitly and can only be expressed approximately is breakthrough.A dual programming explicit model(DP-EM)method is put forward for the topology optimization of continuum structures.Comparison of computational efficiency among the DP-EM method,the dual sequential quadratic program(DSQP)method and the method of moving asymptotes(MMA)is presented.The results showed that:(1)more external iterations are needed for the MMA algorithm than the DP-EM algorithm and DSQP algorithm;(2)same external iterations are needed for the DP-EM algorithm and DSQP algorithm,but internal iterations is less for the DP-EM method.It shows the advantage of the DP-EM algorithm due to its explicit dual function.

explicit dual objective function,separable convex programming,structural topology optimization,dual sequential quadratic program method,method of moving asymptotes

O343.1

A

10.6052/0459-1879-17-176

2017–05–13收稿，2017–08–15 录用,2017–08–17 网络版发表.

1)国家自然科学基金(11672103)和湖南省自然科学基金(2016JJ6016)资助项目.

2)隋允康，教授，主要研究方向：结构优化.E-mail:ysui@bjut.edu.cn

3)彭细荣，副教授，主要研究方向：结构优化.E-mail:pxr568@163.com

隋允康,彭细荣.求解一类可分离凸规划的对偶显式模型DP-EM方法.力学学报,2017,49(5):1135-1144

Sui Yunkang,Peng Xirong.A dual explicit model based DP-EM method for solving a class of separable convex programming.Chinese Journal of Theoretical and Applied Mechanics,2017,49(5):1135-1144