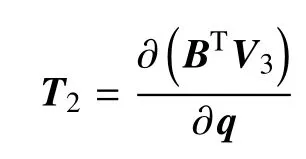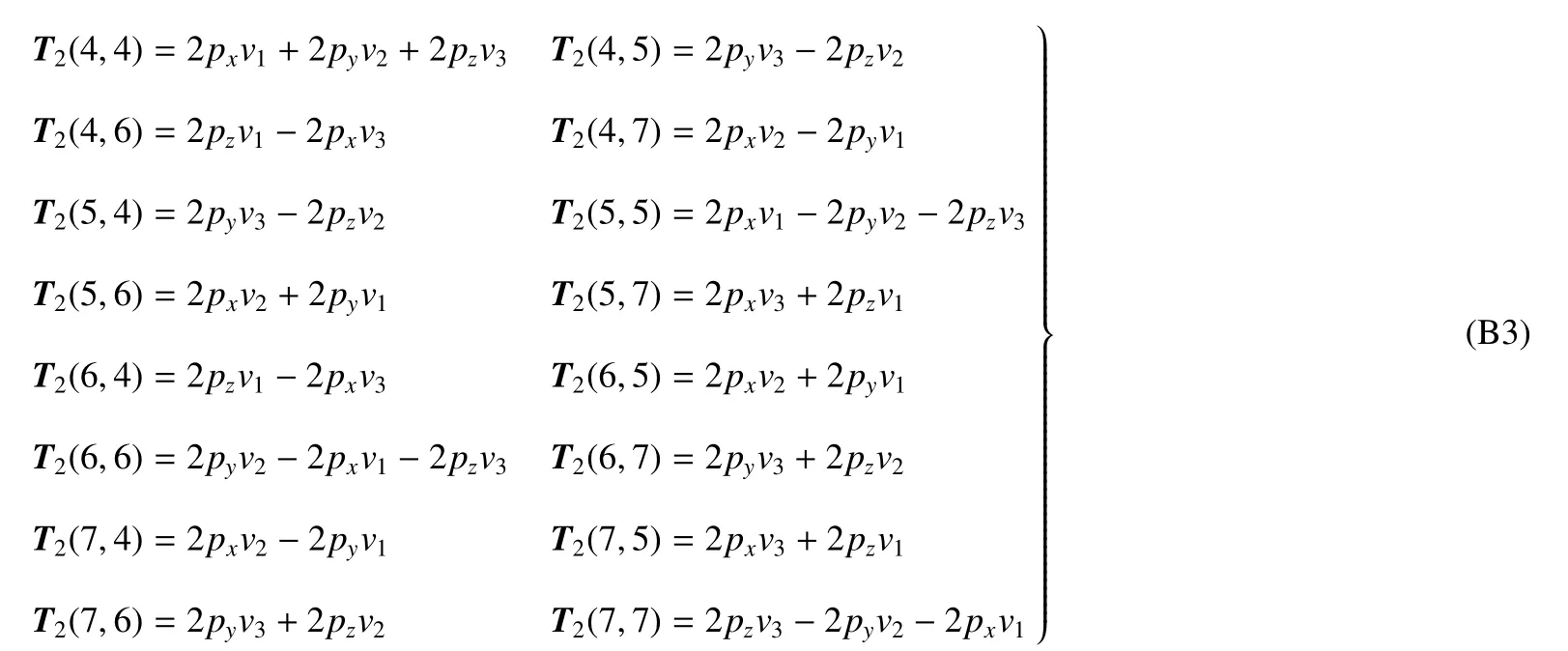考虑弹簧阻尼作动器解析雅可比矩阵的多刚体动力学分析1)

2017-11-11阚子云彭海军陈飙松

力学学报 2017年5期

关键词：阻尼弹簧动力学

阚子云彭海军陈飙松

(大连理工大学工程力学系工业装备结构分析国家重点实验室,辽宁大连116024)

考虑弹簧阻尼作动器解析雅可比矩阵的多刚体动力学分析1)

阚子云彭海军2)陈飙松

(大连理工大学工程力学系工业装备结构分析国家重点实验室,辽宁大连116024)

弹簧--阻尼--作动器(spring-damper-actuator，SDA)是多体系统中常见的力元，在工程领域中有着广泛的应用.采用绝对坐标方法建立的多体系统动力学控制方程通常是复杂的非线性微分--代数方程组.为了保证数值解的精度和稳定性，通常需要采用隐式算法求解动力学方程，而雅可比矩阵的计算在隐式数值求解过程中至关重要.对于含有SDA的多体系统，SDA造成的附加雅可比矩阵是与广义坐标和广义速度相关的高度非线性函数.目前的很多研究工作专注于广义力向量的计算，然而对附加雅克比矩阵的计算则少有关注.针对含SDA的多刚体系统进行动力学分析，首先基于Newmark算法研究其在动力学方程求解中的雅可比矩阵的构成形式;然后推导SDA的广义力向量对应的附加雅可比矩阵，其中包括广义力向量对广义坐标和对广义速度的偏导数矩阵.最后通过两个数值算例研究附加雅可比矩阵对动力学分析收敛性的影响;数值分析表明：当SDA的刚度、阻尼和作动力数值较大时，SDA导致的附加雅可比矩阵对数值解的收敛性有重要影响；当考虑SDA对应的附加雅可比矩阵时，动力学分析可以以较少的迭代步实现收敛，从而减少分析时间.

弹簧阻尼作动器，雅可比矩阵，多体系统，隐式算法，张拉整体结构

引言

对复杂机械系统进行动力学分析前需要建立其多体系统动力学模型，建模的实质是对系统中4个要素进行定义[1]：物体、铰、主动力、力元.其中力元反映了物体与物体间的相互作用.弹簧--阻尼--作动器(spring-damper-actuator，SDA)系统是多体系统中的常见力元,可以有效地模拟工程中机构或结构的某些元器件的静力和动力特性,在机械、汽车、土木等领域得到广泛的应用[26].

采用绝对坐标方法对多体系统进行动力学分析得到的控制方程通常是复杂的非线性微分--代数方程组.在数学上，微分方程的求解通常可分为显式算法和隐式算法两类.显式算法不需要迭代求解，算法稳定域较小，因此需要较小的时间步长才能满足长时间仿真的精度要求，通常不用于非线性程度较高且呈现刚性特点的多体系统[7]；而隐式算法采用迭代求解策略，在每一增量步内都需要对离散非线性平衡方程进行迭代求解，可以采用较大的时间步长同时满足解的精度和稳定性要求.另一方面，多体动力学方程中包含代数方程，其求解不同于一般的常微分方程组，根据约束方程的不同处理方式，又可以将微分--代数方程组的求解归纳为增广法和缩并法两大类.直接时间积分法是增广法中的一类重要求解算法，经典的有Newmark法[8]、HHT法[910]、广义α法[11]以及近年来出现的Bathe积分方法[1213]、祖冲之类保辛算法[1415]等.这些算法在数学上均属于隐式算法，在求解过程中同时对连续时间域的动力学控制方程(包含约束方程)进行离散，得到离散时间点处的非线性平衡方程，通过滚动求解非线性平衡方程来完成整个时间域的分析.在每一时间步的非线性平衡方程的迭代求解中，需要计算系统的雅可比矩阵，类似于非线性有限元领域的切线刚度阵或结构动力学中的等效刚度阵.SDA作为多体系统中的力元可以理解成系统中的内力源之一，影响着多体动力学方程中的广义力向量的集成，并对系统的总体雅可比矩阵产生贡献.对应SDA的雅可比矩阵则是与广义坐标以及广义速度相关的复杂非线性函数.而计算多体系统动力学领域中的多部经典专著[1,1619]在进行相关介绍时，一般专注于广义力向量的计算，而对SDA导致的附加雅可比矩阵的计算尚未见有完整系统的报道.雅可比矩阵的计算在多体动力学分析中至关重要，当不易解析地计算非线性方程的雅克比矩阵时，一般可以采用两种处理方法：一是采用数值差分[20]，计算出离散非线性平衡方程的近似雅可比矩阵，这种方式简单易行但对于大规模问题，效率十分低下；另一种折衷的办法是选取易于解析计算的部分项参与总体雅可比矩阵的组装.当系统中含有SDA时，则忽略SDA产生的附加雅克比矩阵.然而在多体动力学求解中不计入SDA造成的雅可比矩阵贡献时，会使系统的总体雅可比矩阵不精确，最终可能会导致非线性求解过程中收敛速度变慢，甚至完全不能收敛.

鉴于此，本文首先以多体动力学方程求解的Newmark算法为例，说明其雅可比矩阵的具体构成形式，以及 SDA对应的广义力向量.进一步推导了SDA在动力学分析中附加的雅可比矩阵的精确形式，包括广义力向量对广义坐标以及广义速度的偏导数矩阵.并在附录中以姿态角的四元数描述为例，给出了雅可比矩体组成关键项的具体表达式.当姿态角采用欧拉角或卡尔丹角等其他类型描述时，只需计算出其对应的关键项的表达式，进行整体代入即可.最后通过数值算例研究了SDA产生的附加雅可比矩阵对多体系统动力学分析收敛性的影响.

1 多体动力学方程及其数值求解

典型的多体系统动力学方程是如下形式的指标-3的微分代数方程组

其中M为系统的广义质量矩阵，Φ和Φq分别为系统的约束方程及约束雅可比矩阵，Qi,Qa和Qe分别为系统的耦合惯性力、外加力、内力.对于含有SDA的多体系统，其对系统总体广义力向量的影响体现在内力Qe中.此处以及后文中黑斜体表示矩阵或向量，斜体均表示标量.

以经典的Newmark算法为例，考察其雅可比矩阵组成.在时间区间[tn,tn+1]内，Newmark算法采用如下假设公式

式中∆t为时间步长，α和δ为Newmark参数，带顶标“～”的量为当前时间步的待求未知量.为了书写方便，将式(1)中第1项的等号右端项统称为总体广义力向量Qt.动力学方程离散后得到的系统的非线性代数方程组为

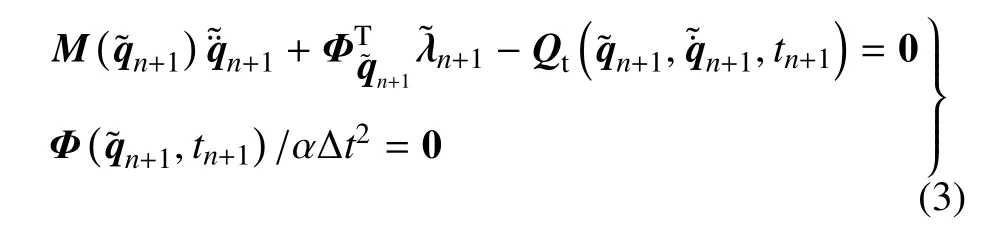
其中

当多体系统中含SDA时，其将对总体广义力向量Qt产生贡献，具体通过式(4)中 P3项具体影响雅可比矩阵J的构成.上述虽仅针对Newmark算法说明其雅可比矩阵的构成，对其他时间积分算法，雅可比矩阵的具体形式虽然略有不同，但是都不可避免地需要对矩阵∂Qe/∂q和进行计算.此外，在多体系统的静平衡分析中，当忽略速度和加速度相关项后，获取精确的雅可比矩阵仍需要计算∂Qe/∂q.

2 弹簧--阻尼--作动器系统的动力学模型

如图1所示,物体I和物体J通过SDA连接，连接点分别为Pi和Pj.当前时刻两物体相对于全局坐标系的位形坐标(广义坐标)为

广义速度

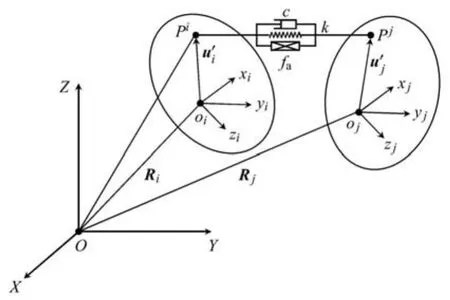
图1 SDA示意图Fig.1 Schematic diagram of SDA

式 (8)和式 (9)中 Ri∈ R3×1和 Rj∈ R3×1分别表示固结在物体 I和 J上的局部坐标系的原点相对于全局坐标系的矢量在全局坐标系的投影.Θi和Θj分别表示各自物体的局部坐标系相对于全局坐标系的姿态角.此种建模方式即为多体动力学中最为经典和工程中普遍使用的笛卡尔绝对建模方式.当采用欧拉角或卡尔丹角描述姿态角Θi∈R3×1,Θj∈R3×1，一个物体共有6个广义坐标.当采用四元数描述姿态角时，Θi∈ R4×1，Θj∈ R4×1，一个物体共有7个广义坐标.值得说明的是：由于四元数之间并非相互独立，此种情况下动力学方程中需要添加相应的约束方程.为统一起见，以下将单个物体对应的广义坐标个数记为N.

记Pi和Pj点在全局坐标系的坐标分别为RPi∈R3×1和 RPj∈ R3×1，则有

将式(14)对时间求导，根据数学关系知

令

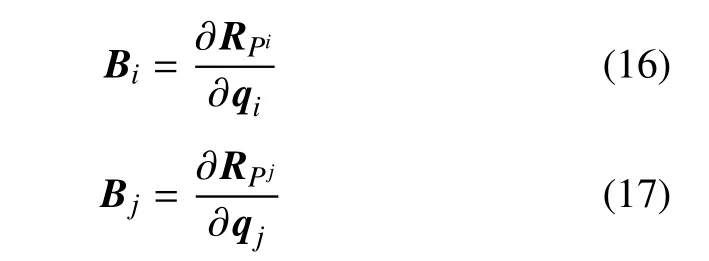
其中，Bi∈ R3×N,Bj∈ R3×N，根据刚体运动学的相关知识,Bi和Bj的表达式亦可以简洁写成如下形式

弹簧的当前长度为

定义沿矢量h方向的单位矢量为ˆh∈R3×1，其相对与全局坐标系中的投影为

弹簧当前长度的变化率为

设弹簧的刚度系数为k，阻尼器的阻尼系数为c，作动器的主动作用力为 fa.SDA的作用力始终沿Pi和Pj的连线，其大小为

物体I和J上所受到的作用力在全局坐标系下的列阵为

由式(16)和式(17)知

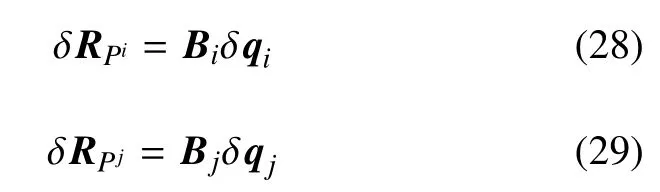
另一方面，SDA的广义力向量Qei∈RN×1和Qej∈RN×1与虚功有如下关系

将式(25)，式(26)，式(28)，式(29)代入式(27)并与式(30)比较可知，作用在物体I和物体J上的广义力向量为

和有限元分析中的节点力向量的组装类似，对于含有SDA的多体系统，在静平衡或动力学分析中，按上述公式计算其对应的广义外力阵，累加到全局广义坐标阵对应的位置.

3 弹簧--阻尼--作动器系统的雅可比矩阵

3.1 雅可比矩阵之一：∂Q/∂q

第2节给出了动力学方程中广义外力阵和广义坐标之间的关系，本节推导广义力向量对广义坐标的偏导数项.方便起见，根据广义坐标所属物体的不同，将此矩阵写成分块形式，即

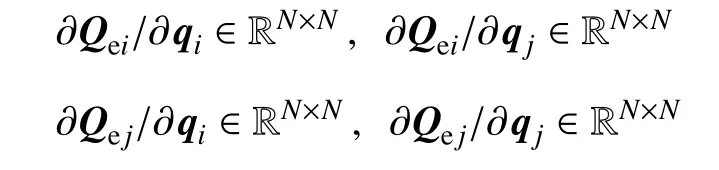
在总体雅可比矩阵中，∂Qei/∂qi和 ∂Qej/∂qj分布在主对角线附近，而 ∂Qei/∂qj和 ∂Qej/∂qi为耦合项，其分布在远离主对角线位置.为推导方便，首先进行以下中间量的计算

综合式(24)、式(33)～式(38)得

同理可得

结合式(31)和式(32)，对于主对角元项有

前述已经提及Bi的表达式和qj无关联，Bj和qi无关联.对于任意的V向量，V∈R3×1，有

故对于耦合项，有

综合式(39)～式(46)，即得SDA对应的广义力向量对广义坐标的偏导数矩阵.注意到在式(39)～式(42)中涉及到Bi和Bj(或其转置矩阵)与某一向量乘积后对广义坐标求导的矩阵，即

理论上这些项可以由矩阵Bi和Bj(每一个元素)对广义坐标qi，qj的偏导数构成的三维矩阵和待乘向量复合而成，或写成张量形式，但这样做并不利于程序的设计.附录中直接以四元数为例给出了其具体的表达式.对于其他形式的姿态描述方式，可直接根据Bi(Bj)矩阵的每一项经过简单求导得出.

3.2 雅可比矩阵之二：∂Q/∂˙q

当SDA中的阻尼器的阻尼不为0时，广义力向量和广义速度相关.本节给出广义力向量对广义速度的偏导数.在动力分析中，此项对于雅可比矩阵的精确计算，亦必不可少.注意到

故有

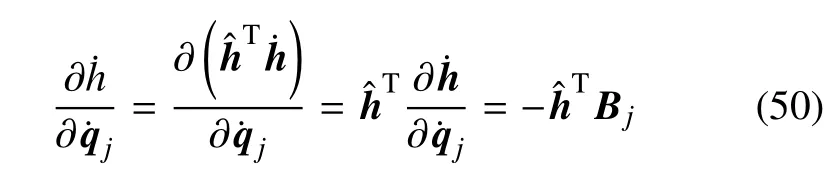
根据式(24)，有

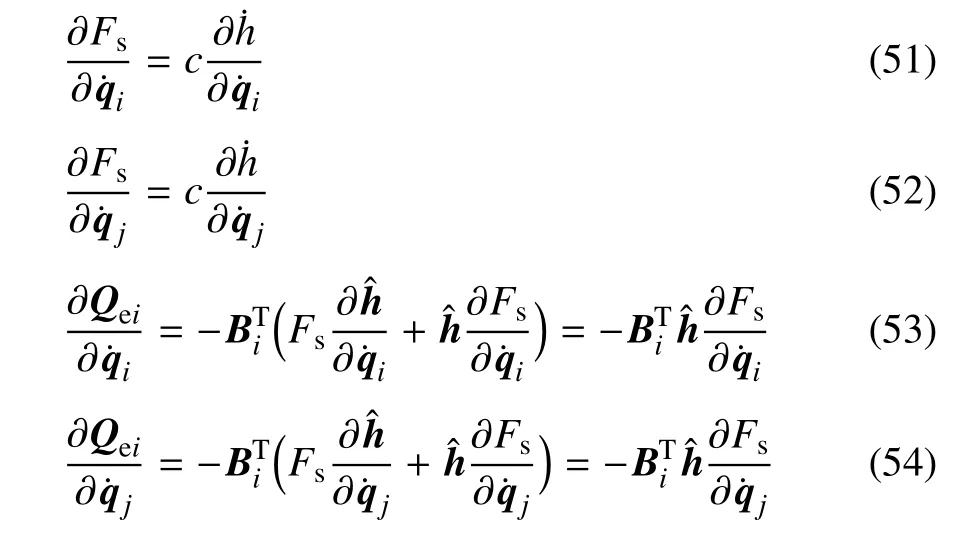
综合式(49)～式(54)有

同理

可以看出广义力向量对广义速度的偏导数相比于广义力向量对广义坐标的偏导数公式更为简洁，且当写成整体形式时，此矩阵具有对称性.

3.3 考虑雅可比矩阵的计算流程

3.1和3 .2节中给出的SDA对应附加的雅克比矩阵是完全精确的，未引入任何的近似.从相关公式可以看出其涉及到的计算量较大，且表达式复杂，呈现出高度的非线性.为了便于有序、高效地进行数值计算，下面给出了SDA对应的广义力向量和雅可比矩阵的计算流程：

(4)根据式(24)计算内力Fs,根据式(31),式(32)计算广义外力阵Qei,Qej.

(8)根据式(41),式(42),式(45),式(46)计算

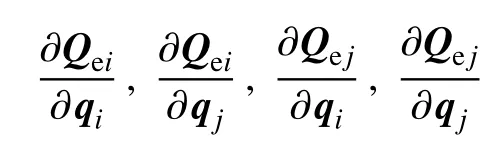
(9)根据式(55)～式(58),计算

4 数值算例

为了说明上述雅可比矩阵的有效性，本节针对两个算例，进行多体动力学计算，并着重从雅可比矩阵的构成对多体动力学分析的收敛性以及计算效率的角度进行分析.多体系统中物体的姿态均采用四元数进行描述，以避免欧拉角或卡尔丹角建模可能造成的奇异问题[1].程序的运行环境为MATLAB R2016a，处理器：Intel Core i5-4300U@1.90GHz、内存4GB.

4.1 曲柄滑块机构

如图2所示的曲柄滑块机构，1号连杆与地面，2号连杆与1号连杆，2号连杆与滑块3之间分别通过旋转铰连接，滑块3可沿地面水平滑动，其上作用大小为1kN，水平向右的力.连杆1和2的之间连接有SDA，连接点在分别在两连杆的质心处，SDA的刚度为 k(单位:N/m)，阻尼为 c(单位:N·s/m)，作动力为 fa(单位:N).连杆1和连杆2杆长均为2m，质量均为50kg，垂直于杆长方向的转动惯量均为15 kg·m2，沿杆长方向的转动惯量均为 0.02kg·m2.滑块的质量为1kg，绕惯性主轴方向的转动惯量均为1kg·m2，不计重力，无初始速度.

图2 曲柄滑块机构Fig.2 Slider-crank mechanism

采用Newmark算法对上述算例进行动力学分析.时间步长取∆t=0.01s，仿真步数：100.Newmark参数取α=0.25，δ=0.5，在此种参数选择下Newmark算法为二阶精度且无能量耗散.每一时间步的非线性代数方程组采用牛顿--拉夫逊迭代算法计算，初始迭代值取为上一时间步末端的广义加速度和拉氏乘子向量，收敛误差按残差的2范数定义，取ε=1×10−7.

图3～图5分别给出了在参数c=0，fa=0下变化弹簧刚度k、不计入和计入SDA的雅可比矩阵对应的收敛曲线、以及两种情况下的分析时间对比.可以看出，当不计入SDA造成的附加雅可比矩阵项时，每一时间步需要的收敛步数随着刚度k的增加而增加.相比之下，计入SDA造成的附加雅可比矩阵可以保证每一时间步更快的收敛，在当前情况，各时间步的非线性方程组求解均只需要3步即可收敛到指定精度.

图3 不计SDA的雅可比矩阵，每一时间步的迭代步数Fig.3 Iteration number of each time step excluding the Jacobian matrix of SDA

图4 计入SDA的雅可比矩阵，每一时间步的迭代步数Fig.4 Iteration number of each time step including the Jacobian matrix of SDA

图5 分析时间对比Fig.5 Comparison of analysis time

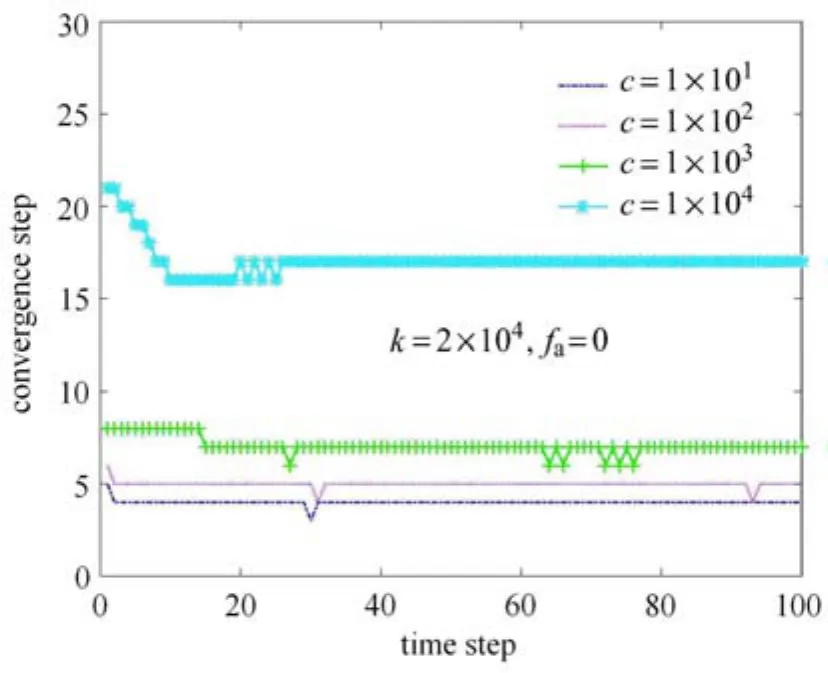
图6 不计SDA的雅可比矩阵，每一时间步的迭代步数Fig.6 Iteration number of each time step excluding the Jacobian matrix of SDA

上述结果只考虑了SDA的参数c=0的情况.根据式(55)～式(58)，此种情况下SDA的广义力向量对广义速度的偏导数为零矩阵，相当于只考察了SDA的广义力向量对广义坐标的偏导数对收敛性的影响.为了考察广义力向量对广义速度的偏导数对收敛性的影响，选取固定的k=2×104，fa=0，c分别取 1×101，1×102，1×103，1×104等4种情况进行动力学计算.分别考虑在总体雅克比矩阵中不计和计入SDA的广义力向量对广义速度的偏导数对雅可比矩阵的附加项的情况.每一时间步的迭代步数和分析时间如图6～图8所示.从图6可以发现当不计入此附加修正项时，每一时间步需要的收敛步数随着c的增加而增加.由图7和图8可知计入本文推导的精确雅克比修正项后，所需迭代步更少，节省计算时间，特别是对于SDA的阻尼较高的情况.采用控制变量法对作动器的作动力fa进行分析，可以得到类似的结论.另外当尝试进行静平衡分析时，不计入总体雅可比矩阵中SDA对应的部分，则完全不能收敛.

图7 计入SDA的雅可比矩阵，每一时间步的迭代步数Fig.7 Iteration number of each time step including the Jacobian matrix of SDA

图8 分析时间对比Fig.8 Comparison of analysis time

4.2 Tensegrity的找形分析

Tensegrity是由多个不连续的压杆和连续的拉索构成的空间机构，最早来自于艺术领域，后被应用到航空航天、建筑结构等工程领域[2324].找形分析[2530]是Tensegrity设计过程中的重要环节.本算例来自文献[31]，考察初始位形如图9所示的由6根压杆，21根拉索的两层Tensegrity结构，粗线表示压杆，细线表示拉索.采用多体动力学方法，将压杆考虑为物体，拉索由SDA模拟.借鉴动力松弛法[3233]的思想，在初始的不平衡力的作用下构件发生运动，SDA的阻尼器耗散能量最终使系统趋于平衡状态，从而完成找形分析.压杆的质量均为0.3kg，垂直于杆长方向的转动惯量均为0.1kg·m2，沿杆长方向的转动惯量均为0.01kg·m2.拉索的原始长度和连接信息详见文献[31].

图9 系统的初始位形Fig.9 Initial position of the system

通过此算例考察，当系统中含有多个SDA时，雅可比矩阵对收敛的影响，不考虑作动器的作用，即fa=0.所有弹簧的刚度k(单位:N/m)，以及阻尼c(单位:N·s/m)保持一致，无初始速度.不对系统做外在约束，以体现Tensegrity结构“自平衡”的特点.Newmark参数取α=0.3，δ=0.6，步长取∆t=0.01s，收敛误差取ε=1×10−7，每一时间步的最大迭代步数设为1000.将SDA对应的∂Qe/∂q和项分别简记为M2和M3，精确雅可比矩阵的其他部分记为M1.

表1给出了在若干SDA参数下，选取不同的部分参与雅可比矩阵组装，仿真前100步的平均收敛步数和和计算时间.从中可以看出动力学分析的收敛情况与参数的选取有着紧密的关系.对于此算例，采用完全精确的雅可比矩阵相比于只考虑部分项的雅可比矩阵，每一步所需要的迭代步更少.对于弹簧刚度k较小，阻尼c较大的情况，M3项对收敛速度的影响较大.当弹簧的刚度k较大时，各种情况的收敛性均变差.对于第8种参数，甚至完全精确的雅可比矩阵也不收敛，这是因为，此种情况下弹簧的刚度大且无阻尼，在较短的时间内，系统的位形变化大，当前的时程分析步长∆t=0.01s取得过大.对于第5种参数可以观察到似乎反常的情况，只计入M1项和计入M1+M2或M1+M3项相比，平均迭代步变多而总体分析时间却变少，这是因为计算SDA的雅可比矩阵需要耗费一定的时间，迭代步减少所节省的时间并不一定能够以抵消矩阵计算所带来的额外开销，但是对完全精确的雅可比矩阵(M1+M2+M3)相比于只计入M1项在收敛速度和时间上仍有明显的优势.对于含有较多的SDA的多体系统，精确计算其造成的雅可比矩阵是必要的.

表1 不同参数下的平均迭代步数与计算时间对比Table 1 The average iteration number and computing time by di ff erent parameters

图10给出了弹簧刚度k=200N/m，阻尼系数c=10N·s/m时，系统在0～0.3s区间的能量变化曲线，其中残余能量定义为：物体的总动能+SDA的总弹性势能，SDA耗散的能量即为阻尼器做的功，算法耗散的能量定义为：系统的初始能量–残余能量–SDA耗散的能量.首先可以发现系统的残余能量迅速被耗散到较低的水平并缓慢衰减,这说明系统在较短的时间内即运动到平衡状态附近.此外可以观察到Newmark算法自身耗散能量远小于SDA阻尼器做的功.随着仿真时间的增加，各能量将趋于稳定.图11给出了在上述参数选取下，仿真至20s后的结果，以及文献[31]的结果，可以看出，二者在形态上比较一致，从而侧面说明了此算例分析的正确性.进一步的分析表明，在平衡构型下，杆件全部处于受压状态，绳索均处于受拉状态，其中上层的3根侧边绳索所受的拉力最大，约为4.92N，说明此算例构造的合理性.

图10 系统的能量变化曲线Fig.10 System energy variation curve

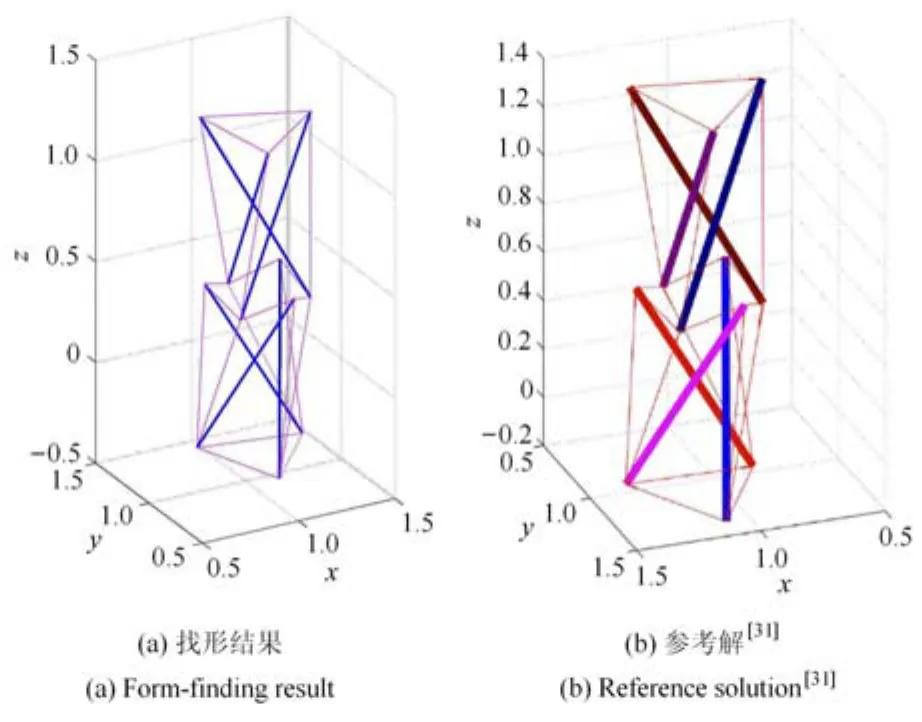
图11 找形的结果对比Fig.11 Comparison of the form- fi nding result

5 结论

采用隐式算法对多体系统动力学微分--代数方程求解，需要计算系统的雅可比矩阵.对于含有SDA的多体系统，其造成的雅可比矩阵是广义坐标的复杂非线性函数.本文以多体动力学微分-代数方程的Newmark求解算法为例，说明其雅可比矩阵的构成形式，以及SDA对雅可比矩阵的具体的影响项.详细推导了多体系统动力学中SDA的精确的雅可比矩阵，包括广义力向量对广义坐标的偏导数矩阵和广义力向量对广义速度的偏导数矩阵.以姿态角的四元数描述为例，给出了其组成关键项的具体表达式.当姿态角采用欧拉角或卡尔丹角等其他类型描述时，只需计算出其对应的关键项的表达式，进行整体代入即可.在此基础上，进一步研究了SDA引起的雅可比矩阵对动力学分析收敛性的影响，结果表明随着SDA的弹簧刚度，阻尼器的阻尼以及作动器的作用力的增大，SDA造成的附加雅可比矩阵对多体动力学分析收敛性影响明显.采用不考虑SDA造成的附加雅可比矩阵会动力学分析导致收敛速度变慢，甚至不能收敛.利用本文推导的公式，计入SDA影响的精确的雅可比矩阵无论是从迭代步数还是从最终的仿真时间上来看，都能够达到很好的分析效果.本文中考虑的SDA为线性弹簧和线性阻尼器，且SDA的连接物体均为刚体的情况，对于非线性弹簧或非线性阻尼器的SDA或SDA关联物体为柔性体的情况可按照类似的思路导出.

1洪嘉振.计算多体系统动力学.北京:高等教育出版社,1999(Hong Jiazhen,Computational Dynamics of Multibody Systems.Beijing:Higher Education Press,1999(in Chinese))

2石奇端,马履中.六自由度并联机构组合弹簧阻尼减振装置.农业机械学报,2007,38(8):128-131(Shi Qiduan,Ma Luzhong.Research on the device of 6-dof parallel mechanisms combined with elastic damping system.Transactions of the Chinese Society for Agricultural Machinery,2007,38(8):128-131(in Chinese))

3王其东,陈无畏,张炳力.基于多体模型的汽车半主动悬架控制方法研究.机械工程学报,2004,40(1):104-108(Wang Qidong,Chen Wuwei,Zhang Bingli.Study on the control method of automobile semi-active suspension based on the multibody model.Journal of Mechanical Engineering,2004,40(1):104-108(in Chinese))

4刘颖,王瑞.基于计算多体系统动力学的机织卡尔丹角多体动力学模型.机械工程学报,2014,50(5):102-107(Liu Ying,Wang Rui.A cardan angular model of rigid bodies for woven fabrics based on the dynamics of multibody systems.Journal of Mechanical Engineering,2014,50(5):102-107(in Chinese))

5谭蔚，贾占斌，聂清德.弹簧阻尼器在塔器防振中的应用.化学工程,2013,41(12):16-19,34(Tan Wei,Jia Zhanbin,Nie Qingde.Application of spring damper in antivibration of columns.Chemical Engineering,2013,41(12):16-19,34(in Chinese))

6王庚祥，刘宏昭.多体系统动力学中关节效应模型的研究进展.力学学报，2015,47(1):31-50(Wang Gengxiang,Liu Hongzhao.Research progress of joint e ff ects model in multibody system dynamics.Chinese Journal of Theoretical and Applied Mechanics,2015,47(1):31-50(in Chinese))

7王国平.多体系统动力学数值解法.计算机仿真,2006,23(12):86-89(Wang Guoping.Numerical algorithms of multibody system dynamics.Computer Simulation,2006,23(12):86-89(in Chinese))

8 Newmark N.A method of computation for structural dynamics.ASCE Journal of the Engineering Mechanics Division,1959,85:67-94

9 Negrut D,Rampalli R,Ottarsson G,et al.On an implementation of the Hilber-Hughes-Taylor method in the context of index 3 di ff erential-algebraic equations of multibody dynamics.Journal of Computational and Nonlinear Dynamics,2007,2(1):73-85

10马秀腾，翟彦博，谢守勇.多体系统指标2运动方程HHT方法违约校正.力学学报,2017,49(1):175-181(Ma Xiuteng,Zhai Yanbo,Xie Shouyong.HHT method with constraints violation correction in theindex2equationsofmotionformultibodysystem.ChineseJournal of Theoretical and Applied Mechanics,2017,49(1):175-181(in Chinese))

11 Chun J,Hulbert G.A time integration algorithm for structural dynamics with improved numerical dissipation:the generalized-α method.ASME Journal of Applied Mechanics,1993,60(2):371-375

12 Bathe KJ,Baig MMI.On a composite implicit time integration procedure for nonlinear dynamics.Computers and Structures,2005,83(31-32):2513-2524

13 Bathe KJ.Conserving energy and momentum in nonlinear dynamics:A simple implicit time integration scheme.Computers and Structures,2007,85(7-8):437-445

14钟万勰,高强.约束动力系统的分析结构力学积分．动力学与控制,2006,4(3):193-200(Zhong Wanxie,Gao Qiang.Integration of constrained dynamical system via analytical structural mechanics.JournalofDynamicsandControl,2006,4(3):193-200(inChinese))

15吴锋,高强,钟万勰.基于祖冲之类方法的多体动力学方程保能量保约束积分.计算机辅助工程,2014,23(1):64-68(Wu Feng,Gao Qiang,Zhong Wanxie.Energy and constraint preservation integration for multibody equations based on Zu Chongzhi method.Computer Aided Engineering,2014,23(1):64-68(in Chinese))

16 Shabana AA.Dynamics of Multibody Systems(3rd edition).New York:Cambridge University Press,2005

17 Bayo E,Garc´ıa de Jal´o J.Kinematics and Dynamics Simulation of Multibody System,the Real-time Challenge.New York:Springer,1994

18张雄,王天舒.计算动力学.北京:清华大学出版社,2007(Zhang Xiong,Wang Tianshu.Computational Dynamics.Beijing:Tsinghua University Press,2007(in Chinese))

19刘延柱,潘振宽,戈新生.多体系统动力学(第2版).北京:高等教育出版社,2014(LiuYanzhu,PanZhenkuan,GeXinsheng.Dynamics of Multibody Systems(2nd edition).Beijing:Higher Education Press,2014(in Chinese))

20 Hussein BA,Shabana AA.Sparse matrix implicit numerical integration of the sti ffdi ff erential/algebraic equations:implementation.Nonlinear Dynamics,2011,65:369-382

21田强.基于绝对节点坐标方法的柔性多体系统动力学研究与应用.[博士论文].武汉:华中科技大学，2009(Tian Qiang.Research and application of fl exible multibody system dynamics based on the absolute nodal coordinate method.[PhD Thesis].Wuhan:HuazhongUniversityofScienceandTechnology,2009(inChinese))

22 Bottasso CL,Dopico D,Trainelli L.On the optimal scaling of index three DAEs in multibody dynamics.Multibody System Dynamics,2007,19:3-20

23 Motro R.Tensegrity systems:the state of the art.International Journal of Space Structures,1992,7:75-82

24 Skelton R,de Oliveka M.Tensegrity Systems. New York：Springer，2009

25 Pagitz M,Mirats Tur JM.Finite element based form- fi nding algorithm for tensegrity structures.International Journal of Solids and Structures,2009,46:3235-3240

26 Gasparini D,Klinka KK,Arcaro VF.A fi nite element for formfi nding and static analysis of tensegrity structures.Journal of Mechanics of Materials&Structures,2011,6(9-10):1239-1254

27 Koohestani K.Form- fi nding of tensegrity structures via genetic algorithm.International Journal of Solids and Structures,2012,49:739-747

28 Tran HC,Lee J.Form- fi nding of tensegrity structures using double singular value decomposition.Engineering with Computers,2013,29:71-86

29 Koohestani K,Guest S.A new approach to the analytical and numerical form fi nding of tensegrity structures.International Journal of Solids and Structures,2013,50(19):2995-3007

30 Zhang LY,Li Y,Cao YP,et al.Sti ff ness matrix based form- fi nding method of tensegrity structures.Engineering Structures,2014,58:36-48

31 Massimo C,Josep M,Mirats T.A comprehensive dynamic model for class-1 tensegrity systems based on quaternions.International Journal of Solids and Structures,2011,48:785-802

32 Barnes MR.Form fi nding and analysis of tension structures by dynamic relaxation.International Journal of Space Structures,1999,14(2):89-104

33 Ali NBH,Rhode-Barbarigos L,Smith IFC.Analysis of clustered tensegrity structures using a modi fi ed dynamic relaxation algorithm.InternationalJournalofSolidsandStructures,2011,48(5):637-647

RIGID BODY SYSTEM DYNAMIC WITH THE ACCURATE JACOBIAN MATRIX OF SPRING-DAMPER-ACTUATOR1)

Kan Ziyun Peng Haijun2)Chen Biaoshong
(State Key Laboratory of Structural Analysis for Industrial Equipment，Department of Engineering Mechanics，Dalian University of Technology，Dalian 116024，China)

The spring-damper-actuator(SDA)is a common force element in multibody system and widely used in the fi eld of engineering.The governing equations of multibody dynamic system established by absolute coordinate methods are di ff erential-algebraic equations which are usually nonlinear and complex.To ensure the stability and accuracy of the numerical solutions,the implicit algorithms are commonly used to solve the dynamic equations.While the calculations of Jacobian matrices are the crucial process in implicit algorithms.For a multibody system containing the SDA,the additional Jacobian matrices induced by the SDA are highly nonlinear functions of the generalized coordinates and generalized velocities.A lot of current research works focus on the calculation of generalized force vector,however the calculations of additional Jacobian matrices are less concerned.This paper focuses on dynamic analysis of multi-rigid-body systems containing the SDA.Firstly,the construction of the accurate Jacobian matrices in solving the dynamic equations is investigated based on the Newmark algorithm.Then,the additional Jacobian matrices relating to the generalized force vector of the SDA are analytically derived.These matrices consist of the partial derivative of generalized force vector with respect to the generalized coordinates and the generalized velocities.Finally,the in fl uence of additional Jacobian matrices on the convergence of dynamic analysis is investigated via two numerical examples.The numerical results indicate that when the values of sti ff ness,damping and active force are large,the additional Jacobian matrices induced by the SDA have a signi fi cant in fl uence on the convergence of dynamic analysis.When the additional Jacobian matrices induced by the SDA are taken into account,the dynamic analysis can achieve convergence with less iteration steps and the computational time thus can be reduced.

spring-damper-actuator,Jacobian matrix,multibody systems,implicit algorithm,tensegrity

O313.7

10.6052/0459-1879-17-030

2017–01–23收稿，2017–05–23 录用,2017–05–24 网络版发表.

1)国家自然科学基金(11472069,11772074,91648204)和国家重点研发计划(2016YFB0200702)资助项目.

2)彭海军，副教授，主要研究方向:动力学与控制.E-mail:hjpeng@dlut.edu.cn

阚子云，彭海军，陈飙松.考虑弹簧阻尼作动器解析雅可比矩阵的多刚体动力学分析.力学学报，2017,49(5):1103-1114

Kan Ziyun,Peng Haijun,Chen Biaoshong.Rigid body system dynamic with the accurate Jacobian matrix of spring-damper-actuator.Chinese Journal of Theoretical and Applied Mechanics,2017,49(5):1103-1114

附录A 本文中约定的矩阵的求导运算法则