基于LQRI方法的蓄电池充电调节器控制策略

张泰峰，鲁 伟，邵兰娟，赵秋山

(中国电子科技集团公司第十八研究所，天津300384)

基于LQRI方法的蓄电池充电调节器控制策略

张泰峰，鲁 伟，邵兰娟，赵秋山

(中国电子科技集团公司第十八研究所，天津300384)

为提高卫星电源蓄电池充电调节器(BCR)的工作性能，基于带积分环节的线性二次型调节器(LQRI)设计方法提出了一种新型的BCR控制策略。根据BCR的工作机理，获得了系统的小信号数学模型；通过引入状态积分环节，实现了状态方程的扩维；通过定义二次型性能指标函数和加权矩阵，获得了一种新型BCR状态反馈控制策略，有效消除了系统的稳态输出误差。仿真结果验证了所提控制策略的有效性。

蓄电池充电调节器；线性二次型调节器；卫星电源；状态反馈

电源控制器(PCU)是卫星电源系统的关键组成单元，承担着卫星在轨期间电能的传输、转换和控制任务，动态调节发电单元、储能单元和负载之间的能量平衡。PCU的性能指标直接关系着卫星电源系统的品质。全调节母线PCU能够保证一次母线电压始终稳定在恒定值，在国内外各类卫星平台中得到了广泛的应用[1]。

蓄电池充电调节器(BCR)是全调节母线PCU的重要组成部分，负责在光照期对蓄电池组进行充电，保证蓄电池组的能量平衡。常见的BCR拓扑电路主要有Buck[2-4]、Superbuck[5-6]、SMART等。Buck电路由于结构简单、效率较高、输出电流脉动较小，是BCR设计的首选方案。

目前针对Buck电路的研究较多，但结合卫星电源系统特点，对基于Buck电路的BCR研究较少。含有积分控制的线性二次型最优控制算法(LQRI)具有静动态性能优越、易于工程化实现等诸多优点，已成功应用于风力发电[7]、电气化铁路[8]等领域，但LQRI方法在BCR系统中的应用还较少见。

本文针对Buck型BCR电路模型，通过引入状态积分环节，建立了扩维的小信号状态方程，并基于LQRI反馈控制器设计方法，提出了一种新型的BCR控制策略，仿真结果验证了该控制策略的有效性。

1 BCR数学模型

基于Buck拓扑的BCR电路如图1所示。其中，ISA表示太阳电池阵的输出电流；iCbus和iLoad分别为流入母线电容Cbus和负载RLoad的电流；vbus为母线电压；iBCR和iC分别为BCR的前端和后端电流；vbat为电池电压；QC、DC和LC分别为BCR电路的开关管、二极管和输出电感。

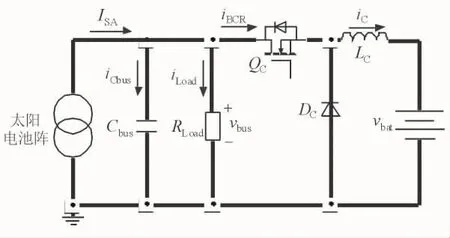
图1 BCR电路图

令变量d为开关管QC的占空比，由开关周期平均建模方法和基尔霍夫电压电流定理可得BCR电路的周期平均模型[4]：

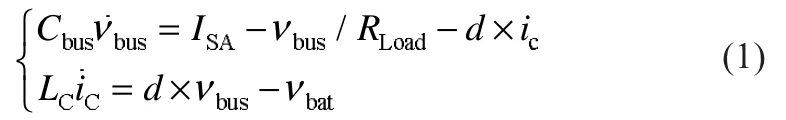
根据电路工作特性，定义变量vbus、iC和d的稳态值分别为Vbus、IC和D，易知系统稳态值分别为：

通过分析可知，针对式(2)所示的系统模型，采用传统的线性二次型调节器设计方法获得的控制率虽然可使系统具有较好的动态性能，但存在稳态输出误差无法消除的问题。因此本文采用LQRI方法，通过引入状态积分环节对状态方程进行扩维，使系统同时具有良好的动态和稳态性能。扩维后的系统小信号数学模型为：

根据系统特点，定义系统输出方程为：

2 BCR状态反馈控制策略

根据扩维后的BCR系统小信号数学模型，选取如下二次型性能指标J作为系统的目标函数：

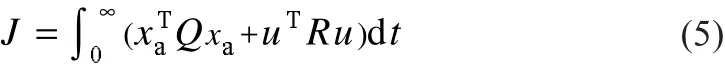
式中：正定对角阵Q和R分别为状态向量的加权矩阵和输入向量的加权矩阵。

由最优控制理论系统设计系统的最优反馈控制率为：

最优反馈增益矩阵K的表达式为：

矩阵P可通过求解如下Riccati方程获得：

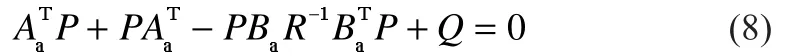
一般来说，加权矩阵Q和R的设计应充分考虑控制的需求，对于要求严格的变量，可以加大对应的权值，而对于要求较宽松的变量，其对应的权值可适当减小。

基于如上分析，可得基于LQRI方法的BCR状态反馈控制框图，如图2所示。

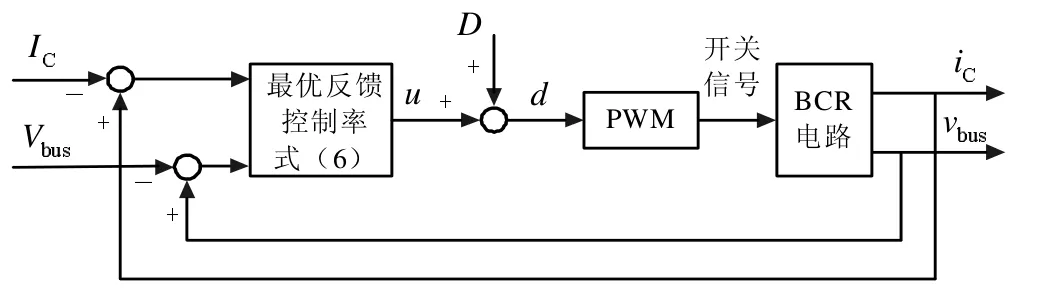
图2 BCR状态反馈控制框图

3 仿真实验研究

基于Matlab/Simulink软件环境，设计了针对图1所示的BCR仿真实验。选取的系统关键参数如表1所示，状态向量的加权矩阵Q和R分别为diag{1 000,10,1 000,10}、100。

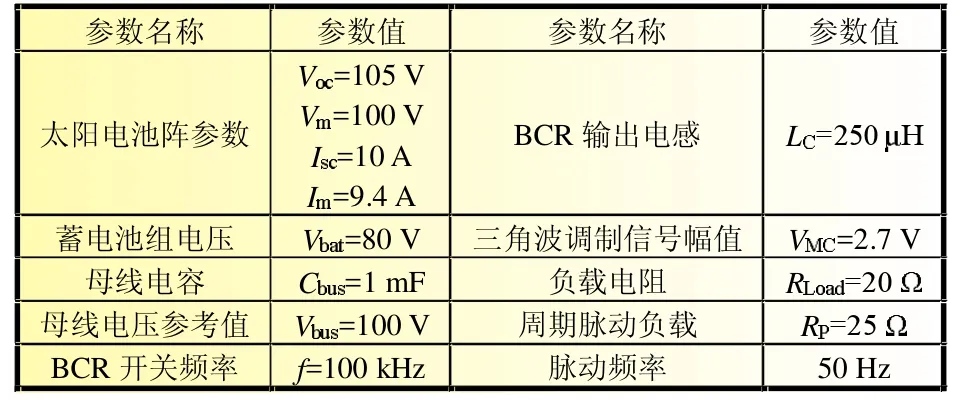
表1 BCR仿真系统关键参数

为验证本文所提控制策略的有效性，分别对系统的稳态工况和动态工况进行了仿真。当系统负载为固定电阻RLoad=20 Ω时，进入稳态后，负载电流iLoad、母线电压vbus和BCR后端电流(即蓄电池充电电流)iC波形如图3所示。由仿真结果可

图3 BCR稳态工况波形图

知，此时母线电压稳定在100 V，电压纹波峰峰值为4 mV，BCR后端电流稳定在5.35 A，电流纹波峰峰值为0.2 A。

为进一步验证系统对负载变化的动态响应能力和鲁棒性，在固定电阻RLoad基础上增加了频率50 Hz的周期脉动负载RP，基于所提控制策略的BCR动态响应波形如图4所示。由仿真结果可知，母线电压在负载变化时出现轻微超调现象，经0.6 ms母线电压即迅速稳定在100 V，最大超调幅值约为100 mV。BCR后端电流在负载变化时，经0.15 ms即可重新进入稳态，最大超调幅值约为0.7 A。动态工况下，系统响应快速，未出现不稳定震荡现象，这说明本文所提控制策略具有良好的动态特性和抗扰能力。

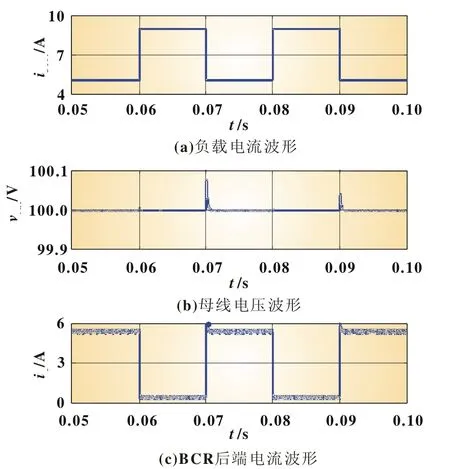
图4 BCR动态工况波形图

4 结论

针对BCR系统模型，本文基于LQRI方法提出了一种新型的状态反馈控制策略，不仅保证了BCR母线电压的稳定，而且对负载变化具有较强的鲁棒性，仿真结果验证了系统的良好性能。本文所提控制策略理论清晰、结构简单、易于工程化实现。本文的研究不仅为BCR的设计提供了新思想，而且具有较强的应用价值。

[1]赵春阳，陈洪涛.100 V母线10 kW级电源控制装置发展初探[J].电源技术，2008，32(9)：628-630.

[2]刘树林，刘健，寇蕾，等.Buck DC/DC变换器的输出纹波电压分析及其应用[J].电工技术学报，2007，22(2)：91-97.

[3]JARI L,TEUVO S.Characterizing the dynamics of the peak-currentmode-controlled Buck-power-stage converter in photovoltaic applications[J].IEEE Transactions on Power Electronics,2014,29(7):3840-3847.

[4]鲁伟，张泰峰，赵秋山，等.蓄电池充电调节器的稳健性设计分析[J].通信卫星工程，2016，2(2)：81-88.

[5]VAN D E,KLAASSENS J B,SPRUIJT H J N,et al.Battery charger design for the Columbus MTFF power system[J].IEEE Transactions on Aerospace and Electronic Systems,1997,33(1):29-37.

[6]PENGYU J,TRILLION-QIONG Z,YAN L.Parameter design of damping networks for the superbuck converter[J].IEEE Transactions on Power Electronics,2013,28(8):3845-3859.

[7]HEE-SANG K,JURI J,GUY D,et al.An advanced LMI-based-LQR design for voltage control of grid-connected wind farm[J].Electric Power Systems Research,2008,78:539-546.

[8]HU S J,ZHANG Z W,LI Y,et al.A new half-bridge winding compensation-based power conditioning system for electric railway with LQRI[J].IEEE Transactions on Power Electronics,2014,29(10):5242-5256.

Control strategy based on LQRI technique for battery charging regulation

ZHANG Tai-feng,LU Wei,SHAO Lan-juan,ZHAO Qiu-shan
(Tianjin Institute of Power Sources,Tianjin 300384,China)

To improve the performance of the battery charge regulator(BCR)of satellite power systems,a novel BCR control strategy was proposed using the method of linear quadratic regulator with integral action (LQRI).Based on the BCR working principle,the small-signal mathematic model was obtained.Then,the system state equation was dimensionally extended by adding two integrals of the state variables. Finally, the linear quadratic performance criterion and the weighting matrix were defined,and a novel state feedback control strategy of the BCR was obtained,which could effectively cancel the system steady-state errors.The effectiveness of the proposed control strategy was verified by simulation results.

battery charge regulator;linear quadratic regulator;satellite power system;state feedback

TM 91

A

1002-087 X(2017)10-1475-02

2017-03-15

张泰峰(1981—)，男，河南省人，博士，主要研究方向为空间电源技术。