平面问题中主应变测量不确定度评定

朱学旺，张思箭，刘青林，农绍宁



平面问题中主应变测量不确定度评定

朱学旺，张思箭，刘青林，农绍宁

（中国工程物理研究院 总体工程研究所，四川 绵阳 621999）

实现平面场中主应变的测量不确定度评定。首先建立主应变的是非线性传播测量模型，然后应用基于二阶TAYLOR级数展开理论的不确定度传播方法（LPU方法），开展平面问题中主应变的测量不确定度评定。针对二种常用的应变花，建立以主应变为输出量、以应变花之三个方向测量应变为输入量的测量模型，并将二阶LPU方法应用于该模型。设计数值计算算例，以说明主应变不确定度的评定过程和方法，并与一阶LPU结果进行了比较。当应变花三个方向的应变测量结果相近时，文中方法与一阶LPU方法获得的主应变的不确定度评定结果存在明显的差异，主应变不确定度评定结果在数值上都大于应变花测量的不确定度。当应变花三个方向的应变测量结果相差较大时，文中方法和一阶LPU方法获得的主应变测量不确定度评定结果相差不大。特定情况下，主应变的测量不确定度值远大于应变花测量的不确定度，且与一阶LPU方法的评定结果有显著差异，二者可相差一倍。

主应变；测量不确定度；二阶LPU方法；应变花；应变状态理论

当主应变作为实验应变测量的结果提供时，应该同时提供其测量不确定度，这是GUM（Guide to the Expression of Uncertainty in Measurement[1]），GJB 3756—1999[2]和 JJF 1059—1999[3]的通用要求。一般情况下，主应变并不能直接测量获得，除非主应变方向事先已知。工程中，应变花常用于结构表面任意一点的主应变测量，此时，利用应变花直接测量获得该点在三个方向的应变，应用应变状态空间理论计算得出该点的应变状态，进而得出该点的主应变。因此，主应变的测量不确定度评定是不确定度的传播分析的一种应用，其测量模型为主应变的计算公式，测量模型的输入是应变花三个方向的应变测量量。

针对应变的直接测量，其不确定度评定已有很多研究结论公布。简单地，应变测量的不确定度影响因素源自应变片的不确定度[4—5]和应变测量系统的不确定度[6—7]。按照标准推荐的方法，不难合成这两个因素的影响而获得应变花每个方向应变测量的不确定度。

尽管主应变测量模型会依据应变花的不同结构型式而具有不同的数学公式，但是他们具有一个共同特点：主应变的计算公式都是关于应变花各个方向应变测量量的非线性函数。这样，主应变的不确定度传递分析便不能直接应用GUM，GJB 3756和 JJF 1059等推荐的LPU方法，因为该方法仅适用于测量模型为线性或近似线性的导出测量量的不确定度传递分析。

对于非线性测量模型的导出测量量的不确定度分析，一般可以采用以下三种方法之一，即解析法、MC方法和高阶LPU方法[8]。文中尝试应用二阶LPU方法对平面问题中的主应变测量不确定度进行评定分析，主应变由应变花测量获得的应变直接测量量导出，而应变直接测量量的不确定度作为已知量处理。首先回顾了平面问题的主应变测量模型，给出了两种不同型式的应变花测量时的主应变计算公式。其次，介绍了基于二级Taylor级数展开理论的LPU方法（简称二阶LPU方法），并将其应用与直角型应变花和三角形应变花测量平面应变时的主应变分析模型。然后设计数值计算算例，说明文中方法的应用并比较主应变和应变花直接测量应变的不确定度评定结果以及一阶LPU方法的不确定度评定结果。

1 平面问题中主应变测量模型

根据应变状态理论，无论是平面应力状态还是平面应变状态，结构外表面上任意一点的任意方向的正应变（线应变）都可以采用规定坐标系下该点的应变状态参数ε，ε，γ来描述[9-10]：

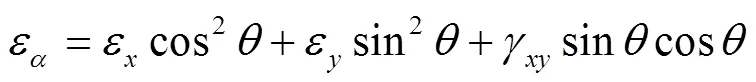
应用三角公式，式（1）还可以写成：

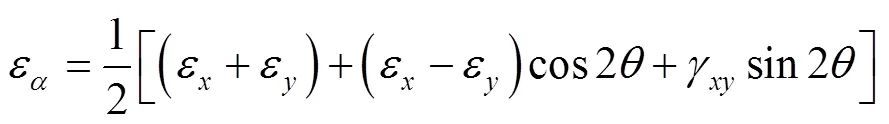
从式（1）或（2）不难发现，同一点在不同方向上的正应变是不同的，其中存在着正应变最大（最小）的方向，这个最大（最小）的正应变称为主应变，该方向为主方向。

主应变的大小为方程（3）的两个解：

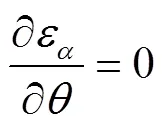
将式（1）或（2）代入方程（3），不难获得主应变的值：

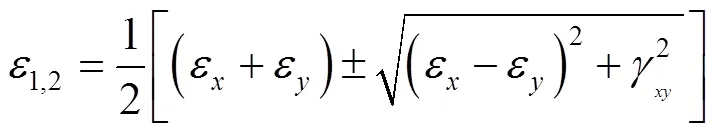
对于直角应变花（三个方向分别为0，45，90，对应的应变分别计为ε1，ε2，ε3），其主应变为：

对于三角形应变花（三个方向分别为0，60，120，对应的应变分别计为ε1，ε2，ε3）, 其主应变大小为：

式（5）、（6）为平面问题中主应变的测量模型（只列出了两种应变花型式，当采用其他型式的应变花时，可写出相应的测量模型）。显而易见，这些测量模型是非线性的，当进行不确定度评定时，基于一阶Taylor级数展开的LPU方法是不适用的，以下引入二阶LPU方法。

2 二阶LPU方法[11—12]

设导出测量量是个直接测量量（1，2，…，X）作用于测量模型的输出，如图1所示，则测量模型（测量函数）可以表述为：

如果用测量函数的二阶Taylor级数展开来近似表示导出测量量，则有：

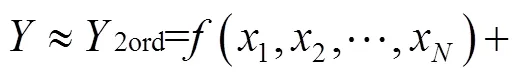
式中：x是直接测量量X的期望值（均值）。

若个直接测量量（1，2，…，X）均为统计独立，则对式（2）两边进行期望值计算，得到：

式中：(x)为直接测量量X的合成标准不确定度。

将式（8）和（9）的两边分别相减后取平方，然后计算相应的数学期望，有：

式中：γ和κ分别为直接测量量X的偏度和峭度，分别用三阶和四阶中心矩定义：

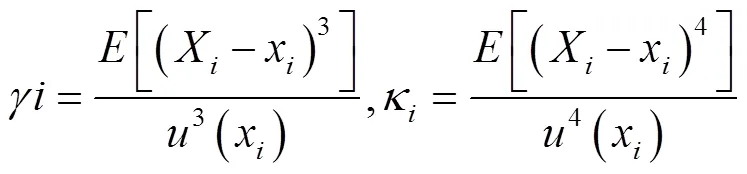
式（9）—（11）组成了基于LPU方法的不确定度传递的二阶计算公式。当测量模型为线性关系或近似线性关系时，式（9）和式（10）的右边仅保留有第一项非0，其余各项均为0，这样便简化为一阶LPU计算公式。

如果作为测量模型输入的直接测量量统计特性已知或可以假设，那么式（11）描述的偏度和峭度便容易求得，这样便可以由公式（10）评定导出测量量的合成标准不确定度。对于式（5）和式（6）描述的测量模型，其直接测量量均为应变花各个方向的应变测量量，假设其满足正态分布是合理的一种工程考虑，这样其偏度和峭度为0和3[13]，于是式（10）简化为：

3 二阶LPU方法在主应变测量不确定度评定的应用

将式（5）、（6）描述的主应变测量模型分别应用于式（10）或式（12），便可以获得主应变的不确定度评定结果。

直角应变花测量时的主应变不确定度为：

三角形应变花的结果为：

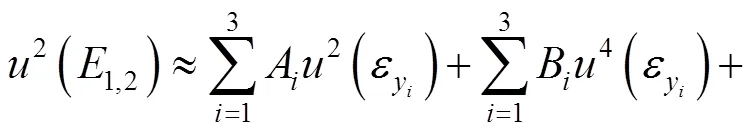
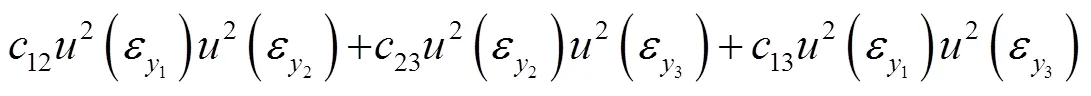
式中：

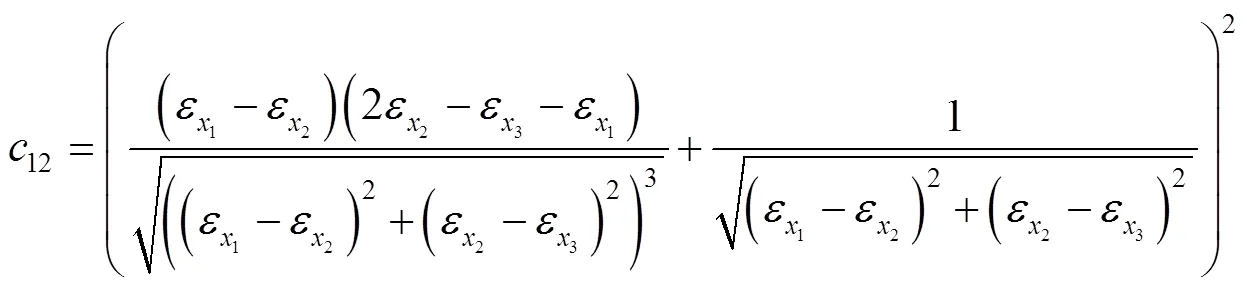
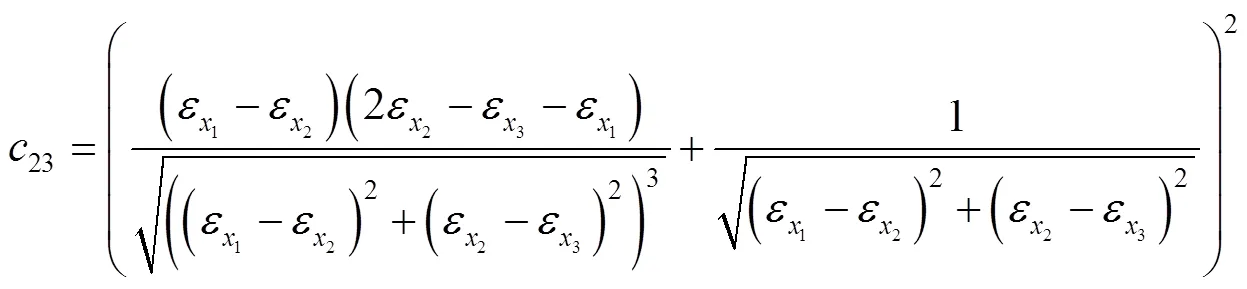
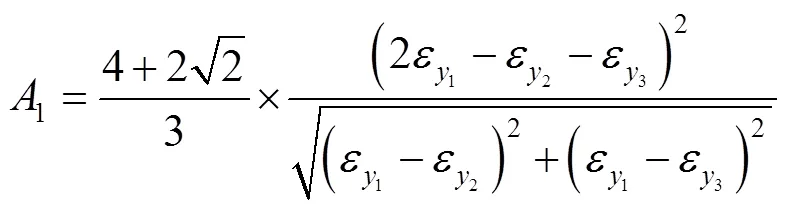
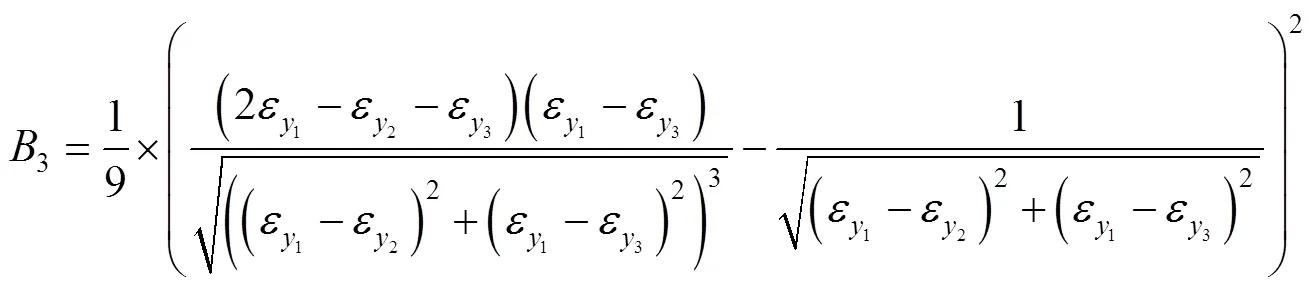
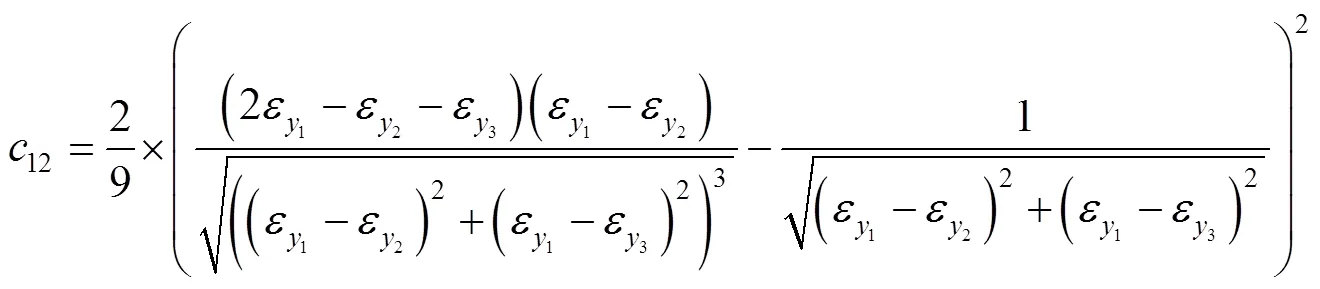
4 算例及分析

算例1，应变花三个方向应变测量均值相当，三个方向应变测量的测量不确定度相同，其主应变的均值和不确定度评定结果列入表1、表2中。其中，表1为直角应变花的主应变评定结果，表2 为三角形应变花的相关结果。为了比较，表1、表2中同时也列出了一阶LPU方法相应的评定结果。

算例2，当应变花三个方向的应变测量均值相差较大时，三个方向应变测量的测量不确定度相同，对应的主应变的不确定度评定结果列入表3和表4中。其中，表3为直角应变花的主应变评定结果，表4为三角形应变花的相关结果。同样的，表3、表4中同时也列出了一阶LPU方法相应的评定结果。

观察表1—4的数据不难发现，当应变花三个方向的应变测量结果相近时，文中方法与一阶LPU方法获得的主应变的不确定度评定结果存在明显的差异，两种应变花测量情况下都有这种现象。这表明，在特定情况时，一阶LPU方法不适合于主应变的不确定度评定（尽管文中讨论不足以说明二阶LPU方法获得的不确定度一定是精确的，但是其比一阶LPU方法具有更高的精度是不容置疑的）。另外，主应变的不确定度与应变花各测量方向应变的不确定度之间则没有明显大小关系。当应变花三个方向的应变测量结果相近时，主应变不确定度评定结果在数值上都大于应变花测量的不确定度。

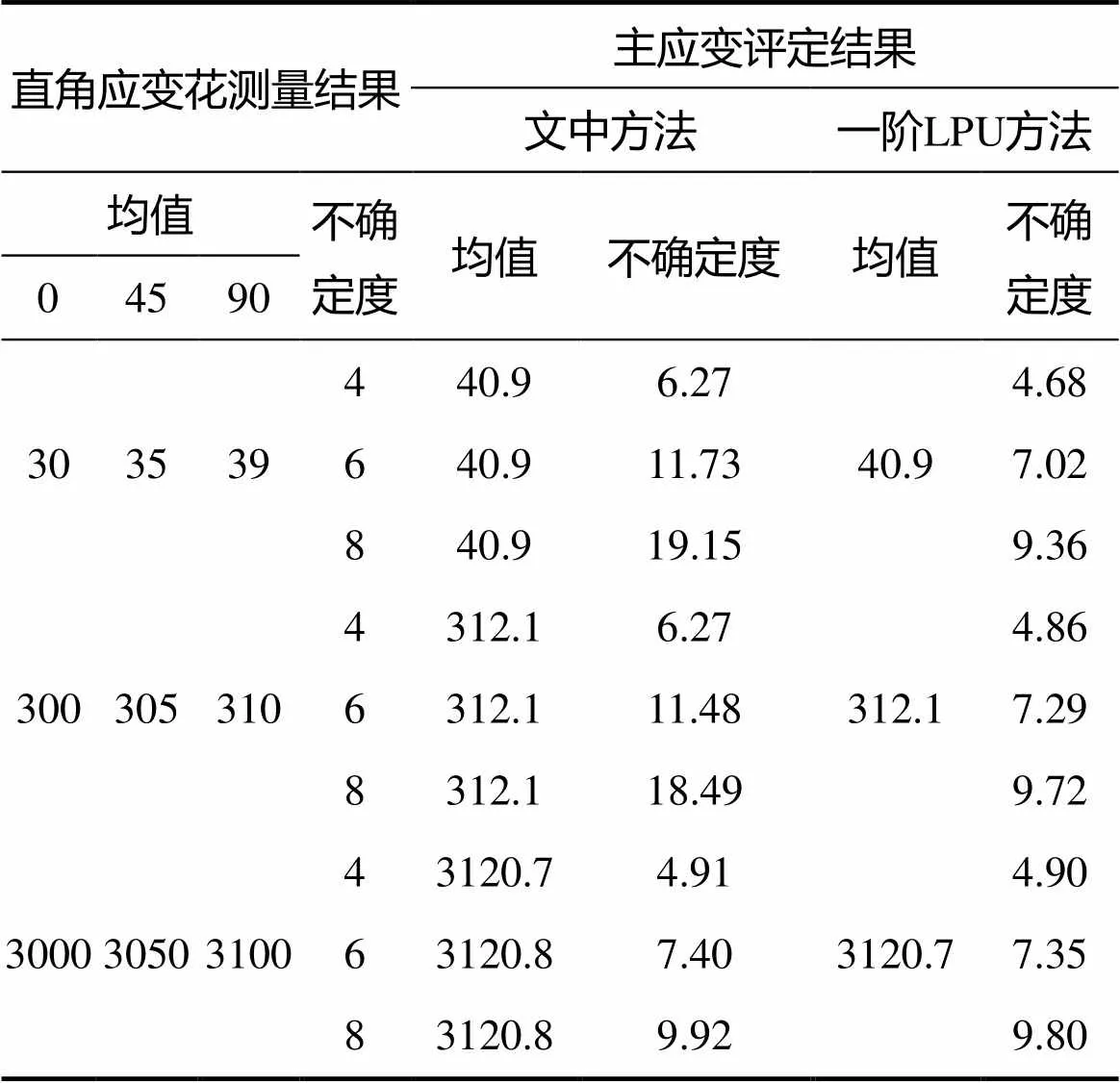
表1 应变测量值相近时主应变不确定度（με）评定（直角应变花）

表2 应变测量值相近时主应变不确定度（με）评定（三角形应变花）

表3 应变测量值相差时主应变不确定度（με）评定（直角应变花）

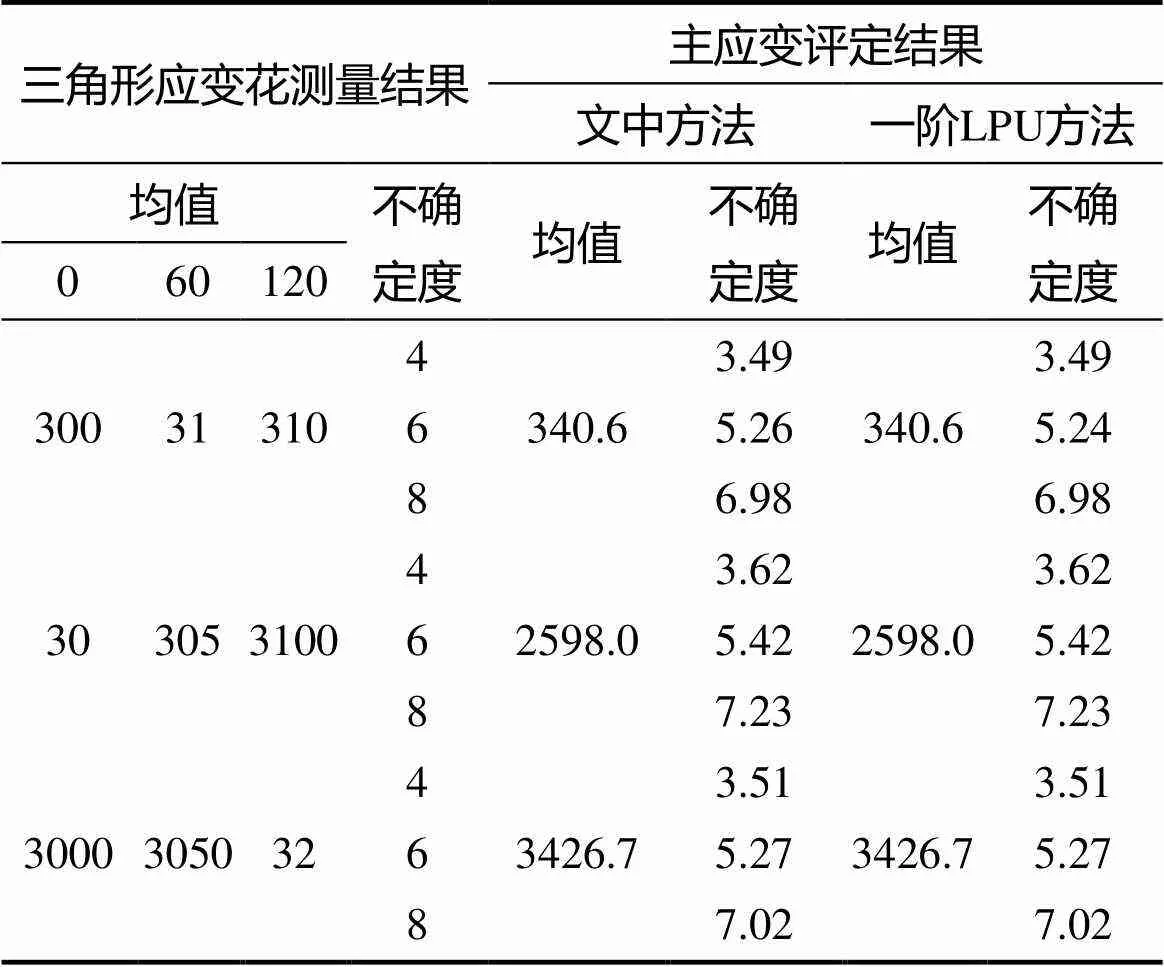
表4应变测量值相差时主应变不确定度（με）评定（三角形应变花）

当应变花三个方向的应变测量结果相差较大时，文中方法和一阶LPU方法获得的主应变测量不确定度评定结果相差不大，这时，可以采用一阶LPU方法来评定其主应变测量不确定度。简单对式（13）、（14）中的系数进行量级分析，不难发现：当应变花三个方向的应变分别相差一个量级时，系数都是一个小量，因此其主应变测量不确定度的二阶LPU评定结果与一阶结果相差不大。

5 结语

文中采用基于Taylor级数二阶展开理论的LPU方法，实现了平面问题中主应变的标准不确定度评定。几种典型测量数据的算例表明，当应变花的三个方向测量值相近时，二阶LPU方法与一阶LPU方法所得出的主应变不确定度评定结果有明显的差异，而当应变花三个方向测量值相差较大时，两种方法获得的主应变不确定度评定结果相差不大。

文中讨论是在假设应变花三个方向的应变测量量均为正态变量时得出的，这种假设一般情况下是能够满足的。当需要考虑应变测量量的其他概率分布影响时，依然能够采用类似分析来讨论主应变的不确定度评定，只是这时需要根据式（11）先求出其偏度与峭度参数。

文中讨论没有涉及主应变的扩展不确定度，是因为即使测量量是正态分布变量，但是其主应变的概率分布依然是复杂的，因此其扩展因子的确定并不容易。

[1] BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, and OIML, Evaluation of Measurement Data – Guide to the Expression of Uncertainty in Measurement (GUM 1995 with minor corrections). Joint Committee for Guides in Metrology, JCGM 100:2008

[2] GJB 3756A—2015, 测量不确定度的表示及评定[S].

[3] JJF 1059—1999, 测量不确定度的评定及表示[S].

[4] 黄波, 刘杰, 罗天元, 等. 固体发动机药柱应力应变仿真与试验验证研究[J]. 装备环境工程, 2015, 12(1): 15-19

[5] 黄旌, 刘成武, 魏东, 等. 光纤FBG传感器实施大应变标定方法的探讨[J]. 装备环境工程, 2013, 10(4): 86-89

[6] 张红星. 复杂应力状态下应变测量和数据处理方法探析[J]. 中国测试技术, 2006, 32(2): 52-55

[7] ARPIN-PONT J, GAGNON M, TAHAN S A, et al. Strain Gauge Measurement Uncertainties on Hydraulic Turbine Runner Blade[J]. Earth and Environmental Science, 2012, 15: 1-10.

[8] ARPIN-PONT J, GAGNON M, TAHAN S A, et al. Methodology for Estimating Strain Gauge Measurement Biases and Uncertainties on Isotropic Materials[J]. Jouanal of Strain Analysis, 2015, 50(1): 40-50

[9] KALITA K, DAS N, BORUAH P K, et al. Design and Uncertainty Evaluation of a Strain Measurement System [J]. Journal of Metrology Society of India, 2016, 31(1): 17-24

[10] 杜雅飞, 高炳军, 张及瑞. 内压球壳大开孔接管区电阻应变测量中不确定度的评定[J]. 中国测试技术, 2004, 30(5): 23-25

[11] YE C K, ARVIND R, MELANIE P-L O, et al. Standard Uncertainty Evaluation of Multivariate Polynomial[J]. Measurement, 2014, 58: 483-494

[12] 胡益平. 材料力学[M]. 武汉: 武汉大学出版社, 2013: 177-188.

[13] WILLIAM F R, LEROY D S, DON H M. Mechanics of Materials[M]. New York: John Wiley & Sons, 2007: 129-133.

[14] MEKID S, VAJA D. Propagation of Uncertainty: Expressions of Second and Third Order Uncertainty with Third and Fourth Moments[J]. Measurement, 2008,41: 600-609

[15] MARTINS M A F, REQUIAO R, KALID R A. Generalized Expressions of Second and Third Order for the Evaluation of Standard Measurement Uncertainty[J]. Measurement, 2011, 44: 1526-1530

[16] FRÉDÉRIC K, DAVID D. Vibration Fatigue and Simulation of Damage on Shaker Table Tests: The Influence of Clipping the Random Drive Signal[J]. Procedia Engineering, 2013, 66: 549-564.

Estimation of Measurement Uncertainty for Principal Strains in Plane Field

ZHU Xue-wang, ZHANG Si-jian, LIU Qing-lin, NONG Shao-ning

(Institute of Systems Engineering, CAEP, Mianyang 621999, China)

To assess the measurement uncertainties of principal strain in plane field.A measurement model of nonlinearity transmission was established for the principle strain. The Law of Propagation of Uncertainty (LPU) approach based on second order Taylor expansion was applied to analyze the measurement uncertainty of the principle strain. The measurement models were established for two typical strain rosettes with the principle strain as the output, the values measured in the three directions of the strain rosettes as the input and the LPU was applied to the models. Numerical examples were designed to illuminate the procedures and methods of assessment and to compare with the first order LPU estimations.When strain rosette strain measurements were close in three directions, uncertainty estimation results of the principal strain obtained through this method and the method of first-order LPU had obvious difference. That of the principal strain was greater than that of the strain rosette in numerical value. When strain rosette strain measurements differ in three directions, the results obtained through this method and the first-order LPU method has little difference.In special circumstances, the uncertainty value of principal strain is higher than those in any direction of rosette and different from the first order evaluations by one time.

principal strain; measurement of uncertainty; second order LPU approach; strain rosette; strain state theory

10.7643/ issn.1672-9242.2017.10.018

TJ01；O211.9

A

1672-9242(2017)10-0092-06

2017-05-01；

2017-05-21

朱学旺（1963—），男，湖北鄂州人，研究员，主要研究方向为复杂结构动力学及振动环境试验。