高中数学几何解题技巧之“数”“形”结合途径分析
2017-11-09盛雨瑶湖南省长沙市南雅中学
盛雨瑶 湖南省长沙市南雅中学
高中数学几何解题技巧之“数”“形”结合途径分析
盛雨瑶 湖南省长沙市南雅中学
几何是高中数学知识学习过程中的重点,同时难点。在数学几何类型的题目当中,常常与方程、函数以及不等式结合起来,在这样的情况下加大了几何解题的难度。学生在几何学习的过程中,由于对相关定理以及判断方法掌握不全面,导致了在解题的过程中出现了一定的困难。通过数形结合的方式能够在最大程度上提高解题的效率以及技巧,从而有力提高学生数学成绩。基于这样的背景之下,本文对数形结合技巧在高中数学几何当中的具体运用进行了分析,以此指导相关学习活动的顺利进行。
数量关系 几何解答 数形结合 运用
高中数学几何知识点的综合能力较强,部分学生由于未能全面掌握相关的知识点,导致了在解题的过程中出现了一定的困难。运用数形结合的方法就能够将相关的数量关系直观的表示出来,学生在解题的过程中才能够对数量关系进行清楚、有效的分析,从而提高解题的效率以及解题的技巧。
1 基本概念以及解题思路介绍
关于几何求解,基本定义就是通过代数的方式对相关的数量关系进步分析,同时将各个数量关系之间的性质以及特点通过相关的式子表示出来。在高中几何题型分析的过程中,主要有两种形式,第一就是对平面几何问题进行分析求解;第二种就是对立体几何问题进行分析求解。平面几何和立体几何的根本区别就是前者在二维坐标上进行分析,后者是在三维坐标上进行分析,通常情况下在三维坐标上将几何的数量关系表示出来将会使数量关系更加直观以及具体,同时也会大大提高学生对数量关系的分析能力以及解题的效率。
学生在对几何问题进行求解的时候,首要的一点就是要理清解题的思路。根据题干当中给出的已知条件或者是通过推导得出的隐含条件,将数量之间的关系进行充分分析。然后再通过数形结合的方式将几何数量之间的关系通过图形的形式表示出来,在这样的情况下学生就能够很快地找到解题的切入点。学生在解题的过程中可以按照以下具体的思路进行分析:第一就是分析题干当中给出的已知条件建立解题的概念和方法;第二就是将题干当中数量关系的几何意义进行构建;第三就是将几何数量关系通过图形直观的表示出来;第四就是根据图形所表现出来的数量关系将方程表达式解答出来。
2 具体的运用
根据相关的教学实践以及学习活动证明,运用数形结合的思维模式以及解题方法对解决平面圆相关的几何问题有着很大的帮助,通过数形结合的模式,能够将平面圆当中的数量关系直观、充分的表示出来。这是因为在解决平面圆这一类型的题目的时候,主要解决圆与直线、圆与圆之间的位置关系以及平面圆的方程等问题,这些问题都可以通过建立图形的方式来进行解决。但是在解题的过程中,学生只有掌握了解题的步骤才能够对相关的问题进行有针对性的解答。在这个过程中,学生可以通过数量关系建立图形模型,然后再根据图形对数量关系进行分析,运用这种方法进行平面圆几何问题解答,是基本的方法之一。下面本文就将这种解题模式运用到具体的例题当中进行分析,以此来更好地体现出数形结合解题模式的优点。
例1:已知曲线有两个不同的相交点,根据已知条件求出k的取值范围。与直线
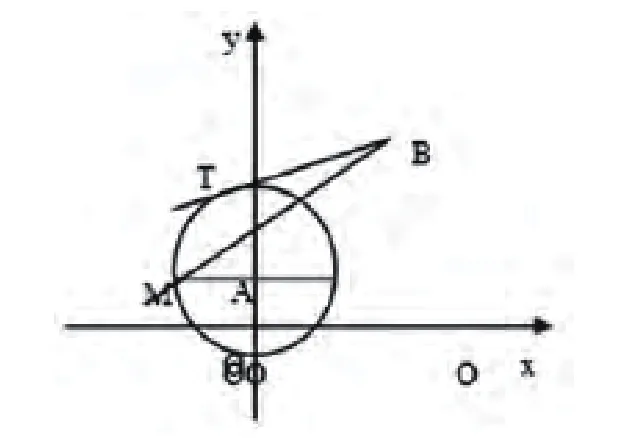
图1
解题思路:在解答这道题之前,学生应对这两个方程式进行观察,然后在此基础之上对进行变形就可以得到根据这个变形过后的方程式就可以得出点A(0,1)是曲线的圆心,这个圆的半径是2。同时根据可以得出y的值域是大于1的,所以可以推断出这个圆是一个上半圆。
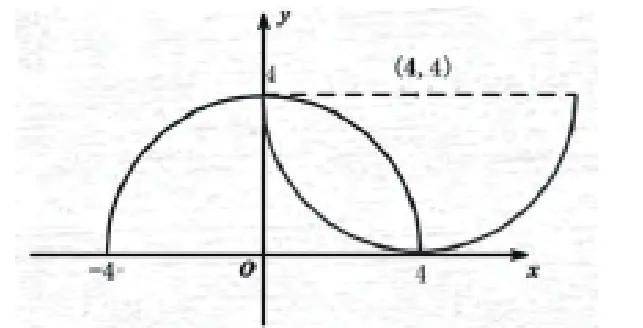
图2
解题思路:学生在解答这一道题的之前,首先还是要对这两个方程式进行观察,然后在此基础之上对原不等式进行变形,因此就可以得到:根据不等式的特点令,然后将进行再次变形,就可以得出:,根据对这两个式子进行观察可以得知,其所体现出来的图形都是半圆,根据图形可以得出两个半圆相交的点就是原不等式的解集,所以原不等式的解集是{x|0<x<4}。
数形结合的解题方法在高中几何当中运用十分广泛,对数形进行有效的结合,不仅能够将几何数量关系直观的表示出来,提高解题的效率,同时还能使学生加深相关知识点的记忆能力以及理解能力,从而提高学生解题的技巧。在平时的学习当中,应该加强数形结合相关题目的练习,通过大量的练习总结解题的经验和技巧,从而不断提高数学成绩。
[1]张艺璇.关于高中数学几何解题技巧之“数”“形”结合策略[J].亚太教育,2015,34:73.
