简述圆周运动综合题的解题策略

熊香花 湖南省宁乡县第一高级中学

简述圆周运动综合题的解题策略

熊香花 湖南省宁乡县第一高级中学

在学习高中物理时，圆周运动方面的综合性习题常常让我们感觉到非常困难，经常是无从下手。为了缓解这一现状，笔者围绕圆周运动涉及到的具体知识点展开，通过列举例题的形式，探索了圆周运动综合题的解题策略，希望能够给同学们以帮助。

圆周运动 综合题 解题策略

圆周运动综合性习题解答的关键在于分析，并要在学习的过程中掌握必要的方法和技巧，能够熟练应用圆周运动的相关规律。当具备了上述能力之后，综合性的圆周问题便能够进行顺利解答了。

1 圆周运动具体知识点介绍

在高中物理知识学习中，与圆周运动相关的具体知识点主要有线速度、角速度、周期、频率、转速、向心加速度、向心力、匀速圆周运动以及非匀速圆周运动等。一般而言，线速度是指物体在做圆周运动时，用来描述其运动快慢的物理量，线速度是一个矢量，其运动的方向是圆周切线方向。角速度是指物体围绕圆心转动快慢的量，角速度与线速度之间的关系表达式是v=r。向心加速度的方向总是指向圆心的，但其方向始终在变，而向心力是根据力的作用效果而命名的。与向心力相关的公式是匀速圆周运动是指线速度大小恒定，其运动力学特征是v、a的大小不变，T也不变，不变，但v、a的方向是一直在发生变化的。匀速圆周运动实质上是一种加速运动，其动力学特征是合外力等于向心力，方向也始终是指向圆心的，F=m=m2r。非圆周运动的线速度大小是要发生变化的，其表达式是F=m=m2r。

总之，在高中物理学圆周运动知识学习中，其涉及的具体内容众多，题型种类多样，不同的题型其解答思路不同，在学习时要注意加以区分并记牢各题型特征和相关计算公式，而不能将其混淆，不然，便很难准确解答出相关题目。圆周运动综合题无非就是将各具体知识点糅合在了一起，将具体问题综合在一起或者是将部分问题的结果作为过渡条件，而让我们来进行解答。只要我们准确掌握了各具体知识点，弄清楚了具体知识点的原理和规律，能够熟练应用具体知识点的公式，综合类问题便能够做到迎刃而解。

2 圆周运动综合题解题策略分析

在分析圆周运动综合题解题策略时，笔者主要采取的方式是列举例题，通过例题的具体分析阐述来说明自己的解题经验，希望能够借此帮助同学们更好的解答圆周运动综合题。

2.1 圆周运动与机械能守恒类综合题

例题1：在图1中，如果要让小球滑到光滑的离心轨道顶端，并且还要让其固定在顶端，一直不掉下来，求小球需要在斜轨的多高地方，便开始静止下滑。

解析：此题并不是单独的考察某一个知识点，而是将圆周运动与机械能守恒两个知识点结合在了一起。因此，可以将此题分成两部分，进行分别考虑。第一部分，分析圆周运动问题，当小球在离心轨道顶端时，其会受到两个力的作用，分别是重力和轨道对小球的压力。经过深入分析之后可以发现，这两个力的方向都是竖直向下的，并且这两个力的合力就是小球在运动中所受到的向心力。我们知道，在小球的运动中，其重力本身是不会变化的，而轨道对小球的压力却与速率有关，而速率与向心力之间又是呈正比关系。当小球的运动速率值小到一定程度时，轨道对小球的压力就可以忽略不计了。而要保证小球不掉下来，就必须要让小球的向心力大于或者是等于其重力，而不能够小于其重力。第二部分是机械能守恒，由于小球在运动过程中只会受到自身重力的影响，而不会受到其他的力的影响，所以，小球的运动是遵循机械能守恒定律的。具体解答过程如下：

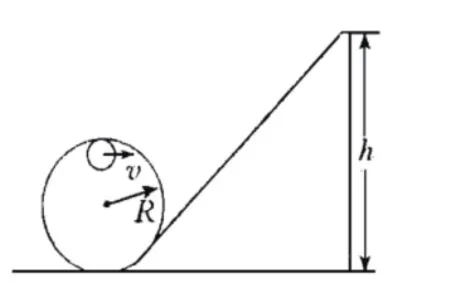
图1

解：假设小球在运动中不掉下来的速率是v，此时小球的重力等于向心力，并且轨道不会对小球产生任何作用，

因为，小球运动符合机械能守恒定律，

所以mgh=mg(2R)=mv2，

得到mgh=2mgR+mgR，

所以，小球需要在斜轨的 R处便开始静止下滑。

2.2 弹性势能、圆周运动以及斜抛运动类综合题

弹性势能、圆周运动以及斜抛运动类的综合题也是比较常见的，在做题或者是考试中我们也会常常遇到。在解答这类问题时，需要结合具体的问题情境，对其做三部分分析，对每一部分的知识点都进行全面考虑，得出准确信息，然后再进行作答。由于篇幅的原因，笔者在此就不列举例题了。总之，在解答圆周运动综合类题目时必须要重视分析，根据具体问题情境，分析出要考的知识点，或者是题目中所涉及到的知识点，将其先提炼出来，然后结合具体题设条件及所学知识，一一对应，掌握物体运动的向心力，受力情况，是否遵循能量守恒定律等，然后分部分、分步骤的进行作答。

经过笔者的自己总结发现，圆周运动综合题的重点在于分析阶段，当分析清楚了各部分所涉及到的知识点后，再进行解答就很容易了。并且，圆周运动综合题的解题过程和计算步骤都相对简单，所以，在积累解题经验时，要更加注重原理的分析，将投注力置于分析上。

[1]张平.师生对话探求圆周运动临界态[J].科学教育,2012,(05):73-74