基于平面几何性质的向量问题思考
2017-11-09彭雪纯湖南省长沙市麓山国际实验学校
彭雪纯 湖南省长沙市麓山国际实验学校
基于平面几何性质的向量问题思考
彭雪纯 湖南省长沙市麓山国际实验学校
高中学习,几何是十分重要的知识点,具有很强的包容性。而向量问题能够对我们的逻辑思维进行培养,具有着代数和几何的双重性质,因此这种题型在高考中十分的常见。本文以实际例题为基础,对平面几何性质的向量问题进行了深入的思考。
向量 平面几何 例题解析
1 距离的相关概念
向量模长是两点之间距离的表现,对这种模长进行理解与考核,是向量几何性质中最根本的呈现。
例题1:已知e1,e2是空间单位向量,而e1e2,若是空间向量b满足了be1=2,be2=,并且对任意x,y∈R,我们在对这道题目进行仔细阅读之后,可以得知能够使用代数化方式进行解答,不过相对复杂,并且也不能够呈现出向量几何性质。其首先要理解的是b的重点是处在和e1,e2形成平面,Ian的垂线上运动,经由平面向量相关的定理能够知道(xe1,ye2)体现的向量和e1,e2处在同个平面中。而表示的则是(图1)中在B进行任意移动时,距离最小时当且只当Q的位置是线和面的垂足,以三角形方面的定理可以知道这个时候x0=1,y0=2。因此在这道题的关键是对距离的理解,对其进行运用和构图就是解题的突破口。
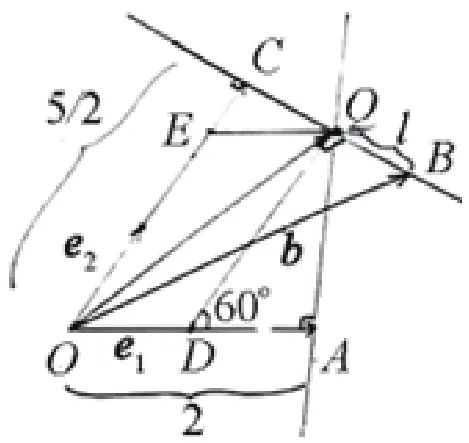
图1
2 平行四边形的性质
我们学习了平面四边形知识后,会了解到一个关键性质,即对角线平方和等于邻边平方和的2倍。在这个性质上就可以知道向量和之差是平面四边形最基本的几何表现。在这个性质的基础上,对向量问题进行解答就十分的容易。
例题2:如图2,CD两个点在△PAB的边AB之上,AC=BD若是∠CPD+90°,并且PA2+PB2=10,那么2AB+CD最大值是多少?
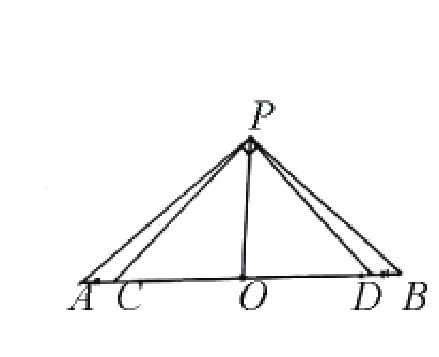
图2
解析:取CD重点O,在这个基础上连接PO,由于PA2+PB2=10,因此 2(PO2+AO2)=10,又因为 AO=AB,PO=CD,所以2([)2+()2]=10,因 此 AB2+CD2=20.记 x=AB,y=CD, 则 就 会 有x2+y2=20,Z=2x+y,使用线性定理能够得到(2x+y)max=10这道理是使用两个平行四边形对角线的特征。使用上面的结论进行有效的转化,进而减少了对题目的运算量。
3 极化恒等式
这个等式是对向量数量积和向量和之差之间关系进行体现的式子,在这个基础上进行解题,就能够避免了内部凌乱的预算关系出现,从而实现了便捷解答问题的目的。
解析:经过对题目的阅读之后可以得知题目中出现了a-c和ac,所以在a+c的基础上就能够得知这三者之间一恒等关系:对于a+c而言,在△OAC之中,取AC中点M,那么所以在对ac的最大值进行求解时,只用求的最大值就行。在这个圆中,因为AC=3,因此我们就能够知道OM经过圆心时获取最大值,在这个基础上就能够得到所以代入就能够得到ac最大值是(92-9)=18。解此题时,我们知道,计划恒等式的存在就不需要在内部对数量关系进行转换,在日常学习以及考试中,这种题型比较常见。在遇到这种问题时要对题目进行详细的阅读,以此判定这道题是否能够使用计划恒等式的方式对题目进行解答。合理运用这种方式能提升我们对知识的运用能力,和解题速度。
4 几何图形的构成
对向量几何意义进行考查时,离不开对几何图形的构建,这其中常见的几何图形是对向量问题进行解决的关键所在。我们在解题的时候要对几何图形进行仔细观察,还需要掌握几何图形的相关性质,例如三角形和圆的结构等等。
解析:向量ab满足于夹角120°,并且a-c和b-c夹角是60°,使用四个点公圆进行图形的构建,如图3,设=b,则∠ACB=60°,由此可知点C轨迹是优弧上面的一个动点,在点C是优弧中点时,取得最大值,其即为OABC四点处在圆的直径,在这个基础上就能够得到而根据三角形的正弦定理就能够得到:
平面几何是考察我们数学知识区分和运用能力,而把向量问题中存在的平面几何性质进行研究,在这个基础上就能够让我们在几何性质的基础上进行向量题目的解答,从而在解答过程中对我们的解题思路进行正确的引导,开辟出在解题中的新思路。
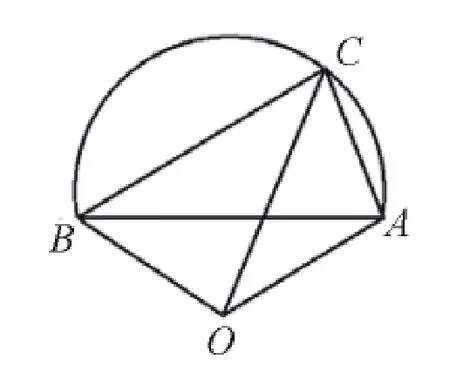
图3
[1]印金凤.基于平面几何性质的向量问题思考[J].数理化学习:高中版,2016(10):10-12.
