一个优化的低阶多项式累加和问题求解算法

刘瀚文

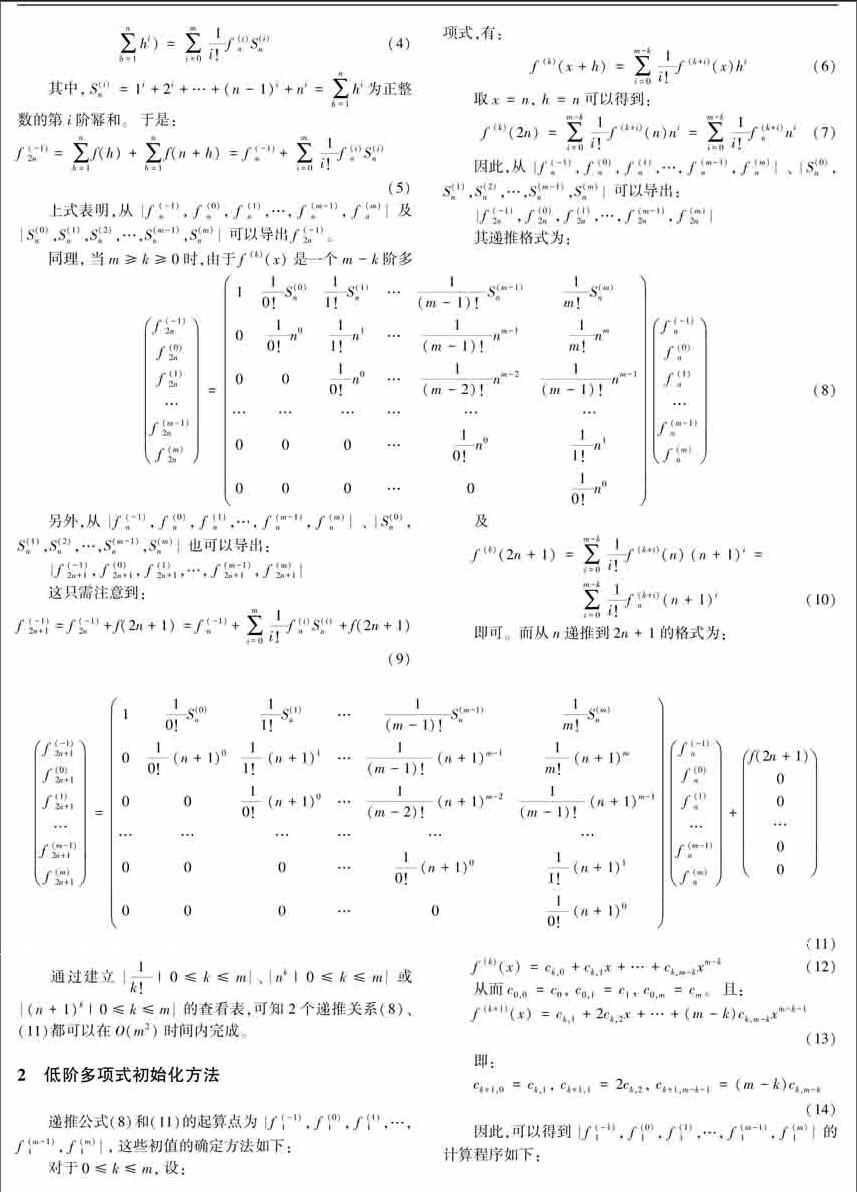
摘要： 本文针对低阶多项的多项式累加和问题∑〖DD（〗n〖〗k=1〖DD）〗f（k），其中f（x）=c0+c1x+…+cm-1xm-1+cmxm，當多项式幂次m较小，累加项数n较大的情况下，根据二分求解思想，设计了一种高效的递推求解方法，其时间复杂度为O（m2log n），而采用Horner格式计算多项式在每点的取值，再进行累加的朴素算法时间复杂度为O（mn），从而解决了在n[JP8]>>[JP]m时，大大提高了低阶多项的多项式累加求和的效率。

关键词： 多项式求值； 多项式累加和问题； Horner格式； 幂和问题

中图分类号：TP391.7

文献标志码： A

文章编号： 2095-2163（2017）05-0073-04

引言

在数论的世界中，对于多项式的相关性质研究是一个亘古不变的课题，吸引着一代又一代的专家和学者对其展开求知与探索。多项式求和问题是数论中的基础问题，在气象预报、生物计算等许多场景中有着重要应用。本文针对低阶多项的多项式累加和问题，即当多项式幂次m较小，累加项数n较大的情况下，根据二分求解思想，设计了一种高效的递推求解方法，重点解决了当n[JP8]>>[JP]m时，关于低阶多项的多项式累加求和的效率能够获得大幅提升的问题。而且仿真运行结果表明，该方法要明显优于传统的Horner算法。

方向进行推算，因此问题的空间复杂性为O（m）；[JP]而基于上述分析，可知对于任意给定的正整数n，上述折半方式的递推次数为O（log n），因此，∑〖DD（〗n〖〗k=1〖DD）〗f（k）的计算可以在O（m2log n）时间内完成。而通用的Horner朴素算法时间复杂度为O（mn），这就解决了当n[JP8]>>[JP]m时，大大提高了低阶多项的多项式累加求和效率的研究课题。

[参考文献

BARBEAU E J. Polynomials[M]. New York： Springer-Verlag， 1989.

[2] KNUTH D E. The art of computer programming（Sorting and Searching）[M]. 2nd ed. New Jersey：Addison-Wesley professional， 1998.

[3] Wikipedia. Polynomial[EB/OL]. [2017-08-21]. https：//en.wikipedia.org/wiki/Polynomial.

[4] SAUER T. 数值分析[M]. 2版. 裴玉茹， 马赓宇，译. 北京：机械工业出版社，2014.

[5] GREENBAUM A， CHARTIER T P. 数值方法：设计、分析和算法实现[M]. 吴兆金，王国英，范红军，译. 北京：机械工业出版社，2016.

[6] HORN R A， JOHNSON C R. 矩阵分析[M]. 2版. 张明尧， 张凡，译. 北京：机械工业出版社，2014.endprint