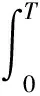一类分数阶边值问题解的存在性
2017-11-08李姗姗王智勇
李姗姗, 王智勇
(南京信息工程大学 数学与统计学院, 江苏 南京 210044)
一类分数阶边值问题解的存在性
李姗姗, 王智勇*
(南京信息工程大学 数学与统计学院, 江苏 南京 210044)
研究一类非齐次分数阶微分方程边值问题
其中,λ>0,h∈L2([0,T],RN)且h(t)≢0.利用山路引理和Ekeland变分原理,得到上述问题至少存在2个非平凡解.
分数阶边值问题; 山路引理; Ekeland变分原理
1 主要结果
考虑如下分数阶边值问题

(A) 对∀x∈RN,F(t,x)关于t是可测的,对a.e.t∈[0,T],F(t,x)关于x是连续可微的,且存在a∈C(R+,R+),b∈L1([0,T],R+)使得:
|F(t,x)|≤a(|x|)b(t),
|▽F(t,x)|≤a(|x|)b(t),
对∀x∈RN和a.e.t∈[0,T]成立.
当β=0,λ=0时,问题(1)退化为

上述边值问题具有较为简单的变分结构,其解的存在性和多重性已有很多结果,如文献[1-4].
当λ=0时,问题(1)则变为
2011年,Jiao F.等[5]首次给出了问题(2)的变分结构,利用极小作用原理和山路引理,得到问题(2)至少存在一个解.自此以后,位势函数F(t,x)在各种增长条件下,关于问题(2)解的存在性和多解性涌现了大量的结果,如文献[6-8]及其参考文献.
受上述结果的启发,本文利用山路引理及Ekeland变分原理,讨论了问题(1)的2个解的存在性.
定理1.1假设F满足条件(A),且存在常数r>2,μ>r-2以及Λ0>0,使得下列条件成立:





其中,Γ为通常的伽马函数,α=1-β/2;则当λ∈(0,Λ0)时,问题(1)至少存在2个非平凡解.
注1.1在文献[9]中,利用山路引理讨论了问题(2)在条件(A)、(A3)~(A5)及

本文考虑带扰动项h(t)的问题(1)多个解的存在性问题.事实上,扰动项h(t)的存在对弱解的多解性在本文中起着关键作用.
2 预备知识
下面介绍一些分数阶微积分的基本概念,并且给出问题(1)的工作空间和变分结构.
定义2.1[10]设γ>0,函数f(t)定义在[a,b]上,它的γ阶左和右Riemann-Liouville分数积分分别定义为:

和

其中右在[a,b]上逐点有定义.
定义2.2[10]设γ>0,函数f(t)定义在[a,b]上,它的γ阶左和右Riemann-Liouville分数导数分别定义为:

和

其中,t∈[a,b],n-1≤γ 记AC([a,b],RN)为绝对连续函数空间,对k∈N, ACk([a,b],RN)={f∈Ck-1([a,b],RN): f(k-1)∈AC([a,b],RN)}. 定义2.3[10]设γ≥0,n∈N,若γ∈[n-1,n)且f(t)∈ACn([a,b],RN);则函数f(t)的γ阶左和右Caputo分数导数于[a,b]上几乎处处存在,且分别定义为: 和 L2([0,T],RN),u(0)=u(T)=0,1/2<α≤1}, 易知它是自反的可分的Banach空间,其范数为 命题2.4[11]设0<α≤1,1 (3) 进一步,若α>1/p且1/p+1/q=1,则有 特别地,当p=2时,有以下2个不等式成立: (4) (5) 注2.1由(5)式,Eα上的范数‖·‖等价于如下定义的‖·‖α,即 引理2.5[5]设0<α≤1,1 定义2.6若对u∈Eα以及∀v∈Eα,有 则称u为问题(1)的弱解. 定义泛函φ:Eα→R为 λh(t)u(t)-F(t,u(t))]dt; (6) 根据条件(A),由文献[5]中定理4.1,可知φ∈C1(Eα,R)且有 (7) 进一步可知,u∈Eα为问题(1)的弱解当且仅当u为泛函φ的临界点. 引理2.7[5]若1/2<α≤1,则对∀u∈Eα,有 |cos(πα)|‖u‖α2≤ (8) 定义2.8[1]设X是实Banach空间,φ∈C1(X,R),如果{un}⊂X,φ(un)有界且φ′(un)→0(n→+∞);则称序列{un}⊂X为φ的(PS)序列.如果它的每一(PS)序列都有一收敛子列,则称泛函φ满足(PS)条件. 定义2.9[1]设X是实Banach空间,φ∈C1(X,R),如果{un}⊂X,φ(un)有界,且(1+‖un‖α)‖φ(un)‖α→0(n→+∞);则称序列{un}⊂X为φ的(C)序列.如果它的每一(C)序列都有一收敛子列,则称泛函φ满足(C)条件. 引理2.10[2](山路引理) 设X为实Banach空间,φ∈C1(X,R)满足(PS)条件,φ(0)=0,且有: (I1) 存在常数ρ,β>0,使得φ|∂Bρ≥β; (I2) 存在e∈XBρ,使得φ(e)≤0, 则φ存在一个临界值c≥β,且 注2.2由文献[12]可知,山路引理在(C)条件下依然成立. 为了叙述方便,令Ci(i=1,2,3,…)表示一系列不同的正常数. 引理3.1假设条件(A)、(A4)、(A5)成立,则泛函φ满足条件(C). 证明令X=Eα,首先证明{un}在X上有界.假设{un}是泛函φ的(C)序列,即{φ(un)}有界,且当n→+∞时,有‖φ′(un)‖α(1+‖un‖α)→0;则对∀n∈N有 φ(un)≤C1, ‖φ′(un)‖α(1+‖un‖α)≤C1. (9) 根据条件(A4),存在常数R1>0,使得对∀|x|≥R1以及a.e.t∈[0,T],有 F(t,x)≤C2|x|r. (10) 结合(10)式和条件(A),对∀x∈RN和a.e.t∈[0,T],可知 F(t,x)≤C2|x|r+g1(t), (11) (12) 由条件(A5),存在常数R2>0,使得对∀|x|≥R2和a.e.t∈[0,T],有 (▽F(t,x),x)-2F(t,x)≥C5|x|μ; 因此,再由条件(A),对∀x∈RN和a.e.t∈[0,T],可得 (▽F(t,x),x)-2F(t,x)≥C5|x|μ-g2(t), (13) 下面分2种情形进行讨论. 情形1若μ>r,利用Hölder不等式和带ε的Young不等式有 (14) 考虑(6)、(7)、(9)、(13)和(14)式有 所以可得 (16) 根据(12)、(16)式及Hölder不等式,可知 注意到,μ>r,因此‖un‖α有界. (17) 其中,p′=μ-r+2,1/p′+1/q′=1.利用(15)和(17)式可得 因此 (18) 由于μ>r-2,利用(12)、(18)式和Hölder不等式,并注意到ε的定义有 因此,‖un‖α有界. 综上所述,对于μ>r-2,总有{un}在X中有界. 最后证明{un}在X上有强收敛子列.因为{un}在X上有界,则存在子序列,不妨仍记为{un},使得在X上,有un⇀u.于是,当n→+∞时,有 〈φ′(un)-φ′(u),un-u〉= 〈φ′(un),un-u〉-〈φ′(u),un-u〉≤ ‖φ′(un)‖α‖un-u‖α- 〈φ′(u),un-u〉→0. (19) 由(5)式和引理2.5,可知{un}在C([0,T],RN)上有界;并且当n→+∞时,有‖un-u‖∞→0.因此,再依据条件(A),当n→+∞时,有 (20) 此外,由(7)、(8)、(20)式以及Hölder不等式有 〈φ′(un)-φ′(u),un-u〉= 所以结合(19)式可得,当n→+∞时,‖un-u‖α→0,即φ满足(C)条件. 引理3.2假设F满足条件(A2)、(A4),则存在常数ρ>0,β>0和Λ0>0,使得当‖u‖α=ρ,λ∈(0,Λ0)时,有φ(u)≥β. 证明根据条件(A2)、(A4)可知,存在常数ε1∈(0,|cos(πα)|),对∀x∈RN和a.e.t∈[0,T],有 C12|x|r. (21) 由(3)、(6)、(8)、(21)式及Hölder不等式有 λh(t)u(t)-F(t,u(t))]dt≥ 引理3.3假设F满足条件(A)、(A3),则存在e∈X且‖e‖α>ρ,使得φ(e)<0. 证明由条件(A3)知,存在常数ε2>0和R3>0,使得对∀|x|≥R3以及a.e.t∈[0,T]有 F(t,x)≥ 再由条件(A),对∀x∈RN和a.e.t∈[0,T]有 (22) (23) 根据(6)、(8)、(22)、(23)式和Hölder不等式,当s→+∞时有 λsh(t)u0(t)-F(t,su0(t))]dt≤ 所以,存在充分大的s0使得φ(s0u0)<0,取e=s0u0∈X,有φ(e)<0. 引理3.4假设条件(A1)成立,则 其中ρ由引理3.2给出. 证明由条件(A1)知,存在常数δ>0,使得对∀|x|≤δ以及a.e.t∈[0,T]有 F(t,x)≥0. (24) λsh(t)φ(t)-F(t,sφ(t))]dt≤ [1] MAWHIN J, WILLEM M. Critical Point Theory and Hamiltonian Systems[M]. New York:Springer-Verlag,1989. [2] WANG D B, YANG K. Existence of periodic solutions for a class of second order Hamiltonian systems[J]. Boundary Value Problems,2015,2015(1):1-14. [3] 张鹏. 一类次线性二阶Hamiltonian系统的无穷多解[J]. 四川师范大学学报(自然科学版),2010,33(5):588-591. [4] 居加敏,王智勇. 一类带阻尼项的次二次二阶Hamiltonian系统的周期解[J]. 四川师范大学学报(自然科学版),2015,38(3):329-332. [5] JIAO F, ZHOU Y. Existence of solutions for a class of fractional boundary value problem via critical point theory[J]. Comput Math Appl,2011,62(3):1181-1199. [6] BONANNO G. A critical point theorem via the Ekeland variational principle[J]. Nonlinear Anal,2012,75(5):2992-3007. [7] KONG L J. Existence of solutions to boundary value problems arising from the fractional advection dispersion equation[J]. Elect J Diff Eqns,2013,2013(106):1-15. [8] 陈静. 一类带渐近二次非线性项的分数阶Dirichlet边值问题解的存在性[J]. 应用数学学报,2015,38(1):53-66. [9] CHEN J, TANG X H. Existence and multiplicity of solutions for some fractional boundary value problem via critical point theory[J]. Abs Appl Anal,2012,2012(3):185-195. [10] ZHOU Y. Basic Theory of Fractional Differential Equations[M]. Singapore:World Scientific,2014. [11] XU L P, Chen H B. Multiple solutions for the nonhomogeneous fourth order elliptic equations of Kirchhoff-type[J]. Taiwanese J Math,2015,19(4):1215-1226. [12] IZYDOREK M, JANCZEWSKA J. Homoclinic solutions for a class of the second-order Hamiltonian systems[J]. J Diff Eqns,2005,219(2):375-389. Existence of Two Solutions for a Class of Nonhomogenous Fractional Boundary Value Problems LI Shanshan, WANG Zhiyong (SchoolofMathematicsandStatistics,NanjingUniversityofInformationScienceTechnology,Nanjing210044,Jiangshu) In this paper, we deal with the following nonhomogeneous fractional boundary value problem whereλ>0,h∈ ([0,T],RN) andh(t)≢0. Using mountain pass lemma and Ekeland’s variational principle, we prove that the above boundary value problem has at least two nontrivial solutions. fractional boundary value problem; mountain pass lemma; Ekeland’s variational principle 2016-09-22 国家自然科学基金(11026213、11571176) *通信作者简介:王智勇(1979—),男,副教授,主要从事非线性泛函分析的研究,E-mail:mathswzhy@126.com O175.1 A 1001-8395(2017)05-0615-06 10.3969/j.issn.1001-8395.2017.05.009 2010MSC:26A33; 35G60 (编辑 余 毅)

















3 定理的证明