大断面异形盾构隧道弯矩传递系数原型加载试验研究
2017-11-08朱叶艇
朱叶艇
(1. 上海隧道工程有限公司, 上海 200233; 2. 同济大学地下建筑与工程系, 上海 200092)
大断面异形盾构隧道弯矩传递系数原型加载试验研究
朱叶艇1, 2
(1. 上海隧道工程有限公司, 上海 200233; 2. 同济大学地下建筑与工程系, 上海 200092)
由于异形盾构隧道特殊的结构断面型式,管片设计暂无相关规范可循,故基于原型三环管片力学加载试验对异形盾构管片环向接头弯矩传递系数进行研究,研究结果表明: 1)随埋深增加,异形盾构管片结构整体刚度提升,但由于各接头刚度与相邻管片结构刚度比随埋深增加变化规律不一致,异形盾构管片接头弯矩传递能力呈部分减弱部分增强的现象; 2)同埋深条件下,随着侧压力系数的增加,除右拱腰处接头外,其余接头弯矩传递能力随着接头刚度与相邻管片结构刚度比的增大而逐渐增强; 3)随着埋深增加,各接头弯矩传递能力对侧压力系数的敏感程度逐渐减弱; 4)极限破坏后,异形盾构管片内外弧面裂缝的分布规律证明了明显的弯矩传递现象。
异形; 盾构隧道; 大断面隧道; 原型试验; 弯矩传递系数; 裂缝
0 引言
盾构隧道是一种由环向螺栓和纵向螺栓将管片拼接成型的结构体,而错缝拼装方式可显著提高管片结构的力学性能和极限承载能力[1]。研究表明,管片环向接头和纵向接头都具有铰的功能[2-4]。管片错缝拼装后内力会发生一定程度的变化,尤其是在相邻管片纵缝对应位置。由于纵向接头和管片环间摩擦的存在,不可避免地在管片结构纵向上发生弯矩的传递,而弯矩传递的效果通过弯矩传递系数进行衡量[5]。现阶段对圆形盾构管片弯矩传递系数的研究主要基于原型管片接头加载试验或整环管片加载试验。研究发现,弯矩传递系数的大小主要受管片环间接触特性、纵向螺栓强度和管片纵向约束条件等影响[6-7]。
Yukinori Koyama[5]提出了弯矩传递系数的计算方法。《日本隧道标准规范(盾构篇)及解释》[8]通过统计接头管片荷载试验结果,给出了圆形盾构隧道弯矩传递系数的建议范围。蒲奥[9]基于简化错缝拼装计算模型获得了管片接头弯矩传递系数,并由实测数据验证了数据的合理性。黄正荣等[10]通过梁-弹簧模型计算获得管片接头和接头相邻环位置管片弯矩值以及弯矩传递系数,并拟合出弯矩传递系数经验公式。封坤等[7]基于原型加载试验对南京长江隧道和广州狮子洋隧道管片弯矩传递系数进行研究,发现了横向刚度有效率和弯矩传递系数之间的关系。闫治国等[11]以青草沙水源地输水隧道工程为工程背景,通过管片接头原型荷载试验,对弯矩传递系数进行研究,发现弯矩传递系数随着外荷载的增大而减小。张银屏[12]基于壳-弹簧模型对地面出入式超浅埋盾构隧道管片结构进行分析计算,发现针对负覆土地层情况,弯矩传递系数可偏保守地取值为1。
国内外针对盾构管片弯矩传递系数的研究不多,且所得研究成果都是基于圆形隧道。异形盾构隧道断面类圆形且类矩形,未来主要应用于下立交、地铁车站和出入场线等浅覆土地下工程,其力学行为和破坏特征较圆形和矩形隧道更为复杂。由于特殊的断面型式、分块方式以及特有的高强度环向铸铁手孔构造,其接头传力机制应与圆形隧道存在一定差异。本文基于大断面异形盾构管片原型加载试验对其弯矩传递特性进行探索研究,并给出各个接头位置的弯矩传递系数范围,以期为将来异形盾构的优化设计提供有力的理论支持。
1 原型加载试验
1.1管片设计概况
异形盾构管片基于上海④号淤泥质黏土地层运营阶段设计,根据规范[13]要求,管片水土荷载采用水土分算方法,主要设计参数如表1所示。

表1 异形盾构设计参数
异形盾构隧道管片布置如图 1所示,管片宽10.7 m,高8.2 m,由8段弧组成(分别为上、下拱顶、底弧,左、右侧弧和4段角弧)。管片幅宽1.2 m,厚0.5 m,共6分块(分别为1块封顶块F、2块邻接块L1、L2和3块标准块B1、B2、B3),采用错缝拼装形式(见图 2),块之间采用4根M30直螺栓连接,环之间采用26根M33弯螺栓连接。接头序号的定义见图 1。
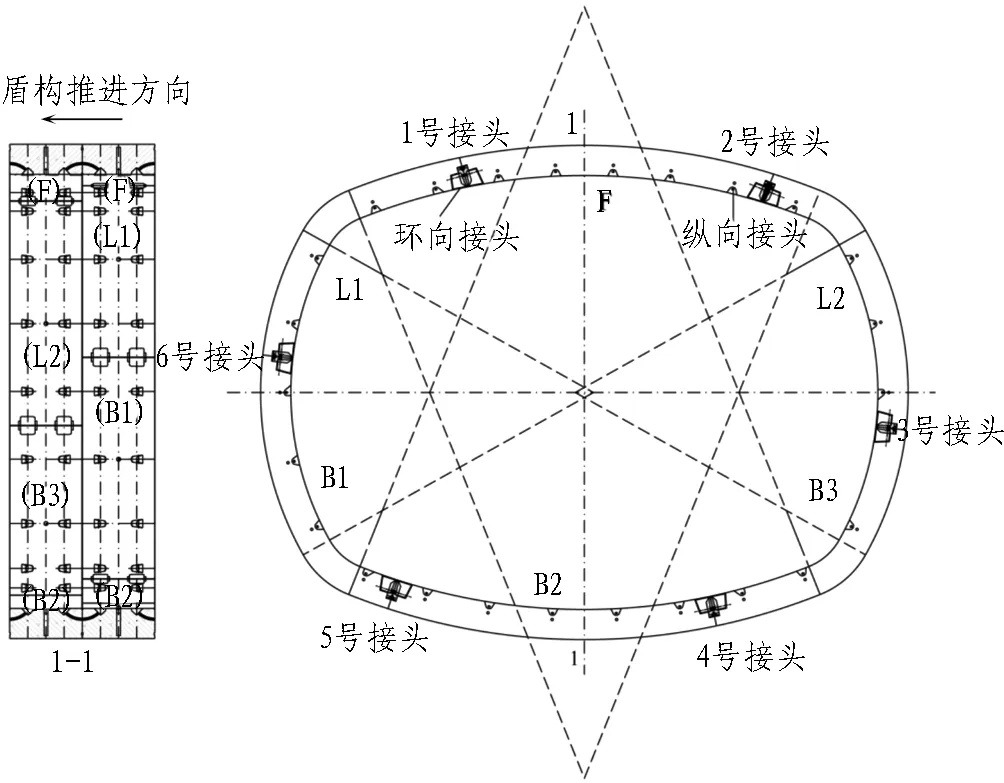
图1 异形盾构隧道管片布置图

图2 试验状态下管片错缝拼装
1.2原型加载试验概况
本次异形盾构管片原型加载试验将3环(包括2个半环和1个整环)管片错缝拼装后放置于可重构式钢结构加载反力架中轴线对称的8组颗粒型弹性橡胶支座上,如图 3所示。
根据文克勒弹性地基梁模型理论[14],地基可以看作是由无数不相联系的弹簧组成的体系。管片底部采用弹性橡胶支垫模拟土弹簧,其设计源于桥梁工程中梁与桥墩之间起缓冲和减摩作用的普通板式橡胶支座。每组橡胶支垫共4块,每块弹性橡胶支垫平面尺寸为400 mm×580 mm,由38 mm厚的板式橡胶和27颗橡胶颗粒柱组成。颗粒柱直径80 mm,高度25 mm,采用硬度为68°的橡胶材料。从图 4橡胶柱的荷载-压缩曲线可以看出,单颗橡胶柱弹簧刚度具备分段线性特征:当压缩量小于7 mm时,抗压刚度为2 046 kN/m,大于7 mm时为6 604 kN/m。数值模拟和原型试验结果显示管片底部位移量在7 mm范围内,故单颗橡胶柱弹簧刚度取值2 046 kN/m。综上,弹性支垫的线性特征符合弹性地基梁模型中地基弹簧的理念。

图3 钢结构加载框架
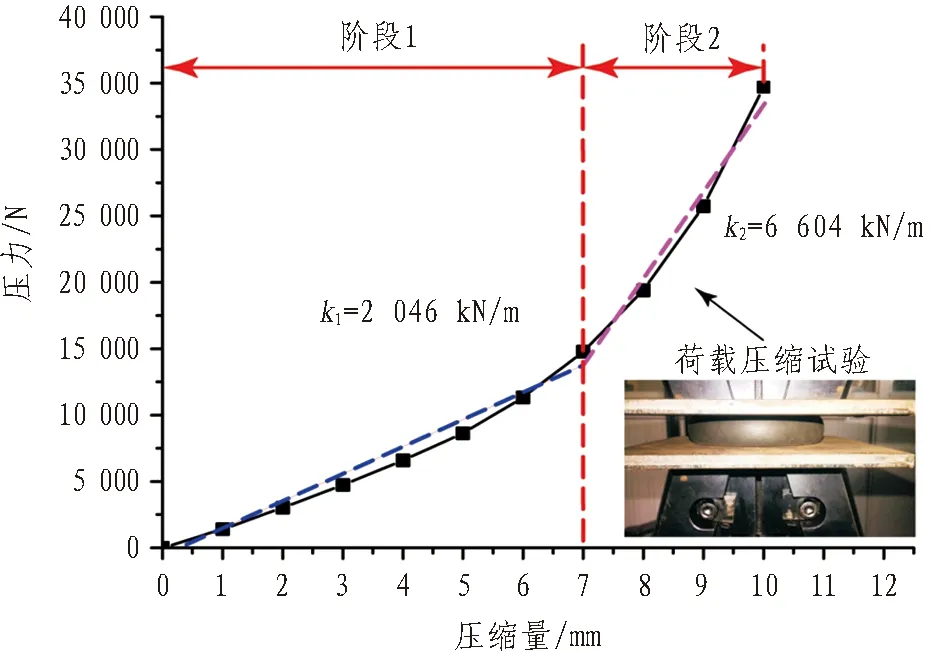
图4 橡胶颗粒柱荷载-压缩曲线
22组千斤顶加载点(每组4个千斤顶,半环1个,整环2个,共88个千斤顶)关于中轴线对称并环向分布于管片结构外弧面,采用PLC液压控制系统精确施加地层荷载,如图5所示。
30组纵向夹紧装置(每组由前、后夹板和4根拉杆组成,夹紧力为5 000 kN)环向分布于管片结构端面以施加管片纵向荷载并确保3环管片的整体稳定性。
为研究异形盾构管片弯矩传递能力和侧压力系数敏感性,本试验共设计7个试验工况,如表2所示。
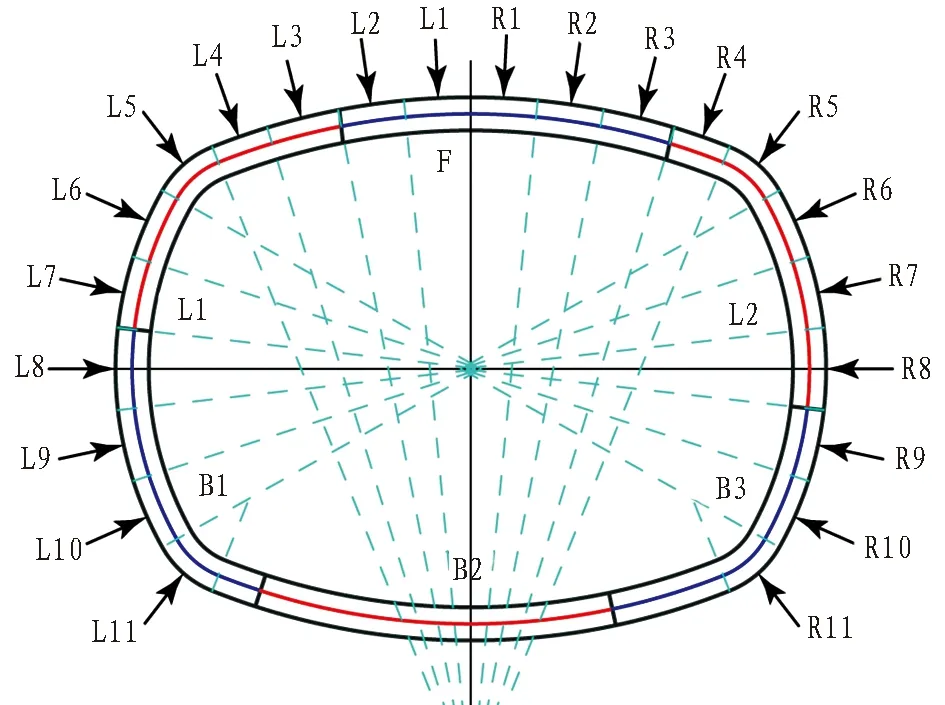
图5 荷载施加示意图

序号试验工况1 自重工况2 设计状态,侧压力系数0.43 设计状态,侧压力系数0.54 设计状态,侧压力系数0.65 设计状态,侧压力系数0.76 设计状态,侧压力系数0.87 极限破坏工况
1.3测试方法
由于国内外暂无管片环向接头弯矩精确测试或计算方法,故本次试验在近管片接头两侧内、外弧面等距布置混凝土应变和钢筋应变测点,通过计算获得接头两侧断面弯矩并取平均值的方式获得该接头弯矩值。同时在半环对应整环接缝位置内弧面布置混凝土和钢筋应变测点,计算获取半环测试断面弯矩值。测点布置如图6所示。

图6 测点布置示意图
其中,混凝土应变通过箔式应变片和振弦式表面应变计测点,见图7(a)和7(b),钢筋应变通过箔式应变片和振弦式钢筋计测定,见图7(c)。

(a) 整环接缝两侧混凝土表面测点

(b) 半环对应整环接缝处混凝土表面测点

(c) 接头两侧钢筋测点
2 弯矩传递系数计算方法
根据修正惯用法理论[15],实体管片截面计算弯矩Ms和接头弯矩Mj(见图8)可分别表示为:
Ms=(1+ξ)Μ;
(1)
Mj=(1-ξ)Μ。
(2)
式中M为实体管片弯矩Ms和接头弯矩Mj的平均值,即:

(3)
弯矩传递系数ξ为传递的弯矩ξM与平均值M的比值,表达式为

(4)
3 试验结果分析
3.1自重状态
自重状态下,管片结构不受水土荷载作用,各接头的弯矩和弯矩传递系数计算值如表 3所示。

图8 弯矩传递示意图

接头序号接缝两侧弯矩/(N·m)接头弯矩计算值/(N·m)相邻实体管片弯矩/(N·m)弯矩传递系数15171161389565501023370.28822514472722839337479950.09913-108612-95695-102154-1543800.203647069165865682781189830.27085711293568553407775350.18436-107732-83306-95519-1282520.1463
管片顶板和底板1号、2号、4号和5号接头处于正弯矩区,3号和6号接头处于负弯矩区。正弯矩区1号接头弯矩传递系数最大,为0.288 2,其次为4号接头和5号接头,最小为2号接头。自重状态下正弯矩区接头弯矩传递系数分布为0.099 1~0.288 2。负弯矩区3号接头弯矩传递系数大于6号接头,其值分别为0.146 3和0.203 6。
3.2设计状态
设计地层运营阶段条件下,各接头弯矩传递系数随埋深增加(3、5、8、10 m)的变化规律如图9所示。

图9 各接头弯矩传递系数随埋深增加的变化规律Fig. 9 Variation of bending moment transferring coefficients of every joint with buried depths
设计地层运营阶段异形盾构管片1号、2号、4号和5号接头处于正弯矩区,3号和6号接头处于负弯矩区。2号、3号和5号接头弯矩传递系数随覆土增加呈二次曲线增长趋势,而1号和4号接头弯矩传递系数随覆土增加呈二次曲线下降趋势,6号接头随覆土增加呈较弱的线性减小趋势。接头是管片结构最薄弱的位置,接头刚度对异形断面的受力和形变的影响尤为重要。合适的接头弯矩传递既可以发挥混凝土实体结构的承载能力,又能起到保护接头的作用。随着埋深的增加,管片外荷载随之增大,环向接头两侧管片之间咬合更为紧密,接头端面混凝土的摩擦和抗压性能以及环向螺栓的抗拉性能逐渐发挥,管片接头轴力增加,管片接头刚度随之增大,管片结构整体刚度也得以提升。文献[7]研究发现接头弯矩传递现象随着结构整体刚度的提高而逐渐减弱,而异形管片接头呈部分减弱部分提升的现象。究其原因,接头设置位置的选择对弯矩传递系数的影响较为重要,由于异形盾构管片采用错缝拼装方式,整环管片接头与相邻半环管片接头距离较近,故相邻管片结构刚度受自身附近接头影响较大,而并非常规意义上的实体管片截面刚度。当环向接头位于管片右拱肩、右拱腰和左拱脚(即2号、3号和5号接头位置)时,接头刚度与相邻管片结构刚度比随埋深增加而逐渐减小,接头弯矩传递现象趋于明显。反之,当环向接头位于左拱肩、右拱脚和左拱腰(即1号、4号和6号接头)时弯矩传递现象减弱。
总体上,正弯矩区管片接头弯矩传递系数为0.232 8 ~ 0.315 7;负弯矩区接头弯矩传递系数为0.153 8 ~ 0.221 1。
3.3侧压力系数敏感性分析
各接头弯矩传递系数在各个埋深条件下随侧压力系数增加(0.4、0.5、0.6、0.7、0.8)变化规律如图 10所示。
从图10可以看出: 管片覆土小于等于5 m时,2号接头和3号接头弯矩传递系数随侧压力系数的增加分别呈二次曲线增长和下降趋势; 当埋深大于5 m时,两者随侧压力系数的增加分别表现为线性增长和下降趋势。而其余接头(1号、4号、5号和6号接头)在各个埋深下随侧压力系数的增加都表现为线性增长的趋势。分析其原因,设计地层运营阶段同埋深条件下,管片结构外荷载随侧压力系数的增加而增加,管片右拱腰位置(即3号接头位置)接头刚度与相邻管片结构刚度比也随之增大,接头弯矩传递现象趋于减弱;其余位置接头(1、2、4、5、6号)随侧压力系数增加,接头刚度与相邻管片结构刚度比随之减小,弯矩传递现象逐渐增强。从图10中还可以看出,随着覆土增加,各接头弯矩传递能力对侧压力系数的敏感程度逐渐减弱。
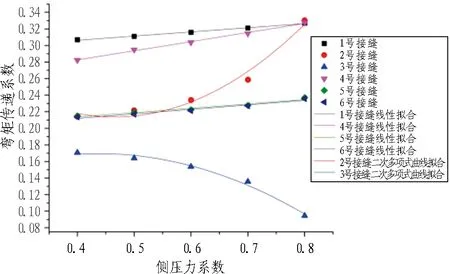
(a) 埋深为3 m

(b) 埋深为5 m
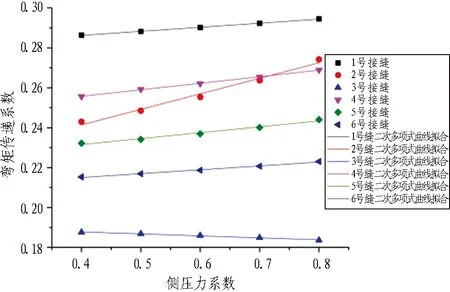
(c) 埋深为8 m
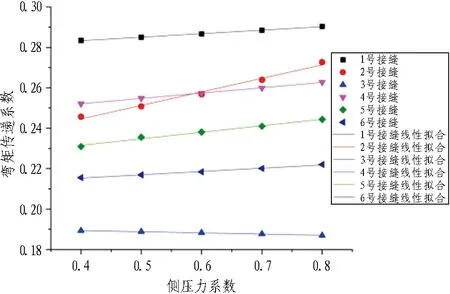
(d) 埋深为10 m
3.4弯矩传递现象描述
为客观体现异形盾构弯矩传递现象的规律,极限破坏后异形管片内外弧面裂缝的分布如图11所示。从图中可以明显地看出裂缝的规律分布特征:
1)在3环管片拱顶内弧面一定范围内(红色虚线区域)分布有较为密集的裂缝,且多为贯通裂缝,此处管片处于正弯矩较大和轴力较小的受力状态;
2)在3环管片左拱肩靠下和右拱肩靠下的外弧面位置(蓝色虚线区域)分布若干贯通裂缝,此处为管片结构负弯矩较大位置;
3)在前、后环纵缝对应的整环管片位置和整环管片纵缝所对应的前、后半环位置(绿色虚线区域)都分布有裂缝,说明纵缝所在位置附近发生了管片间明显的弯矩传递现象,使得纵缝相邻实体管片处的结构内力大于纵缝所在位置。
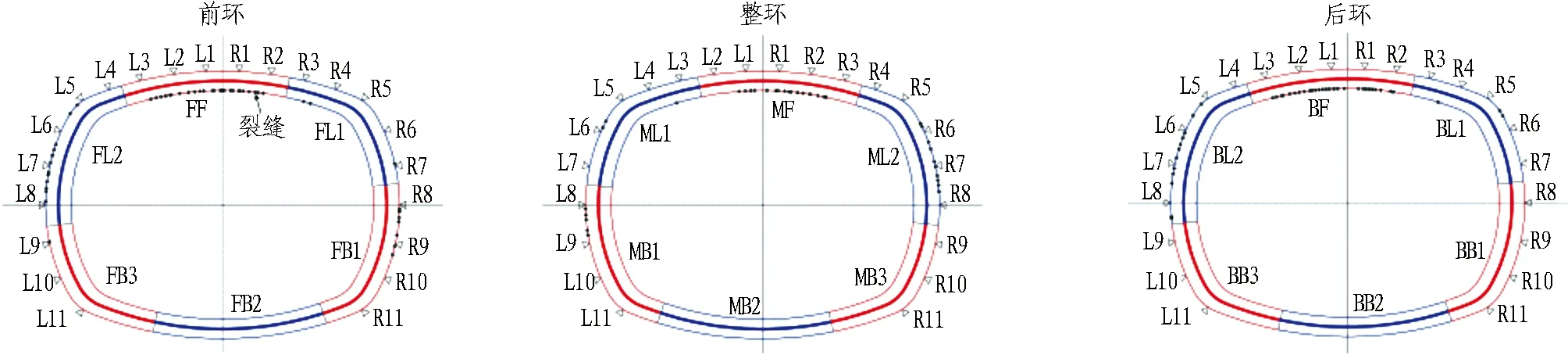
(a) 3环管片裂缝分布

(b) 内弧面

(c) 外弧面
4 结论与讨论
1)自重状态下,正弯矩区管片接头弯矩传递系数为0.099 1~0.288 2,负弯矩区为0.146 3~0.203 6;设计状态下,正弯矩区接头弯矩传递系数为0.232 8~0.315 7,负弯矩区为0.153 8~0.221 1。
2)随隧道埋深增加,当环向接头位于管片右拱肩、右拱腰和左拱脚时,接头刚度与相邻管片结构刚度比随埋深增加逐渐减小,接头弯矩传递现象趋于明显。当环向接头位于左拱肩、右拱脚和左拱腰时弯矩传递现象减弱。
3)相同埋深条件下,随侧压力系数增加,仅管片右拱腰处由于接头刚度与相邻管片结构刚度比逐渐增大而弯矩传递能力逐渐减弱,其余接头增强。随覆土增加,各接头弯矩传递能力对侧压力系数的敏感程度逐渐减弱。
4)异形盾构极限破坏工况裂缝分布规律的描述证明了异形盾构存在明显的弯矩传递现象。
5)与以往圆形隧道研究结果不同,异形盾构接头弯矩传递能力随管片结构整体刚度提高呈现出部分减弱部分提升的现象,未来将结合壳-弹簧模型等有限元方法,针对接头刚度和相邻管片结构刚度比进一步研究。
6)本文异形盾构隧道弯矩传递系数的研究可为未来异形盾构隧道的设计优化提供理论依据。
[1] 王士民, 申兴柱, 何祥凡, 等. 不同拼装方式下盾构隧道管片衬砌受力与破坏模式模型试验研究[J]. 土木工程学报, 2017, 50(6): 114.
WANG Shimin, SHEN Xingzhu, HE Xiangfan, et al.A model test for the mechanical property and failure mode of lining segments with different assembly types of shield tunnel [J]. China Civil Engineering Journal, 2017, 50(6): 114.
[2] 张建刚, 何川, 杨征. 大断面宽幅盾构管片三维内力分布分析[J]. 岩土力学, 2009, 30(7): 2058.
ZHANG Jiangang, HE Chuan, YANG Zheng. Analysis of 3D internal forces distribution of wide segment lining for large-section shield tunnel[J]. Rock and Soil Mechanics, 2009, 30(7): 2058.
[3] 钟小春, 张金荣, 秦建设, 等. 盾构隧道纵向等效弯曲刚度的简化计算模型及影响因素分析[J]. 岩土力学, 2011, 32(1): 132.
ZHONG Xiaochun, ZHANG Jinrong, QIN Jianshe, et al. Simplified calculation model for longitudinal equivalent bending stiffness of shield tunnel and its influence factors′ analysis[J]. Rock and Soil Mechanics, 2011, 32(1): 132.
[4] ARNAU O, MOLINS C. Three dimensional structural response of segmental tunnel linings[J]. Engineering Structures, 2012, 44(6): 210.
[5] KOYAMA Y. Present status and technology of shield tunneling method in Japan[J]. Tunnelling and Underground Space Technology, 2003, 18(2): 145.
[6] 沈碧伟, 丁文其, 彭益成, 等. 输水隧道管片环弯矩调整系数试验与分析[J]. 同济大学学报(自然科学版), 2011, 39(7): 994.
SHEN Biwei, DING Wenqi, PENG Yicheng, et al. Experimental study on moment adjustment factor of water-conveyance tunnel segment lining[J]. Journal of Tongji University (Natural Science), 2011, 39(7): 994.
[7] 封坤, 何川, 夏松林. 大断面盾构隧道结构横向刚度有效率的原型试验研究[J]. 岩土工程学报, 2011, 33(11): 1750.
FENG Kun, HE Chuan, XIA Songlin. Prototype tests on effective bending rigidity ratios of segmental lining structure for shield tunnel with large cross-section[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1750.
[8] 日本土木工程师协会. 日本隧道标准规范(盾构篇)及解释[M]. 朱伟, 译. 北京: 中国建筑工业出版社, 2001.
Japanese Association of Civil Engineer. Specification and explanation of tunnel (shield tunnel) [M]. Tranlator: ZHU Wei. Beijing: China Architecture & Building Press, 2001.
[9] 蒲奥.纤维混凝土管片设计研究及工程应用[D]. 成都: 西南交通大学, 2007.
PU Ao. FRC segments design research and project application[D]. Chengdu: Southwest Jiaotong University, 2007.
[10] 黄正荣, 朱伟, 梁精华. 修正惯用法管片环弯曲刚度有效率η和弯矩提高率ξ的研究[J]. 工业建筑, 2006, 36(2): 45.
HUANG Zhengrong, ZHU Wei, LIANG Jinghua. Study of effective bending rigidity ratios and moment increasing rates in modified routine method[J]. Industrial Construction, 2006, 36(2): 45.
[11] 闫治国, 彭益成, 丁文其,等. 青草沙水源地原水工程输水隧道单层衬砌管片接头荷载试验研究[J]. 岩土工程学报, 2011, 33(9): 1385.
YAN Zhiguo, PENG Yicheng, DING Wenqi, et al. Load tests on segment joints of single lining structure of shield tunnel in Qingcaosha Water Conveyance Project[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1385.
[12] 张银屏. 地面出入式盾构隧道修正惯用法计算参数研究[J]. 隧道建设, 2014, 34(2): 101.
ZHANG Yinping. Study of ground penetrating shield-bored tunnel calculation parameters in modified routine method[J]. Tunnel Construction, 2014, 34(2): 101.
[13] 地铁设计规范: GB 50157—2013 [S]. 北京: 中国建筑工业出版社, 2013.
Code for design of metro: GB 50157—2013 [S]. Beijing: China Architecture & Building Press, 2013.
[14] BOWLES J E. Foundation analysis and design [M]. New York: McGraw-Hill, 1988.
[15] Working Group No.2 of International Tunneling Association. Guidelines for the design of shield tunnel lining [J]. Tunnelling and Underground Space Technology, 2000, 15(3): 303.
PrototypeLoadingTestonBendingMomentTransferringCoefficientsofSpecialShieldTunnelswithLargeCross-section
ZHU Yeting1, 2
(1.ShanghaiTunnelEngineeringCo.,Ltd.,Shanghai200233,China;2.DepartmentofGeotechnicalEngineering,TongjiUniversity,Shanghai200092,China)
There is no relevant segment design standard for special shield tunnel due to its special cross-section. As a result, the bending moment transferring coefficients of every radial joint of special shield tunnel segment are studied based on the prototype loading tests. The results show that: 1) The overall stiffness of the special shield tunnel segment structure increases with the buried depth increase; while the bending moment transferring capacities of the joints partially increase and partially decrease due to the structural stiffness ratios between the joints and adjacent segmental structure differ with each other. 2) With the increase of the lateral pressure coefficients, the bending moment transferring capacity of all joints became weaker as the structural stiffness ratio between the joint (not including the joint located in the right arch waist) and adjacent segmental structure decrease under the same buried depth. 3) The sensitivity of the bending moment transferring capacity of each joint to the lateral pressure coefficient decreases gradually while the buried depth increase. 4) The obvious bending moment transferring phenomenon is verified by analyzing the distribution of cracks on both inner and outer surfaces of the segments after ultimate failure.
special shape; shield tunnel; large cross-section tunnel; prototype test; bending moment transferring coefficient; crack
2017-06-20;
2017-09-22
上海市国资委企业技术创新和能级提升项目(2013017)
朱叶艇(1987—),男,浙江绍兴人,2017年毕业于同济大学,隧道及地下建筑工程专业,博士,博士后,主要从事软土盾构隧道及地下工程方面的研究工作。 E-mail: 1210278theronzhu@tongji.edu.cn。
10.3973/j.issn.1672-741X.2017.10.010
U 451
A
1672-741X(2017)10-1269-07
