基于FVCOM的黄渤海潮波运动的数值模拟
2017-11-08黄学智张瑞瑾马荍沣姜英宝孙家文
黄学智,张瑞瑾,马荍沣,姜英宝, 孙家文
(1.大连海洋大学 海洋科技与环境学院,辽宁 大连 116023;2.国家海洋环境监测中心,辽宁 大连 116023)
基于FVCOM的黄渤海潮波运动的数值模拟
黄学智1,张瑞瑾1,马荍沣1,姜英宝1, 孙家文2
(1.大连海洋大学 海洋科技与环境学院,辽宁 大连 116023;2.国家海洋环境监测中心,辽宁 大连 116023)
为进一步加强黄渤海潮波数值研究,采用FVCOM海洋数值模式进行试验并对其底摩擦项进行了改进,对黄渤海的潮波运动进行了数值模拟;根据37个潮位站和3个海域海流的实测资料,对比了调和常数、潮位和潮流数据,计算结果均与实测结果吻合良好;通过对计算结果进行准调和分析,绘制了黄渤海的潮汐潮流同潮图、潮汐潮流性质分布图、潮流椭圆图和潮致余流图。结果表明:模拟区域存在4个无潮点和8个圆流点;潮汐主要以半日潮汐为主,全日潮汐分布在秦皇岛外海、海州湾外海和老黄河口近海;潮流主要以半日潮流为主,全日潮流分布在渤海海峡东南部,近岸表现为往复流,外海表现为旋转流。
黄渤海;潮波运动;FVCOM;数值模拟
潮流场对定量研究海洋的物理过程具有重要的意义。随着计算机技术和数值计算方法的发展,海洋数值模式在海洋运动研究中已经取得了较多成果。沈育疆[1]首次发表了关于东中国海的潮汐数值模拟成果,引导了国内对东中国海潮波运动数值研究的深入和发展;赵保仁等[2]在球坐标系下对东中国海海区的半日潮、全日潮的潮汐潮流进行数值模拟,其网格剖分在当时属最为精细,计算精度也相对较高。进入21世纪后,对东中国海潮波运动的研究报道较多。鲍献文等[3]、程殿忠[4]使用POM (Princeton Ocean Model)对东中国海的潮波进行了研究。张衡等[5]利用基于球面坐标系的ECOM(Estuary,Coast and Ocean Model)模式,模拟了东、黄、渤海8个主要分潮。朱学明[6]采用FVCOM(Finite Volume Coast and Ocean Model)模拟中国近海的潮波运动。葛建忠[7]和Chen等[8]利用FVCOM-ECS(The East China Sea unstructured grid Finite-Volume Community Ocean Model)东中国海模式,采用非结构嵌套网格模拟了东中国海的潮汐潮流、温盐、洋流,并对数据质量进行控制,取得了较好的效果。近年来,伴随方法在潮波模拟中取得了较好的成果,Zhang等[9]、吕咸青等[10]使用伴随法反演海底摩擦和开边界条件,提高了东中国海潮波的数值模拟精度。FVCOM(Finite-Volume Community Ocean Model)海洋数值模式,是由陈长胜教授为首的马萨诸塞州立大学海洋生态系统实验室(UMASSD)和伍兹霍尔海洋研究所(WHOI)联合开发的,该模式基于有限体积法的非结构网格、自由表面和三维原始方程[11]。本研究中,对FVCOM源代码中底摩擦项进行了改进,经过多次数值试验取得了较好的模拟效果,利用无结构化的三角形网格对黄渤海近岸复杂地形进行局部加密,详细分析了黄渤海潮汐、潮流的性质特征,旨在为黄渤海潮波运动研究提供参考。
1 模式建立
1.1模型简介
本研究中采用的是基于有限体积法的海洋数值模式FVCOM,它具有有限差分法计算高效、离散结构简单和有限元法几何灵活性的优点,既能拟合复杂的陆地边界,又能保证计算效率,在河口近岸海域的数值模拟中具有一定的优势。不规则的底部边界采用σ垂直变换来体现;水平和垂直方向分别使用Smagrinsky湍闭合模型和Mellor-Yamada 2.5阶紊闭合模型,使模型在数学和物理上闭合;该模式采用时间分裂算法,二维外模使用较短的时间步长,三维内模使用较长的时间步长,以节省计算时间;潮汐动边界采用干湿判断法来处理,能更好地保证干湿淹没地区计算的守恒性[12]。
1.2潮流模型
FVCOM模式采用σ垂向坐标,坐标变换如下:
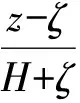
(1)
其中:H为静水深;ζ为自由表面的高度;D为总水深。
σ坐标系下,三维内模控制方程为

(2)

(3)

(4)

(5)

(6)
ρ=ρ(T,S)。
(7)
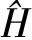
边界条件为:
自由表面边界条件,在自由海面上,σ=0:
(8)
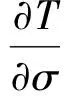
(9)
(10)
海底边界条件,在海底边界上,σ=-1:
(11)
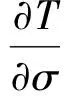
(12)
(13)
其中:τsx、τsy为海表面剪切应力;τbx、τby为海底摩擦力;uτs、uτb分别为海表面和海底对边界层的摩擦力;Qn(x,y,t)为海表净热通量;SW(x,y,0,t)为海表短波辐射通量;cp为海水的比热系数;q、l分别为湍流动能和湍流尺度。
闭合边界条件:
闭合边界即陆地边界,法向速度和通量为0:

(14)
1.3模型配置
模型计算区域为117.57°~126.91°E,36.15°~40.94°N,包括渤海和北纬36.15°以北的黄海海区,研究区域和验证点分布如图1所示。水深数据来自ETOPO1卫星数据,近岸地区使用中国航海保证部出版的海图和实测水深进行调整;模型采用非结构三角形网格,开边界空间分辨率约为0.05°,岸线空间分辨率约为0.01°,如图2所示,垂向上设为5个σ层。模型外模时间步长为1 s,内外模之比为10,底摩擦使用空间变化的底拖曳力系数来描述;本研究中只有一条开边界,即36.15°N纬线。采用潮位控制,计算时给定开边界上不同节点处的潮位值;节点处的潮位值通过中国海洋大学开发的ChinaTide潮汐预报软件取得,而流速的初始场难以确定,因此,从静水状态开始计算一般经过4~5个潮周期流场即可到达稳定状态。
潮汐预报软件ChinaTide可以在给定计算点的经纬度及时间区间情况下,通过潮汐模型得到潮位过程。此模型可以考虑Q1、P1、O1、K1、N2、M2、S2、K2和Sa等9个主要分潮,其中Sa分潮为天文气象分潮。通过插值和数值计算,可获得计算域内所有网格点上9个分潮的调和常数。利用这些调和常数,通过内插,可按下式进行海域内任意点的潮汐预报,即
系统中激光由半导体激光器产生,经由Y波导等分、调制后沿顺时针与逆时针分别进入光波导谐振腔,Y 波导的两路调制信号为不同频率的正弦波,光波经由波导腔后由光电探测器转换为电压信号,分别进入两路锁相放大器进行同步解调,解调信号其中一路作为误差信号由电流伺服回路将激光器中心频率谐锁定在谐振频率上,并由温度伺服回路进行谐振谱漂移的跟踪锁定;另一路解调信号则与前一路信号闭环后作为陀螺输出。其中正弦信号的产生、锁相放大器、后续数据处理等均由FPGA完成,并且与光电探测器等外围电路集成于一块电路板上。

图1 验证点的空间分布Fig.1 Distribution of validated stations

图2 计算海区水平网格分布图Fig.2 Horizontal mesh distribution of the simulation sea area
其中:η为潮位;hi、gi为第i个分潮的调和常数;σi为分潮角速度;t为时间;fi为分潮的交点因子;v0i为分潮的天文初位相;ui为分潮的交点订正角。
底摩擦项改进:FVCOM的底拖曳力系数Cd的表达式为
(15)
其中:k=0.4,为卡门常数;z0为海底粗糙高度,其值与床面泥沙粒径、级配和床面几何形状相关。因此,Cd是与水深和底质类型相关的参数。对于不同底质的海床,Cd值相差较大,对于淤泥质海床,Cd远小于0.002 5,这种情况下使用式(15)来计算Cd显然不合适。因此,本研究中借鉴丹麦水力研究所开发的MIKE软件中描述底摩擦的方式来描述,即通过修改源代码,使用空间变化的底拖曳力系数来描述底摩擦。具体公式为

(16)
z0=mks,
(17)
(18)
其中:m为常数,一般取值为1/30;Cf为底拖曳力系数;ks为底部粗糙高度;z0为海床粗糙尺度;Δzb为最底部水层厚度;M为曼宁系数,曼宁系数越大,底摩阻越小,反之底摩阻越大。通过计算空间变化的曼宁系数,使用式(16)~(18)来计算底拖曳力系数Cf。
2 模型验证
2.1潮位验证
调和分析时间序列长度要大于18.6年才能把所有的分潮分离,因此,本研究中采用的是准调和分析方法。模式计算时间为2015年4月15日0时—6月15日0时,使用T_TIDE[13]对后60 d的潮位计算结果进行准调和分析,得到计算区域37个潮位站4个主要分潮的调和常数,采用绝对平均误差和相关性分析来描述调和常数的吻合程度,结果见表1。M2、S2、K1和O1分潮振幅的计算结果和实测结果非常接近,4个分潮的迟角和实测结果也比较接近。

表1 M2、S2、K1、O1 4个分潮模拟结果检验Tab.1 Model validation for tidal constituents M2,S2,K1and O1
2.2潮流验证
潮流验证资料来自实测海流资料,分别为辽宁省的葫芦岛止锚湾(图3-A、B)、营口白沙湾(图3-C、D)、庄河黑岛(图3-E、F)的潮流数据。采用垂向平均实测数据和模型中层计算结果进行对比,结果见图3。从整体上来看,流速的计算结果和实测结果比较吻合,流向的计算结果整体上能反映真实的潮流涨落情况。造成偏差的原因主要是海流观测点主要位于近岸海区,模型中近岸海区水深可能不够准确、地形刻画不够精细。因此,可以认为模型的计算结果比较可靠,可为后续模型提供水动力条件。
3 潮波分析
3.1潮汐同潮图
对潮位计算结果进行准调和分析,得到计算区域所有三角形顶点的潮汐调和常数,绘制黄渤海M2、S2、K1和O14个分潮的潮汐同潮图(图4)。来自太平洋的半日潮波进入黄海后会向北传播,由于水深变浅,传播速度开始变慢,在地转偏向力、海岸线和海底地形的相互作用下,形成了整个计算区域的半日潮波系统。M2、S2半日分潮在计算区域内形成了3个无潮点,其中2个比较明显的点分别位于秦皇岛外海和威海附近海域,较不明显的一个点位于老黄河口位置,由于填海造陆等人类活动的影响,导致海岸线急剧变化,从而影响了潮流的运动,导致该无潮点已快退化到陆地上。通过与朱学明[6]的研究对比可发现,M2分潮的振幅和迟角的走向基本一致,S2振幅的走向也基本一致,而由于地形不同,与朱学明的研究相比,S2的迟角走向在黄海中部和辽东湾南部稍有偏差。全日分潮的波长比较长,仅在计算区域内形成一个逆时针旋转的潮波系统。本研究与张衡等[5]的研究成果相比,O1分潮振幅迟角大致吻合,而K1分潮振幅比较吻合,迟角存在略小偏差。
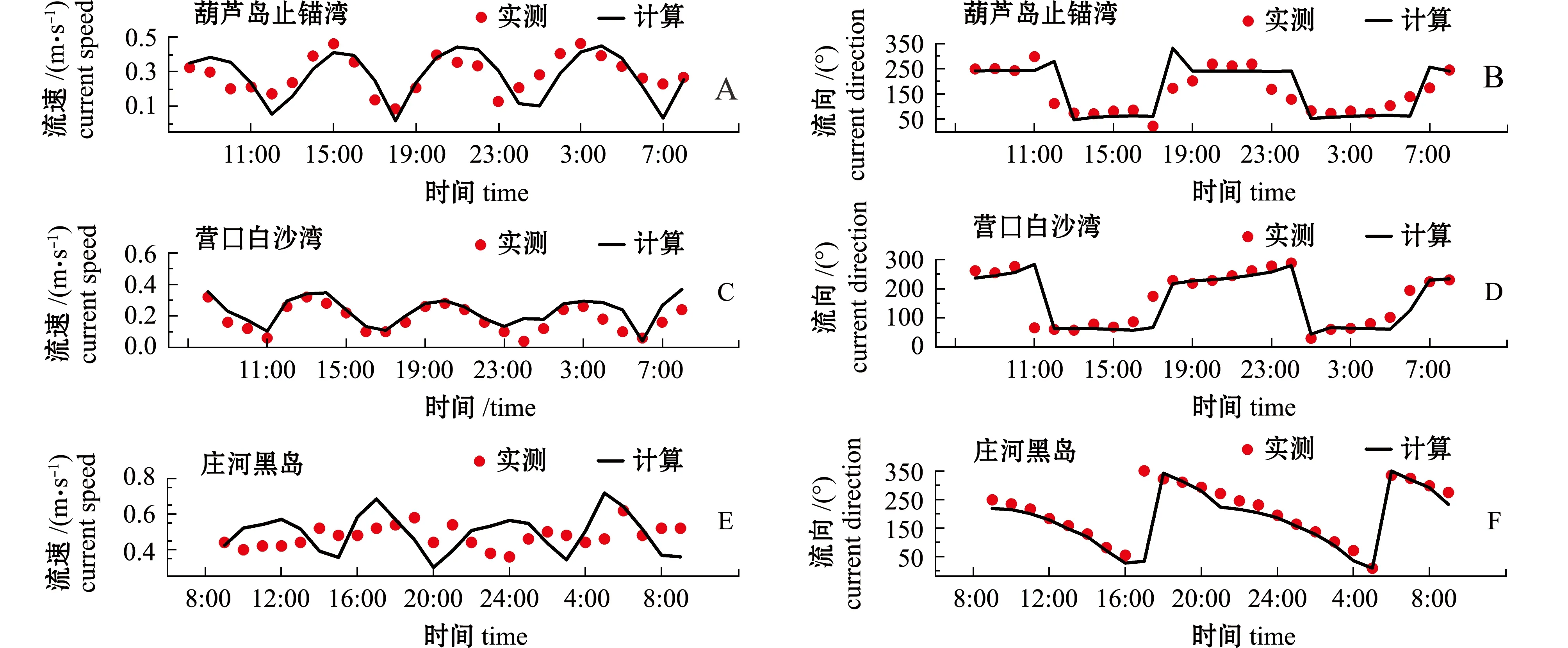
图3 潮流验证Fig.3 Verification of tidal current
3.2潮流同潮图
对潮流计算结果进行准调和分析得到黄渤海海域的潮流同潮图(图5)。潮流的强流区主要分布在朝鲜半岛西部、丹东海域、辽东湾、渤海海峡和天津港海域。其中,M2分潮流的最大流速可达1.2 m/s以上,主要位于朝鲜半岛西部海域,原因是该海域地形变化比较剧烈,海水的传播受到海底地形的影响而加快;S2分潮的最大流速可达0.4 m/s以上,和M2分潮一样,同样位于朝鲜半岛西部海域;对于全日潮流,K1和O1分潮流的强流区和半日分潮强流区分布基本一致。半日分潮流的弱流区主要分布在烟台外海和莱州湾海域,M2分潮流的流速小于0.2 m/s,S2分潮流的流速小于0.1 m/s;而全日分潮流除了在强流区较大外,其他海区均较小。从潮流的同潮时线分布可知,该海域存在4个半日潮流圆流点和4个全日潮流圆流点。本研究中潮流计算结果和相关学者的研究结果基本一致。
3.3潮汐潮流性质
黄渤海属于半日潮占优的海区,潮汐和潮流性质均采用潮型数来判断。从图6可见:渤海大部分海域属于不规则半日潮,在渤海海峡及烟台附近海域潮汐属于规则半日潮类型,而在秦皇岛近海的半日潮无潮点附近,有一小范围的规则全日潮区,在黄河口外海的半日潮无潮点周围有小块不规则全日潮区;黄海北部海域、獐子岛以北海域和青岛外海至朝鲜西部海域主要表现为规则半日潮,而在海州湾外的半日潮无潮点附近,有一小范围的规则全日潮区,周围由不规则全日潮包围着,其他部分主要呈现为不规则半日潮。对于潮流来说,黄海大部分海区主要表现为规则半日潮流,渤海的辽东湾、莱州湾西部为正规半日潮流,渤海中部为不规则半日潮流,烟台附近海域情况比较特殊,表现为规则全日潮流和不规则全日潮流,表现出与潮汐性质分布不一样的特征。
3.4潮流椭圆
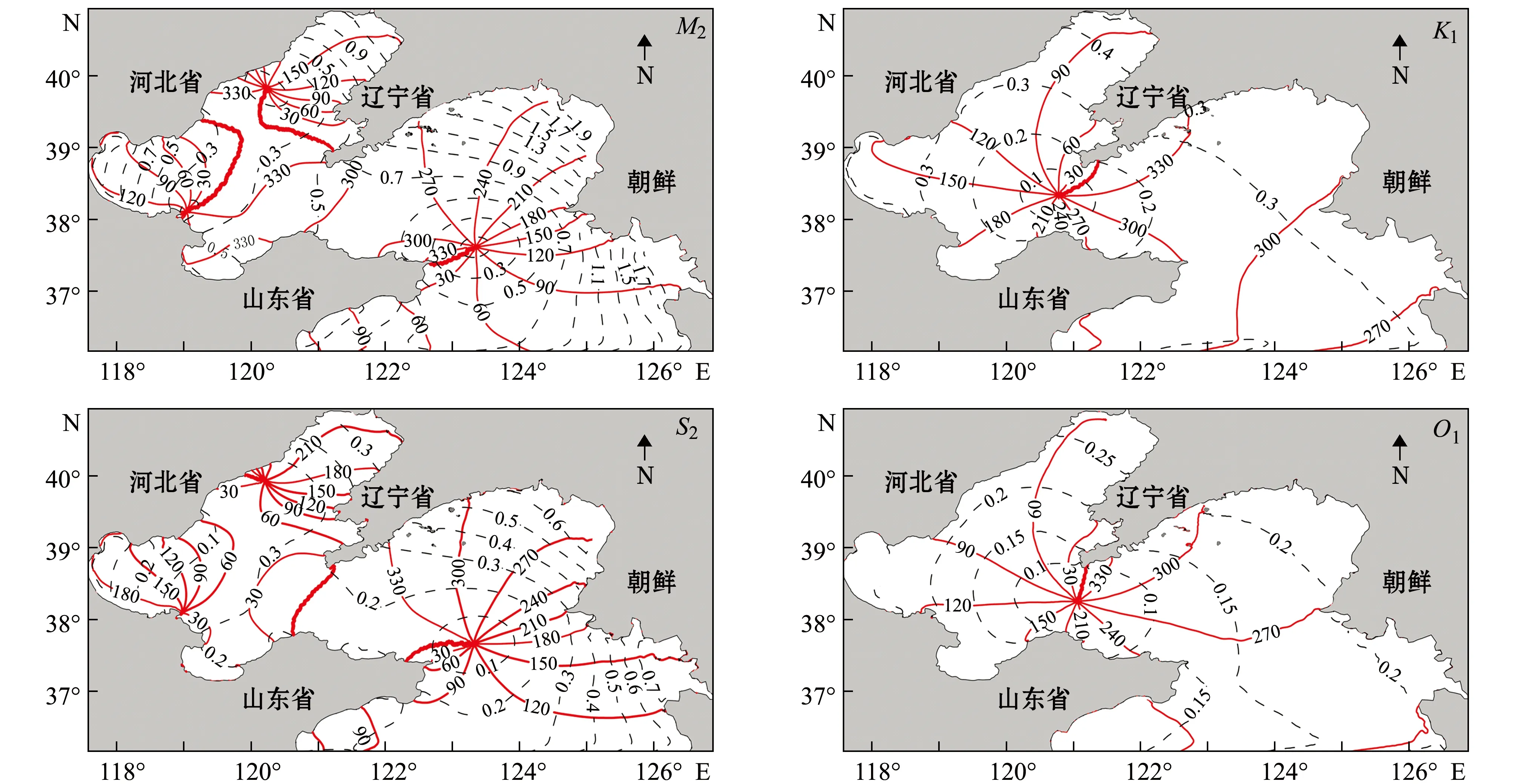
图4 M2、S2、K1、O1 4个分潮的潮汐同潮图Fig.4 Tide co-tidal charts of M2,S2,K1 and O1

图5 M2、S2、K1、O1 4个分潮的潮流同潮图Fig.5 Current co-tidal charts of tidal constituents M2,S2,K1 and O1
3.5潮致余流
本研究中探究的是潮致余流,未考虑风和径流的非线性作用。
图8给出了海洋表层的潮致欧拉余流,中层和底层的余流与表层相似,不再具体显示。从整体上看,余流大小自表层向底层方向逐次减小。外海开阔海域余流普遍较小,近岸和岛群等地形比较复杂的海域余流强度较大,对物质的运输过程起着重要的影响。造成这种现象的原因是复杂地形会导致潮流的非线性作用比较强烈,而余流表征的是潮流的非线性成分,余流的形成与地形的复杂程度有着较重要的关系。
从细节上看,余流较强的海区主要集中在獐子岛附近岛群海域、辽东湾海域、老铁山口、天津附近海域、朝鲜半岛西部海域,这些海域的余流强大,可达到20 cm/s;而外海海区余流不强,只有2~3 cm/s。中层和底层余流的分布和表层类似。
3.6无潮点
已有的研究结果给出了黄渤海区域的无潮点大致位置信息,现将本研究中模拟出的无潮点位置与其进行对比(表2)。由于M2和S2的位置大体一致,K1和O1的位置基本一致,因此,表中只给出了M2和K1无潮点的位置信息。可以看出,本研究中模拟出来的无潮点位置跟沈育疆[1]、Fang等[14]和朱学明[6]研究中的位置基本一致。其中研究海域有3个半日分潮无潮点和1个全日分潮无潮点,半日分潮无潮点分别位于秦皇岛外海、海州湾外海和一个已经快退化的位于老黄河口的无潮点,全日分潮无潮点位于烟台附近海域,4个无潮点构成的潮波旋转系统的旋转方向均是逆时针旋转,这4个旋转潮波系统构成了研究海域的潮波系统。

表2 无潮点位置和已有研究结果的对比Tab.2 Position of amphidromic points compared to predecessors
3.7圆流点
圆流点是分潮流同潮时线的交汇点,它是潮流分布的一个重要特征,圆流点处的合成潮流恒为常值,不存在最大潮流发生时间。赵保仁等[2]、李培良[15]对中国海的圆流点已做过相关研究,其对圆流点的研究主要是M2分潮,本研究中预测出来的圆流点位置同上述研究结果基本相符(表3)。位于滦河口外、莱州湾口和烟台威海外海的圆流点位置与已有的研究结果非常接近,而南黄海北部本研究中只模拟出了一个圆流点,其原因是本研究中潮波模型的开边界设置在北纬36°15′,造成开边界的潮流状况跟实际情况有所出入,刚好北黄海南部的圆流点位于本模型开边界附近,造成本模型的南黄海北部只模拟出了一个圆流点。

表3 M2分潮圆流点位置和前期研究结果的对比Tab.3 Position of M2 tidal constituent current-amphidromic points compared to predecessors

图6 计算区域的潮汐、潮流性质分布Fig.6 Distribution of tide and current property

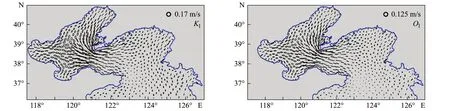
图7 M2、S2、K1、O1 4个分潮的潮流椭圆Fig.7 Current ellipse of tital constituents M2,S2,K1 and O1

图8 表层潮致欧拉余流场Fig.8 Euler residual current of surface layer in a tide
4 结论
本研究中基于改进的FVCOM,数值模拟了黄渤海海区的潮波。得出结论如下:
(1) 采用改进底摩擦项的FVCOM后,对潮位和潮流振幅的计算结果与实测值吻合良好。
(2) 研究区域的潮汐主要以半日潮汐为主,全日潮汐主要位于秦皇岛外海、海州湾外海和老黄河口近海。4个分潮的最大振幅分别可以达到2.2、0.9、0.5、0.3 m,主要位于朝鲜半岛西部海域。
(3) 研究区域的潮流以半日潮流为主,全日潮流海区位于烟台附近海域。其中M2分潮流在朝鲜半岛西部海域,振幅可达到1.2 m/s,辽东湾海域可达到0.7 m/s,丹东附近海域可达到0.8 m/s以上。其他3个分潮流的分布情况和M2分潮基本一致,只是量级稍小。
(4) 依据研究区域的潮流椭圆图可以看出,研究区域在近岸海区表现为往复流,在外海表现为旋转流。潮流椭圆潮流振幅的分布情况与潮流同潮图的分布一致。
(5) 研究区域存在3个半日分潮无潮点和1个全日分潮无潮点。半日分潮无潮点位于秦皇岛外海、海州湾外海、老黄河口近海,全日分潮无潮点位于烟台附近海域。它们均是逆时针旋转的潮波系统。
(6) 研究区域存在4个半日潮流圆流点和4个全日潮流圆流点。
[1] 沈育疆.东中国海潮汐数值计算[J].山东海洋学院学报,1980,10(3):26-35.
[2] 赵保仁,方国洪,曹德明.渤、黄、东海潮汐潮流的数值模拟[J].海洋学报,1994,16(5):1-10.
[3] 鲍献文,林霄沛,吴德星,等.东海陆架环流季节变化的模拟与分析[J].中国海洋大学学报,1995,35(3):349-356.
[4] 程殿忠.东中国海潮汐和环流的数值模拟[D].厦门:国家海洋局第三海洋研究所,2009.
[5] 张衡,朱建荣,吴辉.东海黄海渤海8个主要分潮的数值模拟[J].华东师范大学学报:自然科学版,2005(3):71-77.
[6] 朱学明.中国近海潮汐潮流的数值模拟与研究[D].青岛:中国海洋大学,2009.
[7] 葛建忠.Multi-scale FVCOM model system for the East China sea and Changjiang estuary and its Applications[D].上海:华东师范大学,2010.
[8] Chen Changsheng,Beardsley R C,Limeburner R.The structure of the Kuroshio southwest of Kyushu:velocity,transport and potential vorticity fields[J].Deep Sea Research Part A:Oceanographic Research Papers,1992,39(2):245-268.
[9] Zhang Jicai,Zhu Jianguo,Lv Xianqing.Numerical study on the bottom friction coefficient of the Bohai,Yellow and East China Seas[J].Chinese Journal of Computational Physics,2006,23(6):731-737.
[10] 吕咸青,方国洪.渤海开边界潮汐的伴随法反演[J].海洋与湖沼,2002,33(2):113-120.
[11] Chen Changsheng,Beardsley R C,Cowles G.An unstructured grid,finite-volume coastal ocean model(FVCOM) system[J].Oceanography,2006,19(1):78-89.
[12] Chen Changsheng,Liu Hedong,Beardsley R C.An unstructured grid,finite-volume,three-dimensional,primitive equations ocean model:application to coastal ocean and estuaries[J].Journal of Atmospheric and Oceanic Technology,2003,20(1):159-186.
[13] Pawlowicz R,Beardsley B,Lentz S.Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE[J].Computers & Geosciences,2002,28(8):929-937.
[14] Fang G,Yu K,Choi B H.A three-dimensional numerical model for tides in the Bohai,Yellow and East China Seas[C]//Proceedings of International Workshop on Tides in the East Asian Marginal Seas.Korean Society of Coastal and Ocean Engineers,2000:41-52.
[15] 李培良.渤黄东海潮波同化数值模拟和潮能耗散的研究[D].青岛:中国海洋大学,2002.
NumericalsimulationoftidalwavesinBohaiSeaandYellowSeabasedonFVCOM
HUANG Xue-zhi1,ZHANG Rui-jin1,MA Qiao-feng1,JIANG Ying-bao1,SUN Jia-wen2
(1.College of Marine Science and Environment, Dalian Ocean University, Dalian 116023, China; 2.National Marine Environmental Monitoring Center,Dalian 116023, China)
To enhance the numericl research of tidal current in the East China Sea, the bottom friction in Finite-Volume Coastal Ocean Model (FVCOM) is improved and the tidal wave system of Yellow Sea and Bohai Sea is simulated. The harmonic constants, tidal elevation and tidal current are validated by observation of 37 gauge stations and 3 current stations, showing a good agreement with the observations. The co-tidal chart, current ellipse, Euler residual chart and distribution chart of tidal current property are drawn by quasi harmonic analysis. There are four amphidromic points and eight current- amphidromic points in the simulation area. The tide in model domain is mainly found to be semidiurnal tide, while the diurnal tide is observed at Qinhuangdao offshore, Haizhou Bay offshore, and coastal old Yellow River delta. The current is primarily semidiurnal current, and the diurnal current is located at southeastern Bohai strait.
Yellow Sea and Bohai Sea; tidal wave; FVCOM; numerical simulation
10.16535/j.cnki.dlhyxb.2017.05.018
2095-1388(2017)05-0617-08
P731.2
A
2017-01-07
国家自然科学基金资助项目(32302232);辽宁省教育厅优秀人才项目(LJQ2015017);辽宁省自然基金资助项目(201102018)
黄学智(1989—),男,硕士。E-mail:huangxuezhi000@163.com
张瑞瑾(1975—),女,博士,副教授。E-mail:ruijinz@dlou.edu.cn
