尾翼对高速射弹的空化与阻力特性影响分析
2017-11-08赵成功魏英杰孙铁志
赵成功, 王 聪, 魏英杰, 孙铁志
(哈尔滨工业大学 航天学院,哈尔滨 150001)
尾翼对高速射弹的空化与阻力特性影响分析
赵成功, 王 聪, 魏英杰, 孙铁志
(哈尔滨工业大学 航天学院,哈尔滨 150001)
为研究尾翼对高速射弹水下运动时流体动力特性的影响,基于简化Rayleigh-Plesset空化模型和SST湍流模型,通过求解汽水混合物的RANS方程和相间质量传输方程,建立了具有相同弹体尺寸的有尾翼和无尾翼的两种平头射弹水下高速运动多相流计算模型.在相同的初始速度下,计算并对比分析两种射弹水下高速非定常运动的空泡形态及阻力特性.计算结果表明:两种射弹模型在水下高速运动时,均能迅速形成稳定的自然超空泡,有尾翼射弹的尾翼刺入空泡壁面内,破坏空泡原有的对称圆截面,形成带有凸起的空泡壁面形态;有尾翼射弹阻力系数大于无尾翼射弹阻力系数,且有尾翼射弹的阻力系数对空化数的变化更为敏感,随着空化数的增加,有尾翼射弹的阻力系数急剧增大,尾翼改变了弹体尾部超空泡的溃灭形态,空泡溃灭于弹体尾部时均引起阻力系数的波动;有尾翼射弹的空泡量纲一的长度、直径均大于无尾翼射弹的空泡量纲一的长度、直径,且在空泡溃灭于弹体尾部时,受尾翼的影响,两种射弹的空泡量纲一的长度、直径的变化速率有所差异.
多相流;射弹;尾翼;阻力特性;空泡形态
射弹在水中高速运动时,由于绕流作用会在射弹表面附近的流场形成低压区,当低压区压力降低至水的饱和蒸汽压时,这一区域内的水会汽化成水蒸气,产生空化现象.射弹体积较小,速度较高,在水中运动时易产生超空化现象[1].处于超空泡包裹之中的射弹流体阻力急剧下降,阻力的急剧下降能够增大射弹的有效射程,使射弹着靶时能保持较大的动能余量,提高击毁效果[2].国内外学者[3-7]在射弹空泡形态、阻力特性等方面开展了一些试验及数值计算工作,针对带尾翼射弹的空化问题研究较少[8-10],南京理工大学的易文俊等[11-12]开展了带尾翼高速射弹超空泡减阻试验与数值计算.尾翼对于水下射弹稳定运动的影响比较复杂,尤其是涉及到超空泡时,尾翼对超空泡的影响改变了射弹的流体动力特性.近年来随着计算流体动力学(CFD)的快速发展,使得基于CFD的数值计算方法与试验研究方法一样成为流体动力学问题研究的主要方法.尤其对于高速射弹问题,试验极其困难[13-14],因此也常用数值方法来研究射弹问题.
针对尾翼对小尺寸水下运动体的自然超空泡形态及阻力的影响,本文设计了两种平头锥体射弹模型,一种不带尾翼,另一种带三角形尾翼,二者除尾翼之外的弹体尺寸相同.基于简化的Rayleigh-Plesset空化模型和SST湍流模型,通过求解汽水混合物的RANS方程,建立了两种射弹水下高速运动的计算模型,评价了射弹尾部结构对射弹的空化特性及阻力特性的影响,为今后进一步开展超空泡射弹结构设计和流体动力研究奠定基础.
1 数值计算方法
1.1 控制方程
控制方程包括由质量守恒定律所得的连续性方程和由动量守恒定律所得的动量方程,分别如下:
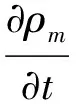
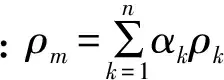
1.2 湍流模型
文中采用的是基于Baselinek-ω的添加涡黏度限制方程而得到的SST(shear stress transport)湍流模型,该模型对于逆压梯度下的流动分离问题有更精确的预测.Baselinek-ω湍流模型的控制方程为[15]:
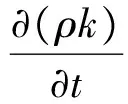
Pk-β′ρkω+Pkb,
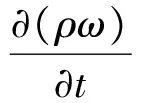
β3ρω+Pωb+2(1-F1)ρ·
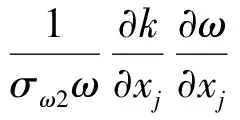
SST湍流模型中添加的涡黏度限制方程为
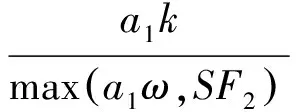
式中:μ为流体的黏性系数;μt为湍流黏度;νt=μt/ρ;F1、F2分别为混合函数;Pk、Pkb分别为湍动能中由黏性力产生的部分和由浮力产生的部分;常数β′=0.09;S为应变率的不变测度.
1.3 空化模型
描述空化流动的重要参数为空化数,表示为
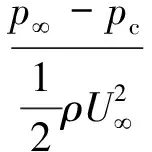
式中:p为无穷远处流场压力;pc为当前温度下水的饱和蒸汽压;为流场的参考动压力.空化数表征流场空化程度的强弱,空化数越小说明流场的空化越明显.
采用基于Rayleigh-Plesset方程的气泡流动模型来模拟流场的空泡流动.发生空化时,流场中水和水蒸汽之间的质量转换输运方程为
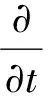
式中:Γi为进入第i相的单位体积质量源.
简化的Rayleigh-Plesset方程为
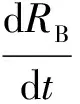
式中:p为气泡周围无扰动的流场压强;RB表示气泡的半径;pc为水的饱和蒸汽压.气体体积分数为
式中NB为单位体积内的气泡数量.气泡产生和凝结的质量转换为
式中F为经验常数.
2 射弹模型与流域网格划分
本文计算所用两种超空泡射弹的外形及尺寸如图1所示.头部直径Dn=2.5 mm,厚度为Ln=2 mm,肩部锥角为5°,弹体总长L=153 mm,弹体直径D=8.5 mm;带尾翼射弹的尾翼为三角形,翼高Hf=6.8 mm,翼长Lf=38 mm,翼厚度为3 mm,共4片沿弹体尾部周向均匀分布.
2014年3月1日,云南昆明发生严重恐怖暴力案件,社会治安面临严峻考验。谢清森坐不住了,他接连几天思考斟酌,总觉得应该也有能力为社会做点什么。
计算流域及边界条件的设置如图2所示.二者流域大小相同.坐标原点位于弹体头部中心位置,x轴与弹体轴线重合,入口边界距离射弹头部取为1.5L,侧壁边界距离弹体取为10D,弹体尾部距离出口边界取为25L.流域的侧壁和出口均采用压力开口边界条件,相对压力为101 325 Pa;计算域的参考压力设为1个标准大气压力.

图1 射弹模型
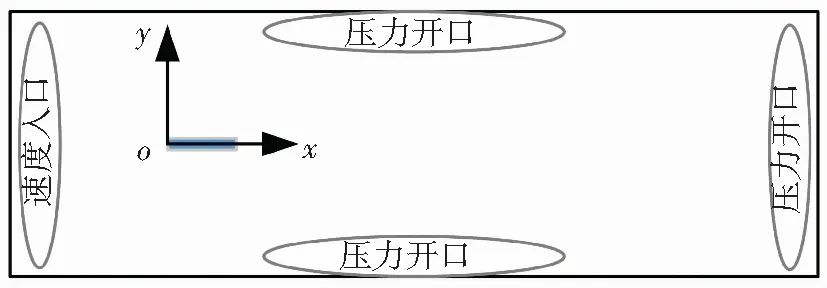
图2 计算流域及边界条件设置
计算流域及弹体附近的网格划分如图3、4所示.所采用的计算网格均为结构化六面体网格,以提高计算效率;在弹体附近进行网格加密,使得边界层的网格更精密,从而提高计算精度;计算过程中对网格的无关性进行了验证.

图3 计算流域的网格划分

图4 弹体附近的网格划分
3 结果与分析
3.1 空化特性分析
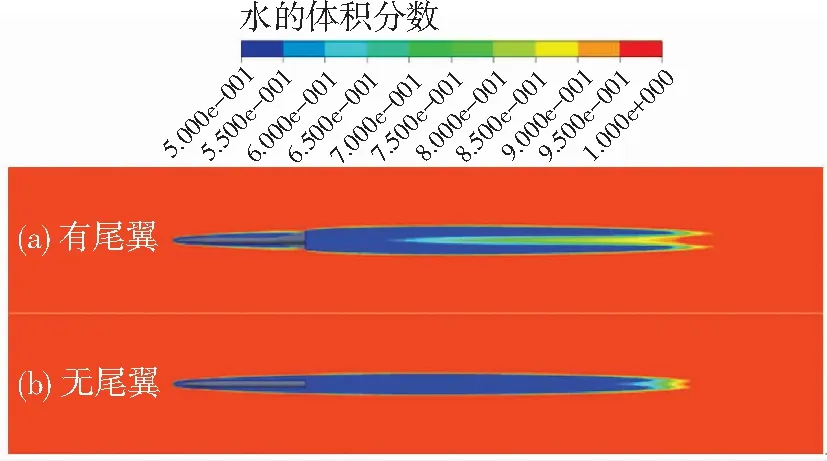
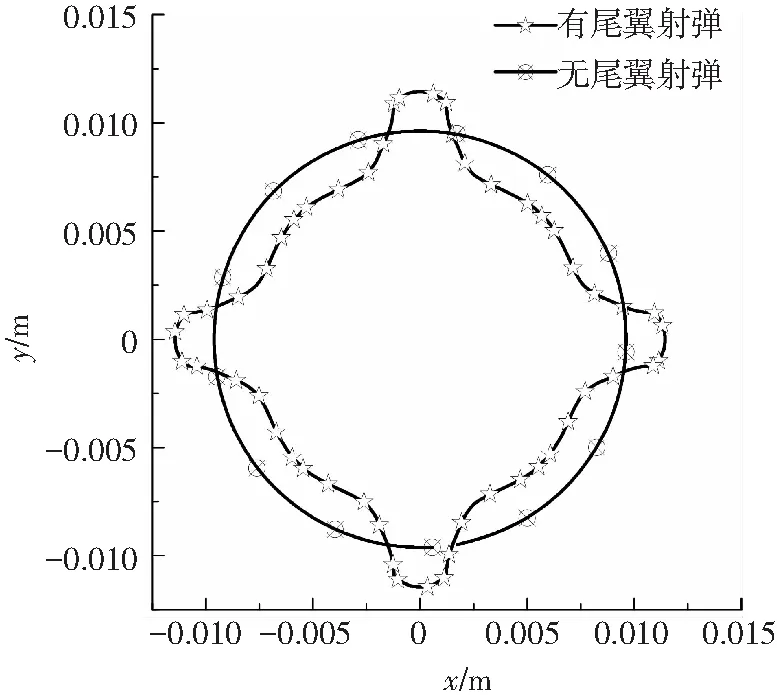
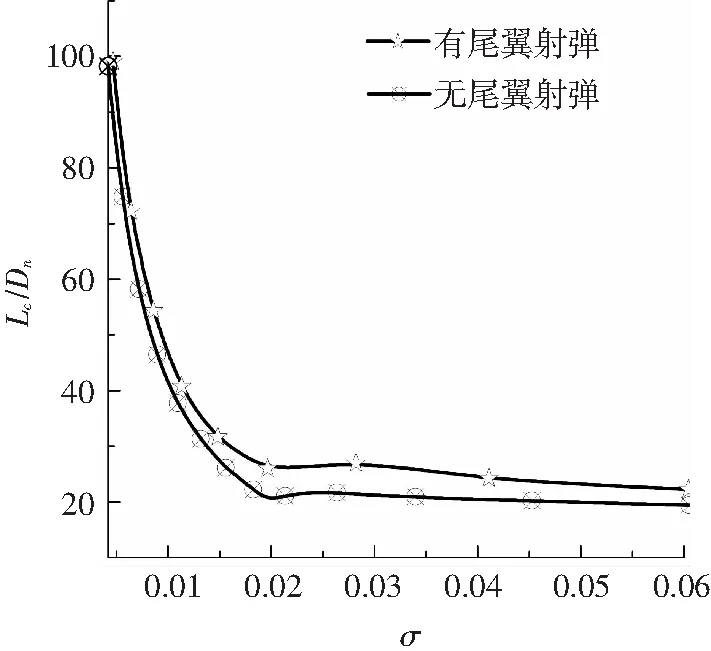
计算中给定两种射弹相同的初速度v=400 m/s,之后射弹进行自由运动,计算所得射弹的速度变化如图 5所示.
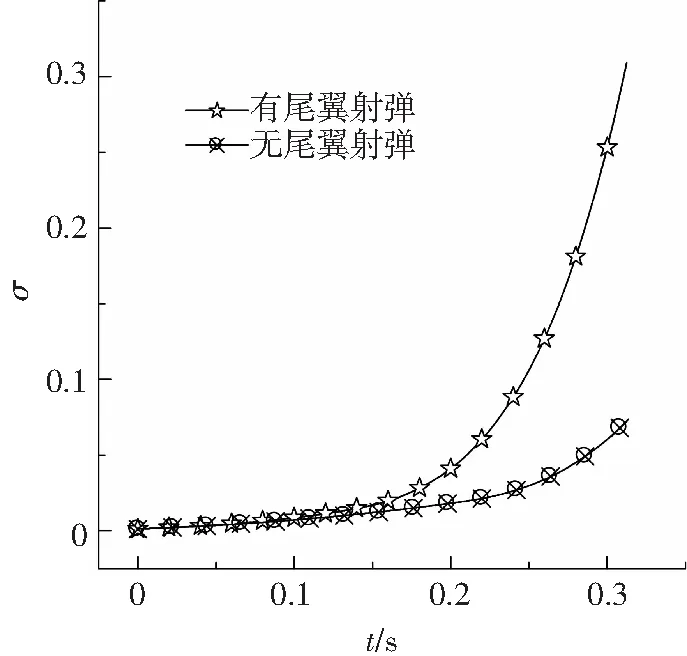
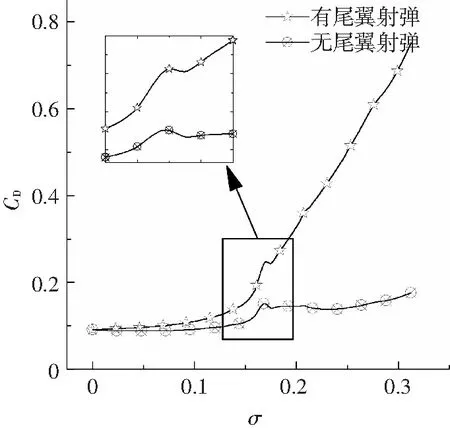
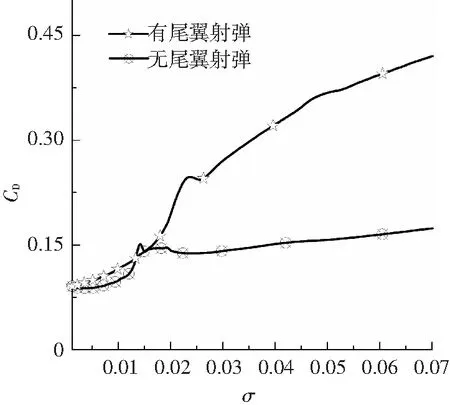
从图5中可以看出两者在初始阶段速度衰减梯度较大,而后呈减小趋势变化,两者仅在运动刚开始的t=0.05 s内速度变化较为一致,之后有尾翼射弹的速度衰减比无尾翼射弹的速度衰减较快,二者在0.2 s 空化数σ= 0.002 2(v=300 m/s)时两种射弹的超空泡形态如图7所示.图7(a)为无尾翼射弹的超空泡形态,空泡从头部边缘开始生成,基本形态为回转体,截面为圆形;图7(b)为带尾翼射弹的超空泡形态,空泡也从头部边缘开始生成,到尾翼这一段,空泡形态为回转体,截面为圆形,之后空泡光滑壁面被尾翼刺穿,致使尾翼之后的空泡截面都有4个凸起,尾翼之后的空泡与尾翼处空泡具有相似的截面图形;尾翼改变了空泡原有的轴对称形状,使得空泡壁面产生凸起,凸起的大小受尾翼刺入空泡壁面的厚度影响. 图5 射弹速度变化 图6 空化数随时间的变化 图7 空化数σ=0.002 2时两种射弹的超空泡形态 图8 空化数σ=0.002 2时两种射弹的流场相图对比 Fig.8 The contour of the water volume fraction (σ=0.002 2) 图9给出了空化数σ= 0.002 2时两种射弹尾部空泡截面对比图.由图9中可明显看出,带尾翼射弹的空泡截面在尾翼处出现与尾翼相吻合的凸起;而无尾翼射弹的空泡截面为一光滑圆形,这也说明尾翼对空泡截面有较大影响. 图9 空化数σ= 0.002 2时两种射弹尾部空泡横截面对比 Fig.9 Comparisons of profiles of cavity cross section (σ=0.002 2) 图10、11给出了两种射弹在超空泡溃灭于弹体尾部前后的空泡形态变化图.t= 0.2 s附近,两种射弹的超空泡开始溃灭于弹体尾部. 图10 无尾翼射弹超空泡形态变化 Fig.10 The cavity morphology variations of the projectile without empennages 图11 有尾翼射弹超空泡形态变化 Fig.11 The cavity morphology variations of the projectile with empennages 通常采用量纲一的长度Lc/Dn和量纲一的直径Dc/Dn来描述超空泡的几何尺寸特征,空泡直径取空泡截面上两点间距的最大值,对有尾翼射弹的空泡截面不计入凸出部分的尺寸.两种射弹的超空泡量纲一的长度与空化数的关系如图 12所示. 图12 超空泡量纲一的长度与空化数关系 Fig.12 Relations between the dimensionless length and cavitation number 由图12可知,在σ< 0.01时,二者的超空泡量纲一的长度均匀减小;在σ=0.02前后,二者的超空泡量纲一的长度差异最大;在σ=0.02附近,此时超空泡开始溃灭于弹体尾部,这时虽然两种射弹量纲一的长度都减小,但是由于尾翼存在,使得带尾翼射弹的超空泡量纲一的长度减小速率较慢.图 13给出了两种射弹的超空泡量纲一的直径与空化数的关系,从图13可以看出,在0.015<σ<0.035区间内,两种射弹的超空泡都开始溃灭于弹体尾部;有尾翼射弹的超空泡溃灭于弹体尾部时,由于尾翼的存在,使超空泡量纲一的直径明显大于无尾翼射弹的超空泡量纲一的直径. 3.2 射弹阻力特性分析 一般用阻力系数来表征射弹在水中运动所受到的阻力大小.阻力系数的大小直接影响射弹运动速度的衰减程度,进而影响射弹着靶时的剩余速度大小.阻力系数定义为 式中:FD为射弹在水中运动所受到的阻力大小,具体包括压差阻力和黏性阻力;A为射弹弹体横截面积;ρ为水的密度;U为无穷远处来流速度. 图13 超空泡量纲一的直径与空化数关系 Fig.13 Relations between the dimensionless diameter and cavitation number 图14给出了两种射弹的阻力系数随时间的变化历程. 图14 两种射弹阻力系数随时间变化历程 由图14中可以看出,带尾翼射弹的阻力系数总是比无尾翼射弹的阻力系数大.在t<0.1 s内,两种射弹的阻力系数都较小且变化幅度同样较小,此时弹体外部形成细长的完全包裹射弹的超空泡,由于带尾翼射弹的尾翼翼尖刺穿空泡壁面,因而其与水的接触面积较无尾翼射弹的接触面积较大,故其阻力系数较大;在0.15 s 图15给出了两种射弹的阻力系数与空化数的关系.对比可以发现,有尾翼射弹的阻力系数对空化数变化更为敏感,在空化数大于0.015后,随着空化数的增加,有尾翼射弹的阻力系数急剧增大,这是因为尾翼使射弹在超空泡溃灭于弹体尾部时的空泡形态不同,进而直接影响二者的阻力系数变化规律. 图15 两种射弹阻力系数与空化数的关系 1)所计算的两种射弹模型在水下高速运动时,都能迅速形成稳定的自然超空泡.有尾翼射弹的尾翼刺入空泡壁面内,破坏空泡原有的对称圆截面,形成带有凸起的空泡形态. 2)由于尾翼对空泡的影响,使得有尾翼射弹的空泡量纲一的长度、直径均大于无尾翼射弹的空泡量纲一的长度、直径,且在空泡溃灭于弹体尾部时两种射弹的空泡量纲一的长度、直径的变化速率有所差异. 3)尾翼的存在使得射弹的沾湿面积和空泡溃灭于弹体尾部时的状态与无尾翼射弹不同,相同时刻下有尾翼射弹的阻力系数大于无尾翼射弹的阻力系数,空泡溃灭在弹体尾部时均引起阻力系数的波动. [1] 孟庆昌, 张志宏, 刘巨斌, 等.水下高速航行体超空泡流动研究进展[J]. 船海工程, 2006(6):26-29. DOI: 10.3963/j.issn.1671-7953.2006.06.008. MENG Qingchang, ZHANG Zhihong, LIU Jubin, et al. Research development of high-speed super-cavitating flow of the high-speed underwater vehicle[J]. Ship & Ocean Engineering, 2006(6):26-29. DOI: 10.3963/j.issn.1671-7953.2006.06.008. [2] SAVCHENKO Y N. Control of supercavitation flow and stability of supercavitating motion of bodies[C]// Proceedings of the RTO/AVT Lectures Series on “Supercavitating Flows”. Brussels: Rto2avt and Vki, 2001:313-341. [3] 刘玉秋, 张嘉钟, 于开平, 等. 非流线型航行体超空泡减阻的实验分析和数值模拟[J]. 哈尔滨工程大学学报, 2006, 27(3) : 335-338. DOI: 10.3969/j.issn.1006-7043.2006.03.004. LIU Yuqiu, ZHANG Jiazhong, YU Kaiping, et al. Experimental analysis and numerical simulated research of the supercavitating body drag[J]. Journal of Harbin Engineering University, 2006, 27(3): 335-338. DOI: 10.3969/j.issn.1006-7043.2006.03.004. [4] 马庆鹏, 魏英杰, 王聪, 等. 锥头圆柱体高速入水空泡数值模拟[J]. 北京航空航天大学学报, 2014, 40(2):204-209. DOI:10.13700/j.bh.1001-5965.2014.02.022. MA Qingpeng, WEI Yingjie, WANG Cong, et al. Numerical simulation of high-speed water-entry cavity of cone cylinder[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2):204-209. DOI:10.13700/j.bh.1001-5965.2014.02.022. [5] 易文俊,王中原,熊天红,等. 水下射弹典型空化器的超空泡形态特性分析[J].弹道学报,2008,20(2):103-106. YI Wenjun, WANG Zhongyuan, XIONG Tianhong, et al. Analysis of supercavity shape for underwater projectile with typical cavitator[J]. Journal of Ballistics,2008,20(2):103-106. [6] LI Xiangbin, WANG Guoyu, ZHANG Mindi, et al. Structures of supercavitating multiphase flows[J]. International Journal of Thermal Sciences, 2008, 47(10):1263-1275. DOI: 10.1016/j.ijthermalsci.2007.11.010. [7] HU Chao, YANG Honglan, ZHAO Cunbao, et al. Unsteady supercavitating flow past cones[J]. Journal of Hydrodynamics, Ser. B, 2006, 18(3): 262-272. DOI: 10.1016/S1001-6058(06)60002-4. [8] SAVCHENKO Y N. Supercavitation-problems and perspectives [C]//Proceedings of the 4th International Sysmposium on Cavitation. Pasadena, CA: California Institude of Technology, 2001:1-8. [9] LOGVINOVICH G V. Some problems of supercavitating flows [C]//Proceedings of NATO-AGARD. Ukraine: NAS2IHM, 1997:36-44. [10]SARANJAM B. Experimental and numerical investigating of an unsteady supercavitating moving body[J]. Ocean Engineering, 2013, 59: 9-14. DOI: 10.1016/j.oceaneng.2012.12.021. [11]张木, 易文俊, 谭俊杰, 等. 带尾翼水下自然超空泡射弹数值模拟研究[J]. 计算力学学报, 2013, 30(1):161-165. DOI: 10.7511/jslx201301027. ZHANG Mu, YI Wenjun, TAN Junjie, et al. Numerical investigation of underwater natural supercavitating projectiles operating with the empennages[J]. Chinese Journal of Computational Mechanics, 2013, 30(1):161-165. DOI: 10.7511/jslx201301027. [12]熊天红, 张木, 易文俊, 等. 小空化数下带尾翼射弹超空泡减阻试验与数值模拟[J]. 南京理工大学学报, 2013, 37(2):244-250. DOI: 10.3969/j.issn.1005-9830.2013.02.008. XIONG Tianhong, ZHANG Mu, YI Wenjun, et al. Experimental and numerical investigation of supercavity drag reduction of wing-projectiles under small cavitation number[J]. Journal of Nanjing University of Science and Technology, 2013, 37(2): 244-250. DOI: 10.3969/j.issn.1005-9830.2013.02.008. [13]曹伟,王聪,魏英杰, 等. 自然超空泡形态特性的射弹试验研究[J]. 工程力学, 2006,23(12): 175-187. DOI: 10.3969/j.issn.1000-4750.2006.12.031. CAO Wei, WANG Cong, WEI Yingjie, et al. High-speed projectile experimental investigations on the characteristics of natural supercaviation[J]. Engineering Mechanics, 2006, 23(12): 175-187. DOI: 10.3969/j.issn.1000-4750.2006.12.031. [14]金大桥, 王聪, 魏英杰, 等. 通气超空泡水下射弹实验研究[J]. 工程力学, 2011, 28(9): 214-217, 222. JIN Daqiao, WANG Cong, WEI Yingjie, et al. Experimental study of ventilated supercavity by underwater projectile[J]. Engineering Mechanics, 2011, 28(9): 214-217, 222. [15]MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications [J]. AIAA Journal, 1994, 32(8):1598-1605. DOI: 10.2514/3.12149. Theanalysisofcavitymorphologyanddragcharacteristicsofhigh-speedunderwaterprojectilewithempennages ZHAO Chenggong, WANG Cong, WEI Yingjie, SUN Tiezhi (School of Astronautics, Harbin Institute of Technology, Harbin 150001, China) To investigate the influences of the empennages on the underwater projectile hydrodynamics, the paper established the numerical models of two high-speed supercavitating underwater projectiles which have identical dimensions except the empennages based on simplified Rayleigh-Plesset equation cavitation model and Shear Stress Transport (SST) turbulence model through solving the Reynolds Averaged Navier-Stokes (RANS) equations of mixture fluid and the mass transport equations between each phase. The projectile′s drag characteristics and supercavitation morphology variations were calculated, analyzed and compared within the identical initial velocity. The results show that the two kinds of projectile models can quickly form stable natural supercavity when moving underwater with a high speed; the impact of the empennages against the cavity surface destroys the original circle cross section of the supercavity and forms a bulge. The drag coefficient of the projectile with empennages is more sensitive to the change of the cavitation number. With the increase of the cavitation number, the drag coefficient of the projectile with empennages increases sharply, and the empennages change the collapse morphology of the supercavity near the tail of the projectile. The cavity collapse at the tail of the projectile causes the drag coefficient fluctuations. The dimensionless length and diameter of the cavity formed by the projectile with empennages are greater than those formed by the projectile without empennages. When the cavity collapses at the tail of the projectile, the variation rates of the dimensionless length and diameter of the cavity for these two projectiles are different due to the influence of empennages. multiphase flow; projectile; empennage; drag characteristics; cavity morphology 10.11918/j.issn.0367-6234.201511057 TV131.2 A 0367-6234(2017)10-0126-06 2015-11-16 中央高校基本科研业务费专项资金资助(HIT.NSRIF.201159);黑龙江省自然科学基金(A201409) 赵成功(1986—),男,博士研究生; 王 聪(1966—),男,教授,博士生导师 王 聪,alanwang@hit.edu.cn (编辑张 红)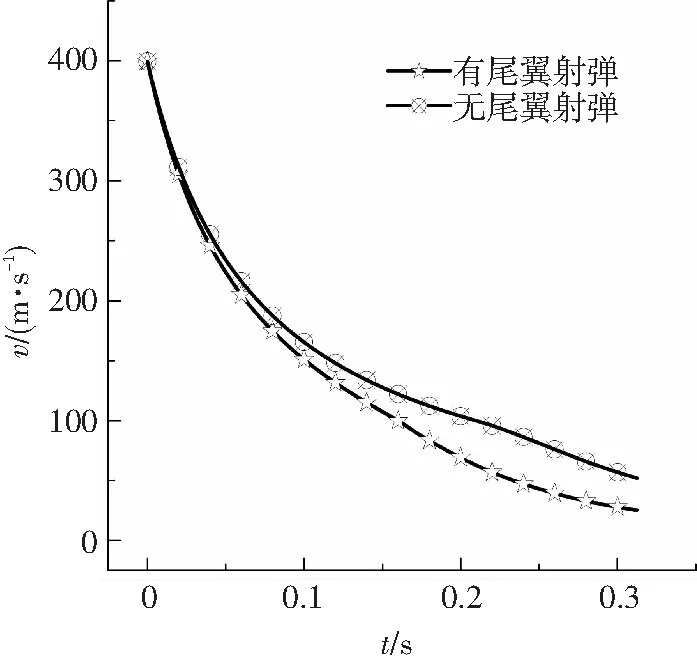



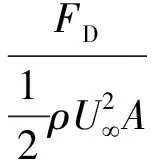

4 结 论
