新型矩形盾构接头力学性态的有限元分析
2017-11-07魏于量丁文其金跃郎龚琛杰
魏于量, 丁文其, 金跃郎, 龚琛杰, 姜 弘
(1. 同济大学土木工程学院地下建筑与工程系, 上海 200092; 2. 同济大学岩土及地下工程教育部重点实验室, 上海 200092; 3. 上海市城市建设设计研究总院, 上海 200125)
新型矩形盾构接头力学性态的有限元分析
魏于量1, 2, 丁文其1, 2, 金跃郎1, 2, 龚琛杰1, 2, 姜 弘3
(1. 同济大学土木工程学院地下建筑与工程系, 上海 200092; 2. 同济大学岩土及地下工程教育部重点实验室, 上海 200092; 3. 上海市城市建设设计研究总院, 上海 200125)
为分析评价带有接头盒的大断面矩形盾构管片接头构造和受力的合理性,基于管片纵缝接头足尺力学试验的结果,采用ABAQUS有限元软件建立该类盾构管片纵缝接头的三维精细化计算模型。通过一些分析指标,定性定量地评价在正常使用条件下各个接头的工作性态,研究正负弯矩工况下接头受力全过程的特征。结果表明: 1)正弯矩工况下的接头,弯矩-转角全过程破坏曲线呈现三折线模式,在正常使用条件下各接头均处于第2阶段,转动刚度约为100 MN·m/rad,部件均处于弹性工况,接头设计与位置选择合理; 2)负弯矩工况下的接头,弯矩-转角全过程破坏曲线呈现双折线模式,正常使用工况下各接头均处于第1阶段,转动刚度约为276 MN·m/rad,但接头受力处于2阶段的临界位置,所受负弯矩值偏大,安全储备较低,设计时应当注意。
矩形盾构管片接头; 力学性态; 三维精细化有限元模型
0 引言
伴随着预制拼装技术的不断成熟,地下结构向着大跨大断面的结构形式发展。大断面矩形盾构隧道结构具有很好的空间利用率,但其受力情况较圆形结构不利;同时接头又是所有预制拼装结构的薄弱环节,因而对矩形盾构管片接头受力的研究十分重要。此外接头盒作为一种连接预埋件,其合理的构造设计以及与混凝土共同受力机制值得研究。基于上述特征,现阶段对于矩形盾构接头构造形式的研究不多,且目前接头力学足尺试验不易开展,而数值模拟相对容易实施。采用合适的有限元模型模拟接头受力特征是解决上述问题的有效手段。
管片接头力学行为是盾构管片设计中重要的环节。从大量整环试验[1-2]、管片接头试验[3-5]以及有限元模拟[6-8],到接头理论解析解的推导[9-10],许多学者对管片接头的抗弯力学性态展开了研究,提出了一系列简化计算模型,取得了诸多研究成果。
对于重大或者新型盾构管片接头,接头的足尺力学试验仍然是最主要的研究手段。足尺力学试验不仅能真实地反映接头的力学性能,直接论证接头设计的合理性,同时也能给数值模型提供恰当的参数。其缺点在于试验耗费大,研究周期长。鉴于此,许多学者开始采用数值有限元的手段研究管片接头力学,采用非线性弹簧或者连接件,用表征管片接头刚度来简化计算,简单明确。梁-弹簧模型、壳-弹簧模型以及梁-接头模型[11-12]等均属于这一类。考虑到二维简化计算模型的非线性弹簧概念较为笼统,很难适应不同管片接头的实际构造,由此产生了采用实体单元建模的三维数值模拟。对于管片接头的抗弯性能,张鹏[13]采用ANSYS软件建立了北京地铁4号线盾构隧道管片直螺栓连接接头的三维有限元模型,通过此模型研究了轴力、螺栓位置与管片厚度对接头抗弯刚度的影响,发现螺栓位置的影响最大。张厚美等[14]采用Algor软件对装配式管片接头进行了三维有限元分析,得到了混凝土应变、接头位移、接缝转角、螺栓应力等计算结果,数值结果与试验值的变化规律相同,但数值结果有差异。
众多研究表明,管片接头构造的不同决定了力学性能的差异,前期的试验成果难以适用所有的管片接头。现阶段对于大断面矩形盾构接头力学性能研究不多,设计经验尚不足。文献[15-16]基于宁波地铁3号线,对带有中柱的类矩形盾构隧道进行了整环足尺试验与现场原位测试,研究了450 mm厚带接头盒的管片接头在不同工况下的极限承载能力与破坏机制。上述足尺试验所得到的各接头破坏模式与整环收敛变形可作为相关工程的参考;但由于它带有中柱且管片的曲度较大,故并非是严格意义上的矩形盾构。本文建立带有接头盒的大断面矩形盾构管片接头三维精细化模型,通过与试验结果的对比,论证该模型的可靠性。然后通过精细化模型的模拟,重点评价各接头在正常使用条件下的力学性能,得到管片接头的极限承载能力,依据接头的变形量与各部件的应力状态,论证分析接头构造的合理性与安全性。
1 工程背景
1.1带接头盒矩形盾构管片构造
某矩形盾构区段管片采用C60混凝土,隧道壁厚为600 mm,外包尺寸为10.3 m×8.86 m,横断面形式如图1(a)所示。管片环由8块构成,管片纵缝接头均采用预埋接头盒和4 根8.8级 M24 直螺栓连接,直螺栓呈双排上下布置,预埋铸铁接头盒通过锚筋与混凝土连接,管片接头的局部构造形式如图1(b)和1(c)所示。矩形盾构管片接头详细参数如表1所示。
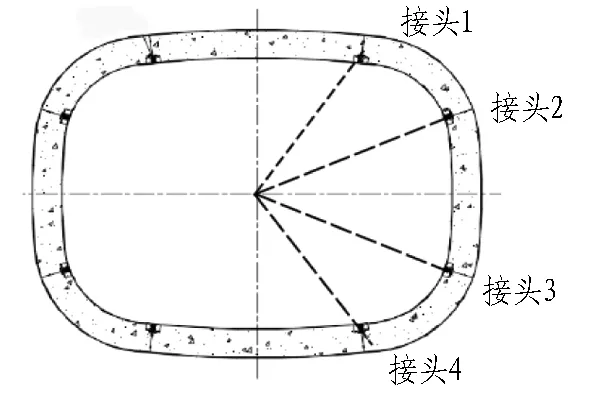
(a) 管片横断面分块图
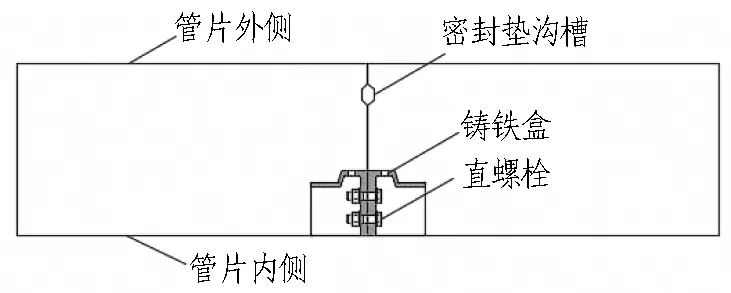
(b) 管片接头构造侧视图

(c) 管片接头构造端面图
表1矩形盾构管片接头详细参数
Table 1 Detailed parameters of rectangular shield tunnel segment joints

项目型号尺寸混凝土C601.2×0.6铸铁盒QT550-50.19×0.205×0.185螺栓8.8级高强0.12
注: 1)尺寸列单位以m计; 2)螺栓为M24型直螺栓。
1.2管片各接头内力工况
实际工程段隧道的覆土深度为9~13 m,通过对不同埋深断面的受力计算,得到了各接头最不利的内力组合。本文重点研究接头的抗弯性能,故暂不考虑剪力的影响。矩形盾构隧道管片接头内力如表2所示。
2 管片接头三维有限元精细化模型
2.1模型建立
三维精细化模型依据前期已开展的矩形盾构隧道接头足尺力学试验(见下文),由带有加载支座的2块混凝土管片构成。接头所包含各部分的单元类型见表3。铸铁接头盒通过锚筋与混凝土相连,为了简化和更容易收敛,钢筋采用三维桁架单元模拟。该模型未考虑螺栓初始预紧力以及弹性密封垫的影响,整个精细化有限元模型如图2所示。

表2 矩形盾构隧道管片接头内力

表3 接头精细化建模与单元类型

(a) 混凝土管片
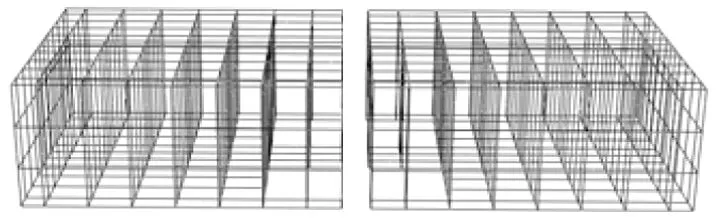
(b) 钢筋骨架
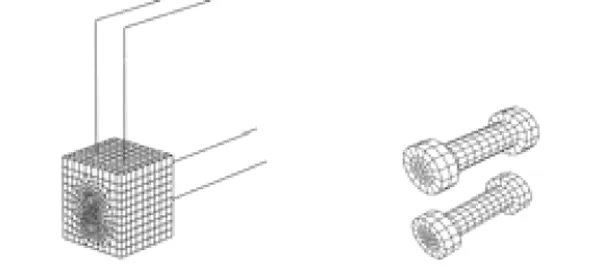
(c) 铸铁盒和锚筋 (d) 螺栓
图2管片接头三维精细化有限元模型
Fig. 2 3D fined finite element model of segment joints
2.2参数设置
对于混凝土的非线性本构关系,有文献采用弹塑性模型,该类模型参数设置简单,大多采用多折线强化或者理想弹塑性本构关系[14]。文献[17]采用混凝土塑性损伤模型,基于混凝土单向拉压曲线和定义塑性损伤因子,可以较好地反映混凝土材料拉压异性以及损伤演化与塑性滑移之间的相互作用;但是这种模型参数设置较为复杂,而且对于损伤因子的计算尚没有完全统一的计算方法[18]。文献[19]对比了这2种塑性模型的计算结果,结果表明在弹性阶段2种本构关系计算结果基本吻合,但到了塑性以及破坏阶段,塑性损伤模型可更好地模拟后期结构承载力下降的过程。从前期足尺力学试验接头全过程破坏的曲线来看,结构破坏时的下降段不明显,所以采用参数简单的弹塑性模型即可。其中C60混凝土的单向压缩关系曲线是由GB 50010—2010《混凝土结构设计规范》附录C中推荐的公式计算获得,如图3所示。此外,螺栓、锚筋以及钢筋的本构均采用弹塑性硬化模型,如图4所示。
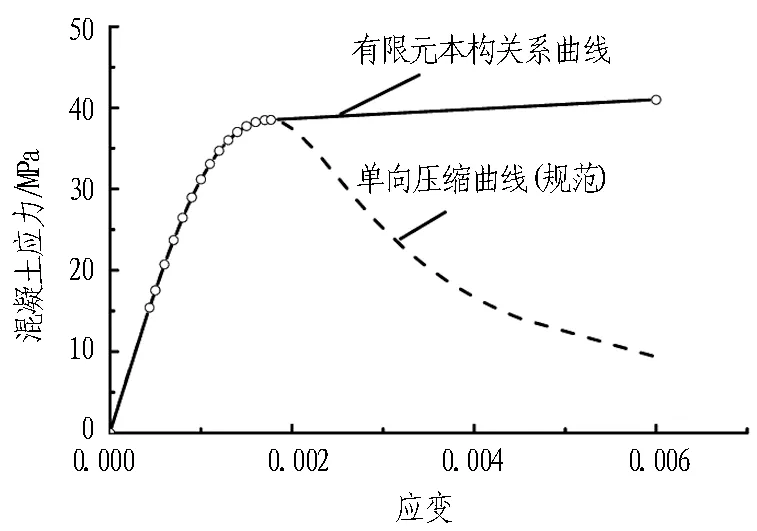
图3 有限元混凝土材料本构
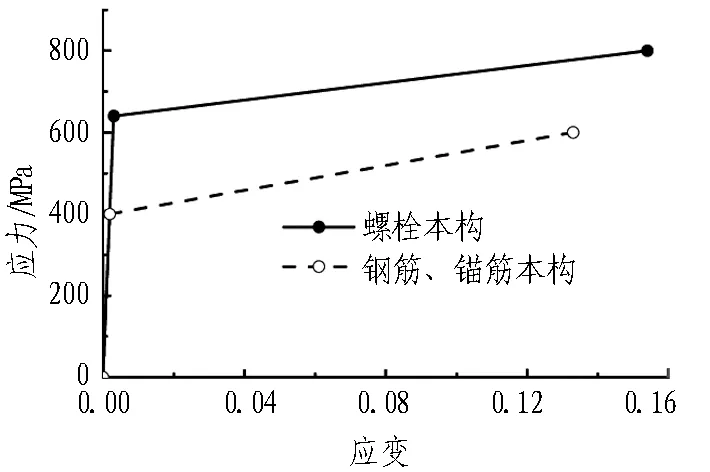
图4 有限元螺栓与钢筋材料本构
接头三维精细化有限元模型的计算结果取决于对实际接头合理的模拟与简化,其中接触情况、边界条件设置以及加载方式等尤为重要。本有限元模型的边界条件与加载方式与前期接头足尺力学加载试验一致,即将混凝土管片接头放在支座上,采用加载分配梁加载垂向荷载,如图5所示。有限元模型中各部件的接触方式如表4所示。
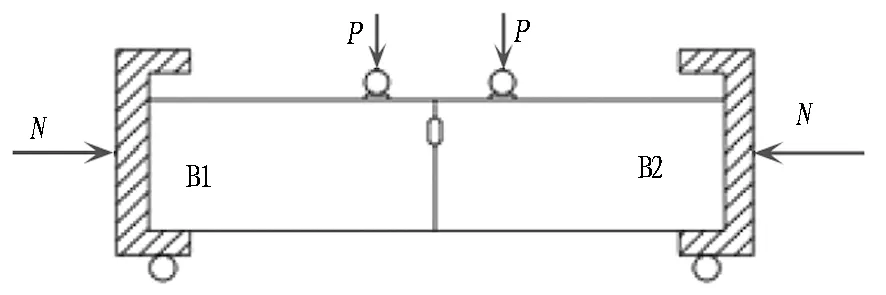
图5 矩形盾构管片接头加载与边界条件示意图Fig. 5 Sketch of loading and boundary conditions of rectangular shield tunnel segment joints
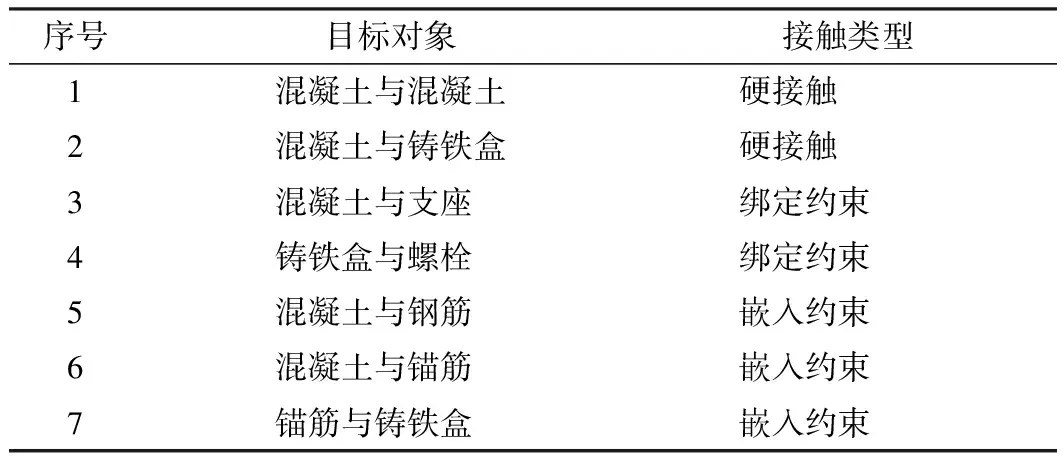
表4 模型各部件的接触方式
3 结果分析
3.1模型验证
采用同济大学自行研发的CPJ-2000管片三向加载设备,对管片接头进行了全过程抗弯破坏试验(见图6)。为了完整研究该类接头的力学特性,采用等轴力加载方式(即先施加接头轴力再施加垂向荷载),在正负弯矩工况下对管片接头进行了2组破坏试验,得到了轴力值为1 000 kN时管片接头的弯矩-转角全过程关系曲线,如图7所示。

图6 CPJ-2000管片三向加载设备示意图
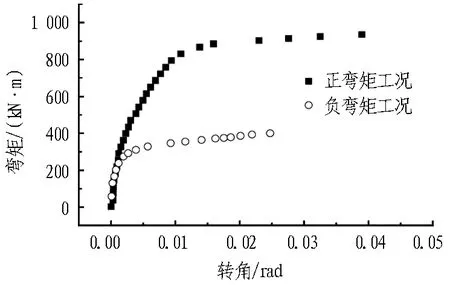
图7 管片接头足尺力学试验部分成果(N=1 000 kN)Fig. 7 Partial results of full-scale mechanical test on segment joint (N=1 000 kN)
为验证该三维精细化模型计算结果的合理性,提取轴力等于1 000 kN时有限元计算结果与足尺力学试验的数据进行比较分析。图8—10依次对比了接头破坏全过程弯矩-转角曲线、接头张开量和压缩量曲线,可以看出三维有限元模型的结果与试验结果较为吻合,表明该三维精细化有限元模型可以较好模拟接头转动张开的力学特点。
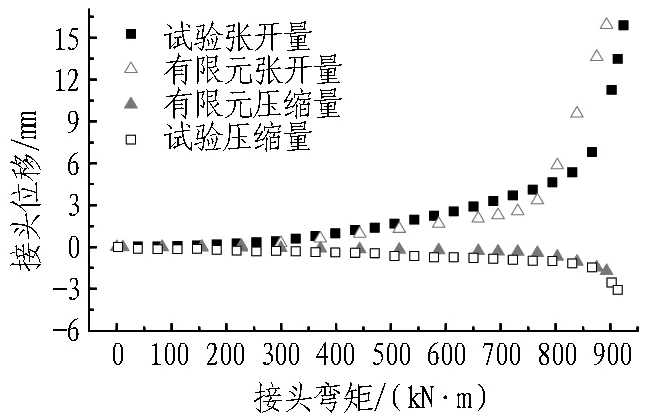
图8 正弯矩工况接头变形量对比(N=1 000 kN)Fig. 8 Comparison between FEM simulation results and test results of joint deformation under positive bending moment (N=1000 kN)
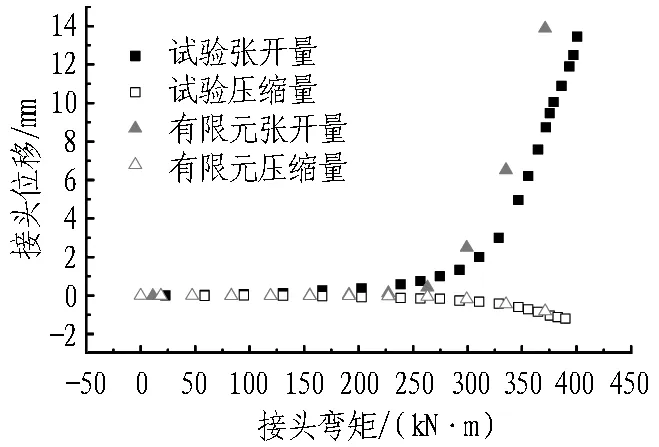
图9 负弯矩工况接头变形量对比(N=1 000 kN)Fig. 9 Comparison between FEM simulation results and test results of joint deformation under negative bending moment (N=1 000 kN)
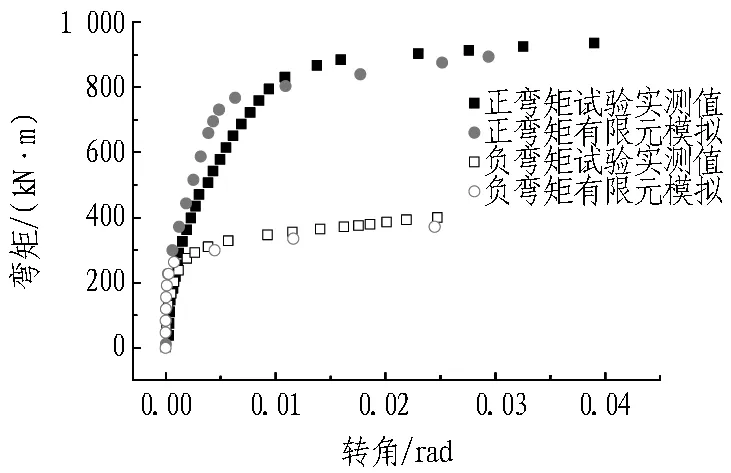
图10 接头弯矩-转角曲线对比(N=1 000 kN)Fig. 10 Comparison between FEM simulation results and test results of bending moment-rotation angle curve (N=1 000 kN)
为了验证接头构造设计的合理性与安全性,针对表2已经计算得到的各接头内力工况,采用该精细化有限元模型模拟了图1(a)4个接头的受力情况,分析评价了接头各部件的工作性态。
3.2正弯矩工况下接头抗弯力学性态
参照大量接头破坏试验,对于盾构隧道管片接头,正弯矩工况下常见的接头破坏类型主要归纳为3种:混凝土受压区压碎剥落、螺栓屈服拉断以及接头盒连接件的局部破坏。从上述的破坏形式中可以提取3种作为定性衡量接头承载力以及力学性态的指标,即受压区混凝土压应力、螺栓拉应力以及锚筋接头盒的受力状态。三大指标可以用于定性判别接头所处的受力状态,评估接头的工作性能。
接头1和接头4受到正弯矩作用,接头力学特性集中表现为外侧压缩、内侧张开。设计过程应该保证正常使用中接头的张开量、压缩量以及转角不超过限值要求,故张开量、压缩量以及转角可以作为评价接头工作性态的定量指标。
盾构管片在正弯矩设计工况(表2中的内力值)下接头1和接头4各部件的应力见图11和图12。基于3种定性判断指标,可对接头进行如下分析。
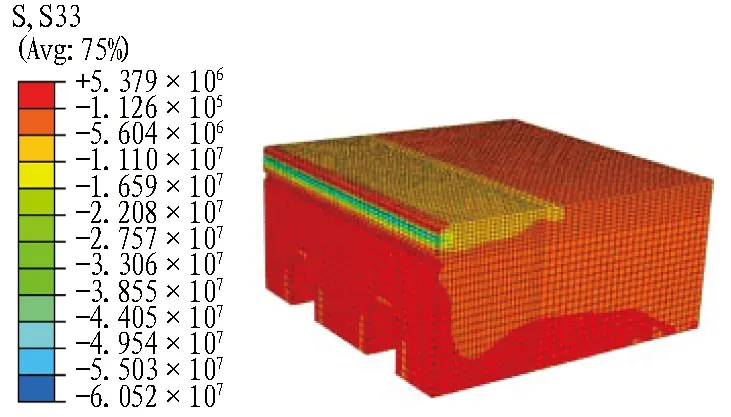
(a) 混凝土管片
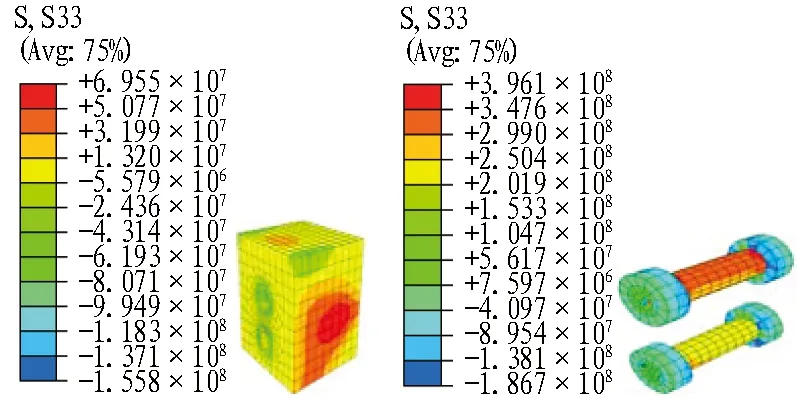
(b) 铸铁盒 (c) 螺栓
S33表示轴向应力。
图11设计工况下N=1 091.175 kN接头1各部件应力云图(单位: Pa)
Fig. 11 Stress nephograms of joint 1 under design case ofN=1 091.175 kN(unit: Pa)

(a) 混凝土管片
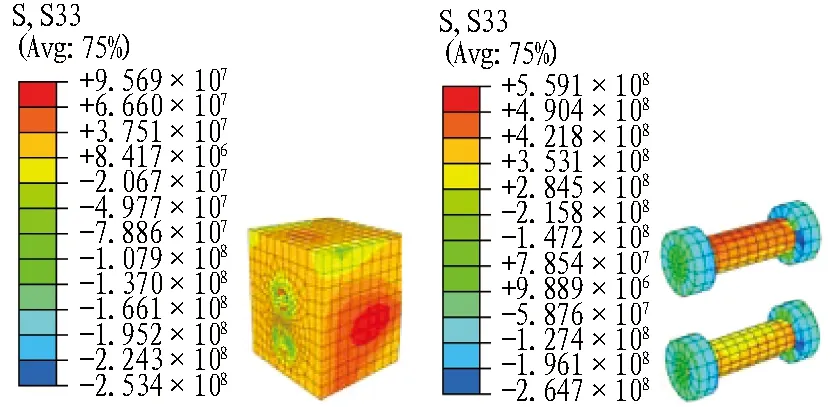
(b) 铸铁盒 (c) 螺栓
S33表示轴向应力。
图12设计工况下N=1 274.555 kN接头4各部件应力云图(单位: Pa)
Fig. 12 Stress nephograms of joint 1 under design case ofN=1 274.555 kN(unit: Pa)
1)由于构造要求,在接头顶部为30 mm的高度内,两侧混凝土各后退了2 mm,因而在混凝土受压区,2个接头均出现了局部应力集中的现象。其他部位混凝土挤压应力总体不大,故在正常使用条件下对于接头1和接头4处混凝土受压区总体工作性能良好。
2)正弯矩工况下,上下排螺栓均未达到屈服,螺栓处在弹性范围内可有效抑制接头内侧的张开量。
3)铸铁盒与锚筋均处于弹性阶段,接头预埋件工作性态良好。值得注意的是,接头盒侧壁拉应力较为明显,极有可能发生撕裂破坏。实际上,在前期矩形盾构接头足尺力学试验中的破坏阶段确实发生了如图13所示的铸铁盒侧壁撕裂现象。从有限元的应力分析结果上看,两者吻合得较好。

图13 足尺力学试验铸铁盒侧壁撕裂破坏
采用上述3个定性指标分析接头状态过于笼统,为定量评估正弯矩工况下接头的工作性态,采用三维有限元精细化模型对接头进行极限承载力计算,得到接头从弹性到塑性软化到压碎破坏全过程的关系曲线。图14显示了接头1和接头4在上述弯矩-转角全过程关系曲线上对应的位置。为了方便比较,将具体数据列于表5和表6中,表中同时列出了螺栓屈服点以及极限承载情况下的接头的弯矩值与转角值。
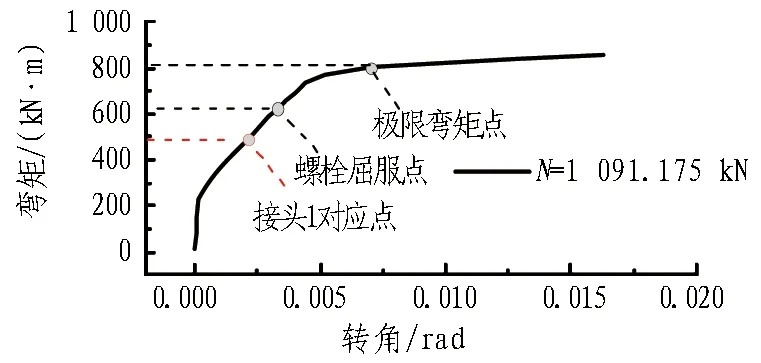
(a) 接头1(N=1 091.175 kN)
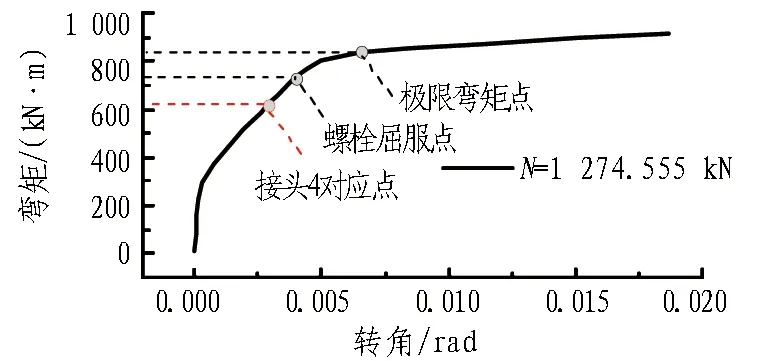
(b) 接头4(N=1 274.555 kN)
表5正弯矩工况下接头弯矩评估
Table 5 Joint bending moment assessment under positive bending moment
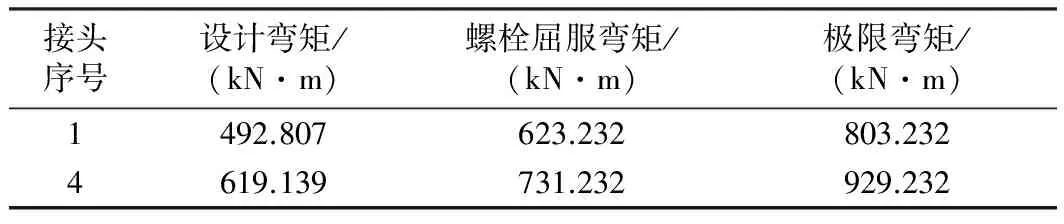
接头序号设计弯矩/(kN·m)螺栓屈服弯矩/(kN·m)极限弯矩/(kN·m)1492.807623.232803.2324619.139731.232929.232
表6正弯矩工况下接头转角评估
Table 6 Joint rotational angle assessment under positive bending moment
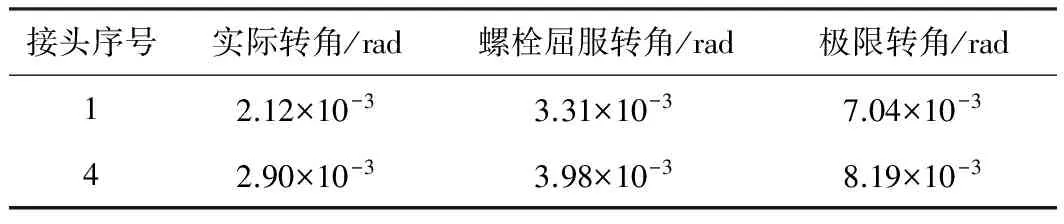
接头序号实际转角/rad螺栓屈服转角/rad极限转角/rad12.12×10-33.31×10-37.04×10-342.90×10-33.98×10-38.19×10-3
由图14可以看出: 此类带接头盒的大断面盾构隧道接头在正弯矩工况下,接头的抗弯刚度呈现明显的三折线模式。初始段的抗弯刚度很大,一般可以近似认为无限而忽略接头的转动;第2段的抗弯刚度约为100 MN·m/rad;第3阶段趋于水平,抗弯刚度约为5.5 MN·m/rad。而接头1和接头4均位于抗弯刚度曲线的第2阶段上,故正常使用工况下接头的抗弯刚度取值应该选取第2阶段。此外相比传统350 mm厚的地铁盾构管片接头,文献[20]中正常使用工况下的试验抗弯刚度约在11 MN·m/rad。由此可见, 矩形盾构管片接头的正向抗弯性能要高于地铁盾构隧道接头,其原因大致有以下3点: 1)截面高度增大,较大的管片厚度有利于提高接头正弯矩工况下的承载能力;2)采用短直螺栓代替了长直螺栓,文献[21]研究表明可以有效提高抗弯性能;3)采用铸铁预埋件可以大大减小对接头断面的刚度削弱作用。
正弯矩工况下接头的变形量如图15所示。
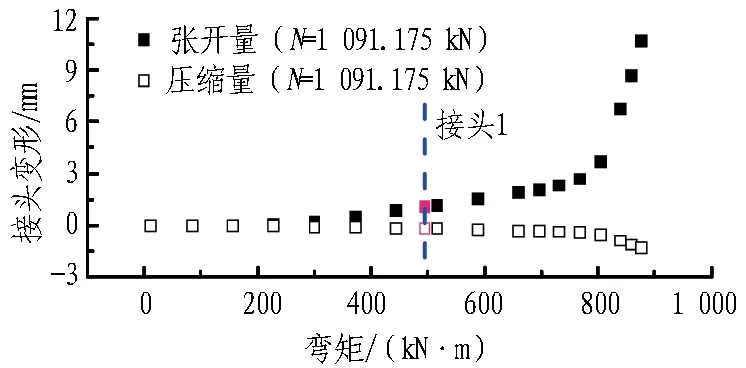
(a) 接头1张开与压缩量
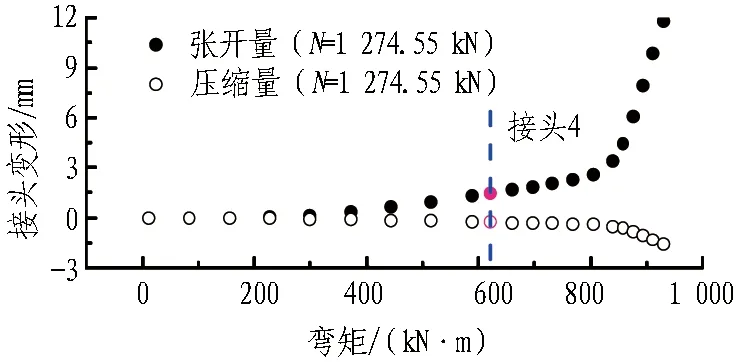
(b) 接头4张开与压缩量
对于所有盾构隧道而言,接头张开量是一个评价其工作性态的重要指标。图15蓝色虚线是接头1和接头4在接头变形量-弯矩全过程曲线上对应的位置。在正弯矩内力工况下,2接头的张开量最大约1.5 mm,不影响接头的正常受力与防水能力。
3.3负弯矩工况下接头抗弯力学行为
由于接头螺栓合力作用点偏下,同时截面高度较大,相比小断面地铁盾构隧道而言,大断面矩形盾构管片接头在负弯矩工况下的力学行为更值得关注与研究。此类接头极有可能因为较大的负弯矩导致张开量过大甚至发生破坏。接头2和接头3受负弯矩作用,力学特征集中表现为外侧张开,内侧压缩。对比表2的内力结果,接头2相比接头3更不利。管片在负弯矩设计工况下(N=1 530.097 kN,M=406.994 kN·m)接头2各部件的应力见图16。基于3种定性判断指标,可对接头进行如下分析:
1)在正常使用条件下,受压区混凝土最大压应力约22 MPa,接头2处混凝土受压区总体工作性能良好。
2)上下排螺栓均未达到屈服,螺栓仍处于弹性受力阶段。
3)铸铁盒与锚筋均处于弹性阶段,接头预埋件工作性态良好,铸铁盒侧壁受压明显。

(a) 混凝土管片
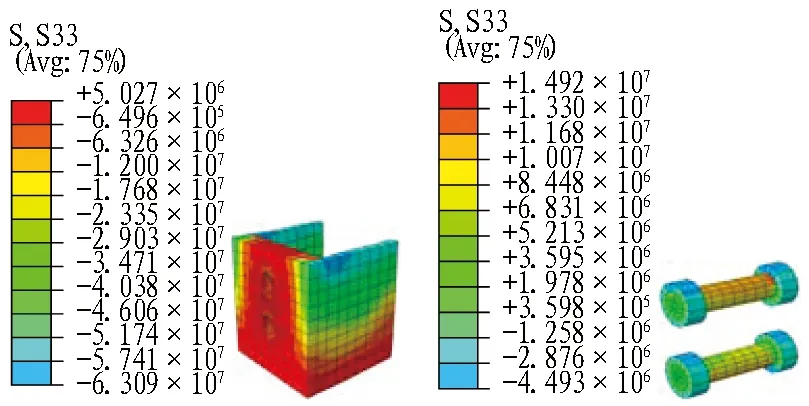
(b) 铸铁盒 (c) 螺栓
S33表示轴向应力。
图16设计工况下N=1 530.097 kN接头2各部件应力云图(单位: Pa)
Fig. 16 Stress nephograms of joint 1 under design case ofN=1 530.097 kN(unit: Pa)
接头2和接头3在接头弯矩-转角全过程曲线上的位置见图17。与正弯矩工况不同的是,抗弯刚度呈现双折线形式。主要的原因是螺栓位于截面上部,难以抑制接头的张开。当接头张开发展至螺栓位置时,螺栓迅速屈服,导致接头提前进入破坏过程。如表7和表8所示,虽然2个接头暂时处于接头转动第1阶段,然而当弯矩再略有增加时,螺栓将迅速屈服,接头变形量将突然增大(如图18所示),接头将处于破坏阶段。因而接头没有充足的安全储备,在正常使用条件下可能出现变形量过大甚至破坏等问题。
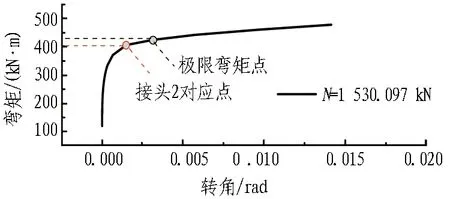
(a) 接头2(N=1 530.097 kN)
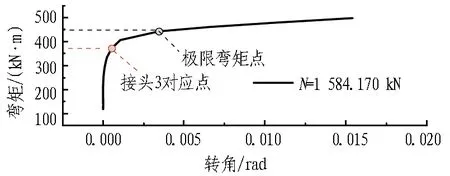
(b) 接头3(N=1 584.170 kN)
表7负弯矩工况下接头弯矩评估
Table 7 Joint moment assessment under negative bending moment

接头序号设计弯矩/(kN·m)极限弯矩/(kN·m)比值2406.994425.2321.043369.945443.2321.20
表8负弯矩工况下接头转角评估
Table 8 Joint rotational angle assessment under negative bending moment
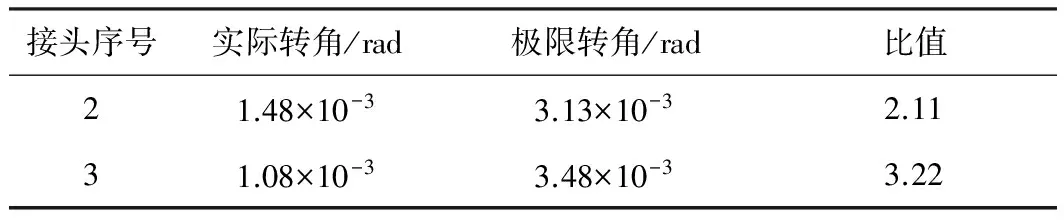
接头序号实际转角/rad极限转角/rad比值21.48×10-33.13×10-32.1131.08×10-33.48×10-33.22
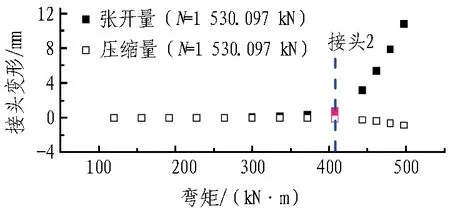
(a) 接头2张开与压缩量

(b) 接头3张开与压缩量
4 结论与建议
基于足尺力学实验的结果,采用三维有限元精细化模型对带有接头盒的一类600 mm厚大断面矩形盾构管片进行了接头受力的数值模拟,该数值模型可以较好地吻合足尺力学试验的结果。研究了此类接头形式在正负弯矩工况下抗弯刚度的组成与模式,同时依据3项分析指标定性地评价了各个接头在正常使用阶段的工作性态,此外依据接头转角与张开量的数值大小对接头力学性态进行了定量评价,结果可作为此类管片接头设计的参考。
依据试验和有限元分析结果,接头的受力过程大致经历了弹性、塑性软化与破坏3个阶段,但两者略有不同,正弯矩工况下螺栓充分发挥了抗拉性能,使得塑性软化阶段比较明显,接头具有一定的安全储备;负弯矩工况下螺栓迅速屈服,导致接头塑性软化阶段不明显,结构的破坏呈现明显脆性。主要的结论与建议如下。
1)对于正弯矩工况下的接头,各部件均处于弹性工况,接头设计与位置选择合理,在正常使用条件下具有一定的安全储备。弯矩-转角全过程曲线呈现三折线模式,各接头受力均处于第2阶段,转动刚度约为100 MN·m/rad。
2)对于负弯矩工况下,弯矩-转角全过程曲线呈现双折线模式,各接头受力均处于第1阶段,转动刚度约为276 MN·m/rad。接头受力接近2阶段的临界位置,所受弯矩值偏大。为保证设计的安全性,建议略微调整负弯矩接头的位置,以保证接头的正常使用。
3)在正弯矩工况下,铸铁盒连接件在试验中出现了侧壁撕裂现象,同时连接的锚筋也被拔出。因此,在此类接头极限承载力设计的过程中,除了考虑受压区混凝土压碎与螺栓受拉屈服,还应重点考虑铸铁盒尺寸以及锚固方式。对于接头盒局部构造,还需进一步设计和研究。
[1] 鲁亮, 孙越峰, 柳献, 等. 地铁盾构隧道足尺整环结构极限承载能力试验研究[J]. 结构工程师, 2012, 28(6): 134.
LU Liang, SUN Yuefeng, LIU Xian, et al. Full-ring experi-mental study of the ultimate bearing capacity of the lining structure of the metro shield tunnel[J]. Structural Engineers, 2012, 28(6): 134.
[2] 柳献, 唐敏, 鲁亮, 等. 内张钢圈加固盾构隧道结构承载能力的试验研究: 整环加固法[J]. 岩石力学与工程学报, 2013(11): 2300.
LIU Xian, TANG Min, LU Liang, et al. Experimental study of ultimate bearing capacity of shield tunnel reinforced by full-ring steel plate[J]. Chinese Journal of Rock Mechanics and Engineering, 2013(11): 2300.
[3] 封坤, 何川, 苏宗贤. 南京长江隧道管片衬砌结构原型加载试验[J].中国公路学报, 2013(1): 135.
FENG Kun, HE Chuan, SU Zongxian. Prototype loading test on segmental lining structure of Nanjing Yangtze River Tunnel[J]. China Journal of Highway and Transport, 2013(1): 135.
[4] 毕湘利, 柳献, 王秀志, 等. 通缝拼装盾构隧道结构极限承载力的足尺试验研究[J].土木工程学报, 2014(10): 117.
BI Xiangli, LIU Xian, WANG Xiuzhi, et al. Experimental investigation on the ultimate bearing capacity of continuous-jointed segmental tunnel linings[J].China Civil Engineering Journal, 2014(10): 117.
[5] 闫治国, 彭益成, 丁文其,等. 青草沙水源地原水工程输水隧道单层衬砌管片接头荷载试验研究[J]. 岩土工程学报, 2011, 33(9): 1385.
YAN Zhiguo, PENG Yicheng, DING Wenqi, et al. Load tests on segment joints of single lining structure of shield tunnel in Qingcaosha water conveyance project[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1385.
[6] 徐国文, 王士民, 汪冬兵. 基于接头抗弯刚度非线性的壳-弹簧-接触-地层模型的建立[J]. 工程力学, 2016, 33(12): 158.
XU Guowen, WANG Shimin, WANG Dongbing. Shell-spring-contact-ground model based on segment joint stiffness nonlinearity[J]. Engineering Mechanics, 2016, 33(12): 158.
[7] 程小虎. 梁单元模拟管片接头的盾构衬砌计算模型[J]. 地下空间与工程学报, 2010, 6(5): 946.
CHENG Xiaohu. Calculation model of shield tunnel segment with joints simulated by beam element[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(5): 946.
[8] 曾东洋, 何川. 地铁盾构隧道管片接头抗弯刚度的数值计算[J]. 西南交通大学学报, 2004, 39(6): 744.
ZENG Dongyang, HE Chuan. Numerical simulation of segment joint bending stiffness of metro shield tunnel[J]. Journal of Southwest Jiaotong University, 2004, 39(6): 744.
[9] 张建刚, 何川. 管片接头力学解析法: 改进条带算法[J]. 铁道学报, 2013, 35(3): 102.
ZHANG Jiangang, HE Chuan. Mechanical calculation method of segmental joints: Improved strip method [J]. Journal of the China Railway Society, 2013, 35(3): 102.
[10] 孙文昊, 焦齐柱, 薛光桥,等. 盾构隧道管片无衬垫接头抗弯刚度研究[J]. 地下空间与工程学报, 2008(5): 973.
SUN Wenhao, JIAO Qizhu, XUE Guangqiao, et al. Study of bending stiffness of nonliner segment joint in shield tunnel[J]. Chinese Journal of Underground Space and Engineering, 2008(5): 973.
[11] 朱合华, 陶履彬. 盾构隧道衬砌结构受力分析的梁-弹簧系统模型[J]. 岩土力学, 1998(2): 26.
ZHU Hehua, TAO Lübin. Beam-spring system model for stress analysis of shield tunnel lining structure[J]. Rock and Soil Mechanics, 1998(2): 26.
[12] 朱伟, 黄正荣, 梁精华. 盾构衬砌管片的壳-弹簧设计模型研究[J]. 岩土工程学报, 2006, 28(8): 940.
ZHU Wei, HUANG Zhengrong, LIANG Jinghua. Studies on shell-spring design model for segment of shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(8): 940.
[13] 张鹏. 盾构隧道管片接头力学性能三维数值计算研究[J]. 铁道勘测与设计, 2012(2): 54.
ZHANG Peng. Three dimensional numerical study of mecha-nical properties of shield tunnel segment joint[J]. Railway Survey and Design, 2012(2): 54.
[14] 张厚美, 张正林, 王建华. 盾构隧道装配式管片接头三维有限元分析[J]. 上海交通大学学报, 2003, 37(4): 566.
ZHANG Houmei, ZHANG Zhenglin, WANG Jianhua. 3-D FEM analysis on prefabricated segment joints of shield tunnel[J]. Journal of Shanghai Jiaotong University, 2003, 37(4): 566.
[15] 王东方, 张维熙, 董子博, 等. 类矩形盾构隧道衬砌结构受力的现场试验研究[J]. 现代隧道技术, 2016, 53(6): 174.
WANG Dongfang, ZHANG Weixi, DONG Zibo, et al. Exper-imental field study on the structural behaviors of the linings of quasi-rectangular shield tunnels[J]. Modern Tunnelling Technology, 2016, 53(6): 174.
[16] 叶宇航, 黄德中, 李刚,等. 类矩形盾构隧道衬砌结构极限承载力足尺试验研究[J]. 现代隧道技术, 2016(增刊1): 118.
YE Yuhang, HUANG Dezhong, LI Gang, et al. The full-scale test of the rectangular shield tunnel lining structure ultimate bearing capacity[J]. Modern Tunnelling Technology, 2016(S1): 118.
[17] 雷拓, 钱江, 刘成清. 混凝土损伤塑性模型应用研究[J]. 结构工程师, 2008, 24(2): 22.
LEI Tuo, QIAN Jiang, LIU Chengqing. Application of damaged plasticity model for concrete[J]. Structual Engineers, 2008, 24(2): 22.
[18] 秦浩, 赵宪忠. ABAQUS混凝土损伤因子取值方法研究[J]. 结构工程师, 2013, 29(6): 27.
QIN Hao, ZHAO Xianzhong. Study of the ABAQUS damage parameter in the concrete damage plasticity model[J]. Structual Engineers, 2013, 29(6): 27.
[19] 庄晓莹, 张雪健, 朱合华. 盾构管片接头破坏的弹塑性-损伤三维有限元模型研究[J]. 岩土工程学报, 2015, 37(10): 1826.
ZHUANG Xiaoying, ZHANG Xuejian, ZHU Hehua. 3-D finite element model for destruction process of segment joints of shield tunnel using elastoplastic and damage constitutive methods[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(10): 1826.
[20] 朱瑶宏, 柳献, 张晨光, 等. 地铁盾构隧道纵缝接头螺栓形式对比试验研究[J]. 铁道科学与工程学报, 2015(6): 1427.
ZHU Yaohong,LIU Xian,ZHANG Chenguang, et al. Contrast test research on longitudinal jo-int with different forms of bolts in metro shield tunnel[J]. Journal of Railway Science and Engineering, 2015(6): 1427.
[21] 严佳梁. 盾构隧道管片接头性态研究[D].上海: 同济大学,2006.
YAN Jialiang. Research on joint of shield tunnel segment[D]. Shanghai: Tongji University, 2006.
FiniteElementAnalysisofMechanicalBehaviorforNewTypeofSegmentJointsofRectangularShieldTunnel
WEI Yuliang1, 2, DING Wenqi1, 2, JIN Yuelang1, 2, GONG Chenjie1, 2, JIANG Hong3
(1.DepartmentofGeotechnicalEngineering,CollegeofCivilEngineering,TongjiUniversity,Shanghai200092,China; 2.KeyLaboratoryofGeotechnicalandUndergroundEngineeringofMinistryofEducation,TongjiUniversity,Shanghai200092,China; 3.ShanghaiMunicipalEngineeringDesignInstitute(Group)Co.,Ltd.,Shanghai200125,China)
A fined 3D calculation model of longitudinal joints of large cross-section rectangular shield tunnel with embedded parts is established by finite element software ABAQUS based on full-scale mechanical testing results, so as to analyze and estimate the rationality of the segment joint structure and stressing. The working states of every joint under normal operating conditions are estimated qualitatively and quantitatively; and then the stressing characteristics of joint under positive and negative bending moment are studied. The results show that: 1) The bending moment-rotation angle curve of the segment presents a three-fold line mode under positive bending moment. The joints are in the second stage under normal operating condition, where the rotational stiffness is about 100 MN·m/rad; the components are all in elastic condition and the design and location of the joints are rational. 2) The bending moment-rotation angle curve of the segment presents a double-fold line mode under negative bending moment. The joints are all in the first stage under normal operating condition, where the rotational stiffness is about 276 MN·m/rad. However, the negative bending moment is quite large and the safety stiffness is low, which should be paid more attentions to in design.
segment joint of rectangular shield tunnel; mechanical behavior; fined 3D finite element model
2017-06-10;
2017-07-22
国家自然科学基金资助项目(51378388); 上海市科委项目(15XD1522500, 16DZ1201701, 17DZ1203402)
魏于量(1994—),男,江苏扬中人,同济大学土木工程专业在读硕士,主要研究方向为软土盾构隧道接头力学。E-mail: 1025174830@qq.com。
10.3973/j.issn.1672-741X.2017.10.015
U 45
A
1672-741X(2017)10-1309-08
