基于流-固耦合的盾构隧道开挖面稳定性研究

康志军， 谭 勇， 李金龙

(1. 保利(成都)实业有限公司， 四川 成都 610000; 2. 同济大学土木工程学院地下建筑与工程系， 上海 200092)

基于流-固耦合的盾构隧道开挖面稳定性研究

康志军1， 2， 谭 勇2， *， 李金龙2

(1. 保利(成都)实业有限公司， 四川 成都 610000; 2. 同济大学土木工程学院地下建筑与工程系， 上海 200092)

利用FLAC3D建立三维数值模型，对考虑完全流-固耦合效应的盾构隧道开挖面失稳过程进行模拟和验证，并进一步分析水位高度、渗流时间对开挖面变形、地表沉降和孔隙水压力的影响。研究表明： 开挖面变形随支护压力比的减小经历3个阶段的变化,且与土体塑性区的发展密切相关； 相比于无水状态，考虑流-固耦合效应的开挖面稳定性显著降低，随水位的升高、渗流时间的增大，开挖面发生失稳破坏的支护压力比明显增大； 支护压力比(表征支护压力)的减小将导致开挖面前方一定范围的孔隙水压力减小，靠近开挖面的孔隙水压力受扰动程度加剧，形成“漏斗状”的影响区； 开挖面失稳导致土体位移场延伸至地表，引起地表产生明显的沉降变形，在不同的变形阶段开挖面中心点位移与最大地表沉降分别呈抛物线相关和线性相关。

盾构隧道； 开挖面稳定； 流-固耦合； 支护压力； 地层变形； 孔隙水压力

0 引言

随着我国地下工程的大规模开发利用，盾构法被越来越多地应用到工程实践中，但随之而来的是一系列的工程事故，其中最为突出的便是由于开挖面支护压力比不足导致的开挖面失稳及土层变形过大[1]。特别是当盾构在水下施工时，由于浅覆土和高水压的不利因素，地下水渗流导致的渗透力将显著影响开挖面稳定性，稍有不慎便会引发开挖面坍塌和水体倒灌等事故[2]。

近年来，诸多学者利用解析方法、数值仿真模拟与离心试验等手段针对渗流条件下的开挖面稳定性进行了一系列的研究。Anagnostou等[3]采用楔形体模型研究了渗流对开挖面稳定性的影响。Lee等[4]基于极限平衡、极限分析上限法和有限元法计算了渗流条件下维持开挖面稳定的极限支护压力。Buhan等[5]结合地下水渗流产生的渗透力作用对盾构隧道开挖面进行了数值仿真分析，发现其在开挖面稳定性中起关键作用。De Broere等[6]认为泥水渗入地层是非固定的渗流问题，其产生的渗透力作用将影响开挖面稳定安全系数。Schweiger等[7]通过分析考虑渗流力影响的开挖面支护压力，发现平衡渗流力是开挖面支护压力的重要组成部分。高健等[8]采用有限差分数值计算程序得出随着地下水位的升高，渗透力在总支护力中的比值呈升高趋势。黄正荣等[9]通过数值模拟分析了不同地下水位下支护压力与开挖面变形及稳定系数的关系，发现地下水会给隧道开挖面稳定带来较大影响。

目前研究地下水渗流对开挖面稳定性的影响时，往往选择先在渗流场中计算至稳态渗流状态、计算得到此时的渗透力，然后将其作为应力边界条件施加于力学平衡计算中，并未考虑应力场和渗流场的耦合效应，并且鲜有关于水位线位于地表以上的高水压条件的研究。因此，本文通过数值模拟方法且考虑流-固耦合效应，针对高水压条件下盾构隧道的开挖面稳定性开展研究。

1 模拟开挖面失稳的数值模型及验证

1.1计算方法提出

根据文献[10-11]的数值模拟方法，假定盾构处于停机状态，通过逐级减小开挖面支护压力，并设置一定的渗流时间以进行完全流-固耦合计算，作出开挖面中心点水平位移与开挖面支护压力比的关系曲线，随着支护压力比的减小开挖面中心点的水平位移逐渐增大，当支护压力比变化很小而开挖面中心点的水平位移急剧增大时，认为此时开挖面发生失稳破坏。

模拟开挖面失稳的数值计算流程如图1所示。

由于隧道开挖面支护力为梯形分布形式，本文取隧道开挖面中心点的支护力来代表开挖面的支护力，对于开挖面支护力大小的表示，引入支护压力比的概念：

σs=λ·σ0。

(1)

式中：σs为开挖面中心点的支护压力值；λ为支护压力比；σ0为原始地层在开挖面中心点的静止水平土压力值。

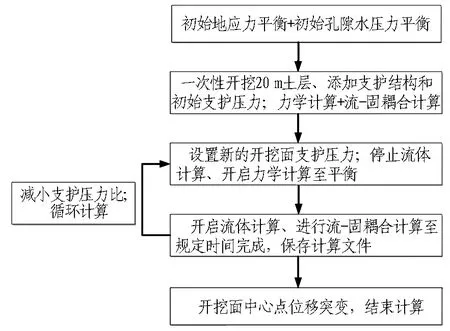
图1 循环计算示意图

1.2计算方法验证

为了验证上文提出的模拟开挖面失稳的数值计算方法的合理性，参考吕玺琳等[12]的离心试验模型建立数值模型进行计算，对比结果如图2所示。由图2可以看到： 在干砂和饱和砂地层中，数值模拟和离心试验得到的开挖面中心点位移曲线的吻合程度较好、开挖面发生失稳破坏的极限支护压力相近。

图2 数值模拟和离心试验得到的开挖面中心点位移曲线Fig. 2 Developing curves of horizontal displacement at center of tunneling face by simulations and centrifuge tests

2 数值模型建立

2.1模型几何及边界条件

本文设定隧道直径D=10 m、覆土厚度C=10 m、水位线位于地表处。为消除数值模型边界效应对计算结果的影响，设置模型竖向长度Lz=50 m、水平向长度Lx=30 m、沿隧道纵向长度Ly=50 m。地表设定为自由边界、模型四周设置法向位移约束、模型底部设置为固定边界；计算过程中水位保持不变，在实际工程中，水下盾构停机过程中通常采取良好的渗透控制措施，故设定隧道开挖面和衬砌结构为不透水边界；模型中第2节的数值模型未考虑基础土体损失和盾尾注浆压力的影响。模型网格划分如图3所示。

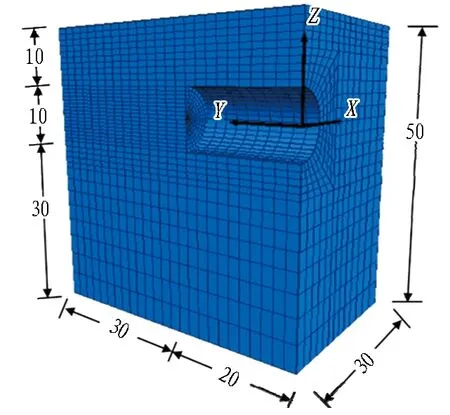
图3 模型网格划分图(单位： m)

2.2数值模型参数取值

本文设定土体是各向同性均匀分布的理想弹塑性

体，服从摩尔-库仑屈服准则；盾构管片材料为C50钢筋混凝土材料，厚度为0.35 m，采用SHELL单元模拟，土体参数参考周小文等[13-14]离心试验模型的土样，土体及管片材料力学参数如表1所示。在流-固耦合计算中，土体参数指标均采用有效应力指标，初始静止水平土压力采用水土分算法，计算公式如下：

σ0=γw·h+K0·γ′·h；

(2)

γ′=γs-γw。

(3)

式中：γw为水的重度；h为土层高度；γ′为土体浮重度；γs为土体饱和重度。

模拟中流体设置为各向同性模型。通过反分析手段，设定不同的渗流时间，选取与试验数据吻合程度较高的工况，最终设置流-固耦合计算中渗流时间T=2 h，流体计算参数如表2所示。

表1 土体及管片物理力学参数

表2 渗流计算参数

2.3计算结果分析

2.3.1 开挖面中心点位移

图4示出不同支护压力比下开挖面中心点位移曲线，图5示出土体塑性区发展。开挖面中心点位移曲线经历3个阶段的发展： 当支护压力比在0.6～1.0范围时，中心点位移缓慢地增长，此时开挖面前方土体塑性区影响范围有限，可认为开挖面处于弹性变形阶段；当支护压力比在0.6～0.4范围内，位移曲线的斜率有一定程度的增大、塑性区向开挖面前方发展，可认为开挖面处于弹塑性变形阶段；当支护压力比减小至0.3时，曲线发生断崖式的下跌(中心点位移由9 cm急剧地增大至91 cm)，开挖面发生整体失稳破坏，此时塑性区由开挖面贯通至地表，可认为开挖面进入完全塑性变形阶段。图4中还列出了不考虑流-固耦合作用的模拟数据，此时开挖面发生失稳破坏的支护压力比明显偏小： 当支护压力比从0.2减小至0.1时，中心点位移发生急剧地突变，这与朱伟等[15]的研究结论相似。

2.3.2 开挖面失稳破坏模式

图6示出支护压力比为0.3的土体位移云图。开挖面的失稳破坏模式与吕玺琳等[12]离心试验结果相似：开挖面前方呈楔形体形态，其上为扩展的烟囱状形态，形成由开挖面延伸至地表的整体滑动区。

2.3.3 土体孔隙水压力

图7示出开挖面中心点前方土体孔隙水压力变化曲线，正值为增大、负值为减小。在流-固耦合作用下，开挖面前方土体孔隙水压力减小，随支护压力比的减小、孔隙水压力减小程度逐渐增大；靠近开挖面的孔隙水压力受扰动程度较大、主要影响范围延伸至开挖面前方15 m左右。

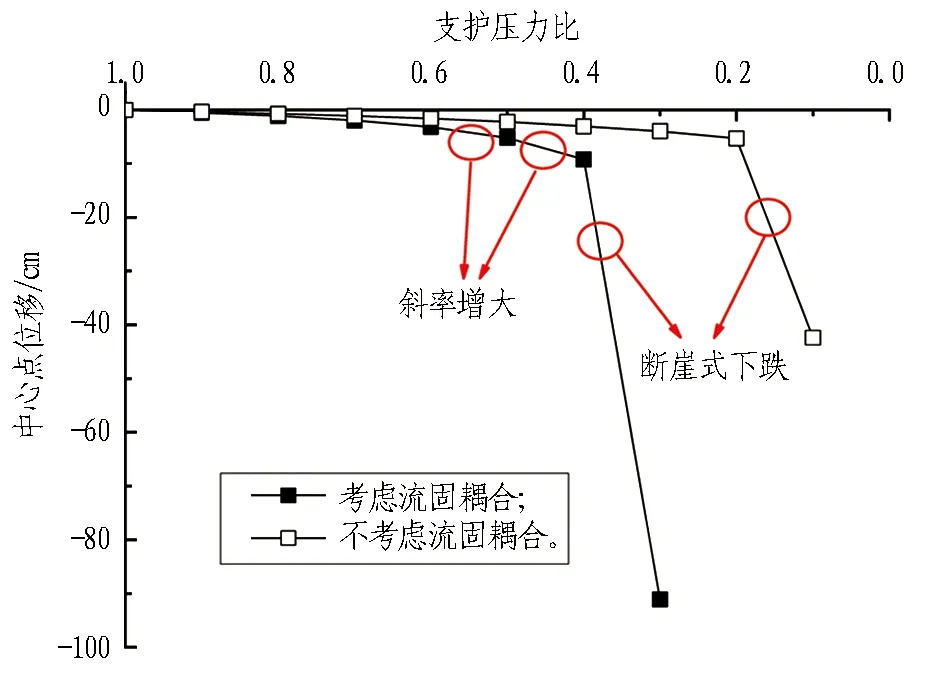
图4 不同支护压力比λ下开挖面中心点位移曲线Fig. 4 Developing curves of horizontal displacement at center of tunneling face under different values of λ

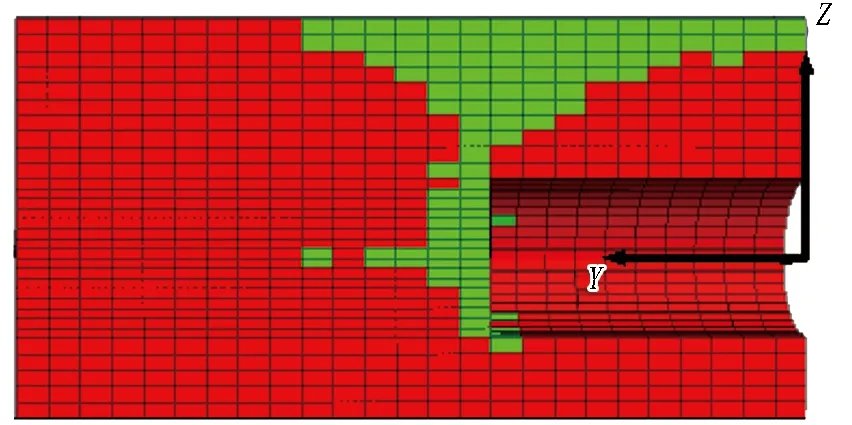
(a) λ=0.6

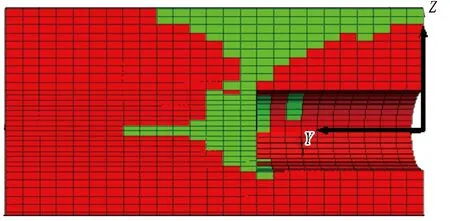
(b) λ=0.5

(c) λ=0.4

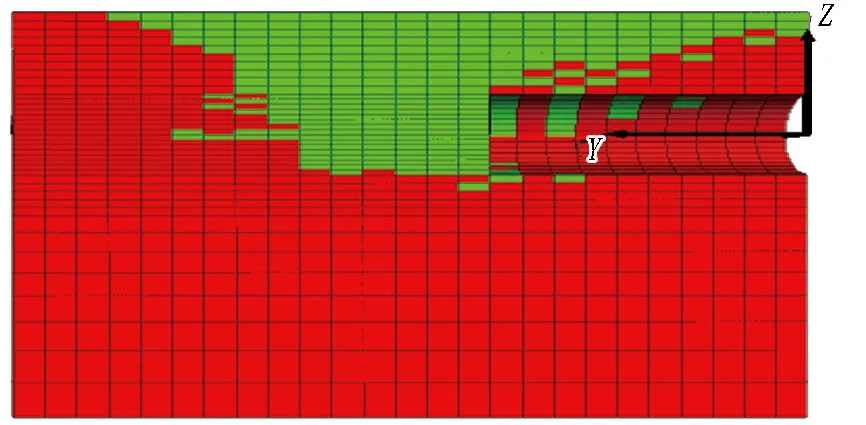
(d) λ=0.3

图6 λ=0.3的土体位移云图(单位： cm)

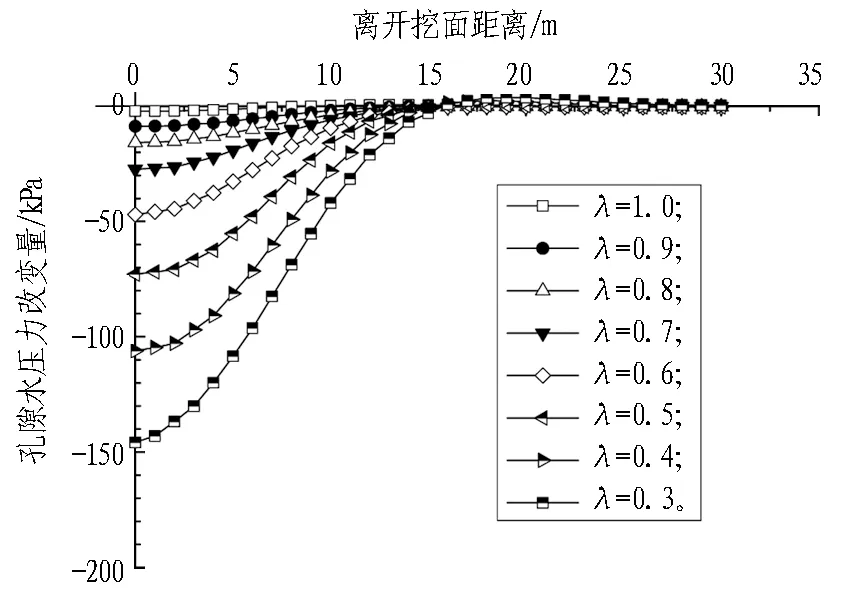
图7 开挖面前方孔隙水压力变化曲线Fig. 7 Variation curves of pore pressure in front of tunneling face

图8为土体孔隙水压力云图。当支护压力比为1时，由于开挖面产生微小的变形，土体孔隙水压力无明显变化；当支护压力比为0.3时，开挖面产生较大变形，在流-固耦合作用下，开挖面前方土体孔隙水压力明显减小，并逐渐影响上部浅层土体，形成“漏斗状”的孔隙水压力影响区。

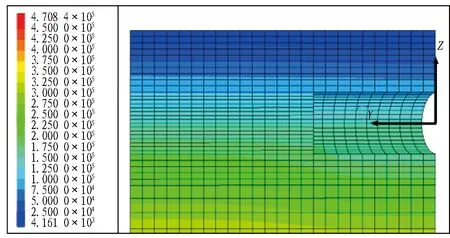
(a) λ=1.0

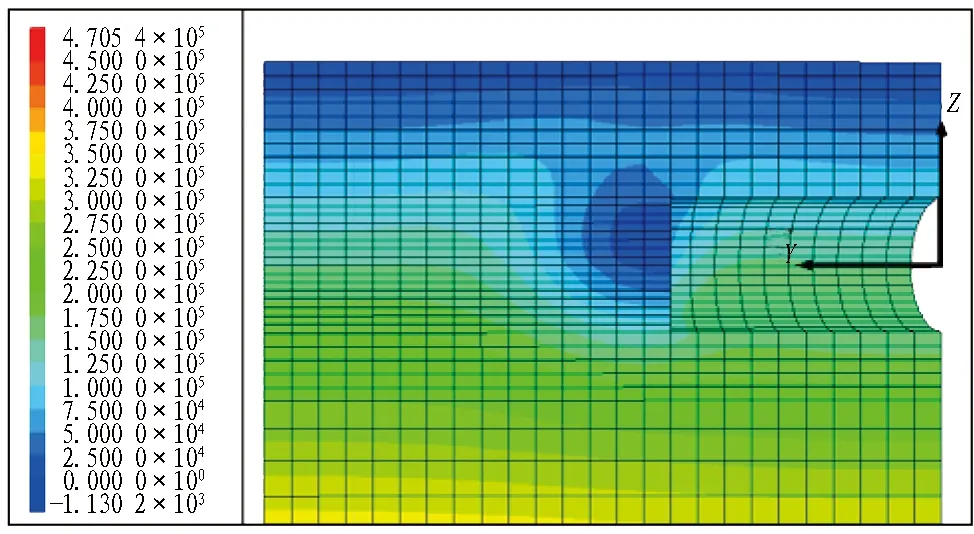
(b) λ=0.3

2.3.4 土体应力路径曲线

图9示出开挖面中心点前方土体应力路径变化曲线。随支护压力比的减小，开挖面中心点前方土体应力状态经历2个阶段的变化： 应力路径曲线先上升至拐点后经历下降，这表明土体应力状态从弹性状态逐渐发展至塑性状态；随离开挖面距离的增大，应力路径曲线到达拐点的支护压力比减小，且土体应力水平大于靠近开挖面位置处，这表明靠近开挖面的土体受扰动程度较大，这与图5中土体塑性区的发展趋势相同。

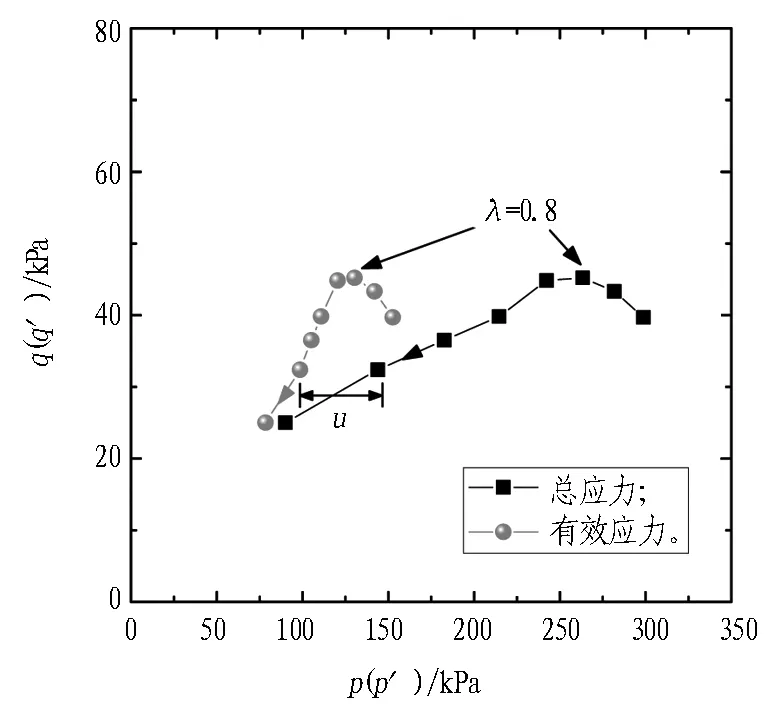
(a) 开挖面前方2 m

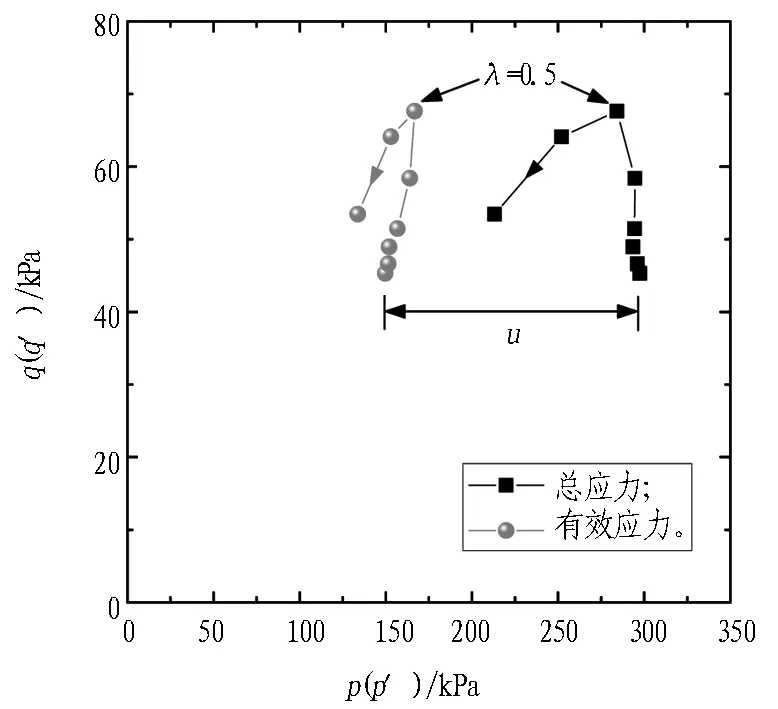
(b) 开挖面前方8 m

3 参数分析

在第2节中详细地分析了基于流-固耦合效应的条件下支护压力对开挖面稳定性各方面的影响，本节将开展变参数分析。

3.1水位条件对开挖面稳定性的影响

以第2节的数值模型为基础，设置水位线位于地表以上不同高度(H=0、20、40、60、80、100 m)为单一变量的工况，研究水位条件对开挖面稳定性的影响。

3.1.1 开挖面中心点位移

图10示出不同水位条件的开挖面中心点位移曲线。随水位的升高，开挖面发生失稳破坏的支护压力比增大，即开挖面稳定性显著降低；在支护压力比相同的条件下，水位越高，位移值越大，当水位为60、80、100 m时，支护压力比减小至0.7时，曲线斜率有明显的增大，且水位越高斜率增大的趋势越明显。

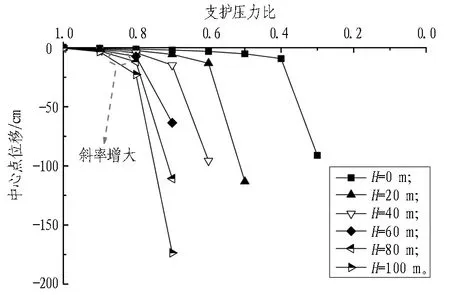
图10 不同水位条件的开挖面中心点位移曲线Fig. 10 Developing curves of horizontal displacement at center of tunneling face under different water levels

3.1.2 地表沉降

图11示出支护压力比为0.7的纵向地表沉降曲线。同开挖面中心点位移曲线发展趋势类似： 水位高于 60 m工况的沉降曲线发生明显的突变，最大沉降值远大于其余低水位工况，沉降曲线呈非对称的凹槽型分布，最大沉降发生在开挖面前方5 m附近，主要沉降影响区为开挖面后方5 m至前方20 m范围。

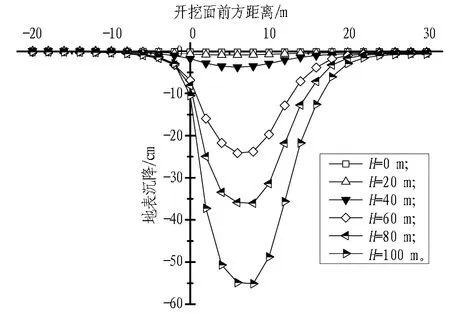
图11 λ= 0.7的纵向地表沉降曲线

图12示出支护压力比为0.7的开挖面前方5 m横向地表沉降曲线。横向地表沉降曲线呈凹槽型分布，最大沉降发生在隧道轴线上方，主要沉降影响区为离轴线15 m范围以内；同纵向地表沉降规律类似，水位高于60 m工况的沉降曲线发生明显的突变，最大沉降值远大于其余低水位工况。

3.1.3 孔隙水压力变化

图13示出支护压力比为0.7时开挖面中心点前方土体孔隙水压力变化曲线。在流-固耦合作用下，开挖面前方土体孔隙水压力减小，水位越高、相同位置处的孔隙水压力减小量越大；随离开挖面距离的增大，孔隙水压力减小量逐渐降低，随水位的升高，主要影响范围逐渐扩大。

图12 λ= 0.7的横向地表沉降曲线

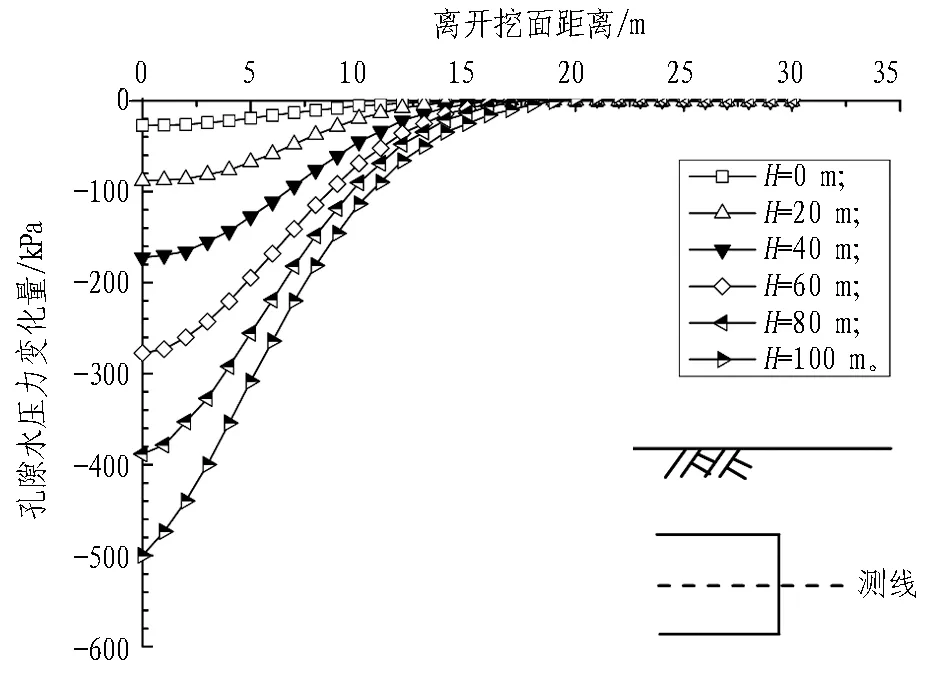
图13 λ= 0.7的开挖面前方孔隙水压力变化曲线Fig. 13 Variation curves of pore pressure in front of tunneling face when λ= 0.7

图14示出开挖面前方1 m位置土体孔隙水压力变化曲线。随支护压力比的减小，孔隙水压力减小量增大，水位越高，曲线斜率越大，即孔隙水压力减小量越大。

图14 不同水位条件H的开挖面前方1 m孔隙水压力变化曲线Fig.14 Variation curves of pore pressure 1 m in the front of tunneling face under different water levels

3.2渗流时间对开挖面稳定性的影响

在流-固耦合计算中，渗流时间是最重要的参数之一，本文数值模型中的渗流时间对应着盾构停机时长。本节取水位线位于地表以上20 m、设定渗流时间T=1、2、3、6 h为单一变量的工况，以研究渗流时间对开挖面稳定性的影响。

3.2.1 开挖面中心点位移

图15示出开挖面中心点水平位移随支护压力比的变化曲线。当支护压力为1.0～0.7时，4种工况的位移曲线几乎重合，即支护压力比较大时，渗流时间对开挖面变形影响较小；当支护压力比减小至0.6时，渗流6 h工况的位移值急剧增大至130 cm,此时开挖面发生失稳破坏，而渗流3 h工况的位移值也有明显的增大；当支护压力比减小至0.5时，3种工况的位移曲线有明显的突变。总体来说，渗流时间越长,位移值越大，开挖面发生失稳破坏的支护压力比越大。

图15 不同渗流时间T的开挖面中心点位移曲线Fig. 15 Developing curves of horizontal displacement at center of tunneling face under different seepage times

图16为支护压力比为0.6的土体位移等值图。由图16可以看到： 随渗流时间的增大，土体位移量值逐渐增大，且主要位移影响区逐渐向地表扩散；渗流时间T=1 h工况的最大位移值为11 cm，发生在开挖面上部区域，引起地表产生2 cm左右的变形； 渗流时间T=6 h工况的最大位移值急剧增大至180 cm，发生在开挖面下部区域，引起地表产生超过50 cm的变形。

3.2.2 孔隙水压力变化

图17示出支护压力比为0.6的开挖面前方中心点前方孔隙水压力变化曲线。在流-固耦合作用下，开挖面前方的土体孔隙水压力明显降低，主要影响区为开挖面前方15～20 m，渗流时间越长主要影响区范围越大；在靠近开挖面的范围内(0～7.5 m)，渗流时间越长，孔隙水压力减小量越小，而在此范围之外情况则相反。

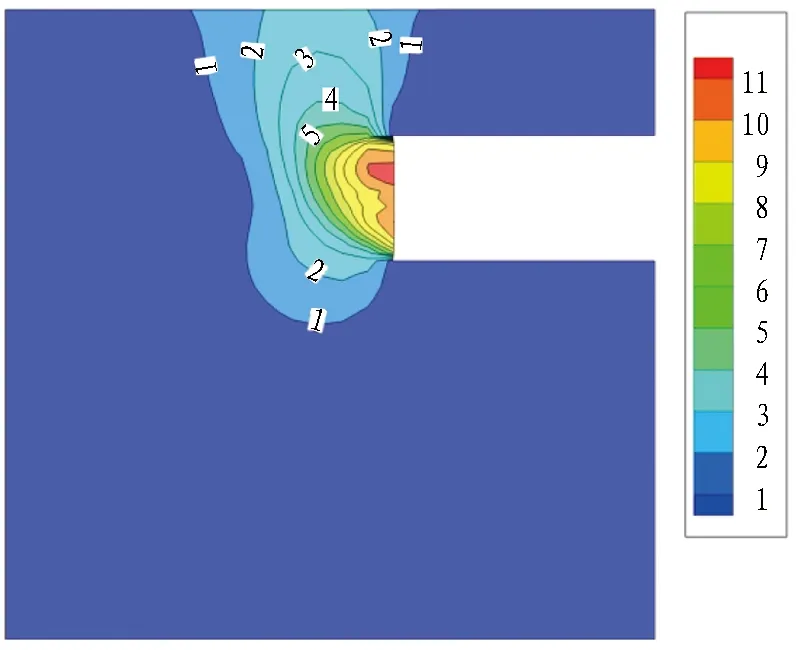
(a) T=1 h

(b) T= 6 h

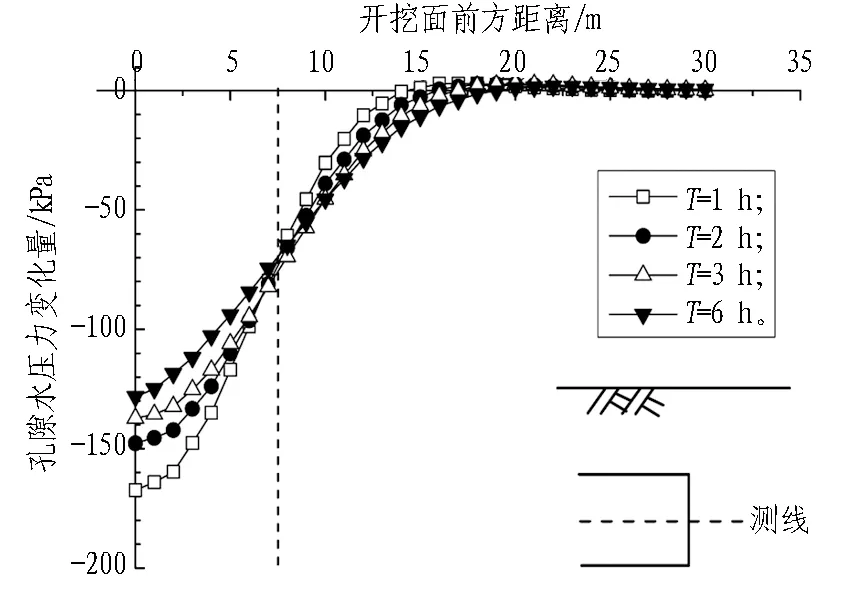
图17 λ= 0.6的开挖面中心点前方孔隙水压力变化曲线Fig. 17 Variation curves of pore pressure in front of tunneling face when λ= 0.6

图18示出开挖面中心点前方1 m孔隙水压力变化曲线。随支护压力比的减小，孔隙水压力减小程度增大，渗流时间越长，孔隙水压力减小量降低，即孔隙水压力趋于初始平衡状态。

图19为支护压力比为0.6的土体孔隙水压力云图。由图19可以看到： 渗流1 h工况的开挖面前方土体孔隙水压力受扰动程度较大，但渗流6 h工况对开挖面上方的浅层土体孔隙水压力影响程度更明显，形成“漏斗状”的孔隙水压力影响区。

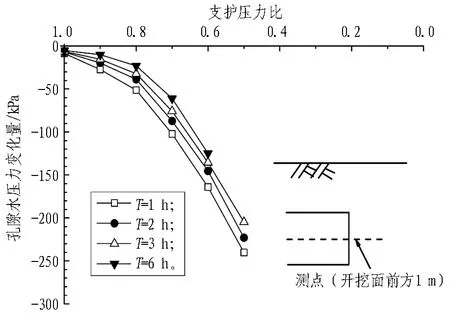
图18 不同渗流时间T的开挖面前方1 m孔隙水压力变化曲线Fig. 18 Variation curves of pore pressure 1 m in the front of tunneling face under different seepage times

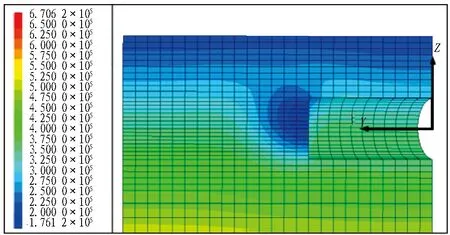
(a) T=1 h

(b) T= 6 h

3.3开挖面中心点位移与最大地表沉降关系

在实际工程中，盾构隧道开挖面变形的监测难度较大，通常采取监测地表沉降的手段来评估盾构隧道掘进对周围环境的影响。

基于前文的一系列数值模型，得到不同支护压力比条件下开挖面中心点位移值与最大纵向地表沉降的关系，如图20所示。由图20可以看到： 开挖面中心点水平位移值大于最大地表沉降值，在不同的变形阶段，二者呈不同的相关性，当开挖面位移小于25 cm时，二者呈明显的抛物线相关，这与陈仁朋等[16]在干砂地层中的离心试验结论类似；当开挖面位移大于25 cm时，数据点呈现一定的离散性，但二者呈明显的线性相关；在隧道埋深比一定的条件下，水位高度和渗流时间并未明显影响二者的相关性。

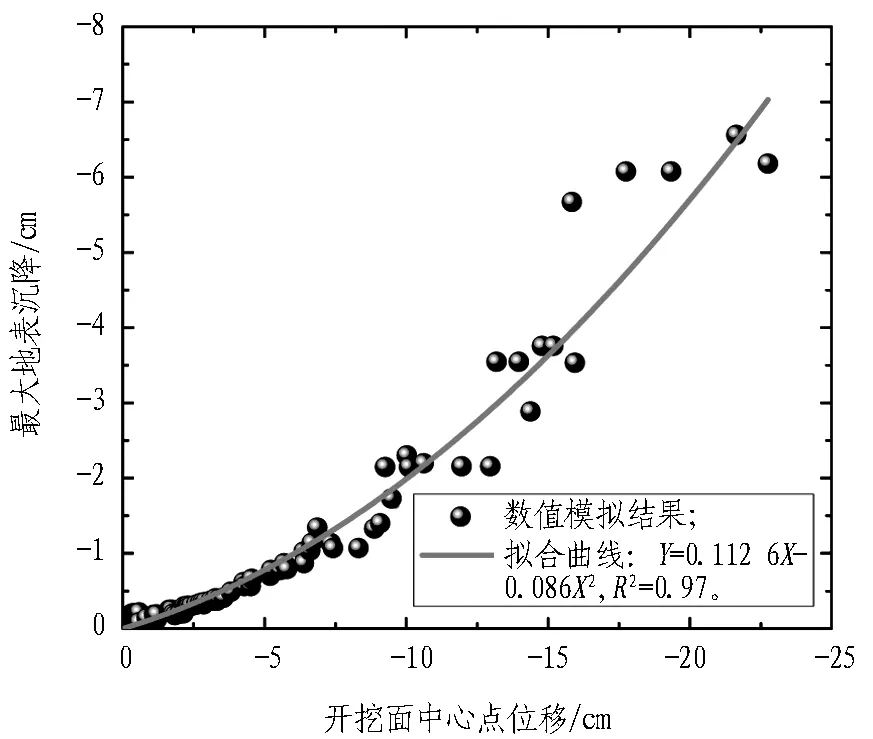
(a) 位移值较小

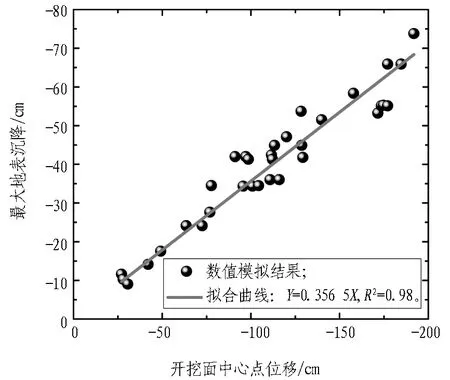
(b) 位移值较大

4 结论与讨论

本文建立了考虑流-固耦合效应的数值模型，针对盾构处于停机状态的开挖面稳定性问题开展了研究，并重点讨论了水位条件和渗流时间的影响，得出以下结论：

1)开挖面变形随支护压力比的减小经历3个发展阶段： 缓慢增长、变形速率增大和整体失稳破坏，与土体塑性区的发展趋势相符合，且靠近开挖面的土体受扰动程度明显偏大；

2)考虑流-固耦合效应的开挖面发生失稳的支护压力比大于不考虑流-固耦合效应，随水位的升高、渗流时间的增大，开挖面稳定性降低，发生失稳破坏的支护压力比明显增大；

3)在流-固耦合作用下，支护压力的减小将导致开挖面前方一定范围的孔隙水压力降低，随水位的升高、渗流时间的缩短，孔隙水压力减小程度增大；

4)随水位的升高、渗流时间的增大，开挖面变形加剧，并引起土体位移场延伸至地表，形成明显的沉降变形区；

5)开挖面中心点水平位移与最大地表沉降在不同变形阶段呈不同的相关性，位移较小时，二者呈抛物线相关，位移较大时，二者呈线性相关。

需要特别指出，由于数值模拟方法本身的局限性，在数值模拟中，只有通过设定盾构开挖面处于某一特定位置不变(即本文所言停机状态)，通过减小支护压力才能达到隧道失稳的目的。因此，大部分的数值模拟研究都是设定盾构处于类似的停机状态来模拟研究隧道开挖面稳定性问题。虽然数值模拟假定与实际工况有较大出入，但只要模型合理，相数值模拟分析还是能较为真实模拟实际情况。

[1] 高健. 考虑渗流的盾构隧道掘进面失稳分析[D]. 天津： 天津大学, 2010.

GAO Jian. Analysis of face instability of shield tunnels with consideration of groundwater seepage[D]. Tianjin： Tianjin University, 2010.

[2] 陈孟乔. 高水压砂土地层中泥水盾构隧道开挖面失稳机理与风险评估研究[D]. 北京： 北京交通大学, 2014.

CHEN Mengqiao. Study of instability mechanism and risk assessment of slurry shield tunneling face in sands under high hydraulic pressure[D]. Beijing： Beijing Jiaotong University, 2014.

[3] ANAGNOSTOU G, KOVARIK. Face stability conditions with earth-pressure-balanced shields[J]. Tunnelling and Underground Space Technology, 1996, 11(2): 165.

[4] LEE I M, NAM S W. The study of seepage forces acting on the tunnel lining and tunnel face in shallow tunnels[J]. Tunnelling and Underground Space Technology, 2001, 16(1): 31.

[5] DE BUHAN P, CUVILLIER A, DORMIEUX L, et al. Face stability of shallow circular tunnels driven under the water table: A numerical analysis[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1999, 23(1): 79.

[6] BROERE W, VAN TOl A. Influence of infiltration and groundwater flow on tunnel face stability[C]// Geotechnical Aspects of Underground Construction in Soft Ground. Tokyo: [s.n.], 2000: 339.

[7]SCHWEIGER H F, POTTLER R K, Steiner H. Effect of seepage forces on the shotcrete lining of a large undersea cavern[C]// International Conference on Computer Methods and Advances in Geomechanics. Rotterdam: Balkema, 1991: 1503.

[8] 高健, 张义同, 乔金丽. 渗透力对隧道开挖面稳定性影响分析[J]. 岩土工程学报, 2009, 31(10): 1547.

GAO Jian, ZHANG Yitong, QIAO Jinli. Face stability analysis of tunnels with consideration of seepage force[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10): 1547.

[9] 黄正荣, 朱伟, 梁精华, 等. 浅埋砂土中盾构法隧道开挖面极限支护压力及稳定研究[J].岩土工程学报, 2006, 28(11): 2005.

HUANG Zhengrong, ZHU Wei, LIANG Jinghua, et al. Study of limit supporting pressure and stabilization of excavation face for shallow shield tunnels in sand[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11): 2005.

[10] 朱季. 粉砂土地基盾构施工开挖面稳定性及环境影响研究[D]. 杭州： 浙江大学, 2010.

ZHU Ji. Face stability and deformation of shield tunneling in sandy silt soil[D]. Hangzhou： Zhejiang University, 2010.

[11] 邓宗伟, 伍振志, 曹浩, 等. 基于流-固耦合的泥水盾构隧道施工引发地表变形[J]. 中南大学学报(自然科学版). 2013, 44(2): 785.

DENG Zongwei, WU Zhenzhi, CAO Hao, et al. Surface deformation of slurry shield tunneling using fluid-solid coupling theory[J]. Journal of Central South University (Science and Technology)， 2013, 44(2): 785.

[12] 吕玺琳, 周运才, 李冯缔. 粉砂地层盾构隧道开挖面稳定性离心试验及数值模拟[J]. 岩土力学，2016, 37(11): 3324.

LYU Xilin, ZHOU Yuncai, LI Fengdi. Centrifuge model test and numerical simulation of stability of excavation face of shield tunnel in silty sand[J]. Rock and Soil Mechanics， 2016, 37(11): 3324.

[13] 周小文, 濮家骝, 包承钢. 砂土中隧洞开挖稳定机理及松动土压力研究[J]. 长江科学院院报,1999,16(4): 9.

ZHOU Xiaowen, PU Jialiu, BAO Chenggang. Study of stability mechanism and relaxed soil pressure in sandy soil during excavation[J]. Journal of Yangtze River Scientific Research Institute, 1999, 16(4): 9.

[14] 周小文, 濮家骝. 砂土中隧洞开挖引起的地面沉降试验研究[J]. 岩土力学, 2002, 23(5): 559.

ZHOU Xiaowen, PU Jialiu. Centrifuge model test on ground settlement induced by tunneling in sandy soil[J]. Rock and Soil Mechanics, 2005, 23(5): 559.

[15] 朱伟, 秦建设, 卢廷浩. 砂土中盾构开挖面变形与破坏数值模拟研究[J]. 岩土工程学报, 2005, 27(8): 897.

ZHU Wei, QIN Jianshe,LU Tinghao. Numerical study of face movement and collapse around shield tunnels in sand[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(8): 897.

[16] 陈仁朋, 李君, 陈云敏, 等. 干砂盾构开挖面稳定性模型试验研究[J]. 岩土工程学报, 2011, 33(1): 117.

CHEN Renpeng, LI Jun, CHEN Yunmin, et al. Large-scale tests on face stability of shield tunnelling in dry cohesionless soil[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 117.

NumericalStudyofWorkingFaceStabilityofShieldTunnelBasedonFluid-SolidCouplingEffect

KANG Zhijun1, 2, TAN Yong2, *, LI Jinlong2

(1.Poly(CHENGDU)HoldingsCompanyLimited,Chengdu610000,Sichuan,China; 2.DepartmentofGeotechnicalEngineering,CollegeofCivilEngineering,TongjiUniversity,Shanghai200092,China)

A 3D numerical model is established by FLAC3D based on fluid-solid coupling effect, so as to simulate and verify the process of instability of tunneling face; moreover, the influences of water level and seepage time on tunneling face deformation, ground settlement and pore pressure are discussed. The study results show that: 1) The developing process of tunneling face deformation can be divided into 3 stages relating with expansion of soil plastic zone. 2) Compared to the case without hydraulic pressure, the stability of tunneling face accounting for fluid-solid coupling effect is significantly reduced; with the increase of water level and seepage time, the limiting supporting pressure to maintain stability increases gradually. 3) The support pressure is characterized by support pressure ratio; the reduction of the supporting pressure would induce the decrease of pore pressure at the front of tunneling face; the pore pressure near tunneling face is affected much more, which features funnel-shaped influence zone. 4) When collapse occurs to tunneling face, the significant settlements and soil displacement field of the ground would extend to ground level; and the horizontal displacement at the center of tunneling face correlates with the maximum ground settlement, showing parabolic correlation and linear correlation at different stages.

shield tunnel; stability of tunneling face; fluid-solid coupling; supporting pressure; ground deformation; pore pressure

2017-06-21;

2017-09-17

国家重点基础研究发展计划(973计划)项目(2015CB057800)； 国家重点研发计划(2016YFC0800204)

康志军(1991—)，男，四川凉山人，2017年毕业于同济大学，建筑与土木工程专业，硕士，现从事隧道及地下工程的设计工作。E-mail: demfemgeo@163.com。*通信作者： 谭勇， E-mail: tanyong21th@tongji.edu.cn。

10.3973/j.issn.1672-741X.2017.10.012

U 435

A

1672-741X(2017)10-1287-09