堆石防波堤不规则波浪反射系数试验研究

房 伟，陈国平，严士常，钟雄华，王 聪

(河海大学 港口海岸与近海工程学院，江苏 南京 210098)

堆石防波堤不规则波浪反射系数试验研究

房 伟，陈国平，严士常，钟雄华，王 聪

(河海大学 港口海岸与近海工程学院，江苏 南京 210098)

结合物理模型试验，分析斜坡坡度、波陡、相对水深、护面类型和破波参数等因素对堆石防波堤不规则波浪反射系数的影响规律。将常用的Van der Meer公式，Seelig公式，Postma公式和Davison公式计算值和实测值进行比较，并结合试验数据，基于有效波高和平均周期定义的Iribarren数，得出堆石防波堤不规则波浪反射系数经验公式。结果表明，该公式能较好地计算不规则波作用下块石和扭王块体护面堆石防波堤波浪反射系数。

不规则波；反射系数；堆石防波堤

堆石防波堤波浪反射特性是海岸工程设计的重要参数，其对于海底地形变化和港区内船舶航行和作业均有重要影响。许多学者对此展开理论分析和试验研究，取得一定成果。Miche[1]根据海滩坡度与波浪破碎特征，给出无量纲参数Miche数，认为反射系数与Miche数成正比。Battjes[2]采用Iribarren提出的破波参数(Iribarren数)完善Miche的理论，推导出光滑不透水斜坡的反射系数。Seelig和Ahrens[3]开展的试验显示Miche和Battjes公式均过高估计光滑斜坡的反射系数，并得出多种护面和不同渗透性的堆石防波堤不规则波浪反射系数与破波参数的经验公式。Postma[4]进行300多组不规则波试验，分别确定各因素对块石护面防波堤反射系数的影响，并给出反射系数计算公式。Davidson[5]等测量原型堆石防波堤的反射系数，提出表征各影响因素的无量纲参数R，该参数引入堤脚水深和护面块石特征直径两种因子，适合于包含涌浪和迎浪面较陡的情况。Van der Meer[6]和Zanuttigh基于大量试验数据研究多种护面，不同渗透性的堆石防波堤不规则波浪反射问题，提出反射系数经验公式。

以往研究成果主要考虑块石护面反射系数变化规律，对人工块体护面反射系数的研究相对较少，且主要以风浪为主，对波浪周期较长的涌浪研究有限。近年来，南海、非洲等以涌浪为主海域的海工工程建设发展迅速，涌浪作用下波浪爬高、越浪量、护面块体稳定性及波浪反射等特性与风浪有较大的差异。为此，本文在对已有研究成果分析的基础上，考虑斜坡坡度、入射波陡、相对水深、护面类型和破波参数等因素的影响，对单坡堆石防波堤波浪反射特性进行进一步研究，具有一定实际应用价值。

1 试验概况

波浪断面试验在波浪水槽中进行，该水槽可同时产生波浪、水流和风。水槽长86 m、宽1.0 m、深1.8 m。水槽的一端配有消浪缓坡，另一端配有二次反射吸收装置的推板式不规则波造波系统。模型按正态重力相似准则设计，结合波要素、试验断面和设备性能等因素确定模型长度比尺为1∶30。

试验不规则波波谱采用JONSWAP谱作为涌浪谱的近似，谱峰升高因子γ取3.3，波高采用电容式波高仪和DJ800多功能监测系统采集，采用连续造波方式，造波时间为1 800 s，相当于原型3 h。波浪反射由造波机自动吸收，采样间隔为0.05 s，每次采集1 600个波，每组波要素重复3次，试验组合如表1所示。

表1 试验组合Tab.1 Schemes of test

试验时在水槽中沿着波浪方向布置3根波高仪，并在中间排成一直线，同步测量模型前的波面数据。采用Mansard[7]推荐的三点法通过最小二乘法计算分离出入射波和反射波，并分析不规则波浪的反射系数。在堤前1倍入射波长以外，共设置了3根波高仪同时记录波面变化，相邻波高仪的间距分别取为1.0 m和0.8 m，第一根波高仪到建筑物前的距离取9.0 m。入反射波高仪的布置如图1所示。

图1 波高仪布置Fig.1 Layout of wave probe

试验断面海侧斜坡坡度取为1∶1.5、1∶2和1∶2.5，堤顶超高Rc为3.6 m，后侧坡度取为1∶1的自然坡。具体试验断面如图2所示。

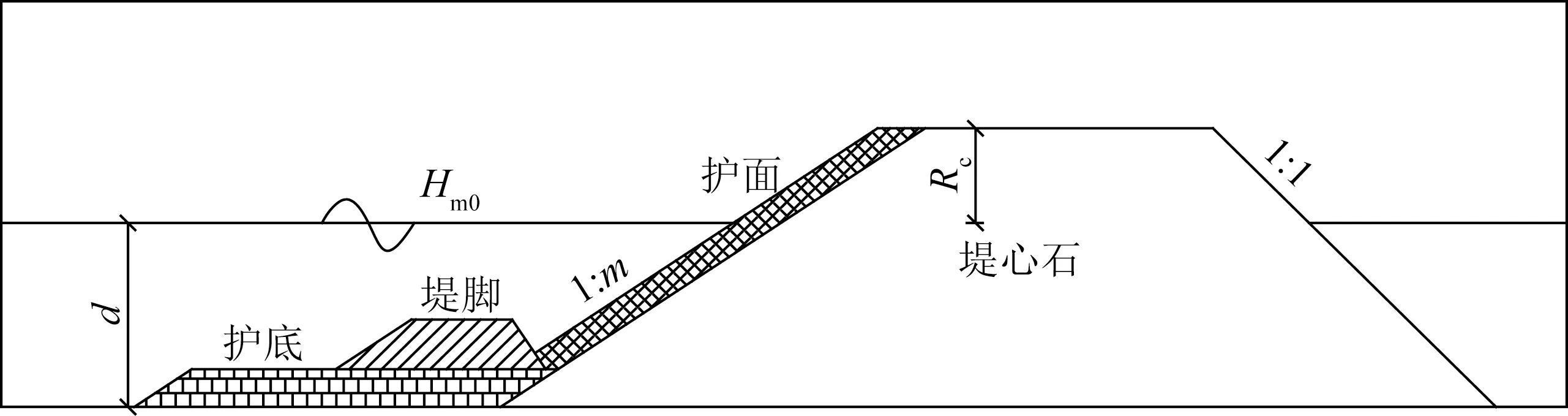
图2 试验断面示意Fig.2 Test section

试验断面堤心石采用1～1 000 kg开山石，护面采用300～1 350 kg块石或3 000 kg扭王块体，扭王块体随机摆放，堤心石和护面块石级配见表2。

表2 块石级配表Tab.2 Rock gradation

2 试验结果分析

波浪反射的程度以反射系数Kr表示，其由反射波高Hr和入射波高Hi或者反射波能量Er与入射波能量Ei定义[8]：

波浪反射主要取决于建筑物的特性、当地水深地形环境和来波条件，根据Battjes[2]的研究，堆石防波堤前波浪反射系数Kr与其主要影响因素之间关系可由如下函数式表示：

式中：α为斜坡坡度角，H为入射波高，L0为深水波长，d为试验水深。

本文针对块石和扭王块体两种护面形式，分别考虑斜坡坡度、入射波陡、相对水深、护面类型等因素对堆石防波堤不规则波浪反射系数的影响。

2.1波浪反射系数与斜坡坡度

迎浪面坡度是斜坡式堆石防波堤的重要参数，也是影响其波浪反射的主要因素之一。国内外防波堤常用坡度为1∶1.33～1∶3，在本次试验中分别采用1∶1.5、1∶2和1∶2.5三种坡度分析斜坡坡度的影响。由图3可知迎浪面坡度对波浪反射系数影响显著，即其它条件相同时，斜坡坡度越小，反射系数越小。这种现象是波浪在堆石防波堤斜坡上破碎剧烈程度随坡度减缓而迅速增加，同时当斜坡较缓时，波浪与斜坡面接触距离较长，波浪在此过程由于坡面摩阻消耗的能量亦同时增加，这些因素叠加作用使得波浪在坡度较小的斜坡上损耗的波能增加，同时由于堤顶超高Rc较大，堆石防波堤基本不越浪，从而传递至堤后的波能基本不变，故反射的波能减小，从而波浪反射系数减小。

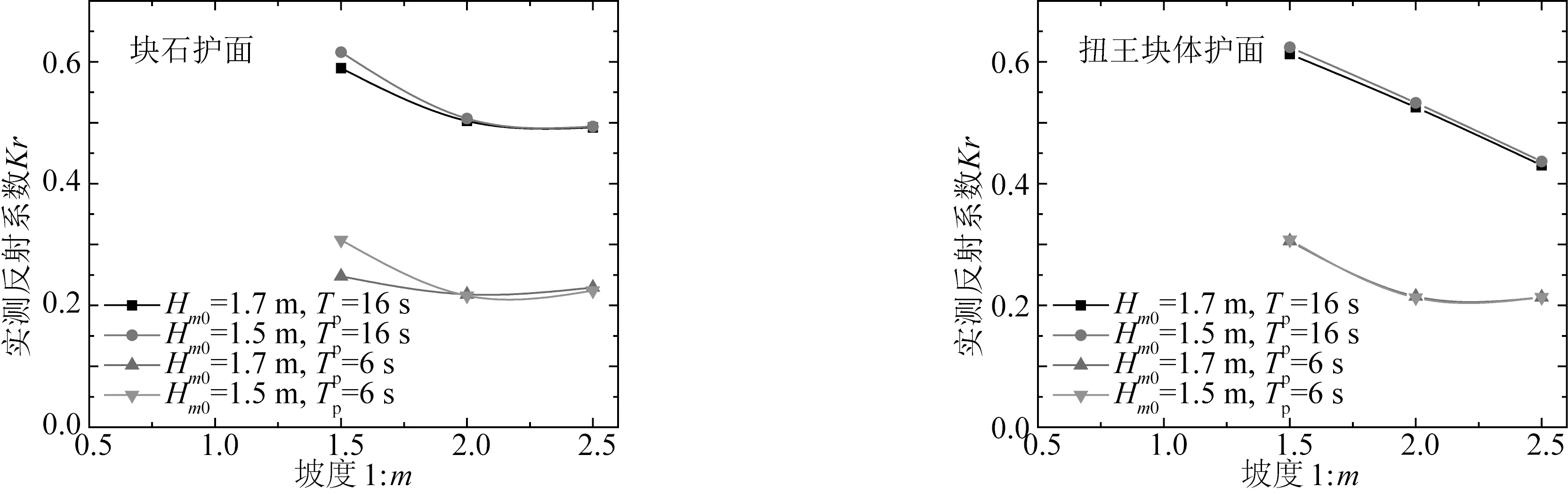
图3 实测反射系数随斜坡坡度变化Fig.3 Measured reflection coefficient with slope

2.2波浪反射系数与波陡

堤前来波条件，包括波高和周期对反射系数均有影响。在本次试验中采用波陡来表示两者综合作用效果，并采用基于堤脚处波高Hm0和理论深水波长L0的波陡s0=Hm0/L0来分析其影响。从图4可以看出，波陡对波浪反射系数有明显的影响，且波浪反射系数随着波陡的增大而减小。

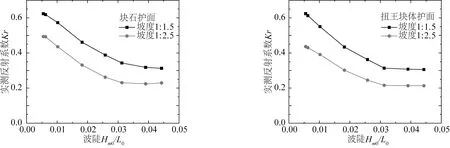
图4 实测反射系数随入射波陡变化Fig.4 Measured reflection coefficient with the incident wave steepness

这种规律是因为波浪传播到斜坡堤前，水深急剧减小，同时反射波浪和入射波浪叠加使得波高和波陡进一步增大，波浪容易发生破碎，对堆石防波堤产生冲击作用。当入射波波陡增大时，波浪到达堆石防波堤时更容易破碎，波浪能量被大量消耗，反射的波浪能量减小，波浪反射系数相应减小。故波浪反射系数会随着入射波陡的增大而减小。

2.3波浪反射系数与相对水深

在试验中通过模拟地形和改变堤前水深反映当地水深地形环境影响，同时本次试验中，波高水深比值较小，堤前入射波浪不破碎，并采用基于当地水深和理论深水波长的相对水深d/L0来分析其影响。

由图5可知，在堤前入射波浪不发生破碎时，堤前相对水深对反射系数的影响较小，且波浪反射系数随着相对水深的减小略有增大。这是因为相对水深较小时，波浪越浪量略有减小，波浪传递至堤后的能量略有减小，从而反射的波能较大，反射系数有所增大。

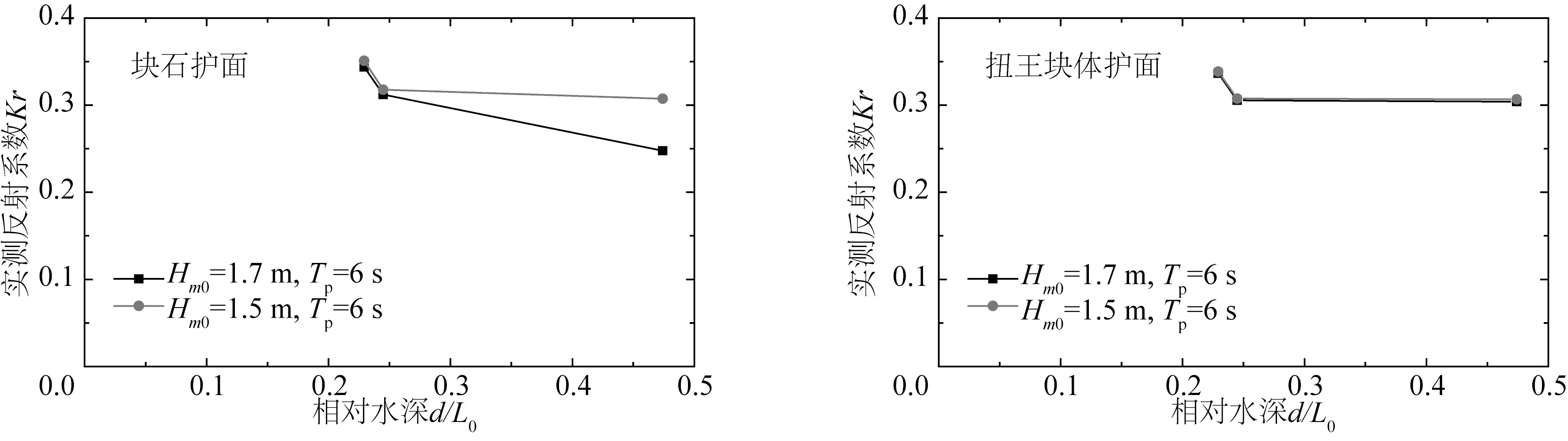
图5 实测反射系数随堤前相对水深变化Fig.5 Measured reflection coefficient with the relative depth

2.4波浪反射系数与护面类型

迎浪面是堆石防波堤与波浪直接作用区域，其护面类型的变化使得斜面上粗糙度和孔隙率不同，图6展现了三种坡度时，波浪反射系数随护面类型变化。从图6可知，对于块石护面和扭王块体护面的渗透堆石防波堤，由于扭王块体间孔隙较大，更多的波浪能量转化为孔隙间水流运动能量，使得反射波能较小，故波浪反射系数略有减小。

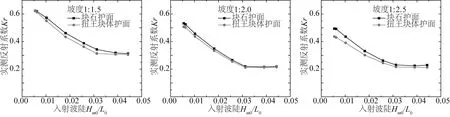
图6 护面类型对实测反射系数影响Fig.6 Measured reflection coefficient with the type of armour

2.5波浪反射系数与Iribarren数

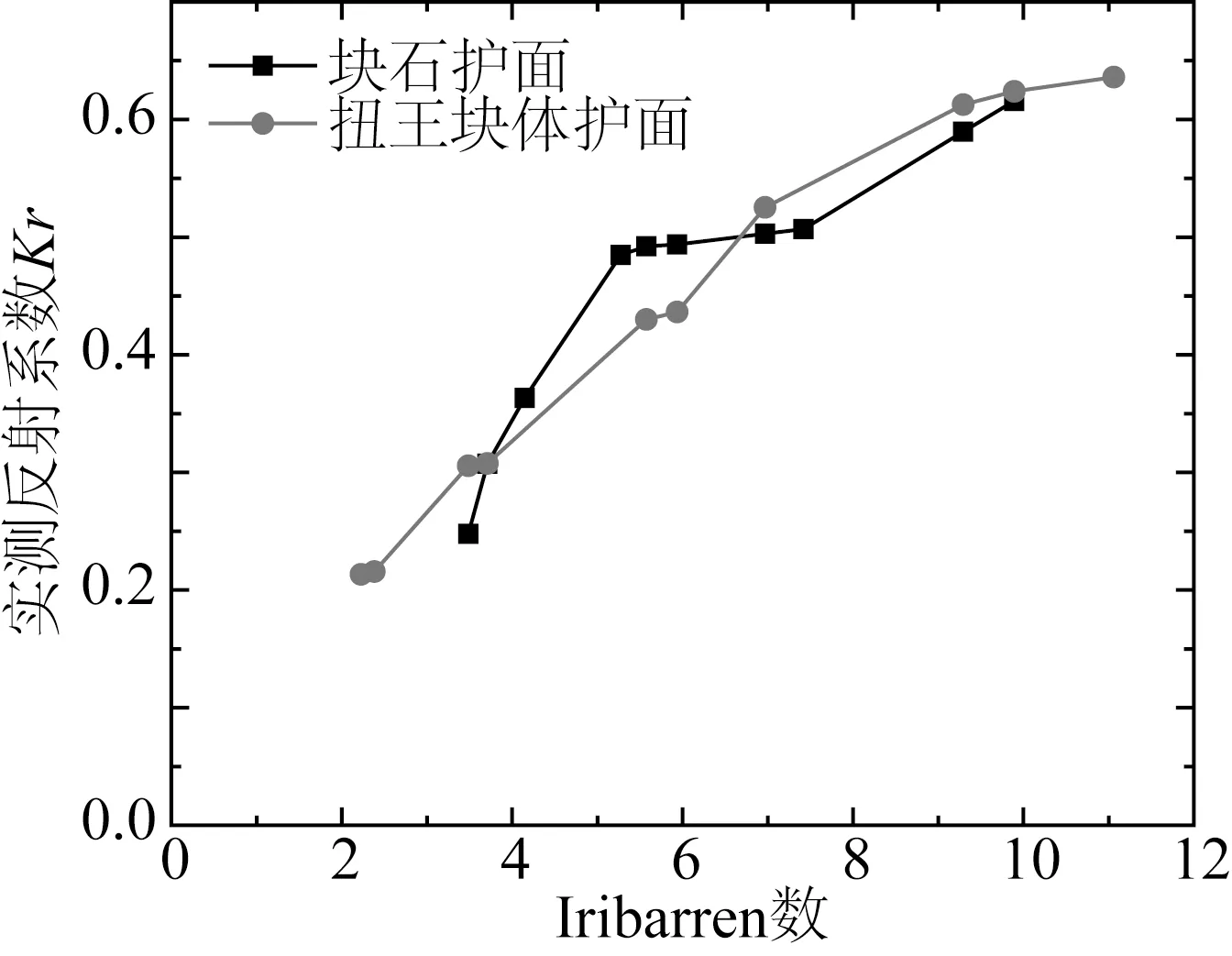
图7 实测反射系数与Iribarren数Fig.7 Measured reflection coefficient with Iribarren number

3 反射系数计算值与实测值比较

波浪反射能量与波浪在斜坡上破碎过程密切相关，在波浪透射和越浪较小时，波浪破碎会引起波浪能量耗散，波浪反射能量随之减小，Iribarren数能较好地反映出这些过程的特点，故Seelig公式和Van der Meer公式均采用Iribarren数表示各因素对波浪反射系数综合影响，得出反射系数经验关系为：

Van der Meer[6]和Zanuttigh首先定义斜坡堤堤脚处基于波浪谱的破波参数：

式中：tanα为斜坡坡度，Tm-1,0=m-1/m0，对于单峰谱，Tm-1,0=Tp/1.1，从而反射系数为：

式中：a，b均为经验参数，与斜坡的护面形式和渗透性有关。Van der Meer和Zanuttigh分析反射系数试验数据得出：对于块石和人工块体护面的渗透堤，a=0.12，b=0.87。

Seelig和Ahrens[3]结合模型试验结果给出一种反射系数与Iribarren数经验关系：

式中：a，b均为经验参数，根据Van der Meer[6]和Zanuttigh结果，对于块石和人工块体护面的渗透斜坡堤，a=0.75，b=15。Van der Meer公式和Seelig公式适用于：0.01≤s0≤0.07，Rc/Hm0≥0.5，1.5≤m≤2.0。

Postma[4]分别考虑斜坡坡度、入射波陡和渗透性对反射系数的影响，根据多元回归提出一种直接体现影响因素的公式：

式中：p是透水系数，反映斜坡堤整体渗透性，根据Van der Meer名义透水系数图取0.3；sop是基于有效波高Hs和谱峰周期Tp的波陡，α是迎浪面斜坡的坡度角。公式适用于：0.1≤p≤0.6，0.004≤sop≤0.05，0.7≤ξop≤8，1.5≤m≤6.0。

Davidson[5]等依据原型堆石防波堤反射系数，提出包含堤脚水深和护面块石特征直径的无量纲参数R，并提出块石护面的堆石防波堤反射系数公式：

式中：h为堤脚处水深，Dn50为护面中值粒径，Hi为入射波高，L0为入射波长，α为坡度角，公式应用范围：6.4≤ξ≤23.1，0.64≤m≤1.23。

图8展示了四种常用公式得出的反射系数计算值与实测值的比较，斜线为45°线。对于块石和扭王块体护面，两者反射系数比较接近。Van der Meer公式，Seelig公式和Postma的公式在Iribarren数较小时，均与实测反射系数接近；但在Iribarren数较大时，Seelig公式，Van der Meer公式计算值与实测值吻合较好而Postma公式计算值与实测值有一定的偏差，Davidson公式计算值则较实测值总体偏小。

图8 反射系数实测值与计算值比较Fig.8 Calculated reflection coefficient with measured values

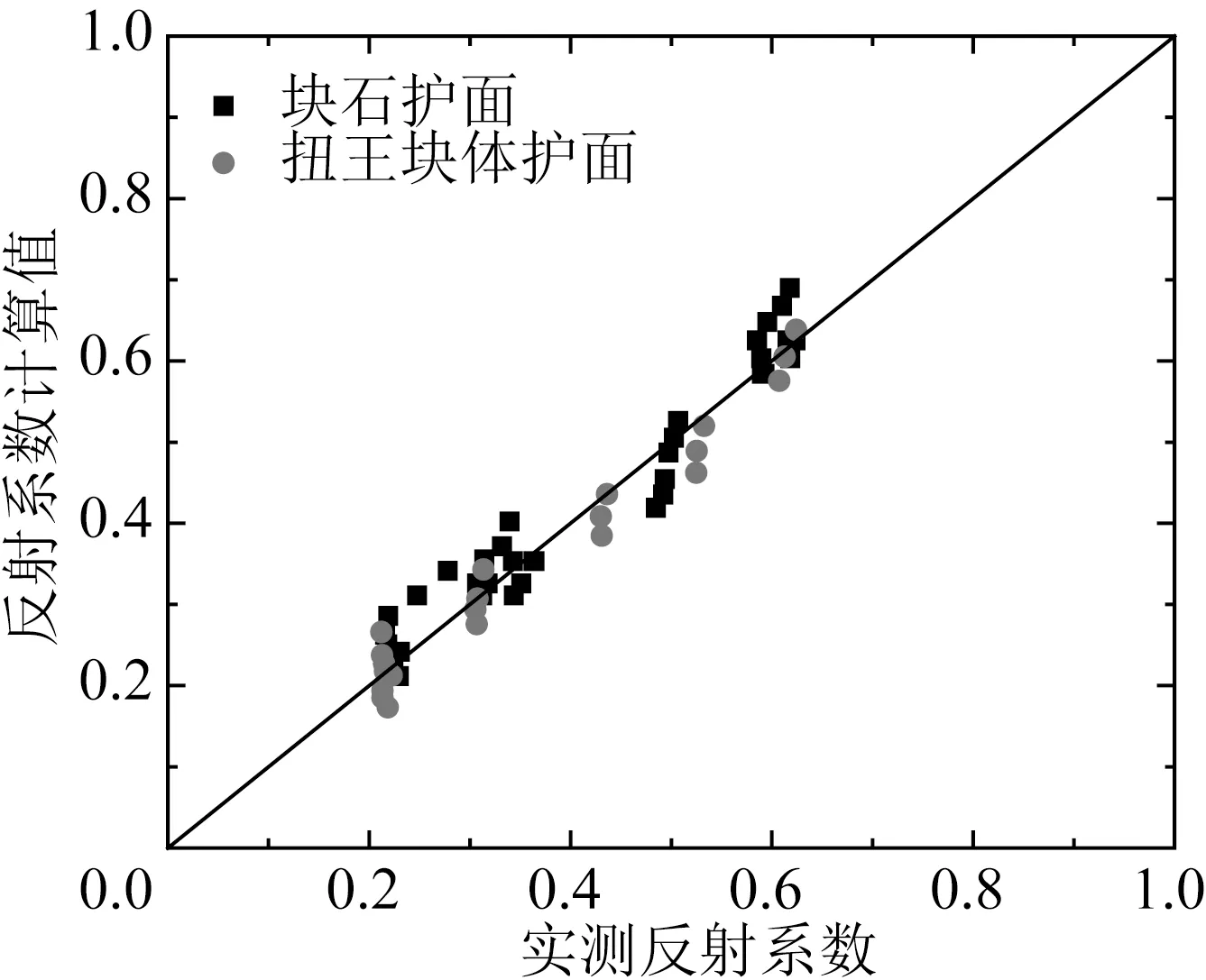
图9 实测值与拟合公式计算值比较Fig.9 Comparison of measured and fitted values

为进一步推求反射系数与护面结构关系，基于常用的有效波高Hs和平均周期T定义Iribarren数，依据实测数据和Van der Meer公式结构，拟合出反射系数经验公式：

式中：对于块石护面的渗透斜坡堤，a=0.12，b=0.79；对于扭王块体护面的渗透斜坡堤，a=0.10，b=0.94。公式适用于：1.5≤m≤2.5,0.006≤s≤0.05，3.5≤ξ≤10.0以及Rc/Hs≥1.9。

将经验公式计算值与反射系数实测值比较结果绘于图9，对于块石护面情况，计算值与实测值相关系数为0.971，对于扭王块体护面的情况，计算值与实测值相关系数为0.983，两者反射系数计算值与实测值吻合较好。

4 结 语

探讨了斜坡坡度、波陡、相对水深、护面类型和破波参数等因素对斜坡式堆石防波堤反射系数的影响规律，对常用波浪反射系数计算公式进行比较分析，结合试验数据拟合反射系数经验公式，得出以下结论：

1)堆石防波堤不规则波反射系数主要与斜坡坡度和入射波波陡有关，入射波在堤前不发生破碎时，相对水深对反射系数影响较小，护面类型对反射系数有一定的影响；

2)堆石防波堤不规则波反射系数与Iribarren数密切相关，反射系数随着Iribarren数的增大而增大；

3)结合实测波浪反射系数可知，Seelig公式和Van der Meer公式计算值与实测值吻合较好；

4)采用常用的有效波高Hs和平均周期T定义Iribarren数，基于该参数得出的经验公式能较好地计算不规则波作用下块石和扭王块体护面堆石防波堤波浪反射系数。

[1] MICHE M.Le pouvoir reflêchissant des ouvrages martimes exposés à l’action de la houle[J].Ann Ponts Chaussées,1951,121: 285-319.

[2] BATTJES J A.Surf similarity[C]//Proceedings of the XIV Int.Conf.Coastal Eng.ASCE.1974: 466-480.

[3] SEELIG W N,AHRENS J P.Estimation of wave reflection and energy dissipation coefficients for beaches,revetments and breakwaters[R].CERC Technical paper 81-1,Fort Belvoir,U.S.A.C.E.MS,Vicksburg,1981.

[4] POSTMA G M.Wave reflection from rock slopes under random wave attacks[D].Delft: Delft University of Technology,1989.

[5] DAVIDSON M A,BIRD P A D,BULLOCK G N,et al.A new non-dimensional number for the analysis of wave reflection from rubble mound breakwaters[J].Coastal Eng.,1996,28:93-120.

[6] ZANUTTIGH B,VAN DER MEER J W.Wave reflection from coastal structures in design conditions[J].Coastal Eng.,2008,55:771-779.

[7] MANSARD E P D,FUNKE E R.On the reflection analysis of irregular waves[R].Natl.Res.Counc.Rev.Can.Hydraulics Laboratory Technical Report,1987: TR-HY-O17.

[8] The rock manual[M].London: CIRIA,2007:520-523.

[9] 邵利民.入、反射波浪的分离与反射系数的研究[D].大连: 大连理工大学,2003.(SHAO L M.Separation of incident waves and reflected waves and study of reflection coefficients[D].Dalian: Dalian University of Technology,2003.(in Chinese))

Experimental research of wave reflection coefficient on rubble mound breakwaters under irregular waves

FANG Wei,CHEN Guoping,YAN Shichang,ZHONG Xionghua,WANG Cong

(College of Harbour,Coastal and Offshore Engineering,Hohai University,Nanjing 210098,China)

Based on the physical model experiment,the influence of slope,wave steepness,relative water depth,the type of armour and wave breaking parameters on the wave reflection coefficient of rubble mound breakwaters is analyzed.And the measured reflection coefficient is compared with the commonly used Van der Meer formula,Seelig formula,Postma formula and Davidson formula.And an empirical formula of wave reflection adopted with the Iribarren number defined by effective wave height and average period is fitted with the experimental data.The results show that the formula can calculate the wave reflection coefficient well.

irregular waves; wave reflection coefficient; rubble mound breakwaters

TV139.2

A

10.16483/j.issn.1005-9865.2017.05.015

1005-9865(2017)05-0125-07

2017-01-10

房伟(1993-)，男，硕士研究生，从事波浪与建筑物相互作用研究。E-mail:hohaifangwei@163.com