内陆水体水质参数遥感反演集合建模方法

曹 引,冶运涛,赵红莉,蒋云钟,王 浩,王俊锋



内陆水体水质参数遥感反演集合建模方法

曹 引1,2,冶运涛2*,赵红莉2,蒋云钟2,王 浩1,2,王俊锋1

(1.东华大学环境科学与工程学院,国家环境保护纺织工业污染防治工程技术中心,上海 201620；2.中国水利水电科学研究院,流域水循环模拟与调控国家重点实验室,北京 100038)

以微山湖为研究对象,利用2015年6月11~13日获取的实测高光谱和水体叶绿素a浓度、总悬浮物浓度和浊度数据,构建3种水质参数遥感反演常用的经验模型和PSO-SVM模型并进行精度评价,确定参与3种水质参数集合建模的反演模型,分别利用以熵权法(EW-CM)、集对分析法(SPA-CM)为代表的确定性集合建模方法和以贝叶斯模型平均(BMA)为代表的概率性集合方法构建反演3种水质参数的EW-CM、SPA-CM和BMA集合模型.通过贝叶斯平均方法获取各模型和BMA集合模型反演3种水质参数的不确定性区间,对比3种水质参数各模型和集合模型反演结果.结果表明:(1)确定性集合模型中SPA-CM模型精度整体高于EW-CM模型;(2)BMA概率性集合模型建模精度整体上要优于SPA-CM和EW-CM集合模型,验证精度稍低于SPA-CM模型,和EW-CM模型相当;(3)概率性集合建模可以给出集合模型和各模型反演水质参数的不确定性区间;(4)确定性和概率性集合模型可以综合各模型信息,使得集合模型同时具有较高的建模和验证精度,降低单一模型反演水质参数的不确定性,并在一定程度上提高水质参数反演精度.

内陆水体；水质遥感；集合建模；微山湖；叶绿素a；总悬浮物；浊度

目前,从事内陆水质遥感相关研究的学者提出以水体叶绿素a浓度、总悬浮物浓度和浊度等水质参数为主要监测对象的众多遥感反演模型,由于内陆水体光学特征的复杂性,不同遥感反演模型随内陆水体的时空变化呈现不同的适用性,目前还没有普适性的水质遥感反演模型[1].现阶段用于水质反演的经验模型、分析模型和机器学习模型在不同时间、不同水体、不同遥感数据源以及不同水质参数反演中的表现具有显著差异[2-9],各模型反演能力均存在一定的局限性,使得模型选择具有不确定性.而集合建模可以通过赋予各模型不同权重将不同模型集合,可以综合各模型信息,提高模型的稳定性,并在一定条件下提高水质参数反演精度[10].

集合建模是指通过集合方法确定各模型权重,将各模型模拟值进行加权求和,进而综合各模型信息的一种建模方法.集合建模思想常用于水文预报,在水质遥感领域的应用鲜有报道.集合建模的关键在于集合方法的选择,即各模型权重的确定方法.目前有关集合建模权重确定的方法主要有5种: (1)利用各模型的相对误差来确定权重,相对误差越小其权重越大,主要有熵权法[11]和集对分析法[12];(2)将各模型权重计算转化为非线性优化问题,基于目标函数和约束条件采用优化算法求解,如遗传算法[13]和粒子群算法[14];(3) 根据各模型预测值和实测值,利用神经网络等多元回归模型来构建各模型预测值和实测值之间的关系,达到集合建模的目的[15];(4) 基于数据同化思想推导权重计算公式,利用均方根误差来确定权重[16];(5) 基于贝叶斯理论,利用贝叶斯模型加权平均(BMA)方法来确定权重,获取预测变量的最优估计,并且可以获取预测变量的不确定性区间[17-18],因此,称该方法为概率性集合方法,相应称(1)-(4)为确定性集合方法.确定性集合建模方法中,熵权法和集对分析法相对简单,易于实现.本文以南水北调东线重要水源地南四湖最大湖泊微山湖为研究区,构建微山湖水体叶绿素a浓度、总悬浮物浓度和浊度常用的经验模型和支持向量机(SVM)模型,引入集合建模思想,选择以熵权法和集对分析法为代表的确定性集合方法和以贝叶斯平均为代表的概率性集合方法研究微山湖3种水质参数遥感集合建模方法,以期提高水质参数反演精度,降低水质参数遥感反演的不确定性.

1 研究方法

1.1 确定性集合建模方法

1.1.1 基于熵权法的集合建模方法 集合建模关键在于各模型权重的确定,基于熵权法的集合建模(EW-CM)利用各模型反演采样点处水质参数的相对误差e(式(1))计算各模型相对误差权重P()熵值H(式(2)、式(3)),利用熵值计算各模型误差变异程度系数D(式(4)),最后确定各模型权重(式(5)),构建反演水质参数EW-CM集合模型(式(6))[10].

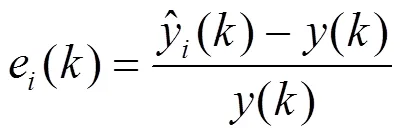
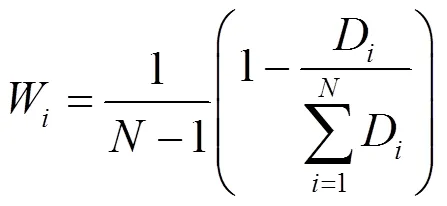
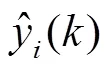
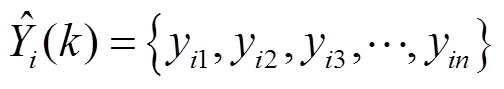
将三元联系度转换成联系数,进而求出各模型的相对隶属度v.根据相对隶属度确定各模型权重W,建立反演水质参数的SPA-CM集合模型:

v=1/+1/×¢(8)

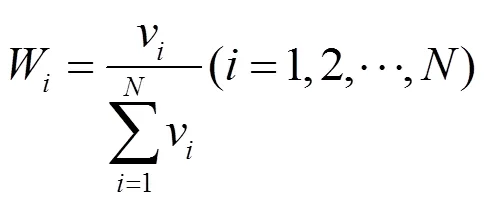
1.2 概率性集合建模方法

1.2.1 贝叶斯模型加权平均 贝叶斯模型加权平均(BMA)方法基于贝叶斯理论确定各模型权重和误差,实现多模型集合建模,并能提供各模型和集合模型反演不同样点处水质参数的不确定区间.BMA集合建模思路如下[17]:

假设为待反演水质参数,=[,]为实测数据(其中表示实测光谱反射率,表示实测水质参数),=[1,2,×××,y]为个模型水质参数反演值的集合.BMA的集合反演表示如下:

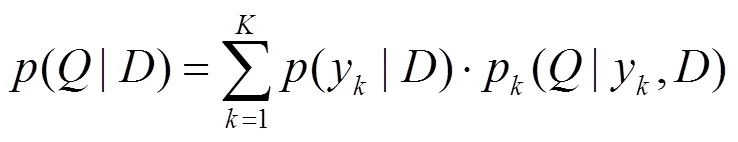
利用权重对各模型水质参数反演值进行加权求和,得到BMA集合模型水质参数反演值.如果各模型对水质参数的反演值和水质参数的实测值均服从正态分布,则BMA集合模型反演值可利用式(12)计算:

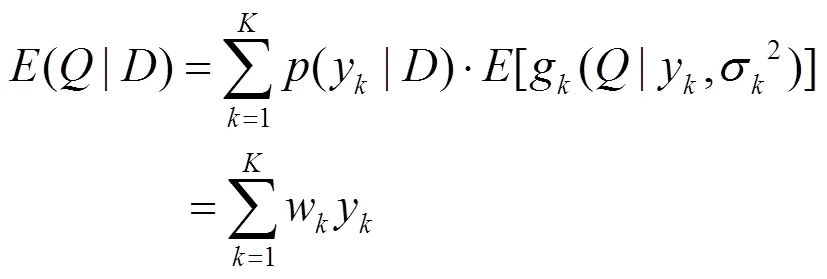
1.2.2 期望最大化算法 期望最大化(EM)算法是一种计算BMA集合模型中各模型权重的方法[19].EM算法要求各模型对水质参数的反演值和水质参数的实测值均服从正态分布,因此,在用EM算法计算各模型权重前,首先对水质参数的实测值和反演值进行正态检验,若不符合正态分布,则利用Box-Cox函数对水质参数的实测值和反演值进行正态转换.EM算法的详细过程参考文献[17].

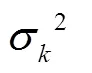
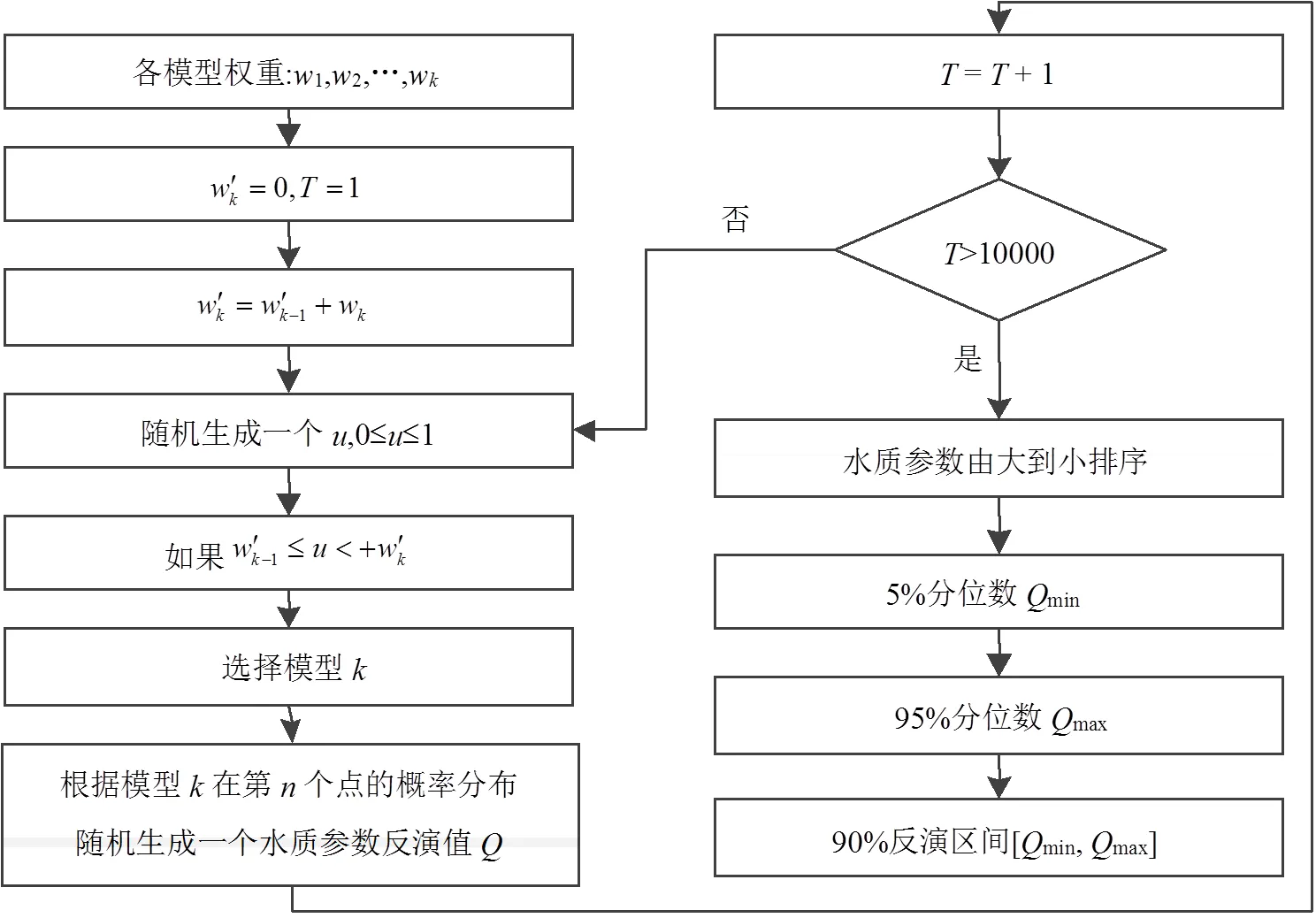
图1 水质参数浓度区间反演流程

2 数据和模型

2.1 数据获取

图2 2015年6月份采样点分布

微山湖位于济宁市微山县境内,地处苏鲁边界结合部,为内陆湖泊南四湖中面积最大的一个湖泊,水面面积531.17km2,是全国著名的淡水湖之一.微山湖是南水北调东线工程重要的湖泊水源地,具有防洪、排涝、灌溉、供水、养殖及旅游等多种功能.2015年6月12~13日在微山湖布设41个采样点(图2),进行实地光谱采集和同步水质取样.利用SVC公司生产的HR-1024地物光谱辐射计采用水面以上倾斜测量法采集光谱[20-21];水体取样后冷藏,于24h内送至实验室,用醋酸纤维膜过滤,放置于90%丙酮中萃取,再将萃取液放置冰箱中遮光冷藏24h,用UV-2550分光光度计测量叶绿素a浓度.总悬浮物浓度测定按照国家标准GB 11901-89[22],采用过滤烘干法,先将滤膜置于105℃烘箱中烘干2h,除去水分并称重1,用称重后的滤膜过滤100mL水样后于105℃烘干2h再次称重2,两次重量相减(2-1)除以过滤水样体积,即求得总悬浮物质量浓度,=(2-1)/.浊度用美国哈希HACH浊度仪1900C现场测量.剔除一个光谱异常点,保留剩余40个点,其中28个点用于建模,12个点用于验证,其中建模数据中包含叶绿素a浓度、总悬浮物浓度和浊度极值,模型反演时内插精度往往高于外推,2015年6月微山湖水质参数统计情况见表1,40个样点光谱曲线如图3所示.

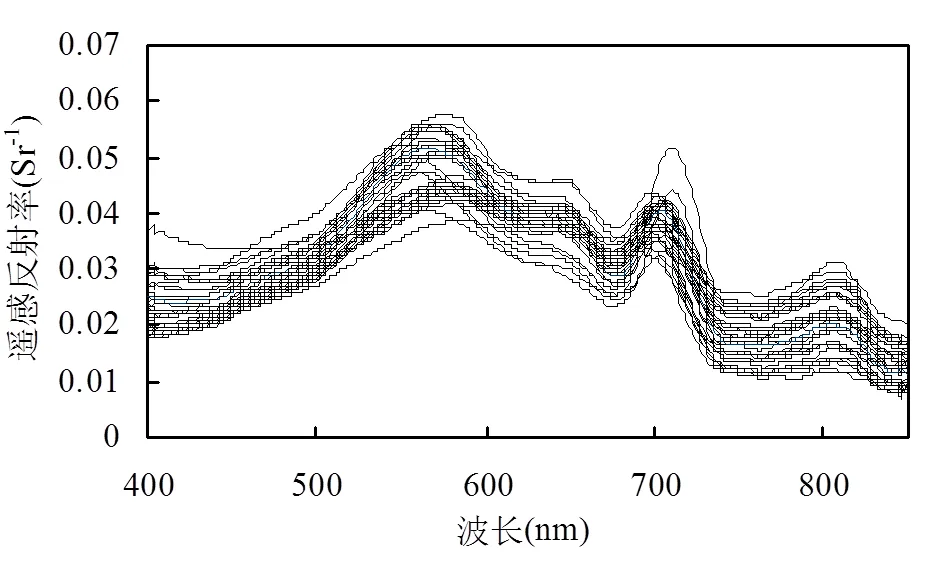
图3 采样点水体光谱曲线

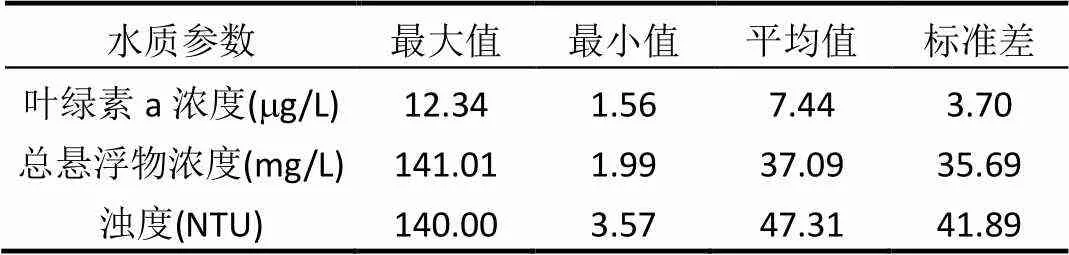
表1 2015年6月微山湖水质参数统计表

2.2 水质参数反演模型构建

选择水体叶绿素a浓度、总悬浮浓度和浊度反演常用的经验模型和支持向量机模型作为集合反演备选模型集,其中3种水质参数反演模型集如表2所示.单波段模型和一阶微分模型分别利用400~850nm归一化光谱反射率 (式(13))、一阶微分光谱反射率(用¢()表示处一阶微分光谱反射率)和3种水质参数进行相关分析,选择和水质参数相关性最好的特征波段构建模型;波段比值模型分别利用400~850nm原始光谱反射率、归一化光谱反射率两两比值,选择和3种水质参数相关性最好的原始光谱反射率比值和归一化光谱反射率分别建立波段比值模型;叶绿素a浓度三波段、四波段模型、总悬浮物浓度和浊度统一模式构建原理分别参考文献[23-25];上述模型仅利用了400~850nm波段范围内有限几个波段的光谱反射率,而偏最小二乘模型(PLS)可以充分利用多个波段的光谱信息,首先利用小波变换[26]对光谱去噪,在此基础上利用改进的离散粒子群优化算法(NDBPSO)优选3种水质参数多个特征波段和特征变量,构建NDBPSO-PLS模型,具体过程参考文献[27];支持向量机模型构建采用PSO算法优选惩罚系数和核参数,利用光谱反射率构建PSO- SVM模型,具体参考文献[28].

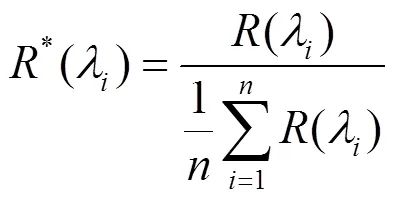
式中:R()和()分别为波长处的归一化光谱反射率和光谱反射率,∈[400~850nm];为400~850nm范围内的波段个数.

表2 水体叶绿素a浓度、总悬浮浓度和浊度反演模型集

2.3 模型精度评价

模型精度由建模和验证精度同时决定.模型精度用相对均方根误差、平均相对误差、综合误差以及模型决定系数2来衡量.相关计算公式如下:

(1)均方根误差RMSE:

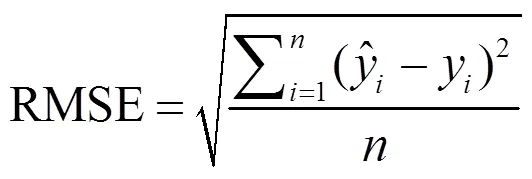
(2)相对均方根误差rRMSE:

(3)相对误差ARE:

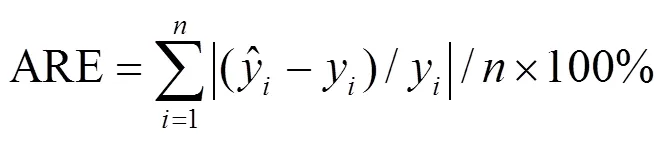
(4)综合误差CE:

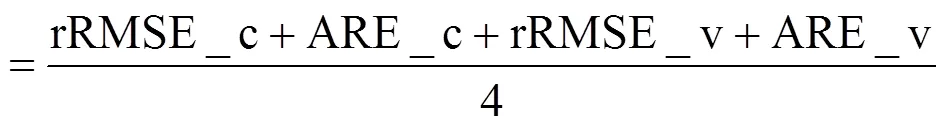
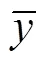
3 结果与讨论

3.1 集合模型选择

利用2015年6月12~13日在微山湖获取的水体叶绿素a浓度、总悬浮物浓度和浊度以及同步获取的水体高光谱数据,依次构建表2中3种水质参数反演模型集,其中叶绿素a浓度和三波段、四波段的相关系数偏低无法建模,对3种水质参数的各反演模型进行精度评价.叶绿素a浓度反演模型集中的一阶微分模型、总悬浮物浓度反演模型集中的单波段模型、统一模式和NDBPSO -PLS模型以及浊度反演模型集中的单波段反演模型、统一模式综合误差均较大,不参与集合建模.最终参与集合建模的3种水质参数反演模型及其精度如表3、表4和表5所示.

由表3可以看出,叶绿素a浓度4种反演模型中*692.1nm单波段模型、696.2nm401.9nm波段比值模型和基于特征波段的NDBPSO-PLS模型的2和建模综合误差差别较小,模型2均在0.78~0.8之间,建模误差介于26%~28%之间; PSO-SVM模型2显著高于前3种模型,2达0.90,建模综合误差仅为14.77%,PSO-SVM模型模拟光谱特征和水质参数之间这种复杂的非线性关系具有显著优势,但其验证综合误差较经验模型要大,模型反演能力偏低,存在过拟合的风险.由表4可以看出,总悬浮物浓度反演模型中PSO- SVM模型建模精度最高,但验证综合误差最大,一阶微分模型建模精度最差,但验证精度最高,由此可见,模型的建模和验证精度存在不一致性.由表5可以看出,浊度5种反演模型中PSO-SVM模型同时具有最高的建模和验证精度,模型综合误差最小;688nm568.2nm波段比值模型和NDBPSO-PLS模型建模2最大,达到0.95以上,但建模误差和*684nm单波段模型、¢585.6nm一阶微分模型较为接近,建模2和建模综合误差之间无单调关系.综上所述,不同水质参数的不同反演模型建模和验证精度往往存在较大差异,两者难以一致,使得只利用单一模型进行水质参数反演充满了不确定性.

3.2 确定性集合模型构建

分别利用熵权法和集对分析法获取反演3种水质参数的各模型权重,构建EW-CM和SPA- CM集合模型,各模型权重和集合模型精度评价如表3、表4和表5所示.

由表3可以看出,叶绿素a浓度各反演模型中,PSO-SVM模型具有最高建模2和最低建模误差,基于特征波段的NDBPSO-PLS模型具有最高验证精度,验证误差为24.54%;叶绿素a浓度EW-CM和SPA-CM集合模型建模2分别为0.84和0.85,高于单波段模型、波段比值模型和NDBPSO-PLS模型,仅低于建模精度最高的PSO-SVM模型;建模误差分别为22.99%和22.13%,仅高于建模误差最小的PSO-SVM模型;验证误差分别为27.55%和27.66%,仅高于验证误差最小的NDBPSO-PLS模型、EW-CM和SPA-CM集合模型;综合误差分别为25.27%和24.89%,仅低于综合误差最小的PSO-SVM模型.可以看出,叶绿素a浓度EW-CM和SPA-CM集合模型建模2、建模精度和验证精度均仅次于表现最佳的模型,集合模型集合了各模型信息,建模和验证精度具有一致性,降低了模型反演水质参数的不确定性;综合对比叶绿素a浓度EW- CM和SPA-CM集合模型,SPA-CM集合模型整体上要优于EW-CM集合模型.

由表4可以看出,总悬浮物浓度各反演模型中,688nm568.2nm波段比值模型具有最高建模2和最低建模误差,¢585.6nm一阶微分模型验证误差最低;总悬浮物浓度EW-CM和SPA-CM集合模型建模2、建模误差分别为0.97、19.17%和0.98、16.47%,建模精度仅次于PSO-SVM模型,验证综合误差分别为39.43%和38.97%,低于所有模型,集合模型在验证精度上得到一定程度的提高;综合对比总悬浮物浓度EW-CM和SPA- CM集合模型,SPA-CM集合模型整体上要优于EW-CM集合模型.

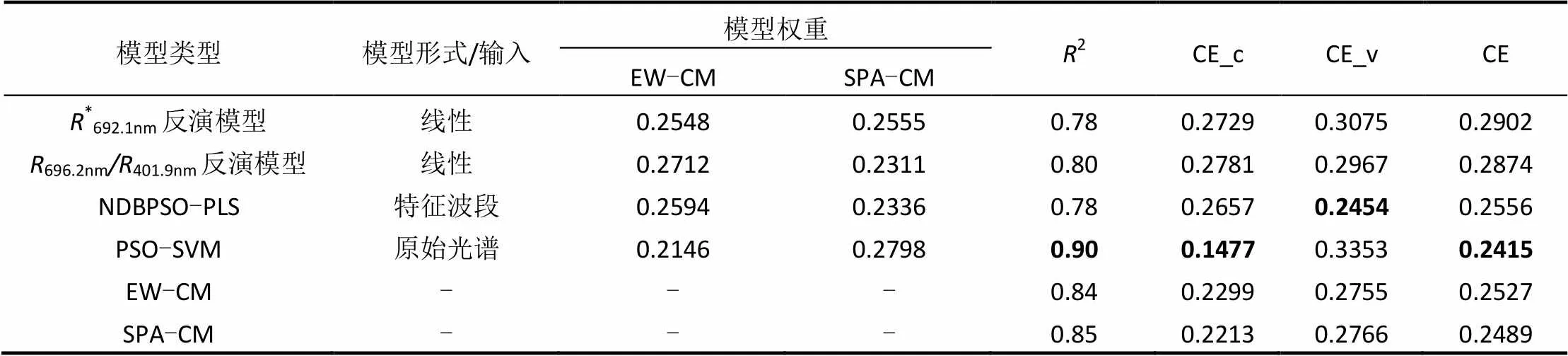
表3 叶绿素a浓度反演模型集

注:*代表归一化反射率;¢代表一阶微分光谱反射率;_c代表建模,_v代表验证,-代表无对应属性, 加粗代表最优属性,下同.

表4 总悬浮物浓度反演模型集

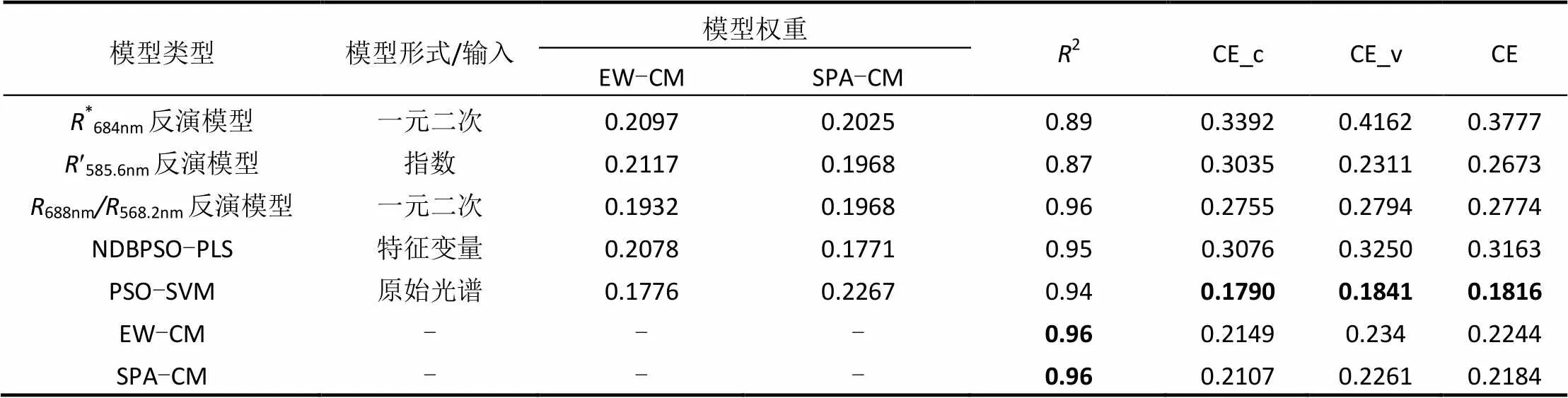
表5 浊度反演模型集

由表5可以看出,浊度各反演模型中688nm/568.2nm波段比值模型和NDBPSO-PLS模型具有最高建模2,2达0.95以上,且2种模型误差和验证误差相近,PSO-SVM建模和验证误差具有相似特点,且建模和验证误差均小于其他模型,模型精度最高;浊度EW-CM和SPA-CM集合模型建模2高于所有模型,拟合精度得到一定程度提升,两种集合模型建模和验证误差接近,仅高于PSO-SVM模型,且差异较小,显著高于其他模型;若各模型中存在建模和验证精度同时优于其他模型的模型,则该模型可作为最佳模型,此时集合模型在建模和验证精度的提升上有限.

3.3 概率性集合反演构建

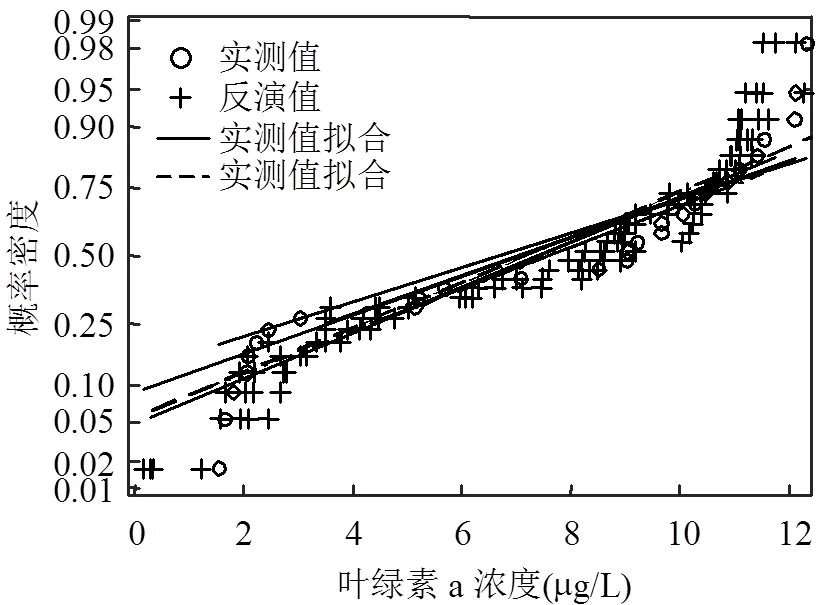
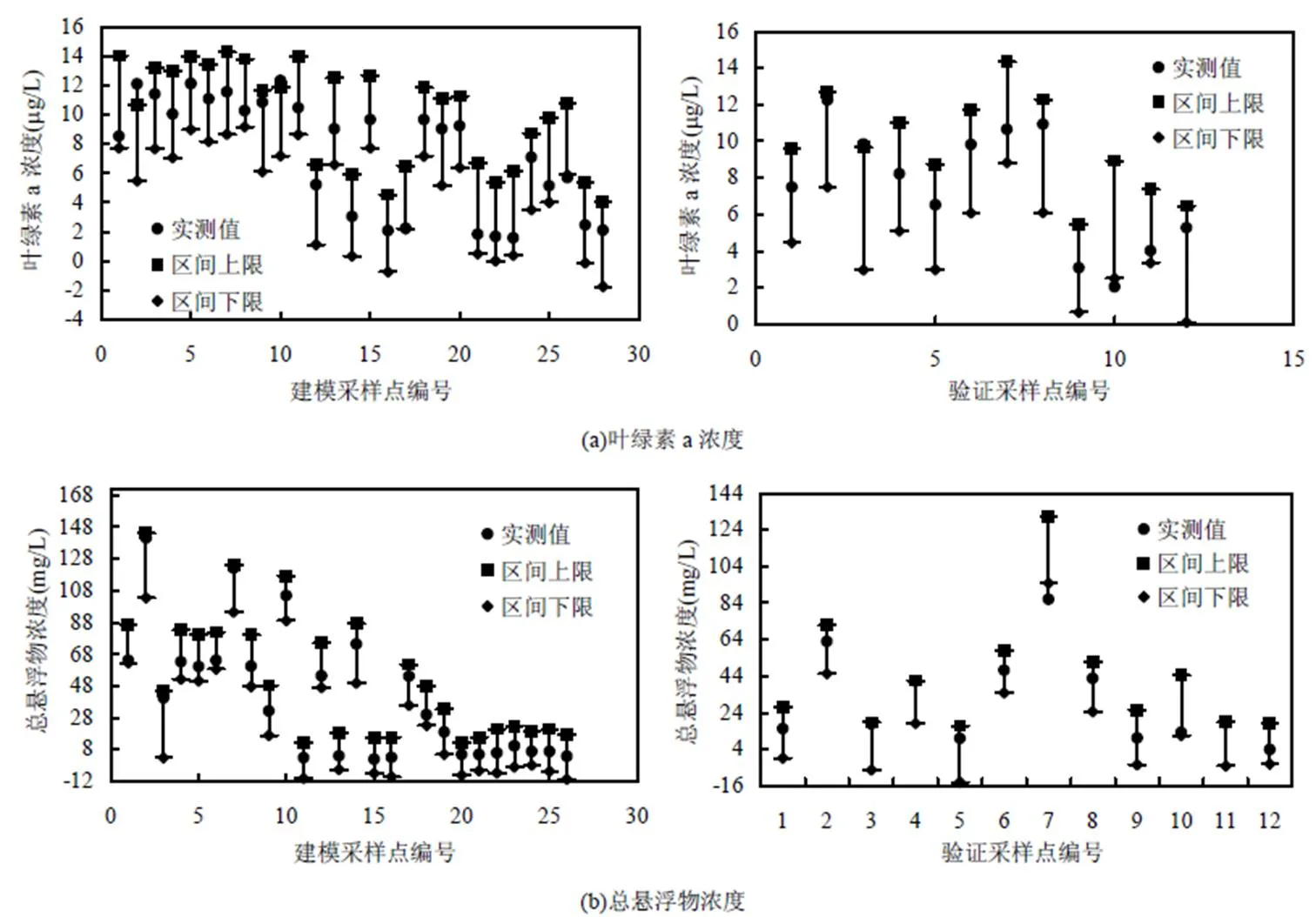
首先检验3种水质参数实测值和各模型反演值分布的正态性,绘制其概率分布图(图4),由图4可以看出3种水质参数实测值和反演值的正态概率图接近一条直线,可以定性判定3种水质参数实测值和反演值接近正态分布.同时利用Jarque-Bera定量检验其正态性,3种水质参数均通过正态性检验(返回值=0).在此基础上,利用期望最大化算法迭代计算3种水质参数BMA集合模型中各模型权重,对集合模型进行精度评价,同时计算集合模型和各模型反演3种水质参数的90%不确定性区间,本文仅显示BMA集合模型反演3种水质参数的90%不确定性区间(图5),分别计算集合模型和各模型反演3种水质参数的覆盖率、区间宽度和平均偏移幅度[17],结果分别见表6、表7和表8.

由表6可以看出,叶绿素a浓度BMA集合模型建模2为0.86,仅次于建模2最高的PSO-SVM模型,显著高于其他3种模型的建模2;建模综合误差和建模2类似,高于PSO-SVM模型,低于其他3种模型,验证综合误差仅高于NDBPSO-PLS模型;可以发现集合模型无论建模2、建模综合误差和验证综合误差都最大程度接近最优模型.对比分析BMA集合模型和各模型获取的叶绿素a浓度90%不确定性区间的覆盖率、平均带宽和平均偏移幅度,BMA集合模型建模和验证90%不确定性区间对实测值的覆盖率分别为89.29%和83.33%,均和覆盖率最高的模型持平;建模90%不确定性区间平均带宽PSO-SVM模型最小,BMA集合模型和其他3种模型差异较小;建模90%不确定性区间平均偏移幅度PSO-SVM模型最小,BMA集合模型和其他3种模型比较接近,验证90%不确定性区间平均偏移幅度BMA集合模型小于各模型,区间对称性较好,集合建模可一定程度上提高水质参数反演的稳定性.

由表7可以看出,总悬浮物浓度BMA集合模型建模2为0.98,和建模2最大的PSO-SVM模型十分接近,建模精度仅低于PSO-SVM模型,显著高于其他两个模型,验证精度高于各模型,集合模型一定程度上提高了总悬浮物浓度反演精度.对比分析BMA集合模型和各模型获取总悬浮物浓度90%不确定性区间的覆盖率、平均带宽和平均偏移幅度,BMA集合模型建模不确定性区间覆盖率高于各模型,验证不确定区间覆盖率和覆盖率最高的模型持平,具有较高覆盖率的同时具有较大的平均带宽;总悬浮物浓度BMA集合模型90%不确定性区间的平均偏移幅度和叶绿素a浓度反演类似,建模不确定性区间平均偏移幅度小于PSO-SVM模型,和其他3种模型之间的差异较小,验证不确定性区间平均偏移幅度小于各模型,集合建模可一定程度上提高水质参数反演的稳定性.

由表8可以看出,浊度BMA集合模型建模2达0.96,高于所有模型,建模和验证误差仅大于误差最小的PSO-SVM模型.BMA集合模型和各模型获取浊度90%不确定性区间的覆盖率、平均带宽特征和总悬浮物浓度BMA集合模型类似,具有较高覆盖率的同时具有较大的平均带宽;建模不确定性区间平均偏移幅度低于PSO-SVM模型,验证不确定性区间仅高于PSO-SVM模型.由于浊度PSO-SVM反演模型同时具有最小的建模和验证误差,此时集合模型对浊度建模和验证精度的提高有限,但从获取的90%不确定性区间特征来看,集合建模可一定程度提高区间覆盖率,降低平均偏移幅度,提升模型反演的稳定性和可靠性.

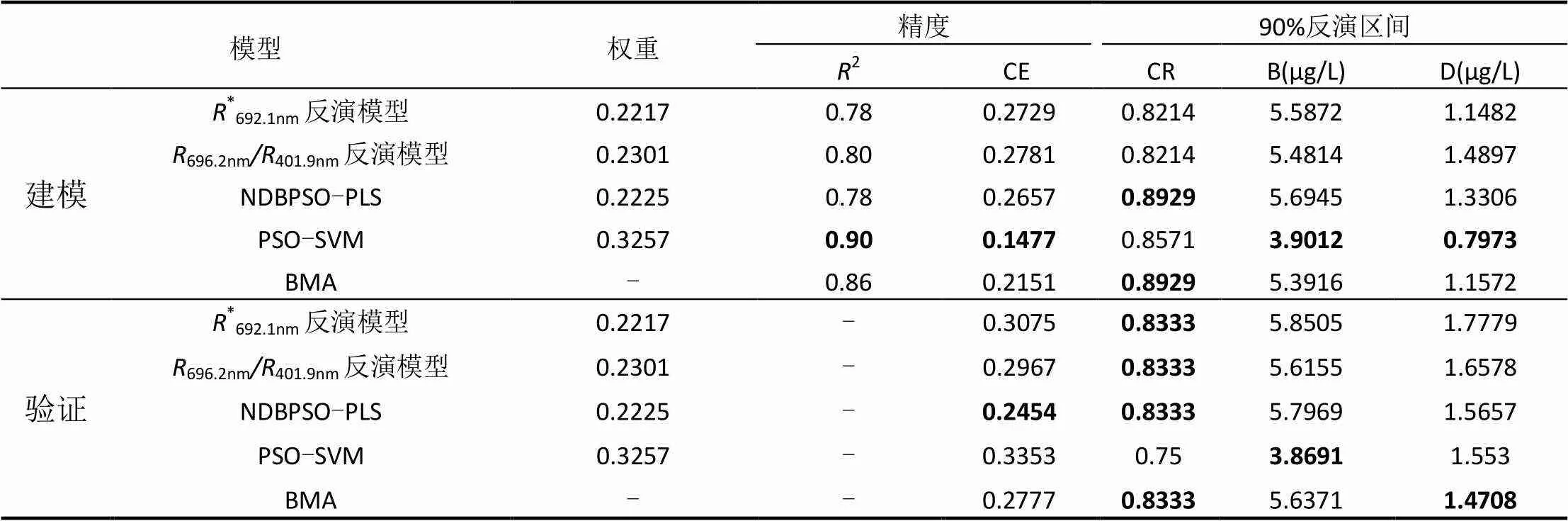
表6 叶绿素浓度BMA集合模型和各单一模型评价表

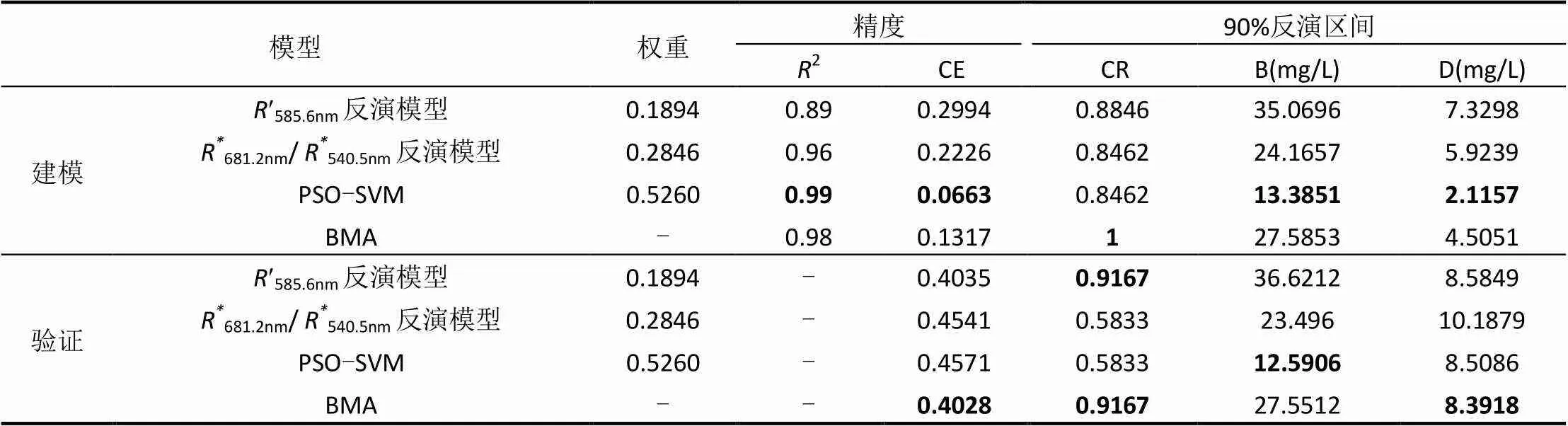
表7 总悬浮物浓度BMA集合模型和各单一模型评价表

表8 浊度BMA集合模型和各单一模型评价表

3.4 集合模型对比分析

由表3~表5中基于熵权法的EW-CM集合模型和基于集对分析的SPA-CM集合模型反演三种水质参数的精度评价结果对比分析可知,3种水质参数EW-CM和SPA-CM集合模型综合了各模型信息,同时具有较高的建模和验证精度.2种确定性集合模型中,SPA-CM集合模型建模2、建模综合误差、验证综合误差以及模型综合误差整体上要优于EW-CM集合模型, SPA-CM集合模型反演3种水质参数精度高于EW-CM集合模型.

结合表6~表8,从建模2来看,3种水质参数BMA集合模型整体上高于SPA-CM和EW-CM集合模型;从建模综合误差来看,叶绿素a浓度和总悬浮物浓度BMA集合模型要低于SPA-CM和EW-CM集合模型,浊度BMA集合模型和SPA-CM和EW-CM集合模型相当;从验证综合误差来看,3种水质参数BMA集合模型整体上要高于SPA-CM集合模型,和EW-CM集合模型相当.综上所述,BMA集合模型建模精度整体上优于SPA-CM和EW-CM集合模型,验证精度稍低于SPA-CM集合模型,和EW-CM集合模型相当,且差异较小.

BMA概率性集合模型相较于SPA-CM和EW-CM确定性集合模型的优势主要在于给定各模型权重构建集合模型的同时,可以给出集合模型和各模型反演水质参数的不确定性区间,利用区间覆盖率、平均带宽和平均偏移幅度来衡量各模型反演水质参数的不确定性.

3.5 讨论

集合建模可以综合各模型信息,提高模型稳定性,但集合模型的时空移植性需要进一步验证.后续将基于具有一定物理机理的内陆水体半经验/半分析模型进行集合建模,利用不同研究区和不同时序数据研究集合模型的时空移植性.

4 结论

4.1 3种水质参数不同反演模型建模和验证精度往往存在较大差异,两者难以一致,只利用单一模型进行水质参数反演充满了不确定性.

4.2 确定性集合模型中,3种水质参数SPA-CM和EW-CM集合模型建模和验证精度最大程度接近或一定程度高于单一最优模型,2种确定性集合模型同时具有较高的建模和验证精度,其中3种水质参数SPA-CM集合模型反演精度整体上优于EW-CM集合模型.

4.3 BMA概率性集合模型中,3种水质参数BMA集合模型建模精度和验证都最大程度接近或一定程度上高于单一最优模型,同时BMA方法可以给出集合模型和各模型反演水质参数的不确定性区间,3种水质参数BMA集合建模可一定程度提高区间覆盖率,降低平均偏移幅度,集合模型较单一模型具有更高的稳定性.

4.4 3种水质参数概率性BMA集合模型建模精度整体上要优于SPA-CM和EW-CM集合模型,验证精度稍低于SPA-CM集合模型,和EW-CM集合模型相当.

4.5 确定性和概率性集合模型可以综合各模型信息,使集合模型同时具有较高的建模和验证精度,降低单一模型反演水质参数的不确定性,并在一定程度上提高模型精度.

[1] 黄昌春,李云梅,徐良将,等.内陆水体叶绿素反演模型普适性及其影响因素研究 [J]. 环境科学, 2013,34(2):525-531.

[2] 冯 奇,程学军,沈 欣,等.利用 Landsat 8OLI 进行汉江下游水体浊度反演[J]. 武汉大学学报:信息科学版, 2017,(5):643- 647.

[3] Tian L Q, Chen X L, Li W B, et al. Retrieval of total suspended matter concentration from Gaofen-1Wide Field Imager (WFI) multispectral imagery with the assistance of Terra MODIS in turbid water–case in Deep Bay [J]. International Journal of Remote Sensing, 2016,37(14):3400-3413.

[4] Tian H, Cao C, Xu M, et al. Estimation of chlorophyll-a concentration in coastal waters with HJ-1A HSI data using a three-band bio-optical model and validation [J]. International Journal of Remote Sensing, 2014,35(16):5984-6003.

[5] 包 颖,田庆久,陈 旻,等.基于GOCI影像分类的太湖水体叶绿素a浓度日变化分析 [J]. 光谱学与光谱分析, 2016,36(8): 2562-2567.

[6] Ryan K, Ali K. Application of a partial least-squares regression model to retrieve chlorophyll-a [J]. Ocean Science Journal, 2016,51(2):209-221.

[7] 旷 达,韩秀珍,刘 翔,等.基于环境一号卫星的太湖叶绿素a浓度提取 [J]. 中国环境科学, 2010,30(9):1268-1273.

[8] Sun D Y, Li Y M, Wang Q. A unified model for remotely estimating chlorophyll a in Lake Taihu, China, based on SVM and in situ, hyperspectral data [J]. Geoscience & Remote Sensing IEEE Transactions on, 2009,47(8):2957-2965.

[9] 朱云芳,朱 利,李家国,等.基于GF-1WFV影像和BP神经网络的太湖叶绿素a反演 [J]. 环境科学学报, 2017,37(1):130-137.

[10] 袁 喆,严登华,杨志勇,等.集合建模在径流模拟和预测中的应用 [J]. 水利学报, 2014,45(3):351-359.

[11] 张凤太,苏维词,周继霞.基于熵权灰色关联分析的城市生态安全评价 [J]. 生态学杂志, 2008,27(7):1249-1254.

[12] 王文圣,李跃清,金菊良.基于集对原理的水文相关分析 [J]. 四川大学学报:工程科学版, 2009,41(2):1-5.

[13] 金菊良,魏一鸣,丁 晶.用基于加速遗传算法的组合预测模型预测海洋冰情 [J]. 系统管理学报, 2003,12(4):367-370.

[14] 吴静敏,左洪福,陈 勇.基于免疫粒子群算法的组合预测方法 [J]. 系统管理学报, 2006,15(3):229-233.

[15] 张 青.基于神经网络最优组合预测方法的应用研究 [J]. 系统工程理论与实践, 2001,21(9):90-93.

[16] 李 渊,李云梅,吕 恒,等.基于数据同化的太湖叶绿素多模型协同反演 [J]. 环境科学, 2014,35(9):3389-3396.

[17] 董磊华,熊立华,万 民.基于贝叶斯模型加权平均方法的水文模型不确定性分析 [J]. 水利学报, 2011,42(9):1065-1074.

[18] 王 斌,张洪波,辛 琛,等.基于贝叶斯模型加权平均法的径流序列高频分量预测研究 [J]. 水力发电学报, 2016,35(5):75-83.

[19] Raftery A E, Gneiting T, Balabdaoui F, et al. Using Bayesian model averaging to calibrate forecast ensembles [J]. Monthly Weather Review, 2005,113(5):1155-1174.

[20] Mueller, J.L., Fargion, G.S., Mcclain, C.R., et al. Ocean optics protocols for satellite ocean color sensor validation, Revision 4, Volume III: radiometric measurements and data analysis protocols [R].Greenbet, Maryland: NASA Goddard Space Flight Center, 2003.

[21] 唐军武,田国良,汪小勇,等.水体光谱测量与分析I:水面以上测量法 [J]. 遥感学报, 2004,8(1):37-44.

[22] GB11901-89 水质悬浮物的测定重量法 [S].

[23] Giorgio D, Gitelson A A, Rundquist D C. Towards a unified approach for remote estimation of chlorophyll-a in both terrestrial vegetation and turbid productive waters [J]. Geophysical Research Letters, 2003,30(18):159-171.

[24] Le C F, Li Y M, Yong Z, et al. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lakes: the case of Taihu Lake, China [J]. Remote Sensing of Environment, 2009, 113(6):1175-1182.

[25] 黎 夏.悬浮泥沙遥感定量的统一模式及其在珠江口中的应用 [J]. 遥感学报, 1992,7(2):106-114.

[26] 米 晨,汤秀芬,魏凤兰.基于Haar小波变换的图像分解与重构 [J]. 实验室研究与探索, 2003,22(2):78-81.

[27] 曹 引,冶运涛,赵红莉,等.基于离散粒子群和偏最小二乘的湖库型水源地水体悬浮物浓度和浊度遥感反演方法 [J]. 水力发电学报, 2015,34(11):77-87.

[28] Bazi Y, Melgani F. Semi-supervised PSO-SVM regression for biophysical parameter estimation [J]. IEEE Transactions on Geoscience and Remote Sensing, 2007,45(6):1887-1895.

Ensemble modeling methods for remote sensing retrieval of water quality parameters in inland water.

CAO Yin1,2, YE Yun-tao2*, ZHAO Hong-li2, JIANG Yun-zhong2, WANG Hao1,2, WANG Jun-feng1

(1.State Environmental Protection Engineering Center for Pollution Control in Textile Industry, College of Environmental Science and Engineering, Donghua University, Shanghai 201620, China；2.State Key Laboratory of Smimulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing 100038, China)., 2017,37(10)：3940~3951

Based on the measured hyperspectral data and concentration of chlorophyll a, total suspended matter (TSM) and turbidity obtained during June 11 to 13, 2015 in Weishan Lake, empirical models and PSO-SVM model were established to retrieve the three water quality parameters. Meanwhile, the performance of those models was evaluated to determine the models applied to ensemble modeling. The ensemble models containing EW-CM, SPA-CM and BMA were established to retrieve the three water quality parameters by using deterministic ensemble method and probabilistic ensemble method. The deterministic and probabilistic ensemble method was based on the entropy weight method along with pair analysis method and Bayesian averaging method, respectively. Bayesian averaging method was employed to obtain the retrieval uncertainty range of the three water quality parameters by using the single model and the BMA ensemble model, and the retrieval uncertainty range of these models was compared. These results demonstrated that (1) the accuracy of SPA-CM model was better than that of EW-CM model in deterministic ensemble models; (2) the modeling accuracy of BMA probabilistic ensemble model was better than that of SPA-CM and EW-CM model; the verification accuracy of BMA probabilistic ensemble model was similar with that of EW-CM model but slightly lower than that of the SPA-CM model; (3) Probabilistic ensemble modeling could obtain the retrieval uncertainty range of water quality parameters by using the ensemble model and the single model; (4) The deterministic and probabilistic ensemble model associated with the single model information showed a higher modeling and verification accuracy, which could be used to reduce the uncertainty of water quality parameters retrieval compared with single model and promote the retrieval accuracy of water quality parameters in a manner.

inland water；remote sensing of water quality；ensemble modeling；Weishan Lake；chlorophyll a；total suspended matter；turbidity

X832

A

1000-6923(2017)10-3940-12

曹 引(1991-),男,安徽滁州人,东华大学博士研究生,主要从事流域水资源遥感及水循环模型数据同化研究.发表论文10余篇.

2017-03-23

国家自然科学基金资助项目(51309254);国家重点研发计划资助项目(2017YFC0405801,2017YFC0405804);中国水利水电科学研究院科研专项“十三五”重点科研项目(WR0145B272016);中国水利水电科学研究院流域水循环模拟与调控国家重点实验室开放研究基金资助项目(IWHR-SKL-201517)

* 责任作者, 高级工程师, yeyuntao@iwhr.com