层次分析法的SAS/IML模块实现*

南通大学公共卫生学院流行病与卫生统计系(226019)

华天齐 沈 欢 李 洲 魏 源 高月霞 吴传莉 肖 静△

国家自然科学基金项目(71603137)；南通市科技局资助(MS22016039)；江苏省大学生创新训练计划项目(201710304076Y)

△通信作者：肖静，E-mail：jxiaoyz@163.com

层次分析法的SAS/IML模块实现*

南通大学公共卫生学院流行病与卫生统计系(226019)

华天齐 沈 欢 李 洲 魏 源 高月霞 吴传莉 肖 静△

目的基于SAS软件Data步实现层次分析法过于繁琐,本研究使用SAS/IML模块实现,以提高分析效率。方法SAS/IML模块编写程序实现层级分析法,计算各指标权重及其一致性检验,并与Data步实现层次分析法的分析结果进行比较。结果SAS/IML模块实现层次分析法,操作时仅需输入判断矩阵,调用模块即可得出结果,大大提高了分析速度,分析结果与使用Data步分析结果完全一致。结论SAS/IML模块实现层次分析法可以极大简化分析程序,程序的连贯性和整体性均更好。

层次分析法 SAS/IML

层次分析法(analytic hierarchy process,AHP)是由美国运筹学家Saaty于20世纪70年代提出的,应用网络系统理论和多目标综合评价方法的一种层次权重决策分析方法[1]。层次分析法将与决策有关的元素分解成目标、准则、方案等层次,在此基础上进行定性和定量分析。层次分析法目前在医药卫生领域应用广泛[2-3],SAS Data步实现层次分析法程序较为繁琐,本文旨在使用SAS/IML模块简化程序,提高分析效率，同时便于使用者操作。

基本原理

层次分析法的基本思想是将待解决的问题分层结构化,使一个复杂的问题转化为多层次多要素的结构,从而建立一个综合评价模型。把复杂的问题分解为若干组成要素,又将这些要素按支配关系分组形成递进层次结构,通过两两比较的方式确定同一层次和同一支配关系下各要素的相对重要性,构造判断矩阵,确定各要素对于其支配层的权重,最终确定最低层各要素的重要性,即确定最低层要素对于最高层(目标层)的权重。

实例分析和SAS程序实现

采用南通市餐饮服务食品安全监管量化分级评价指标权重体系构建的数据,通过层次分析法,确定各二级指标(最低层)的权重分值,应用于餐饮服务食品安全监管动态评价。

1.建立评价指标的层次结构

目标层:食品安全监管评价指标体系，分为:第一层9个一级指标,第二层30个二级指标,如一级指标环境卫生的4个二级指标,见图1。

图1 餐饮服务食品安全监管评价指标体系部分层次结构图

2.建立两两比较判断矩阵

以第一层次为例,9个一级指标的相对重要性,即第Ai指标相对于第Aj指标的重要性,由专家采用心理学9分位的比例尺度[4]打分完成,分值分别为:极重要9分,很重要7分,重要5分,略重要3分,同等重要1分,略次要1/3,次要1/5,很次要1/7和极次要1/9,且分值8,6,4,2,1/2,1/4,1/6,1/8为其中两个评价分值的中间评价值,多位专家的打分值求平均后,构造判断矩阵[5](表1),表中各数值为第i行指标相对于第j列指标的重要性的平均分值。同理,构造各一级指标下二级指标的判断矩阵,以一级指标环境卫生(A5)的4个二级指标为例构建的判断矩阵T5(表2)。

表1 9个一级指标的判断矩阵

表2 一级指标环境卫生(A5)的4个二级指标的判断矩阵

3.计算权重向量

层次分析法计算权重向量有和法、根法、特征根法等。这里我们采用根法,计算方法如下:

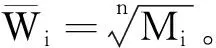
4.一致性检验

一致性指标CI=(λmax-n)/(n-1),一致性比率CR=CI/RI。RI为平均随机一致性指标,不同阶数的矩阵其值不同。当CR<0.1时,可认为判断矩阵有令人满意的一致性[6],计算得出的权重符合逻辑。

5.综合评价

将二级指标权重乘以对应一级指标权重,得到二级指标相对于总体的权重。

6.SAS程序实现

(1) 计算指标权重系数及一致性检验

proc iml;

start ahpmatrix(p);/*定义模块开始*/

p=p;

geom=J(nrow(p),1,1);/*初始化列向量*/

do i=1 to nrow(p);/*do循环计算行内乘积*/

geom=geom#p[,i];

end;

geom_mean=geom##(1/nrow(p));/*计算行内乘积的n次方根*/

geomsum=geom_mean[+,];/* 计算行内乘积n次方根和*/

weight=geom_mean/geomsum;

lambda=p*weight/weight;

lambdamax=lambda[+,]/nrow(p);

ci=(lambdamax -nrow(weight))/(nrow(weight) -1);

if nrow(p) <=2 then ri=0;/*定义RI值*/

else if nrow(p)=3 then ri=0.58;

else if nrow(p)=4 then ri=0.90;

else if nrow(p)=5 then ri=1.12;

else if nrow(p)=6 then ri=1.24;

else if nrow(p)=7 then ri=1.32;

else if nrow(p)=8 then ri=1.41;

else if nrow(p)=9 then ri=1.45;

else if nrow(p)=10 then ri=1.49;

else if nrow(p)=11 then ri=1.51;

else if nrow(p)=12 then ri=1.48;

else if nrow(p)=13 then ri=1.56;

else if nrow(p)=14 then ri=1.57;

else if nrow(p)=15 then ri=1.59;

if ri=0 then cr =.;

else cr=ci/ri;

a1=p||weight||lambda;/* 创建输出矩阵*/

a2=lambdamax||ci||ri||cr;

a3=a2//J(nrow(p)-1,4,.);

a5=a1||a3;

print a5;

return(weight);

finish ahpmatrix;/*定义模块结束*/

T={1 1.500 1.173 1.172 1.000 1.050 0.934 0.996 0.946,

0.667 1 1.182 0.964 0.881 0.643 0.826 0.855 0.635,

0.853 0.846 1 1.069 1.947 1.674 0.695 0.752 0.885,

0.853 1.037 0.936 1 1.485 1.678 1.776 1.119 1.318,

1.000 1.135 0.514 0.673 1 0.805 0.900 0.881 0.869,

0.953 1.555 0.597 0.596 1.242 1 1.439 1.846 1.271,

1.070 1.210 1.438 0.563 1.111 0.695 1 1.258 1.639,

1.004 1.170 1.329 0.894 1.134 0.542 0.795 1 1.071,

1.057 1.574 1.130 0.759 1.151 0.787 0.610 0.934 1};

w1=ahpmatrix(T);/*调用模块*/

A5={1 2.475 1.664 2.978,

0.404 1 1.425 2.656,

0.601 0.702 1 2.974,

0.336 0.377 0.336 1};

w2=ahpmatrix(A5);

(2) 计算环境卫生A5的4个二级指标的加权权重

将一级指标环境卫生A5的权重值乘以该指标下二级指标的权重值,得到4个二级指标占总体的权重值。同理可计算得到30个二级指标占总体的权重值。

tw=w1[5]#w2;/*计算环境卫生A5的4个二级指标占总体权重*/

print tw;

quit;

(3)分析结果

我们将SAS/IML模块分析结果与SAS/Data步实现层次分析法的分析结果进行比较,发现两种方法的分析结果完全一致,一级、二级指标及综合的权重值完全相同,见表3和表4。两种方法的一致性检验结果也完全一致,CR值均<0.1,说明9个一级指标的一致性(CI=0.034,CR=0.024)(表3)和环境卫生的4个二级指标的一致性(CI=0.035,CR=0.039)(表4)均较好,所计算出的权重符合逻辑。但IML模块分析程序比原先的Data步实现程序大大简化了,运行速度提高了25%。

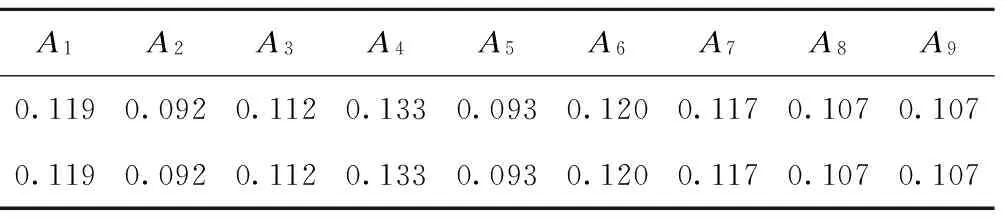
表3 9个一级指标的权重值

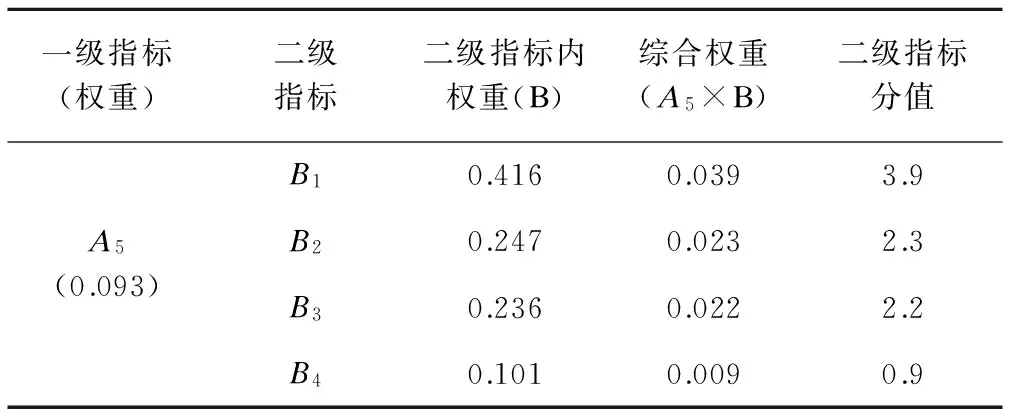
表4 环境卫生A5的4个二级指标内权重及综合权重

讨 论

层次分析法的实现涉及到矩阵的运算,SAS软件本身集成了IML模块专用于计算矩阵,因此采用IML模块可以简化程序,提高分析效率。本研究采用IML模块语言编程实现了计算各层次的权重及一致性检验的层次分析法,只需在程序模块中输入对应矩阵,调用该模块即可得到归一化权重系数、一致性检验结果和最终层次的最低层各指标占总体的权重值。而以往的研究[7]通过Data步在SAS中实现层次分析法的应用,每实现一次需编写并执行一次Data步,在层次较为复杂,需计算的矩阵数量较多的情况下,程序会变得冗长,效率低下,多次操作易错且不易纠错。本研究由于篇幅所限,实例分析中仅计算了9个一级指标和其中一个一级指标环境卫生的4个二级指标的权重,也就是仅涉及了2个矩阵的运算,IML模块实现程序的运行时间已比Data步程序实现分析的时间节省了25%,如果按照相同的方法计算出30个二级指标占总体的权重,涉及到10个矩阵,运算速度将进一步提高40%。随着层次结构的复杂,矩阵数量的增加,计算速度的优势尤为突显。

层次分析法的应用越来越普遍,本研究优化改进后的程序简单、可读性高,且只需调用模块,应用起来比较方便,有很强的实际应用价值。

[1] Saaty TL.How to make a decision:The analytic hierarchy process.Interfaces,1994,48(1):9-26.

[2] 王晓洁.京津冀医疗卫生服务均等化量化研究:基于AHP方法的分析.中国卫生经济,2015,34(10):48-50.

[3] 杨练,张雪莉,景琳,等.基于网络层次分析法的乡村医生政府补助性收入策略指标体系研究.中国全科医学,2016,19(16):1943-1950.

[4] Saaty TL,Forman EH.The Hierarchon:A Dictionary of Hierarchies.RWS Publications,1996.

[5] 王孝宁,何苗,何钦成.层次分析法判断矩阵的构成方法及比较.中国卫生统计,2002,19(2):111-113.

[6] 黄宝宏.层次分析法在评价应用中的统计学审视.中国卫生统计,2008,25(2):201-203.

[7] 王喜文,陈清.运用SAS程序实现层次分析法的综合评价.数理医药学杂志,2010,23(2):132-135.

(责任编辑：刘 壮)