考虑关节柔性的双连杆机械臂振动控制及实验研究

荣吉利，项 阳，辛鹏飞，杨永泰，项大林

(1.北京理工大学宇航学院力学系， 北京 100081；2.中科院泉州装备制造研究所，泉州 362200;3.北京宇航系统工程研究所，北京 100076)

考虑关节柔性的双连杆机械臂振动控制及实验研究

荣吉利1，项 阳1，辛鹏飞1，杨永泰2，项大林3

(1.北京理工大学宇航学院力学系， 北京 100081；2.中科院泉州装备制造研究所，泉州 362200;3.北京宇航系统工程研究所，北京 100076)

为了研究含有柔性关节的双连杆柔性机械臂的振动控制问题，采用绝对坐标方法对臂杆和关节进行建模，得到了刚柔耦合的双连杆机械臂动力学模型；对比研究了PD和LQR控制方法对柔性机械臂主动控制效果，针对柔性机械臂的实际工程需求，提出了一种LQR-PD联合控制策略，设计了相应的控制器并进行了仿真控制研究，同时结合搭建的双连杆柔性机械臂地面模拟平台进行了模拟实验。研究结果表明，该控制策略不仅能实现关节轨迹的精确跟踪，而且能有效抑制臂杆末端的残余振动，具有重要的工程价值和良好的应用前景。

多体系统动力学；双连杆柔性机械臂；振动控制；轨迹跟踪；地面仿真平台

0 引 言

随着空间技术的不断发展，空间机械臂作为在轨支持、服务的一项关键性技术，在航天器上得到了广泛的应用[1]。为了提高操作的机动性和灵活性，空间机械臂一般具有轻质、大跨度的特点，这注定了空间机械臂是一种强耦合、高度非线性的复杂柔性多体系统。关节柔性和臂杆柔性的客观存在是引起空间机械臂弹性振动的根本原因。这不仅会导致控制精度降低，还会引发系统共振，使结构过早产生疲劳破坏，影响结构的使用寿命。因此有效提高空间机械臂定位精度的同时降低系统的弹性振动是亟待解决的重要问题

在空间机械臂的动力学建模方面，刘志全等[2]指出空间柔性机械臂多体动力学模型和关节动力学模型的准确建立，有利于设计控制系统，从而提高机械臂的定位精度，加速臂杆末端的振动衰减。大多数学者[3-4]采用假设模态法进行建模。假设模态法把柔性杆的变形表示为一系列模态函数的线性组合，需考虑系统特征值问题，但只能处理形状简单、约束条件易求的系统，且只能处理臂杆的小变形问题。绝对坐标方法[5]能够精确的描述柔性体的大变形、大转动的问题，同时具有常数质量矩阵、不存在科氏力、离心力项等优点。荣吉利等[6]采用该方法深入研究了柔性机械臂的动力学建模问题。

在空间机械臂的振动控制方面，目前应用较为广泛的主动控制方法主要有PID控制、最优控制、自适应控制、智能控制等[7]。基于不同的控制策略，国内外学者在空间机械臂的振动控制问题都做出了努力。传统PID控制很难直接应用到柔性机械臂这样的复杂系统中，不少学者对其进行了改进并取得了较好的研究成果。Talebi 等[8]采用基于神经网络的PD控制策略对柔性机械臂的控制问题进行了研究。刘志全等[9]采用PID结合关节力矩反馈控制方案对对接任务中的关节力矩控制问题进行了研究。邓子辰等[10]在空间机械臂非线性动力学方程的基础上，运用线性二次型最优控制方法，对柔性机械臂的振动控制问题进行了研究，其动力学模型并未考虑关节柔性，且忽略了臂杆的轴向变形。Wu等[11]提出了一种用于单连杆柔性机械臂末端位置控制的模型参考自适应算法，但自适应控制算法的有效实施依赖于控制过程中对模型未知参数的准确估计和辨识，这无疑增加了控制结构的复杂性，因此导致控制器的实时性降低。Zmeu等[12]基于神经网络算法对单连杆柔性机械臂的线性模型进行了预测控制，证明该控制策略可以有效地补偿模型的不确定性和脉冲干扰，但在持续激励条件下，神经网络权值的收敛性得不到保证，因此对于经历过多次的同一控制任务，在每次执行时，神经网络都需要重新进行冗余而繁琐的训练。杨飞飞等[13]等采用确定学习中基于模式的控制思想实现了空间机械臂基于模式的控制，但该模型中并未考虑臂杆柔性和关节柔性的耦合对于控制效果的影响。

针对上述问题，本文采用绝对坐标方法对考虑关节柔性的双连杆机械臂进行建模。对柔性空间机械臂主动控制中的PD控制与LQR最优控制进行了对比研究，针对柔性空间机械臂的实际工程需求，提出了一种LQR-PD联合控制策略，设计了相应的控制器，对两自由度双连杆机械臂进行了数值仿真和模拟实验，验证了该控制策略的有效性。

1 柔性机械臂动力学建模

1.1绝对坐标方法建模

自然坐标法[14]通常选取刚体上两个固定点的位置矢量和两个正交单位矢量作为广义坐标，称之为“两点两矢”的坐标形式，如图1所示，该刚体具有12个广义坐标：

(1)

其中，ri、rj分别为刚体上固定点i、j的位置矢量，u和v为刚体上固定的正交单位矢量。刚体上任意一点在全局坐标系下的位置矢量可表示为：

r=Cq

(2)

绝对节点坐标方法由Shabana等[5]提出，采用节点位移和位移梯度作为广义坐标来描述有限单元的运动和变形，适用于研究经历大范围运动的柔性多体变形问题。

图2为基于绝对节点坐标方法描述的全参数矩形梁单元模型，该单元具有24个广义坐标：

(3)

式中：ri、rj分别为固定点i、j的位置矢量，rβ,α=∂rβ/∂α(β=i,j;α=x,y,z)表示固定点的斜率矢量。单元上任意一点在全局坐标系下的位置矢量可表示为：

r=Sq

(4)

式中：S为形函数矩阵，具体形式可参见参考文献[5]。

1.2柔性机械臂关节建模

本文采用Spong等[15]提出的线性“转子-扭簧系统”模型，该模型通过将关节简化为扭簧，忽略关节内部传动装置动力传动关系，只考虑关节输出力矩与关节输出运动参数关系。简化模型如图3所示：

在电机转子和电机壳体上分别建立NCF坐标，分别用qm和qs表示，由qm和qs可以得到电机转子和关节壳体的转角θm和θs。电机、关节所受力矩为：

(5)

式中：τ为电机受到的驱动力矩，与电流大小有关；τm为电机受到的力矩；τs为关节受到的力矩；θs为柔性关节系统转动的角度，即电机与关节的相对转动角度；θm为电机实际转动角度；K表示扭转弹簧的非线性扭转刚度，一般通过实验手段测量获得关节扭矩和转角后对数据进行拟合修正，进而获得柔性关节的非线性扭矩-转角曲线。

1.3柔性机械臂状态方程

以单臂杆柔性空间机械臂为例，推导柔性空间机械臂的状态空间方程，建立相应的控制系统模型。图4为单连杆柔性空间机械臂的平面示意图，为了降低关节轨迹规划中臂杆末端振动以及加速规划结束后的残余振动，选取关节转角和末端弹性振动的角度作为控制变量：

(6)

式中：θ11为关节转角，θ12为臂杆末端弹性振动的角度。结合Lagrange方程，可以得到如下形式的动力学方程：

(7)

式中：M为系统广义质量矩阵，B为系统广义阻尼矩阵，K为系统广义刚度矩阵，Qf为系统广义外力矩阵。

(8)

相应的系数矩阵为：

(9)

其中，Ksl为柔性臂杆弯曲刚度系数；J11为电机等效转动惯量；B11为关节等效粘滞阻尼系数；J12为柔性臂杆等效转动惯量；B12为柔性臂杆等效粘滞阻尼系数；Ksl为电机转矩常数。

由于数值仿真与模拟实验设定的关节转速较低，臂杆的阻尼项对于系统的动力学特性影响较小，因此，为了简化起见，在双连杆柔性机械臂动力学建模过程中忽略了臂杆的阻尼项。

2 柔性机械臂振动控制策略

2.1PD控制策略

为实现关节对预定轨迹的精确跟踪，降低规划结束后关节转角的残余振动，设计了基于关节转角误差调节的PD控制器，控制律形式如下：

(10)

式中：θref为关节预定轨迹，θ为关节实际轨迹，kp为比例增益矩阵kp=diag(kp1,kp2)，kd为微分增益kd=diag(kd1,kd2)，矩阵中的控制参数通过多次试探仿真确定。本节采用PD控制策略来实现双连杆柔性机械臂关节轨迹跟踪控制，如图5所示。

2.2LQR最优控制策略

LQR最优控制问题是在线性系统的约束条件下，寻找一个控制输入，使得二次型性能指标函数取得极值[14]。

基于前文推导所得的柔性机械臂状态空间方程(8)，性能指标函数简化形式如下：

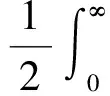
(11)

式中：Q为半正定的对称常数矩阵，R为正定的对称常数矩阵。

寻找最优输入量，即电机的控制电流为：

u*(t)=-R-1BTPx(t)=-Kfbx(t)

(12)

使得二次型性能指标函数(11)取得极小值。式(12)中Kfb为状态反馈增益矩阵，P为常数矩阵，且满足下列代数Riccati方程：

PA+ATP-PBR-1BTP+Q=0

(13)

式中：矩阵A、B、C的具体形式如式(9)所示。

加权矩阵Q和R的取值具有一定的相对性，本文为了便于最优控制问题的求解，将矩阵R设为单位矩阵，并结合柔性机械臂实际工程经验采用极点最优配置[16]的方法调整确定加权矩阵Q中元素值。LQR最优控制下的双连杆柔性机械臂闭环控制系统如图6所示。

2.3LQR-PD联合控制策略

PD控制器通过对关节转角误差的调节，虽然实现了关节对预定轨迹的精确跟踪，但是在过程的启动、结束或大幅增减设定时，短时间内系统输出会有很大偏差，因此传统PD控制策略很难直接应用于实物仿真控制；LQR控制器通过对系统输入能量的控制，使其控制信号更为平滑，从而避免了控制量的高频抖动给系统带来的不稳定的问题，但是由于LQR控制器初始输入信号较大，关节轨迹相对于预定轨迹而言存在较大控制误差，无法满足精确跟踪的控制要求。

因此，针对柔性机械臂实际应用过程中对于位置跟踪和弹性振动抑制这两方面要求，本文提出一种LQR-PD的联合控制策略。一方面通过引入PD控制实现了关节轨迹的精确跟踪，另一方面通过引入LQR控制器对系统的输入能量进行控制，解决了PD控制过程中的超调问题，有效地抑制了臂杆末端的弹性振动。LQR-PD联合控制下的双连杆柔性机械臂闭环控制系统如图7所示。

3 仿真校验

采用图8所示的双连杆柔性机械臂对所提出的控制策略进行验证，其中，臂杆1长0.202 m，宽7.62×10-2m，厚度为1.27×10-3m，杨氏模量为80 Gpa，密度为1.8×103kg/m3，泊松比为0.3；臂杆2宽3.81×10-2m，其余材料参数与臂杆1保持一致。关节壳体内径为0.05 m，外径为0.1 m，高度为0.2 m，密度为1.8×103kg/m3，泊松比为0.3；关节电机内径为0 m，外径为0.05 m，高度为0.1 m，其余材料参数与关节壳体保持一致。机械臂所有柔性关节均只能绕其转轴转动。

(14)

规划时间为3 s，仿真时间设置为5 s。

PD控制参数和LQR加权矩阵Q选择如下：

(15)

图9为不同控制状态下关节转角仿真轨迹与预定轨迹的对比。图10为臂杆末端弹性振动情况。关节端无控制状态下，在轨迹规划阶段，关节轨迹相比于预定轨迹而言存在一定的跟踪误差，且在轨迹规划结束后，关节转角存在一定幅度大小的残余振动，这会引起臂杆末端残余振动，导致控制精度下降。通过引入PD控制器可以实现关节轨迹对预定轨迹的精确跟踪，但是无法从根本上对臂杆末端的残余振动进行有效地抑制。通过引入LQR控制器对系统输入能量的控制，降低了运动阶段的弹性振动同时，有效地抑制了臂杆末端残余振动，但在运动阶段关节实际轨迹对预定轨迹的跟踪误差较大。

由于单独使用一种控制算法不能满足实际工程需求，因此，通过设计LQR-PD控制器，对双连杆机械臂进行仿真控制。图11～12为联合控制策略控制下，关节转角仿真轨迹与预定轨迹对比以及柔性臂杆末端的弹性振动变化情况。从图11可以看出，在轨迹规划段，联合控制策略能够实现关节对预定轨迹的精确跟踪，轨迹规划结束后，末端残余振动能够得到有效地抑制。在整个运动过程中，通过引入联合控制策略，臂杆末端弹性振动有了明显的减弱，其中臂杆1末端弹性振动幅值由1.86°减弱至0.22°，减弱了88.3%；臂杆2末端弹性振动幅值由0.98°减弱至0.14°，减弱了85.7%。这说明本文提出的联合控制策略在实现关节对于预定轨迹精确跟踪的同时，有效地抑制了臂杆末端的弹性振动。

4 实验研究

4.1柔性机械臂振动控制实验平台

为验证上文所提联合控制策略的有效性，利用两自由度柔性双连杆机械臂装置，搭建振动控制平台如图13所示。该控制平台主要由操控计算机、数据采集卡、功率放大器以及两自由度柔性双连杆机械臂组成。操控计算机上安装有QuaRC实时控制软件，该软件能够与Matlab/Simulink兼容，将系统中数据采集硬件端口做成相应的Simulink模块，通过Simulink直接对硬件端口进行读、写操作，将设计的控制器与相应的系统硬件端口模块连接，编译下传到QuaRC控制软件中，就能对系统进行实时仿真控制。

4.2实验结果

图14为LQR-PD联合控制下的双连杆机械臂的关节实际轨迹与预定轨迹对比，可以看出，两个关节均能按照预定轨迹到达指定角度，运动段结束无明显残余振动。图15为关节1和关节2对预定轨迹的跟踪误差，关节转角跟踪误差为10-3量级，满足工程需求。图16为臂杆1和臂杆2末端弹性振动实验结果与仿真结果的对比，考虑实验误差存在的情况下，模拟实验与数值仿真的结果基本吻合。 进一步验证了本文所提联合控制策略的有效性。

5 结 论

本文针对双连杆机械臂轨迹跟踪及振动控制问题进行了数值仿真与模拟实验，获得以下结论：

1)采用绝对坐标方法建立了比较完备的包含关节和臂杆柔性的刚柔耦合动力学模型，该模型能够精确地描述机械臂系统大变形、大转动问题；

2)通过对比研究PD控制策略和LQR控制策略的优劣性，提出一种LQR-PD联合控制策略，仿真控制结果表明联合控制策略在实现柔性机械臂关节转角精确跟踪的同时降低了臂杆末端的弹性振动；

3)设计相应的控制器，通过搭建地面实验控制平台进行实物控制实验，实验结果与仿真结果基本吻合，进一步验证了联合控制策略的有效性。

[1] 于登云, 孙京, 马兴瑞. 空间机械臂技术及发展建议[J]. 航天器工程, 2007, 16(4):1-8. [Yu Deng-yun, Sun Jing, Ma Xing-rui. Suggestion on development of Chinese space manipulator technology [J]. Spacecraft Engineering, 2007, 16(4): 1-8.]

[2] 刘志全, 危清清, 王耀兵. 载人航天器柔性机械臂的动力学建模方法[J]. 航天器工程, 2013, 22(5):34-41. [Liu Zhi-quan, Wei Qing-qing, Wang Yao-bing. Review of flexible manipulator dynamic modeling of manned spacecraft [J]. Spacecraft Engineering, 2013, 22(5):34-41.]

[3] 戈新生, 崔玮, 赵秋玲. 刚柔性耦合机械臂轨迹跟踪与振动抑制[J]. 工程力学, 2005, 22(6): 188-191. [Ge Xin-sheng, Cui Wei, Zhao Qiu-ling. Trajectory tracking control and vibration suppression of rigid flexible manipulators [J]. Engineering Mechanics, 2005, 22(6): 188-191.]

[4] 梁捷，陈力. 柔性空间机械臂末端运动及柔性振动的模糊自适应补偿控制[J]. 兵工学报, 2011, 32(1): 45-57. [Liang Jie, Chen Li. Fuzzy logic adaptive compensation control of end-effect motion and flexible vibration for space-based flexible manipulator [J]. Acta Armamentarii, 2011, 32(1): 45-57.]

[5] Shabana A A, Yakoub R Y. Three dimensional absolute nodal coordinate formulation for beam elementstheory [J]. Journal of Mechanical Design, 2001, 123(4):614-621.

[6] 荣吉利, 杨永泰, 李健,等. 空间机械臂建模方法与控制策略研究[J]. 宇航学报, 2012, 33(11):1564-1569. [Rong Ji-li, Yang Yong-tai, Li Jian, et al. Research on modeling and control scheme of space manipulator [J]. Journal of Astronautics, 2012, 33(11):1564-1569.]

[7] 张晓东, 贾庆轩, 孙汉旭,等. 空间机器人柔性关节轨迹控制研究[J]. 宇航学报, 2008, 29(6):1865-1870. [Zhang Xiao-dong, Jia Qing-xuan, Sun Han-xu，et al. The research of space robot flexible joint trajectory control [J]. Journal of Astronautics, 2008, 29(6):1865-1870.]

[8] Talebi H A, Patel R V, Asmer H. Neural network based dynamic modeling of flexible-link manipulators with application to the SSRMS [J]. Journal of Robotic Systems, 2000, 17(7):385-401.

[9] 刘志全, 危清清, 王耀兵. 空间机械臂关节精细动力学模型的建立及关节力矩控制[J]. 宇航学报, 2014, 35(6):663-668. [Liu Zhi-quan, Wei Qing-qing, Wang Yao-bing. Detailed joint dynamics modeling and joint torque control system of space manipulators [J]. Journal of Astronautics, 2014, 35(6):663-668.]

[10] 邓子辰, 钟万勰. 空间刚柔性机械臂振动的精细控制[J]. 力学季刊, 2000, 21(3):277-281. [Deng Zi-chen, Zhong Wan-xie. Precise control of vibration for rigid-flexible mechanical arm [J]. Chinese Quarterly of Mechanics, 2000, 21(3):277-281.]

[11] Wu S, Cetinkunt S. Model reference adaptive inverse control of a single link flexible robot [J]. Computers & Structures, 1993, 47(2):213-223.

[12] Zmeu K V, Shipitko E A, Perevozchilov A S. Linear neural model-based predictive controller design for flexible link robot [C]. IEEE International Symposium on Intelligent Control, Taipei, Sept 4, 2004.

[13] 杨飞飞, 王聪, 曾玮. 空间机械臂的确定性学习控制[J]. 宇航学报, 2015, 36(7):811-818. [Yang Fei-fei, Wang Cong, Zeng Wei. Learning from adaptive control of a class of space manipulator systems [J]. Journal of Astronautics, 2015, 36(7): 811-818.]

[14] García-Vallejo D, Mayo J, Escalona J L, Domínguez J. Three-dimensional formulation of rigid-flexible multibody systems with flexible beam elements [J]. Multibody System Dynamics, 2008, 20(1): 1-28.

[15] Spong M W. Modeling and control of elastic joint robots [J]. ASME Journal of Dynamic Systems, Measurement and Control, 1987, 109(6): 310-319.

[16] 倪茂林, 吴宏鑫. 具有完整性的最优控制系统设计[J]. 控制理论与应用, 1992(3):245-249. [Ni Mao-lin, Wu Hong-xin. The design of optimal control systems possessing integrity [J]. Control Theory and Applications, 1992(3):245-249.]

VibrationControlandExperimentResearchofTwo-LinkFlexibleManipulatorConsideringFlexibilityoftheJoint

RONG Ji-li1, XIANG Yang1, XIN Peng-fei1, YANG Yong-tai2, XIANG Da-lin3

(1. Department of Mechanics, School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China; 2. Quanzhou Institute of Equipment Manufacturing, Chinese Academy of Sciences, Quanzhou 362200, China;3. Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China)

In order to learn the vibration control of two-link flexible manipulator considering the flexibility of the joint, Absolute Coordinate Based (ACB) is utilized to model space manipulator links and joints to develop the dynamic equations of a rigid-flexible coupling two-link flexible manipulator system. The comparative study is carried on LQR and PD for active control of the flexible manipulator. Aiming at the practical engineering requirements of the flexible manipulator, a combined control strategy by LQR-PD is proposed. The controller is designed and applied to the simulation of the two-link flexible manipulator. Two-link flexible manipulator platform is set up and the control experiment is conducted. Results show that the proposed strategy is effective in tracking of the joint trajectory accurately and inhibiting the residual vibration of the end of the link, which means it has important practical significance and broad application prospect.

Dynamics of multi-body system; Two-link flexible manipulator; Vibration control; Trajectory tracking; Ground simulation platform

O313.7

A

1000-1328(2017)10- 1024- 08

10.3873/j.issn.1000-1328.2017.10.002

2017- 06- 05;

2017- 07- 17

CAST创新基金(CAST20100141107)

荣吉利(1964-)，男，博士，教授，主要从事振动控制理论与应用、水下爆炸理论与数值仿真、柔性多体系统动力学、可靠性理论与应用。

通信地址：北京市海淀区中关村南大街5号 北京理工大学宇航学院力学系(100081)

电话：(010)68912732

E-mail: rongjili@bit.edu.cn