振荡压路机压实机理再探讨

姜右良

江苏骏马压路机械有限公司，江苏 靖江 214501

振荡压路机压实机理再探讨

姜右良

江苏骏马压路机械有限公司，江苏 靖江 214501

导语：振荡压路机是近几年开始受到重视的一种多功能压实机械，2016年本刊曾刊出万汉驰撰写的一篇《振荡压路机深剖简析》，介绍了振荡作用到底是怎样的表现方式。那么振荡压路机是怎样作用于土壤颗粒的？土壤颗粒的受力状态是如何变化的？振荡压实的本质是什么？振荡压实和水平振动、轮胎压实的区别与联系是什么？这次就让我们一探究竟。

振荡压路机从诞生至今已有30多年的历史，振荡轮的结构和运动特征已被相关单位、科研人员研究的比较透彻和深入[1-2]，其压实机理可用一句话进行概括：在交变力矩的作用下，振荡轮以“揉搓”的方式作用于路面，使得土壤颗粒重新排列，进而提高路面密实度。大部分文献对振荡压实机理的解释止乎于此，而压实必然与被压实的土壤有关，仅通过分析振荡轮的运动特性并不足以表征振荡压实的本质，本文在现有研究成果的基础上，从振荡轮“宏观”运动和土壤颗粒的“微观”受力两个方面阐述了振荡压实的工作过程，对压实机理的本质做了更加深入的讨论与分析，即是文章标题“振荡压路机压实机理再探讨”中“再”字的由来。

关于振荡压路机振荡轮的结构设计、荡幅计算、实现方式等内容，江苏骏马压路机械有限公司技术人员曾在内部展开过激烈的讨论。笔者向万汉驰先生进行了虚心的请教，尤其是研读了万汉池先生的《振荡压路机深剖简析》一文，进一步加深了对振荡压路机“振荡作用到底是怎样的表现方式”这个问题的认识[3]，由此想到往复运动的振荡轮是怎样作用于土壤颗粒的、土壤颗粒的受力状态是如何变化的、振荡压实的本质是什么等一系列问题。无论何种压实方式（包括圆周振动、垂直振动、振荡及静碾压实等），最终要着眼于路面压实效果，因此从振荡轮与土壤颗粒间相互作用着手是研究振荡压实理论的切入点，以此切入分析可解释上述疑问，进一步阐述振荡压实机理，在讨论争辩中产生思想的火花，所谓“百家争鸣”才能够“百花齐放”，道理亦是如此。

言归正传，振荡压路机振荡作用对周边环境振动影响较小，尤其适用于桥梁、古建筑等对振动较敏感的场合，对于沥青面层的平整度和压实度具有较好效果，这些方面已然在实际应用中得到证实[4-5]，在未来道路施工中，振荡压路机的作用和地位必然呈上升趋势。对振荡轮结构特征、运动方式、压实机理等方面的认知不但是专业设计研究人员所应具备的专业素质，同时也可为施工方选型提供依据，所谓“知其然知其所以然”。本文在振荡压实三要素的前提下分析了振荡轮对土壤颗粒的运动响应，在振荡轮滚动工作状态下研究压实作用机理，研究结论对开发设计以及应用振荡压路机具有实际应用价值。

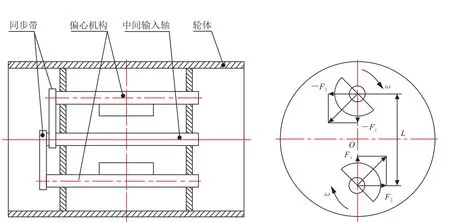
图1 振荡轮三轴结构

振荡压路机振荡理论

不少文献在阐述振荡轮结构及其运动原理时标题普遍称作“振荡压实原理”、“振荡压实机理”等[6-7]，而描述内容多半是振荡轮自身的运动特征，轮体与被压路面之间的相互作用以及土壤颗粒的运动特性甚少提及，严格来讲这一类称呼是不确切的；压实必然与被压实的介质有关，因此在描述振荡发生机构的原理性内容时标题中去掉“压实”两字，称作“振荡理论”或“振荡原理”更为贴切。

（1）振荡发生机构。

振荡运动是利用绕轮体轴芯的扭振力矩作用激励轮体，产生往复性的扭摆运动。振荡轮内部发生机构通常采用成本较低的三轴结构，如图1所示，中间输入轴为动力输入轴，2套相同的偏心机构绕轴芯对称安装，相位差为180°，在同步带的传动作用下2个偏心机构同步同向高速旋转，产生2组大小相等方向相反的离心力，绕轮体轴芯形成力偶矩，如图2所示。

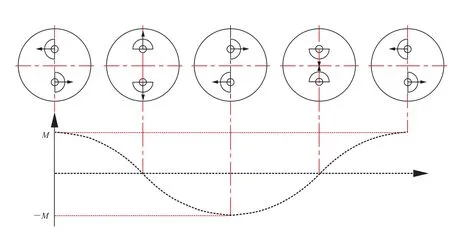
图2 偏心机构位置变化与交变力矩关系

当2个偏心机构的离心力方向与两者旋转中心连线相互垂直时，力偶矩达到最大值M（或－M）；当离心力方向与两者旋转中心连线相互平行时，力偶矩为零，偏心机构每旋转1周，力矩方向改变1次，匀速旋转过程中力矩按正（余）弦规律变化，交变力矩的作用迫使轮体绕轴芯产生往复性扭摆运动。需要注意的是：为清楚表达力矩大小和方向的变化情况，图2中的偏心机构旋转过程中轮体处于原地运动状态，即无滚动前进速度，而在压实工况下，偏心机构在高速绕自身轴芯以角速度ω“自转”的同时，轮体持续滚动碾压前进，偏心机构绕轮体轴芯产生角速度ω1的“公转”，如图3所示；力矩的作用中心绕轮体轴芯，与轮体滚动中心线重合，因此“公转”现象对力矩的影响只是相位的提前或滞后，对其大小和方向无实质性影响。

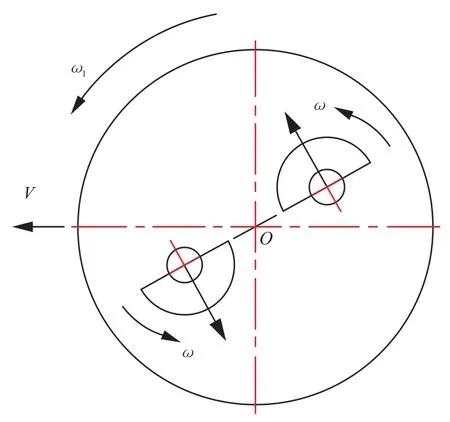
图3 振荡轮滚动工作示意

（2）名义荡幅的数学计算。

振荡轮作为整体运动的刚性体，交变力矩的作用迫使轮体绕其轴芯产生往复性扭摆运动，在轮体设计尺寸定型的条件下，扭摆运动的角度决定了轮体外圆质点的运动范围，即振荡轮荡幅幅值。关于振荡轮名义荡幅的推导与计算，文献[3]、[8]中做了详细透彻的介绍，设振荡轮扭摆角度为2θ（单位为rad，见图4），名义荡幅A0（mm）计算公式为如下。

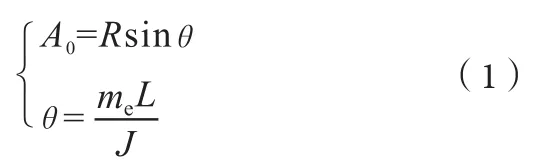
在实际运动中，θ值较小，式（1）可简化为

式中：R为振荡轮外圆半径（mm）；me为单个偏心机构的静偏心矩（kg·m）；L为两偏心机构“自转”中心间的距离（m）；J为振荡轮参与运动的刚形体绕轴芯的转动惯量（kg·m2）。

由式（2）可知，名义荡幅A0与轮体转动惯量J成反比，与轮体外圆半径R成正相关关系，与偏心机构的设计参数me、L两者的乘积存在正相关关系，设计人员可参照此关系并根据实际需要调整变量，得到满足要求的名义荡幅幅值。

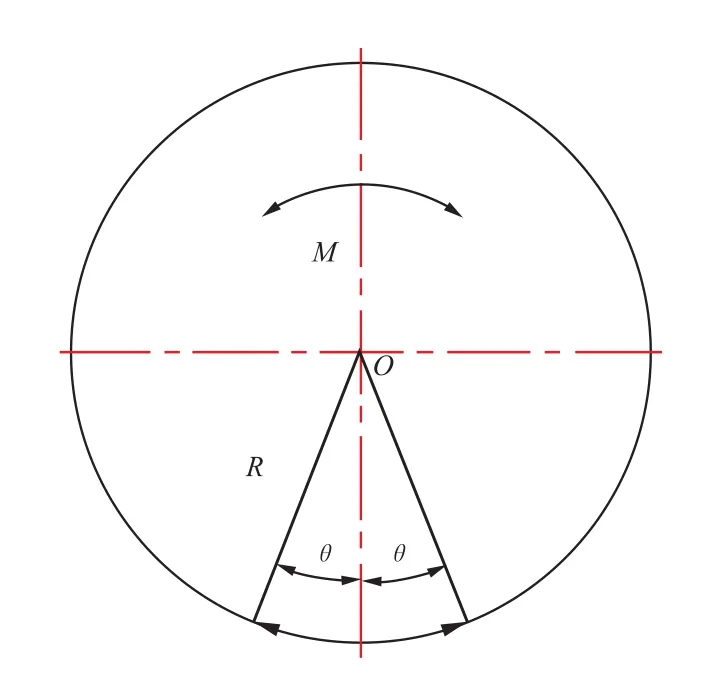
图4 振荡轮扭摆运动示意

关于名义幅值的讨论

（1）关于名义幅值的定义。

名义振幅与名义荡幅统称为名义幅值，《土方机械压路机和回填压实机术语和商业规格》（GB/T 7920.5—2003）中对振动压路机名义振幅的定义为：偏心矩乘1000除以振动部分质量；名义荡幅的定义暂无国家标准明确给出，其中缘由可能是行业内关于振荡压路机的研究尚不成熟，振荡结构形式多变，理论方面的复杂推导和计算仍存在争议，在未有统一公认的定论之前不可盲目定义。参照国标对名义振幅的描述，可以确定名义荡幅的定义是其计算公式的描述，若式（2）被业内认可并用于指导实际应用，其公式组成的描述就是名义荡幅的定义。在诸多书籍或期刊文献中名义幅值的定义被描述为“把压路机用支撑物支撑起来，压轮悬空时测得的幅值”，此描述与国标中的定义有着本质的区别。

国标中对名义幅值的定义描述为理论计算公式，进一步理解可发现其计算的前提是振动轮/振荡轮处于自身保守系统内，即轮体运动不受外界条件的任何约束，纯粹是自身激振发生机构引起轮体的运动[9]；众所周知，此条件在有引力的地球环境中是不存在的，因此才称其为名义振幅（也称理论振幅），如同牛顿第一定律，是理想条件下的理论值。压轮悬空只是解除了地面作用约束，车架减振器对轮体的约束依然存在，偏心旋转机构间的摩擦不可避免，通过仪器检测到的幅值受到多方面约束因素的影响，因此把悬空检测方法作为名义振幅的定义是欠妥当的，况且检测值和理论计算值的大小也不相等。不少文献在计算名义幅值时首先建立受约束的动力学模型，经方程推导得出较复杂的计算结论，最后再忽略约束简化公式，得到正确的推导结论，看似推导无误，实则自圆其说；建立受约束的数学模型这个前提就是错误的，名义幅值计算的前提是理想下的保守系统内，增加约束再忽略约束，似乎是为了计算而计算。悬空检测方法在实际生产中被广泛应用，其约束相对较少，检测值与名义幅值接近，因而在应用中可校对设计理论值的准确性，检测值因受约束条件限制，幅值比理论计算值略小。名义幅值的不可测量性决定了采用公式描述作为定义更加贴切。

（2）名义幅值与工作幅值的关系。

理论计算的名义幅值可指导结构设计，压路机工作压实过程中的幅值为工作幅值，工作幅值受到约束作用，与名义幅值的差距必然增大，差值的大小与被压实土壤的特性存在关系。对于振动压路机而言，振动轮以位移性冲击的方式作用于地面，由于地面的反弹作用，工作振幅高于名义振幅，随着地面密实度的增大，工作振幅与名义振幅的差值会增大，根据对试验检测结果的分析，一般情况下工作振幅A与名义振幅A0存在以下关系[10]。

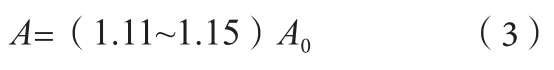
关于振荡压路机中工作荡幅和名义荡幅的比较，暂无试验数据表明其数学关系，但可通过分析确定其大小。振荡轮的扭摆运动特征决定了轮体在压实过程中与路面时刻保持接触，轮体作为压实的主动方揉搓土壤，路面对其往复扭摆运动起到阻碍作用，由此可知工作荡幅低于名义荡幅，在相同级配的环境里，随着土壤密实度的增加，土壤颗粒位移变小，轮体与路面的接触面积减小，工作荡幅与名义荡幅的差值会减小，与振动压路机振幅的变化规律相反，工作荡幅A与名义荡幅A0存在以下关系。

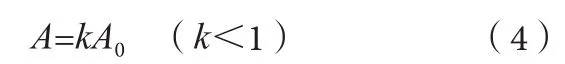
比例系数k值与土壤级配、路面密实度等因素有关，需经大量试验数据统计确定其取值范围。

振荡压实理论

（1）振荡压实的必要条件。

振荡压路机正常压实工作的必要条件包括工作质量、碾压速度和振荡运动，同时具备此三要素是振荡压实的前提，工作质量是机器本身的固有属性，碾压速度和振荡运动是机器的特有属性，三者对振荡影响至关重要。某些研究振荡压实数学模型的文献忽略碾压速度的作用，使得轮体约束与实际不符，分析数据存在较大偏差，如图5（b）、（d）所示，无碾压速度状态即原地起振，轮体两侧约束对称，普遍简化为水平受力，正常工作状态下被碾压过的路面与轮体接地点中心处相切，约束只在前进方向一侧，且接触面积只是原地起振的一半，轮体受力方向和大小均有差别。

针对上述分析可能存在的疑问是碾压路面铺层前后的高度差h较小，轮体对土壤作用的水平受力远大于竖直受力，简化为纯水平受力有何不可？如果只是研究振荡轮自身的运动特征完全可以忽略竖直受力，因为轮体运动的振源在其内部，外界约束作用对其运动趋势无实质性影响。当研究振荡压实对路面土壤的响应特性时，此简化过程忽略了工作质量（包括压路机上车质量和轮体自身质量）对压实的影响，工作质量反映到压路机外在表征是其一项重要技术参数，即静线压力。无工作质量状态下轮体与路面之间只是线接触，如图5（a）所示，无面接触无相互作用力，因此无压实效应，工作质量作为固有属性时刻存在并发挥作用，是振荡压实的必要条件。

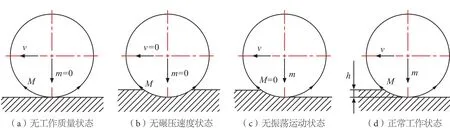
图5 压实三要素对振荡压实的影响

无碾压速度状态下的振荡压实见图5（b），轮体只是在原地绕轴芯往复运动，同样只是适用于振荡轮自身运动特征的研究，压实的对象是具有平面面积特征的路面，滚动前进是正常施工的前提，因此碾压速度也是振荡压实的必要条件。此外，振荡压实的本质是要发生振荡运动，否则“振荡压实”不能称之为“振荡”，图5（c）所示为无振荡运动状态，这是静碾压实，已不属于振荡压实的范畴。

工作质量、碾压速度和振荡运动作为振荡压实的必要条件都可进行量化设计与评估，3个参数之间匹配合理可有效提高压实效率和压实质量，具体匹配取值范围需对振荡压实做进一步研究和试验。

（2）振荡压实机理。

振荡发生机构的交变力矩作用使得轮体产生绕轴芯的往复扭摆运动，轮体与路面保持接触，无位移性冲击，依靠的完全是轮体与土壤颗粒间的相对滑动作用。轮体外圆面对土壤颗粒施加切线方向的作用力，迫使颗粒发生较大的动量变化（包括大小和方向），瞬间的大加速度可迅速破坏掉颗粒间摩擦阻力。根据土壤力学理论，当土壤的抗剪强度不足以抵抗某一面上的剪切力作用时，土壤将沿该剪切力方向产生急剧变形。物体间接触性质的切向作用力产生的原因是摩擦，振荡轮与土壤颗粒间的摩擦作用是振荡压实所利用的物理学理论；假若无相互摩擦作用，振荡轮的扭摆运动对颗粒位移毫无影响，出现图5（c）所示状态，振荡特征不复存在，成为静碾压实。高频运动的轮体反复作用在土壤铺层，颗粒受到往复的切向摩擦作用力，致使土壤材料沿剪切面破坏或滑移互相填充和楔紧而提高密实度，振荡压实机理阐述中所谓“揉搓”作用形象的描述由此而来。

克服土壤颗粒间的摩擦约束阻力需要振荡轮做功，消耗的是振荡轮的运动动能，能量的损耗必然削弱其运动状态，反馈到外在表征是工作荡幅幅值的降低，从能量的角度可验证式（4）的正确性。

振荡轮与土壤颗粒之间的最终作用是力的作用，在具备振荡压实三要素的前提下，土壤颗粒从接触轮体到被碾压完成离开轮体过程中的受力状态变化体现了振荡压实的响应特征，如图6所示，在振荡工作状态下取压实接触点A、压实过程点B、压实离去点C三点处的微观颗粒作为研究对象，3处的受力状态反应了土壤颗粒在压实周期内的受力变化情况。从动振荡轮对土壤颗粒施加作用力如图7所示，图中FM表示振荡轮对颗粒施加的切向摩擦力，大小随轮体的运动规律而变化；Fv表示向前的推动力，Fm表示轮体对颗粒的重力作用；土壤颗粒受到的其他颗粒的摩擦作用力均与轮体施加的作用力相反，图中未标注。

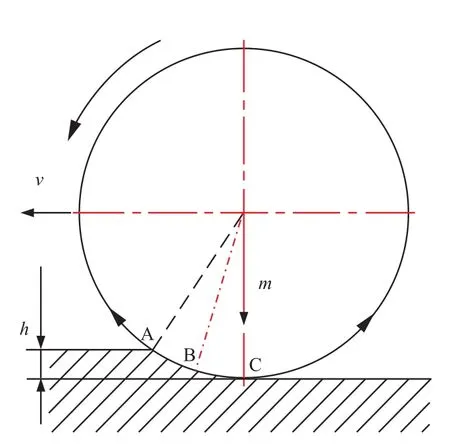
图6 土壤颗粒取点位置

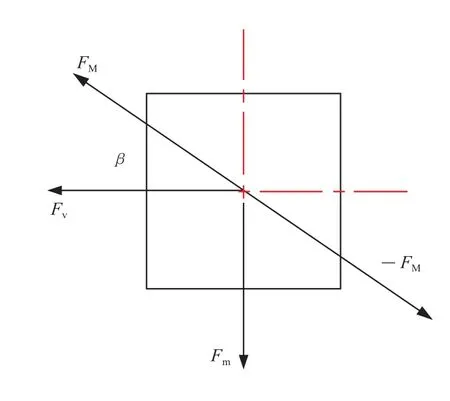
图7 从动振荡轮对土壤颗粒施加的作用力

振荡轮与路面土壤的接触面是圆弧曲面（图6），压实前后产生高度差h，高度差的存在使振荡切向力FM与水平推力Fv之间形成夹角β（图7），随着轮体的滚动前进，压实接触点A发生位移变化，高度差h减小，β值减小，当A点处于离去点C状态时，β值为0，FM水平作用在C点；β值相对较小，FM水平方向的分力对振荡压实作用较大，即“揉搓作用”。FM是切向摩擦力，在土壤级配均匀的条件下摩擦系数恒定，正压力值决定了FM的大小，正压力是Fv与Fm的合力下的分支，接触点A与轮体刚刚接触，处于被压实最高位置，相对于B、C两点，A点处Fv值最大，且Fm处于上升阶段，颗粒在碾压过程中的某点受最大Fm作用，离去点C处Fm最小；因颗粒被碾压下沉逐渐远离轮体中心的水平面，A、B、C三点所受水平推力Fv依次减小。

经上述分析可知，土壤颗粒在压实周期内受到多个方向的作用力，且各个作用力的大小和方向时刻在变化，如图8所示，振荡轮振荡运动周期远小于颗粒压实周期，在压实周期内颗粒受到振荡切向力的多次往复摩擦作用。振荡压实过程中，轮体的振荡运动主要作用在颗粒的水平方向，轮体对颗粒的重力作用主要作用在竖直方向，重力作用是振荡压实的前提，振荡运动加强了重力作用的效果，两者的共同作用能够更加迅速地克服颗粒间摩擦力，促使颗粒产生位移变化，提高压实效率。

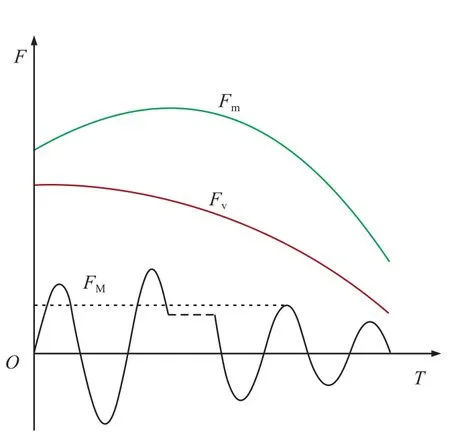
图8 土壤颗粒在压实周期内的受力曲线

当振荡轮作为主动轮时，驱动力矩绕轮体轴芯线驱动轮体转动，轮体与土壤之间的切向摩擦力（驱动力）促使轮体滚动前进，驱动力与轮体对土壤颗粒的振荡切向力FM共线，起到加强“揉搓”压实的作用；主动轮滚动前进过程中或多或少存在滑转现象，滑转现象虽然影响了整车动力性能，但却使轮体与土壤之间产生相对运动，即会产生摩擦力，促使土壤颗粒发生切向位移，同样起到加强“揉搓”压实的作用。压路机作为一种用于提高路面密实度的设备，其主动轮的驱动摩擦作用和不可避免的轮体滑转现象均可加强土壤颗粒的切向运动趋势，尤其对于振荡压路机而言，轮体与路面保持接触有利于提高压实效率。

（3）振荡压实的特点与优势。通过对土壤颗粒振荡响应的分析，并结合振荡运动特征，可知振荡压实具有以下特点。

（a）振荡轮与路面始终保持接触，变向的轮体运动时刻作用于土壤颗粒，可充分利用振荡能量，能量利用率高。

（b）揉搓压实对整机和地面振动影响较小，机器无共振现象存在，驾驶员操作更加舒适。

（c）振荡压实对地面无位移性垂直运动冲击，路面铺层材料无骨料损伤现象。

（d）不会对已压实的路面材料产生松散破坏影响，新旧路面接缝的压实效果较好。

（e）揉搓压实减少了被压实材料内部的“离析”现象，提高了表面层的防水渗透能力，能够获得更好的面层密封效果。

（f）振荡轮对铺层材料的持续揉压作用，对路面铺层具有提浆作用，保证表面平整光滑，提高路面压实质量。

振荡压路机具有压实效率高、压实质量好、节能环保等优势，弥补了振动压路机在施工中产生的负面影响，在桥梁建设、古建筑、城市小区等对振动比较敏感的场合应用较为适宜。尽管压实影响深度相对较小，但这恰好对沥青混合料面层的压实十分有利，事实表明振荡压实对于难以压实的沥青铺层，比如石屑封层、排水沥青、改性沥青SMA等具有较理想的压实效果，对于低温混合料（混合料温度不小于100 ℃时）也能获得理想的压实效果[4]。

振荡压实与其他压实方式的区别

（1）振荡与水平振动。

振荡、圆周振动、垂直振动、水平振动、倾斜振动等名词作为定语修饰压路机，描述的均是压路机轮体的运动特征，其中振荡和水平振动两者常被混淆为同一种运动方式，甚至不少从事压路机设计研究的专业人员在解说振荡运动特征时仍然采用“水平振动”或“水平振荡”作为描述[10]。在混淆理解中最常见的是把振荡和“水平”两字联系起来，误解的根源在于对振荡特征认识不足，认为振荡压实是轮体接地点水平揉搓路面，因而特意增加“水平”作为定语描述。事实上振荡与水平振动的发生机构和外在表现特征都有着本质区别。

振荡压路机是具有往复性扭摆运动特征压路机的专用术语，振荡轮作为整体运动的刚性体绕轮体轴芯往复摆动，振荡发生机构作用于轮体的是交变力矩作用。如图9（a）所示，轮体径向上每个质点的位移大小不同，外圆面上的质点具有最大荡幅，轴芯线处荡幅为零，运动特点类似生活中见到的挂钟钟摆，外圆面接地点运动轨迹呈圆弧状。

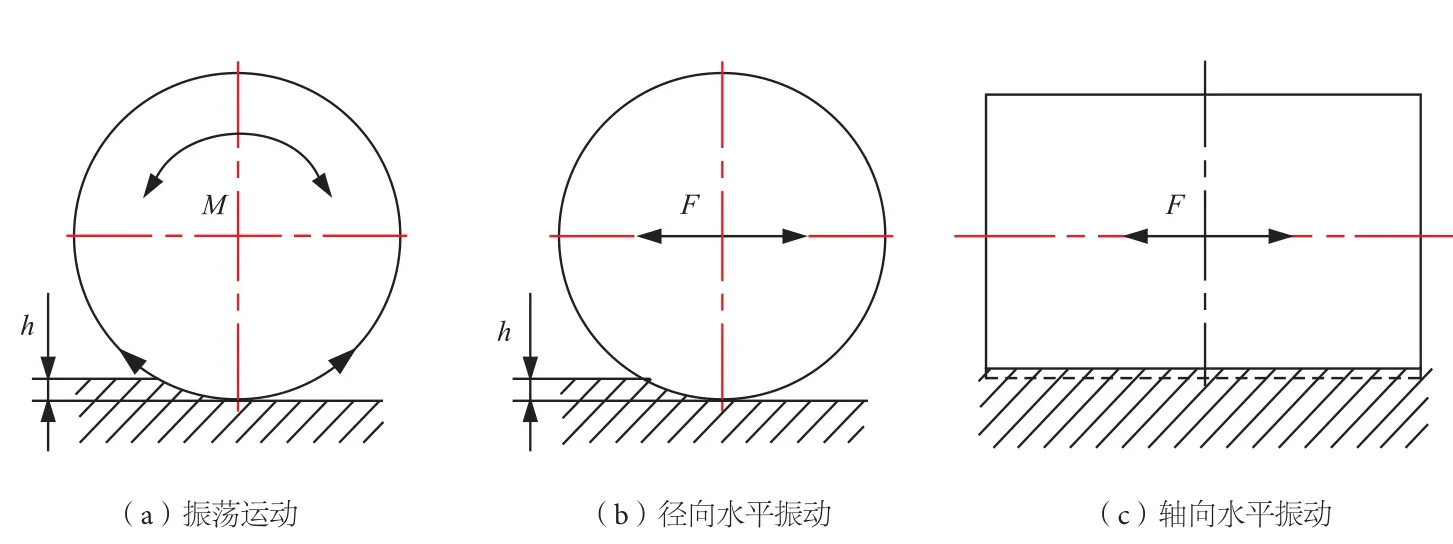
图9 振荡与水平振动运动轨迹曲线

水平振动属于定向振动，应用于压路机属于振动压路机的范畴。按轮体在平行于地面的平面内振动方向的不同，可分为径向水平振动和轴向水平振动，如图9（b）、（c）所示，2种振动形式的轮体都是作为刚性体进行整体运动，振动发生机构作用于轮体的是往复力的作用，参振主体上每个质点具有相同的运动位移（包括大小和方向）。水平振动的方向与地面平行，径向水平振动对土壤颗粒同时施加水平方向的位移性冲击力和摩擦性质的接触作用力，冲击力主要作用在颗粒压实周期前段，摩擦力主要作用在颗粒压实周期后段。轴向水平振动则完全依靠摩擦力作用于路面铺层。宏观上振荡与水平振动的振源激励方式不同，但从微观土壤颗粒的运动响应角度分析，均是通过力的作用增加土壤密实度，只不过不同特征决定了适用于不同场合和铺层材料，殊途同归。

（2）振荡压实与轮胎压实。

振荡压实是振动压实中的特例，轮胎压实属于静碾压实，2种类型压路机最主要的区别在于压轮，振荡轮是能够产生绕轮体轴芯线高频往复运动的刚性体，轮体时刻与路面保持接触，依靠外圆面的切向摩擦力引起土壤颗粒产生运动；轮胎压路机的压轮是可变形的弹性光面橡胶轮胎，压实过程中轮胎同样时刻与路面保持接触，在整机质量的作用下与路面接触部分的轮胎发生弹性变形，轮胎变形扩张产生平行于路面的发散式横向剪切力，进而推动土壤颗粒产生位移性变化，可见2种截然不同的压实方式对路面土壤均有切向“揉搓”的压实作用。

压轮与路面土壤之间的摩擦作用是保证正常压实工作的前提，若无此摩擦作用，圆周振动、垂直振动等这类依靠竖直方向上的位移性冲击压实的设备仍可通过轮体位移施力于地面，但接触性质的切向作用力不复存在，振荡压实与轮胎压实都将变为纯粹依靠重力的静碾压实。振荡轮同时作为驱动轮时，正常范围内的轮体滑转利于剪切土壤，轮胎压轮作为驱动轮时，滑转现象使轮胎产生纵向的弹性变形，轮胎与路面的接触面积较大，具有较好的密封压实效果，弹性轮胎变形后产生的“弹性迟滞”现象可加长轮胎对路面铺层揉搓力的作用时间，利于提高压实效率和压实质量。高频运动的振荡轮将动能转化为土壤颗粒的动能，弹性变形的轮胎将弹性势能转化为土壤颗粒的动能，切向“揉搓”特征决定了振荡压实与轮胎压实对地面作用的深度相比位移性振动压实要小，两种类型压路机应用于路面表层压实更为适宜。

结语

（1）振荡轮利用绕轴芯的力矩作用迫使轮体产生往复性的扭摆运动，轮体滚动前进的“公转”作用对振荡运动的影响只是相位的提前或滞后，对其大小和方向无实质性影响。

（2）名义幅值是在轮体自身保守系统内推导计算得出的理论值，轮体悬空测量值只可检验其设计参数的准确性，名义幅值的不可测量性决定了其定义采用公式描述方式更为贴切。

（3）振动压路机工作振幅大于名义振幅，随着土壤密实度的增加，工作振幅与名义振幅的差值增加；振荡压路机工作荡幅小于名义荡幅，随着土壤密实度的增加，工作荡幅与名义荡幅的差值减小。

（4）工作质量、碾压速度和振荡运动三要素是振荡压实的必要条件，3个参数均可进行量化设计与评估，相互合理匹配可有效提高压实质量和压实效率。

（5）振荡轮与土壤颗粒间的摩擦作用是振荡压实的本质。土壤颗粒在振荡压实周期内受到多个方向的作用力，且各个作用力的大小和方向时刻发生变化，在综合作用力下颗粒被迫发生位移性运动；主动轮的驱动摩擦作用和不可避免的轮体滑转现象加强了土壤颗粒的切向运动趋势，有利于提高压实效率。

（6）振荡压实具有能量利用率高、振动影响小、无骨料压碎现象、平整度较高、面层封层效果好等优势，在道路压实施工中将会起到不可替代的作用。

（7）振荡和水平振动作为定语修饰压路机描述是均是轮体的运动特征，2种压路机发生机构的激励方式和外在运动表现特征有着本质区别，振荡和水平振动无直接联系，属于不同类型的运动方式。

（8）振荡压实和轮胎压实属于不同的压实范畴，相比位移性冲击的振动压实，两者对土壤颗粒均具有切向揉搓作用，对路面铺层影响深度相对较小，应用于路面表层压实更为适宜。

[1] 田丽梅,杨春红,王国安.国内外振动振荡压路机动力学模型[J].吉林大学学报:工学版,2003,33(2):100-103.

[2] 郭克希,黄 樱.基于Matlab/Simulink的振荡压路机参数仿真[J].东华大学学报:自然科学版,2010,36(4):360-362.

[3] 万汉驰.振荡压路机深剖浅析[J].筑路机械与施工机械化,2016,33(9):40-48.

[4] 刘昌仁.日本酒井SW750N复式水平振荡压路机的特点及其应用[J].工程机械文摘,2007(2):9-11.

[5]王连山.悍马HD O120V大型振荡压路机施工两例[J].建设机械技术与管理,2006(8):45-47.

[6] 谭 军,翟丽艳.振荡压路机压实原理及应用[J].东北公路,2003,26(3):143-144.

[7] 晁宇辉.振荡压路机综述[J].建设机械技术与管理,2015,26(8):104-106.

[8] 郝 飞,陆 云,杨 健.振荡压路机名义荡幅的探讨[J]. 筑路机械与施工机械化,2009,26(12):48-50.

[9] 姜右良,黄律钤.振动/振荡压路机名义振幅与振动模型的讨论[J].建设机械技术与管理,2014(3):100-102.

[10] 郑书河,林述温.水平振荡和垂直振动压路机动力学模型研究及展望[J].中国工程机械学报,2011,9(3):278-283.

特稿

为了解决应用煤炭资源所带来的环境污染问题，学者们研发出了洁净煤技术，煤直接液化技术是其中的一种。煤直接液化技术可以生产汽油、柴油、液化石油气以及芳香烃等工业产品，但是会有20%~30%的副产品——煤直接液化残渣（DCLR）。对DCLR的利用程度直接影响煤液化技术的转化效率以及经济性，所以这种副产品备受研究者关注。

本期约稿综述了国内外对于DCLR的高附加值利用方式，重点介绍作为道路沥青改性剂方面的应用；探讨了DCLR和废旧胶粉（RP）的高附加值利用——DCLR-RP复合改性沥青的制备方法和基本性能。结果表明：DCLR-RP复合改性沥青的高温性能和低温性能均比基质沥青有所提高，而且水稳定性也符合规范的要求。因此，DCLR和RP作为沥青改性剂应用于沥青路面，可极大地提高废旧资源的利用率并改善路面使用性能。