电液伺服系统神经网络辨识及控制器设计

韩桂华++王鹏飞++张此军

摘要：针对阀控缸电液位置伺服系统非线性建模问题，采用神经网络进行系统模型辨识。采用LM遗传算法对三层BP神经网络的权值和阈值进行修正，通过训练系统的输入/输出数据建立非线性系统辨识模型。基于此模型，设计模糊PI控制器，利用智能权函数在线自动调整和修改模糊控制器的规则。利用xPC技术建立阀控缸伺服实验台，以实验台阶跃输出信号作为改进BP神经网络辨识信号，以实验台正弦输出信号作为验证信号。实验表明：该神经网络辨识模型的可信性得以验证；通过对比智能权函数模糊PI控制器和模糊控制器的实验曲线，表明前者控制效果更好。

关键词：

改进BP神经网络；系统辨识；智能权函数；模糊控制；电液位置伺服系统；遗传算法

DOI：1015938/jjhust201705004

中图分类号： TP183，TP273

文献标志码： A

文章编号： 1007-2683（2017）05-0018-06

Neural Network Identification and Controller on Electrohydraulic Servo System

HAN Guihua，WANG Pengfei，ZHANG Cijun

（School of Mechanical and Power Engineering， Harbin University of Science and Technology ， Harbin 150080， China）

Abstract：The neural networks system identification was used in nonlinear model on valvecontrolcylinder electrohydraulic position servo system The three layers BP neural network weights and threshold were optimized using LM genetic algorithm， the relationship of system input and output was analyzed and neural network identification model was presented A kind of fuzzy PI controller was designed based on the model， which can automatically adjust and modify the rules of fuzzy controller by using the intelligent weight function A real time electrohydraulic servo test bench was built with the xPC technique The test bench step output was used to identify in the improved BP neural network and the sinusoidal output was used to verify in experiment Experiment results show that the credibility is verified on neural network identification model； and that the control effect of the intelligent weight function fuzzy PI controller is better than the fuzzy controller

Keywords：improved BP neural network； system identification； intelligent weight function； fuzzy control； electrohydraulic position servo system； genetic algorithm

收稿日期： 2016-02-13

基金项目： 国家自然科学基金青年科学基金（51405113）；国家国际科技合作专项资助合作项目（2012DFR70840）

作者简介：

韩桂华（1972—），女，博士，教授，Email：641544105@qqcom；

王鵬飞（1990—），男，硕士研究生；

张此军（1990—），男，硕士研究生

0引言

建立系统的数学模型是控制理论的基础，电液伺服系统因系统的死区特性、增益以及自激振荡等是一个模型参数和结构不确定的非线性系统[1-3]，因此，在工程应用中获得一个与实际系统完全等价的数学模型，并以此为基础进行控制器的仿真设计是非常困难的。神经网络广泛应用于众多领域，但在非线性系统模型辨识中还存在收敛速度慢，学习时间长等问题。本文通过分析标准BP算法现状与存在的问题[4-6]，将BP神经网络结构与遗传算法相结合，建立阀控缸电液位置伺服系统的辨识模型。

模糊控制根据经验制定模糊规则即可对被控制对象实施控制，特别适用于被控制对象是非线性时变的不确定系统。但常规模糊控制器的修正因子α一经确定，其模糊控制规则便不可改变。带有智能权函数的模糊控制器就可以通过智能权函数来在线自调整修正因子α，以达到在线自调整模糊控制规则的目的，从而使模糊控制器能够适应被控制对象的变化[7-9]。模糊控制器由于缺少积分环节，控制过程中还存在稳态误差难以消除的问题。本文以阀控缸电液伺服系统神经网络辨识模型为对象，设计一种智能权函数模糊PI控制器，用于改善和消除系统的稳态误差，实现模糊规则在线自调整，并借助于xPC实时系统的半实物仿真环境和MATLAB软件[10]，验证神经网络辨识模型及模糊控制器的有效性。endprint

1xPC半实物仿真实验环境

利用xPC技术建立的电液伺服实验台的半实物仿真环境如图1所示，在xPC Target环境中，宿主机为装有MATLAB/simulink软件的pc机，目标机为研华工控机，两者通过以太网LAN实现通讯，用于控制器实时测试和系统半实物仿真等。

实验台的动力机构为典型的对称阀控制对称液压缸模型如图2所示，计算机给伺服阀提供控制信号Ur，经过数据输出（D/A）卡、伺服放大器，控制液压缸。为了实现位置闭环控制，由位移传感器把位置信号Us反馈给数据采集（A/D）卡，偏差值ΔU先后经控制器处理和伺服放大器放大，然后以电流信号传递给电液伺服阀，从而控制伺服阀的开口大小，达到通过控制伺服阀的流量变化来控制液压缸位移的目的，同时在示波器和显示屏上显示出液压缸的实时位置。

2基于改进BP神经网络的系统辨识

21LM算法原理

BP神经网络（back propagation neural network）的 BP算法通过信号正向传播和误差反向传播确定权值。在正向传播过程中，输入的信息经由隐含层计算传向输出层。如果输出层得到的信息与期望的输出有误差，误差信号沿原来的神经网络通路反向传播来修正每层神经元的权值与阈值，使网络的误差平方和不断减小。这个过程循环执行，直到输出层的输出达到了期望值，或达到设定学习次数而终止。

标准的BP算法收敛速度慢，学习速率不易确定，很难用于工程实际中。为了优化BP网络，目前常用的优化算法包括变速率算法、共轭梯度算法、高斯-牛顿算法、LM算法等[11-14]。与其他算法比较， LM算法既具有高斯-牛顿法的局部收敛性，又具有梯度下降法法的全局特性，有效改善网络的收敛性能。

当实际输出与期望输出不符时，产生误差用E表示。

E=12∑iK=1e2k（w）（1）

式中： w为网络权值和阈值所组成的向量；

ek（w）为误差。

若wk表示第k次迭代的权值和阈值所组成的向量，wk+1表示第k+1次迭代的权值和阈值所组成的向量。wk+1与wk之间的关系表示为wk+1=wk+Δw。其中权值增量Δw表示为：

Δw=[JT（w）J（w）+μI]-1JT（w）e（w）（2）

式中：I为单位矩阵；μ为用户定义的学习率；J（w）为雅克比矩阵，即

J（w）=

e1（w）w1e1（w）w2…e1（w）wn

e2（w）w1e2（w）w2…e2（w）wn

eN（w）w1eN（w）w2…eN（w）wn（3）

LM算法是为了在以近似二阶训练速率进行修正时避免计算Hessian矩阵而设计的。此雅可比矩阵可以通过标准的前馈网络得到，所以LM算法比梯度法快得多。从式（2）中可知，若μ=0，则为高斯-牛顿法；若μ值很大，则LM算法接近梯度下降法。每次迭代完之后，若减小学习率μ，当期望输出接近实际输出的时候，逐渐与高斯-牛顿法相似。这样就提高了学习速率。

22基于改进BP神经网络实验台的模型建立

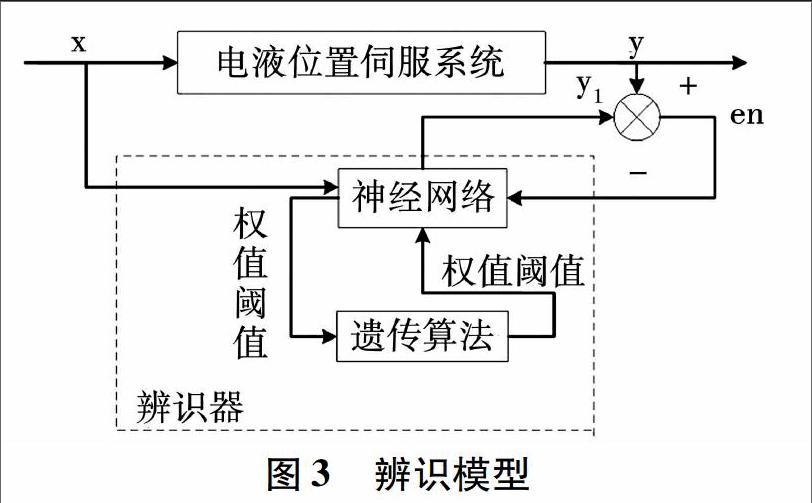
神经网络应用于系统辨识不需要预先选择实际系统的模型，而是直接通过训练系统的输入/输出数据进行辨识。由于神经网络具有非线性的特点，可以不受非线性模型的限制。本文采用典型的三层BP神经网络，再利用遗传算法对神经网络的权值和阈值进行修正，使要求的误差准则函数达到最小，从而优化BP神经网络，最终建立辨識模型，如图3所示。

对位置反馈闭环控制来进行（电液位置伺服系统）辨识。考虑到非线性系统的时变性和干扰性，进行多组实验。分别以正弦信号和阶跃信号为输入，记录其输出数据。这样在xPC实时系统的半实物仿真环境下，在线得到输入输出数据。其中，阶跃信号所得的数据用于改进BP神经网络系统辨识，正弦信号进行验证。

在MATLAB环境下输入nntool，进入神经网络工具箱辨识GUI。将训练样本数据导入GUI，建立神经网络。采用单输入单输出电液伺服系统，确定了改进 BP网络的输入节点数L=10，输出节点数N=1。对于隐含层节点数的选取，经过反复的训练，当M=17时误差最小且精度最高。各层传递函数类型：隐含层选用单极性S型函数，输出层选用线性传递函数purelin，学习算法采用LM算法（trainlm）。采用均方误差（MSE）性能函数网络的误差函数进行修正。创建神经网络如图4所示。

23辨识结果验证

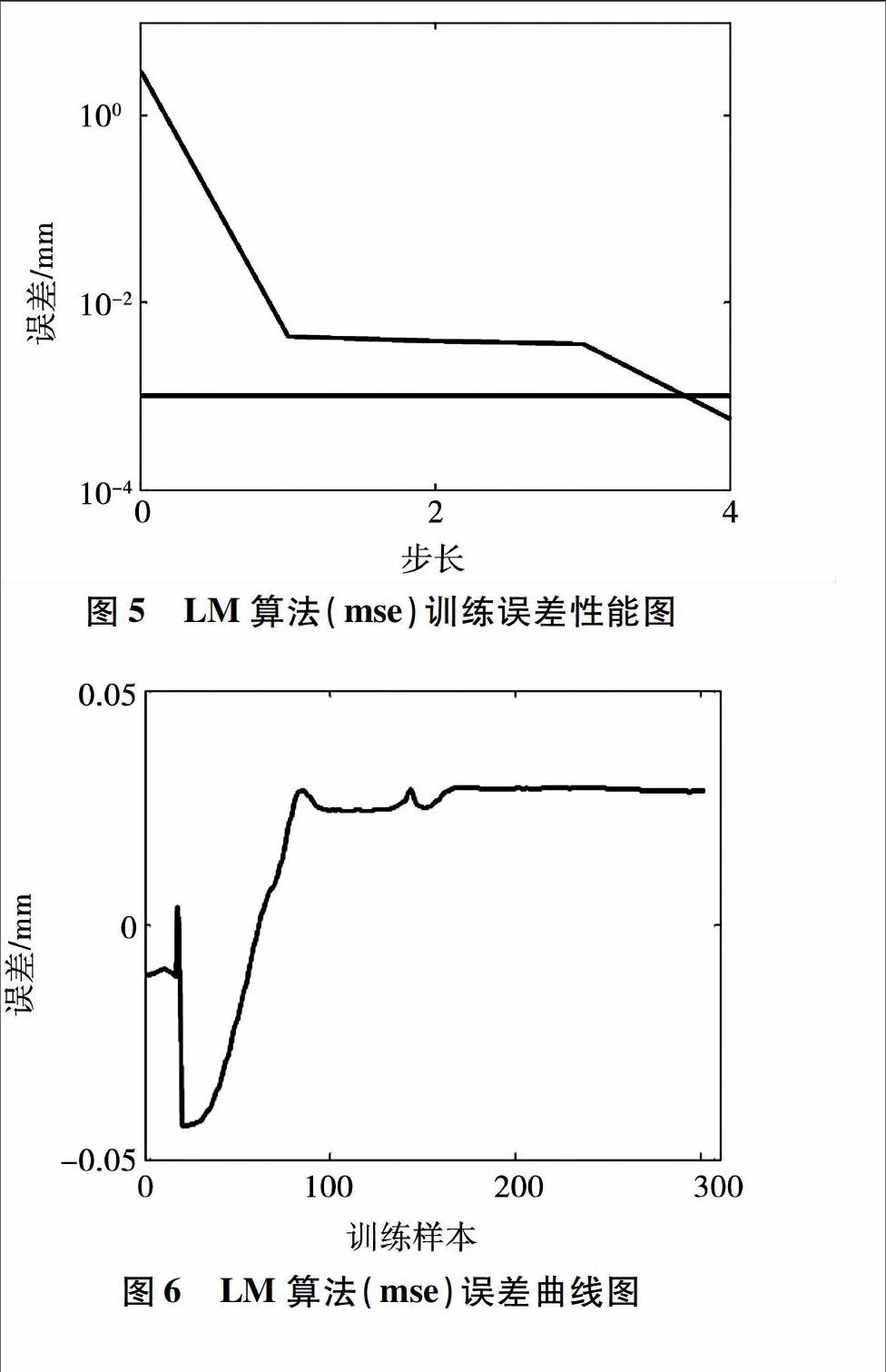
根据建立的神经网络进行辨识，以阶跃信号为输入，LM算法（MSE）性能曲线如图5～图7所示。

将训练误差参数值设为0001，其余均为默认值。得到的训练误差曲线在第四步就达到了所设目标值。训练输出误差曲线比较平滑，说明误差小。

从图7中可以得知，辨识输出与实际输出之间的相关系数都达到了09以上。

根据建立的辨识模型，可对此非线性系统的任何输入进行辨识输出。为下一步针对本系统的控制理论研究提供了前提和保障。

3智能权函数模糊PI控制器

31带修正因子的模糊控制器

模糊控制器常用的是二维模糊控制器，其模糊规则查询表、量化因子Ke和Kc以及比例因子Ku，一旦确定之后，在控制过程中就不能够再改变。因此，需考虑在不同的误差E和误差变化EC等级时，引入不同大小的修正因子，实现模糊控制规则自调整。在误差E较大时，控制的主要任务是消除误差，这时对控制规则中误差E的加权度就应该变大些；而当误差E较小时，此时系统已接近稳态，控制的主要任务就变成了尽快地使系统达到稳定，为了有效地减小超调，就要在控制规则中对误差变化EC的加权度大些，以使误差变化EC所起的作用变大。常用方法有[15]。引入多个调整因子、使用自调整因子和使用自调整函数的方法。本文所使用的智能权函数法是自调整函数法的一种。endprint

由带修正因子α的模糊控制器的自调整原理可知，可利用误差和误差变化的绝对值作为各自的加权，为满足对二者加权之和等于1的条件，误差及误差变化的自调整权函数可分别设计为

αe=|E|/（|E|+|EC|）（4）

αec=|EC|/（|E|+|EC|）（5）

式中E和EC分别为误差和误差变化的模糊值，显然误差的权函数αe和误差变化的权函数αec满足αe+αec=1的条件。

根据式（4）和式（5）所确定的权函数，可以得到智能权函数模糊控制规则的解析表达式为：

U=-<αe×E+αec×EC>（6）

智能权函数模糊控制算法是一种仿人智能控制策略，特点是权函数仅是输入变量的函数，其控制系统可以自动地根据输入变量实时地调整权函数，从而实现在线调整模糊控制规则。为改善控制器的控制性能，消除稳态误差，引入PI控制结构，如图8所示。

32智能权函数模糊PI控制器的设计

在MATLAB中利用模糊推理系统 （FIS） 编辑器，构造一个双输入（偏差E和偏差变化EC）、单输出（控制量U）的二维模糊控制系统。采用Mamdani型推理方法，其中模糊逻辑的and算法采用“prod”，or算法采用“probor”，清晰化算法采用“centroid”，蕴含算法采用“prod”，综合算法采用“max”。

模糊输入变量（E和EC）和输出变量（U）的隶属度函数均采用高斯型隶属度函数。论域及语言值分别如下[16-20]：

偏差E的论域及语言值为：

{负，零，正}={n，z，p}={6，5，4，3，2，1，0，1，2，3，4，5，6}

偏差变化EC的论域及语言值为：

{负，零，正}={n，z，p}={06，05，……，01，0，01，……，05，06}

控制量U的论域及语言值为：

{负大，负中，负小，负，零，正，正小，正中，正大}={nb，nm，ns，n，z，p，ps，pm，pb}={6，5，4，3，2，1，0，1，2，3，4，5，6}。

输入变量和输出变量的模糊子集隶属度函数如表1所示。

电液位置伺服系统主要是通过控制电液伺服阀的阀门开口大小和速度来达到控制液压缸活塞的位移的目的，根据知识和经验归纳可总结出9条模糊控制规则。模糊控制规则如表2所示。结合智能权函数的原理，在MATLAB/Simulink环境下建立智能权函数模糊PI控制系统的仿真图，如图9所示。

33实验分析

为了验证基于神经网络辨识模型所设计的智能权函数模糊PI控制器在实际应用中的有效性，在xPC半实物仿真实验台上进行了实时控制实验研究。

实验时将智能权函数模糊PI控制器与常规模糊控制器进行比较研究，其阶跃响应和正弦响应的实验结果曲线分别如图11和图12所示，图中曲线1为输入，曲线2为模糊控制输出，曲线3为智能权函数模糊PI控制器输出。由图可见，模糊控制器和智能权函数模糊PI控制器的稳态性能和跟踪性能都表现得不错。但是模糊控制由于没有引入积分项，阶跃响应曲线有余差存在，而智能权函数模糊PI控制器几乎没有余差，并且阶跃响应的上升时间更快、超调量更小，正弦响应时其跟踪响应时间更短。

4结论

本文以电液伺服实验台为例，通过xPC半实物仿真采样获得被控对象的输入输出数据，将BP神经网络结构与遗传算法相结合，建立了基于LM算法的神经网络辨识模型。实验表明通过在神经网络外部拟合系统的输出，对本质非线性电液位置伺服系统进行辨识，调节网络内部的权值获得的神经网络辨识模型可信性好。以此模型為对象，结合智能权函数的作用原理，利用MATLAB/Simulink设计了一种智能权函数模糊PI控制器。这种控制器能够通过在线自调整修正因子α来在线自调整模糊控制规则，改善了常规模糊器不能很好地适应控制对象的变化的缺点。与常规模糊控制器相比，智能权函数模糊PI控制器的控制精度更好。

参 考 文 献：

[1]GIOVANNELLI F，GIREMUS A Bayesian Noise Model Selection and System Identification Based on Approximation of the Evidence[M].Statistical Signal Processing （SSP）， 2014 IEEE Workshop on， 2014：125-128

[2]LING T G， RAHMAT M F， HUSAIN A R Anfis Modeling of ElectroHydraulic Actuator System[C]// Signal Processing and its Applications （CSPA）， 2012 IEEE 8th International Colloquium on 2012：89 – 92

[3]LING T G， RAHMAT M F， HUSAIN A R System Identification and Control of an ElectroHydraulic Actuator System[C]// Signal Processing and its Applications （CSPA）， 2012 IEEE 8th International Colloquium on IEEE， 2012：85-88

[4]谢蓄芬， 刘泊， 王德军 一种改进BP神经网络在模式识别中的应用[J]. 哈尔滨理工大学学报， 2004（5）：63-65

[5]YU F， XU X A Shortterm Load Forecasting Model of Natural Gas Based on Optimized Genetic Algorithm and Improved BP Neural Network[J]. Applied Energy， 2014， 134（134）：102-113endprint

[6]LIU Y Y， SHEN D R， CHEN Y J Multiinnovation Stochastic Gradient Identification Algorithm Based on Feedforward Neural Networks [J]. Journal of Harbin University of Commerce： Natural Sciences Edition， 2006，22（2）： 83-86

[7]李劲松，金志扬 基于修正因子智能权函数的汽车ABS模糊控制算法仿真研究[J]. 汽车科技，2010（3）：55-57

[8]IZADIKHAH M Deriving Fuzzy Weights of Criteria from Inconsistent Fuzzy Comparison Matrices by Using Goal Programming Method [J].Journal of Intelligent & Fuzzy Systems Applications in Engineering & Technology， 2013， 25（1）：69-80

[9]黄强， 张晓， 张胜强 油压跟随性的智能权函数模糊控制研究[J]. 九江学院学报， 2009， 28（3）：6-8

[10]张立勋， 董玉红， 王怀军 基于半物理仿真技术的机电伺服系统模型辨识研究[J]. 机电一体化， 2006， 12（2）： 30-32

[11]JIANG B， WANG B Parameter Estimation of Nonlinear System Based on Genetic Algorithms [J]. Control Theory & Applications， 2000， 17（1）：150-152

[12]张本国， 李强，王葛 基于改进BP神经网络的连铸漏钢预报[J]. 中国机械工程，2012（2）：204-207

[13]尹光志，李铭辉，李文璞 基于改进BP神经网络的煤体瓦斯渗透率预测模型[J]. 煤炭学报，2013（7）：1179-1184

[14]高雪鹏， 丛爽 BP网络改进算法的性能对比的研究[J]. 控制与决策，2011， 16 （2）： 167-171

[15]WANG Chihsu， HUNG Kunneng Dynamic System Identification Using Highorder Hopfield Based Neural Network [J]. Asian journal of control 2012， 14（6）： 1553-1566

[16]温嘉斌， 麻宸伟 无刷直流电机模糊PI控制系统设计[J]. 电机与控制学报， 2016， 20（3）：102-108

[17]于舰，孙桂涛，高炳微 液压四足机器人驱动器 CAN 总线通信[J].哈尔滨理工大学学报，2013，18（2）：78-80

[18]XU Baochuang， ZHANG Yingying An Improved Gravitational Search Algorithm for Dynamic Neural Network Identification [J]. International Journal of Automation and computing， 2014， 11（4）：434-440

[19]荣盘祥， 董文波， 于林 混沌自调整模糊PID控制器的研究与应用[J]. 哈尔滨理工大学学报， 2014， 19（2）：26-30

[20]雷宾宾， 保宏， 许谦 區间二型模糊 PI/PD 控制器设计与结构分析[J]. 电机与控制学报， 2016， 20（6）：50-63

（编辑：关毅）endprint