基于MATLAB的齿轮箱油路模拟计算

文 | 陈晓爱，王晓东

基于MATLAB的齿轮箱油路模拟计算

文 | 陈晓爱，王晓东

在通用工业齿轮箱设计中，润滑油路的计算更多源自经验；但对于高可靠性要求的风电齿轮箱而言，润滑油路的精确计算是必不可少的，实际经验表明，理论计算的难度和工作量都比较大，借助软件计算相对精确且所需时间较少；可进行流体计算的大部分软件，如Fluent、Abaqus有限元软件等，因需要完成立体建模、划分网格等耗时耗力的工作，从时间上来说并不经济，因此本文采用以数学模型计算的软件MATLAB（版本R2010b）为例进行油路模拟计算的探讨。

MATLAB是MathWorks公司出品的商业数学软件。Simulink模块是MATLAB最重要的组件之一，利用该模块可以很方便地实现可视化仿真，并且无需完成立体建模和网格划分，只需要完成框架化的数学模型搭建即可。本文借助此模块搭建两个简单的油路模型，并与人工理论计算进行比较；在此基础上，计算一个具体的工程案例，利用试验测得的结果，验证此计算模块的应用性。

模拟计算的基础条件

计算前，先要明确一些计算条件。在油泵工作稳定、温度达到平衡的情况下，整个风电齿轮箱的油路中润滑油的流动属于定常流动。

风电齿轮箱常用润滑油为VG320，密度约为800kg/m3，齿轮箱油温60 C时，运动粘度ν约为110mm2/s，整个油路的高度差一般不超过0.5m，重力造成的最大压力差＝ρgh＝3920Pa＝0.00392MPa，而油路最小的油压ΔPmin≥0.1MPa，重力对油路的影响远不如油压；为了简化计算过程，忽略进出口以及各支路的高度差。

理论计算和软件计算的比较

在以上基础情况下，油路计算时会碰到两种压力损失形式，即沿程压力损失和局部压力损失。以下对两种损失形式理论计算和软件计算的结果进行比较分析。

一、沿程压力损失的计算比较

假设整个油路都是细长管路，无弯管、阀口等，这样仅需计算沿程压力损失。根据《液压与气压传动》（华中科技大学出版社第三版），光滑的金属圆管临界雷诺数Recr＝2320；根据ISO/TR 18792 Lubrication Of Industrial Gear Drives，直管中的油流速度υ推荐不超过3m/s。那么以管径d＝10mm为例，直管油路的雷诺数Re为：

因此，风电齿轮箱直管油路可以按层流计算。现通过简单地对比计算来说明建模计算过程：

（一）理论计算

例1：按总流量Q＝100L/min，动力粘度μ＝110×10-6×800＝ 8.8×10-2Pa·s，第一支路 d1＝ 10mm、L1＝100mm，第二支路d2＝15mm、L2＝400mm；

假设两支路为层流，则总流量：

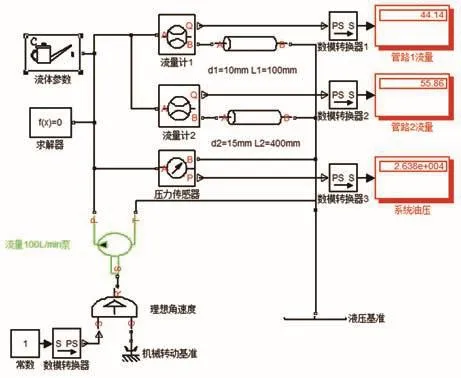
图1 例1在Simulink中的计算模型图

d为油管直径，μ为润滑油动力粘度，L为油管长度，ΔP为入口和各出口的压力差（因忽略各支路的高度差，因此这里各支路ΔP相同）。

计算可得：ΔP＝2.64×104Pa，q1＝44.14L/min，q2＝55.86L/min

经比较，两支路的雷诺数Re均小于临界雷诺数Recr，属于层流，因此计算结束，不需要复杂的迭代计算。

（二）软件计算

Simulink中建模过程：（1）常数1经数模转换器变为1rad/min；（2）经理想角速度变换，参考转速为零的机械转动基准，形成100L/min泵的输入；（3）100L/min泵分成两个管路d1和d2完成油路循环；（4）油路中加入流体参数、求解器；（5）各管路中加入流量计，经数模转换输出流量值，其中主管路加入压力表，同样经数模转换，输出油压值。

从Simulink的计算结果来看，其结果和理论计算完全一致。

此模型比较简单，如果同一支路中管路直径发生变化，理论计算的方法是用公式把不同直径的管路转化为同一直径的等效长度代入计算。

需要注意以下两点：

（1）Simulink的模拟中，因关注的是定流量下管路的流量分配，故设泵的体积效率和总效率为1，即100%。

（2）如果直管中的实际雷诺数Re超过临界雷诺数Recr（风电齿轮箱行业很少见），理论计算的难度会非常大，需要借助莫迪图做迭代计算，软件计算的优势会非常明显；不过本行业中的直管流动一般都是层流，因此本文对此不作更多说明。

二、局部压力损失的比较

（一）理论计算

相对于沿程压力损失，由于造成局部压力损失的结构多种多样，局部压力损失的计算要相对复杂得多，这里举油路计算中最常见的两种类型：薄壁小孔和90 º弯管。

例2：按总流量Q＝100L/min，运动粘度μ＝110×10-6×800＝ 8.8×10-2Pa·s，第一支路 d1＝ 20mm、L1＝100mm，第二支路d2＝20mm、L2＝100mm，同时第一支路有一个20mm的90弯管，其弯曲半径r为60mm，第二支路有一个直径为4mm节流孔；

（1）对薄壁小孔，液压教材中的公式见下：

其实此公式有一个隐含的应用条件，即雷诺数Re>Recr（临界雷诺数），达到紊流状态；如为层流状态，计算公式反而不同，详细见MATLAB的“Fixed Ori fi ce”帮助条目。

为此首先要确定薄壁小孔的临界雷诺数，MATLAB给出建议值为12，但各教材和手册中未给出具体值。

薄壁小孔和锥阀阀口结构接近，临界雷诺数Recr处于20－100的范围（表1）；在实际Re明显大于此范围的情况下，具体取值可取MATLAB推荐值12，也可取锥阀阀口的平均值60。

另外公式中Cd为小孔流量系数，液流不完全收缩时，Cd≈0.7－0.8，这里取0.7。

（2）对90 º弯管的局部损失，液压教材中的公式见下：

根据《液压流体力学》（国防工业出版社），局部损失系数ζ按流态的不同分为层流区、光滑管区、阻力平方区，这几个区域里ζ的取值也不相同，但在层流区和光滑管区的取值均需靠实验确定，无实用意义；实际上流体流经局部障碍时，Re很小就可以使局部损失系数进入阻力平方区，此时，ζ只决定于局部障碍的结构形式，相关的液压手册上列出的ζ值实际上是阻力平方区的ζ值。

MATLAB则对此问题作了简化，仅把流态分为层流区和紊流区，紊流区的计算和上述一致；关于层流区的计算，MATLAB在上述公式中增加了系数：Recr/Re。为使计算结果更符合实际情况，对于90º弯管的临界雷诺数，取值应尽量在实际雷诺数之下（推荐小于200），并把紊流作为流体流态。

表1 常见液流管道的临界雷诺数

参考《Flow of Fluids Through Valves, Fittings and Pipe TP-410M》（[美]CRANE工程部 编）附件A-26，局部损失系数ζ即此文献中的K（r为弯曲半径，d为油管直径，见图2）取值如表2所示。

其中fT可按上述参考文献的列表取值，见表3。也可按上述参考文献中的公式计算：

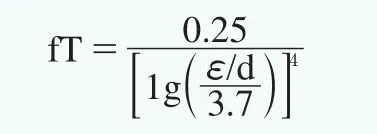
式中的ε代表管壁的粗糙度；需要注意的是：在MATLAB中ε采用了固定值，即全部为洁净商业用钢管的管壁粗糙度0.05mm。

可计算如下：

由q1＋q2＝100L/min，解此二元二次方程组可得：

（二）软件计算

在MATLAB中建立的模型与计算结果如图3所示。

可知模型的计算结果和理论计算非常接近。需要注意的是无论是理论计算还是在MATLAB中模拟，局部损失的计算都很难与实际情况完全一致，因为在此类计算中，难以考虑到相邻局部损失之间的干扰：在相邻局部损失之间距离较小的情况下（通常为直管直径的20倍），两个局部损失之间有相互的扰动，计算结果往往比实际情况理想。

设计实例

以上计算演示了油路计算的基本类型，在管路复杂的情况下，理论计算几乎是不可能的，MATLAB的使用简化了计算工作量。

表2 90弯管和法兰或对焊连接90弯头的阻力系数

图2 弯曲半径

图3 例2在Simulink中的计算模型图

表3 洁净的商用钢管在全紊流区的摩擦系数

工程中，如果要得到齿轮箱润滑流量的精确结果，可以在齿轮箱装配完毕后，在管路中接入各类电磁/超声流量传感器；不过由于成本高以及装配后不便于调整，很少使用这种测试方法。通常做法是仅装配必要的壳体、管路和相关的润滑系统部件等，通入一定温度的润滑油后测量各个润滑点的油量，并与设计值比较，以此来调整各个润滑点的油量大小。

针对某兆瓦级一级行星两级平行轴结构的风电齿轮箱，首先使用Simulink模拟计算流量（图5），然后按图4所示的装配形式实测了各润滑点的流量，将两者进行对比，来验证Simulink的计算结果。图5为软件中模拟计算的结果，表4为模拟计算和实际测量的结果对比。

对图5所示管路作简要说明。

系统总流量Q＝105L/min，动力粘度μ＝110×10-6×800＝8.8×10-2Pa·s，共有15个位置的润滑点（部分位置8、13、15润滑点分为2个）；其中：

位置1和位置3在三通1处分开，分别流经各自的直管、弯头、弯管、小孔后达到润滑位置；

位置2和位置4在三通2处分开，分别流经各自的直管、弯头、弯管、小孔后达到润滑位置；

位置5、6、11、12单独流经各自的直管、弯头、弯管、小孔后达到润滑位置；

图4 左图，测试流量时装配情况示意图；右图，油管三维模型

表4 试验和Simulink软件计算结果对比

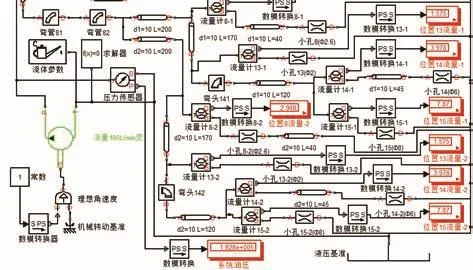
图5 某兆瓦级齿轮箱油路在Simulink中的计算模型图

位置7、9、10流经共同的直管、弯头、弯管部分后，分别流经各自的直管、弯头、弯管、小孔后达到润滑位置；

其余位置均流经共同的直管、弯头、弯管部分后，分别流经各自的直管、弯头、弯管、小孔后达到润滑位置。整个管路在模拟计算中无泄漏。

由表4可看出，大部分润滑点油量误差在±5%以内，只有少数流量较低的支路结果大于5%，油压的计算结果相比测量结果略高。考虑到测量误差和相邻局部损失之间的干扰，这样的结果对风电齿轮箱的油路计算已经足够。

结语

结合以上计算与应用实例可知，与人工理论计算相比，采用MATLAB模拟计算风电齿轮箱的油路，准确度高，不再依赖个人经验，尤其在新设计、无类似油路设计经验的情况下，非常有效；对比其他流体计算软件如Fluent、Abaqus等，只需要搭建框架化的数学模型，不需要做复杂的立体建模、划分网格、后处理等工作，因此总的计算时间较少。可以说，MATLAB的油路模拟计算同时具备了准确性高和工作量少的特点，非常值得在实际工作中推广应用。

（作者单位：陈晓爱：苏州吾纳德传动技术有限公司；王晓东：新疆金风科技股份有限公司）

摄影：王志远