异步电动机最大效率转矩比控制方法

王 艳， 赵换丽

(平顶山学院 电气与机械工程学院，河南 平顶山 467000)

异步电动机最大效率转矩比控制方法

王 艳， 赵换丽

(平顶山学院 电气与机械工程学院，河南 平顶山 467000)

针对传统异步电动机直接转矩及直接磁链控制中未考虑电动机效率的问题，提出异步电动机最大效率转矩比控制方法。此方法将定子磁链作为控制对象，并联合电动机损耗模型给出磁链在线计算方法。在线磁链计算是根据电动机的实时工况给出最佳磁链参考值，而参考值的给定依据是当前转矩下的效率最大，所以所提方法可应用于直接转矩或直接磁链控制系统中。而电动机损耗模型对参数具有依赖性，同时在线计算不利于工业应用，因此通过实验方法建立了一组特定温度下的多速域不同负载下的离线表。实验结果表明,所提出的算法具有可行性，尤其在轻载工况下效率提升明显。

异步电动机； 最大转矩效率比控制； 定子磁链； 直接磁链控制

0 引 言

提高系统效率是电气控制中较为重要的思想，而电动机作为电能消耗的主体，提高电动机效率尤为关键。异步电动机作为可调速设备中的核心部件，一直广泛使用在各类传动场合。尽管永磁同步电动机的出现从电动机本体上改变了其效率低下问题，但同时材料成本大幅上升[1-2]。加之近年稀土材料价格一路走高，导致人们重新将研究聚焦到异步电动机上，甚至将其应用到电动汽车中[3-4]。文献[5]中研究了异步电动机弱磁运行时的效率问题，但是基速以下尤其是轻载工况下的效率提升意义更加明显。

异步电动机控制中的效率提升可通过改变不同负载下对应的磁链大小而实现[6]。文献[7]中指出有3类方法可实现电动机磁链的实时控制以降低电动机损耗并提高效率。第1类方法是控制电动机某个单一变量如基波功率因数或转差频率[8-9]。此类方法鲁棒性强、参数依赖性低，通用于标量及矢量控制，但精度相对较低，广泛应用于动态性能要求较低的场所。第2类最大效率控制方法基于搜索算法，电动机磁链通过不断的迭代以实现当前工况下输入功率最低[10-12]。搜索法虽然不依赖电动机参数，但是动态性能差，难以应对频繁调速或变载场合。第3类方法基于电动机损耗模型，因此对参数具有依赖性，但适用于矢量控制系统，系统动态性能好。文献[13]中使用神经网络算法分析了电动机的损耗模型，但是未证明此方法在不同负载下的适用性。近期文献[14]中指出,采用端口受控哈密顿理论控制电动机损耗最小化，但是文章假定损耗电阻为定值。

本文提出一种应用于异步电动机基速以下任意工况下的最大效率转矩比控制算法。采用的为控制电动机的单一变量以实现损耗最小化的第1类控制策略。不同于已有策略，本方法选取定子磁链为控制对象，并结合了第3类策略中的电动机损耗模型，因此所设计的控制方法适合电动机直接转矩控制及直接磁链控制。同时为了提高工业应用的可能性，将在线计算转化为离线表。实验结果表明，所提出的控制算法以及建立的离线表能够明显提高电动机轻载时的效率。

1 异步电动机模型及其损耗分析

1.1异步电动机模型

异步电动机建模分析中的几种参考坐标系如图1所示。图中给出了静止坐标系(α,β)、旋转坐标系(d,q)、转子磁链旋转坐标系(dm,qm)以及定子磁链旋转坐标系(ds,qs)。

图1 异步电动机及其参考坐标系定义

在dq旋转坐标系下对电动机进行稳态建模，则其等效电路如图2所示。

在此等效电路中，电动机处于稳态运行状态，则s表示转差率；σ为漏电系数；Ls为定子电感；Lm为励磁电感；Lr为转子电感，转子耦合系数kr=Lm/Lr。电动机热损耗由定转子电阻(Rs和Rr)产生，而铁芯损耗用铁芯等效电阻Rfe表示。为了简化计算过程，本文忽略机械损耗、负载杂散损耗以及逆变器输出的附加损耗。则异步电动机的电磁模型可表达为：

(1)

式中：L1s，L1r分别为定转子的漏感；φm为励磁磁链；im为励磁电流。

图2dq旋转坐标系下异步电动机等效电路原理图

以上模型中考虑了由励磁电流引起的磁饱和问题，而定转子漏感认为是定值。假定电动机运行在稳态状态，则定子磁链分量和电流分量以及电压分量的关系分别如下式所示：

(2)

udq=Rsidq+(-edq)=Rsidq+jωφ

(3)

式中

则电动机的电磁转矩、同步转速、转差分别为：

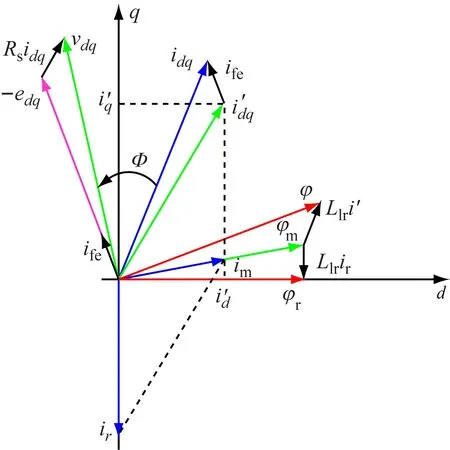
图3 稳态旋转坐标系下的矢量关系图

(7)

1.2效率计算

如图2所示，电动机的机械损耗、负载杂散损耗、逆变器附加损耗等都已被忽略，因此,电动机损耗只计其定转子发热以及磁通基波引起的铁损，即：

(8)

(9)

则电动机总损耗为：

Ploss=Pj+Pfe

(10)

因此,稳态状态下的电动机效率可表达为：

(11)

式中，Pm=T·ωm表示总输出机械功率。

由上分析可知，任何包含损耗模型的控制策略都必须考虑电动机的温度和转速。此外，也必须考虑铁损电阻Rfe与磁通大小间的关系。

2 铁损建模及估算

电动机运行时，其铁损主要由磁滞损耗和涡流损耗引起，其中磁滞损耗的计算公式为[15]：

(12)

式中：V表示铁芯总体积；f为工作频率；Bmax是铁芯中磁通密度的峰值；n和χ是与材料相关的常量。

由式显然可知磁滞损耗的计算需要依赖电动机结构参数以及材料参数。因此引入一个新的常量：

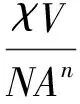
(13)

式中：A表示磁通穿过的截面积；N为绕组匝数。此常量包含了所有与电动机参数相关数据，则式可以改写为：

PHy=kHyfλn

(14)

式中，指数n是与电动机转子材料有关值[13]。本文研究的电动机硅钢材料为M400 65A。由此式可知磁滞损耗与转子磁链相关，与磁通无关，而转子磁链大小可通过观测器获得。

同样的，涡流损耗PEC也与电动机几何参数相关，其计算公式为：

(15)

式中：d为叠片厚度;ρ为磁性材料的电阻率。

类比前文可得，涡流损耗公式同样可以通过定义涡流损耗常数kEC进行简化得到，其中,kEC的定义为:

PEC=kECf2λ2

(16)

(17)

综上可知，电动机铁损为磁滞损耗和涡流损耗之和，即：

PFe=PHy+PEC=kHyfλn+kECfλ2

(18)

本实验中的电动机参数如下：功率为2.2 kW，转矩为15 N·m，电压为400 V，Rs=3.37 Ω，电流为5.08 A，Rr=2.2 Ω，频率为50 Hz，Lls=16 mH，转速为1 400 r/min，Llr=16 mH。据此参数可以计算出kHy=1.591，kEC=0.017 8以及n=1.432，则根据工作频率和输入电压可以实现铁损的计算。另外，铁损也可通过电动机空载实验测量，为了验证以上计算公式的精度，设计了5种频率下的铁损测量实验，所得数据结果如图4所示。同时图4绘制了式在不同频率下的损耗函数曲线，可见此函数计算具有很高的准确度。因此采用式进行在线铁损计算是准确可行的。

图4 5种不同频率下铁损的实验结果及函数曲线

3 基于定子磁链的最大效率转矩比算法

电动机稳态运行时的主要输出指标有转矩、转速以及温度，最大效率转矩比的根本目标是通过优化定子磁链以提高电动机输出效率。其目标磁链φMEPT是通过离线计算获得。

本算法需要将最大电流信号Imax作为输入信号，最大电流为逆变器输出电流限制或过载电流限制。在(id,iq)描述的坐标系中，第1象限表示m×n阶电流向量矩阵，则任意可表示为：

(19)

定子电流幅值处于0～Imax之间，同时电流角处于最小角度至90°电角度之间，如图5所示。

图5 dq旋转坐标系下电流矢量及运行区域图

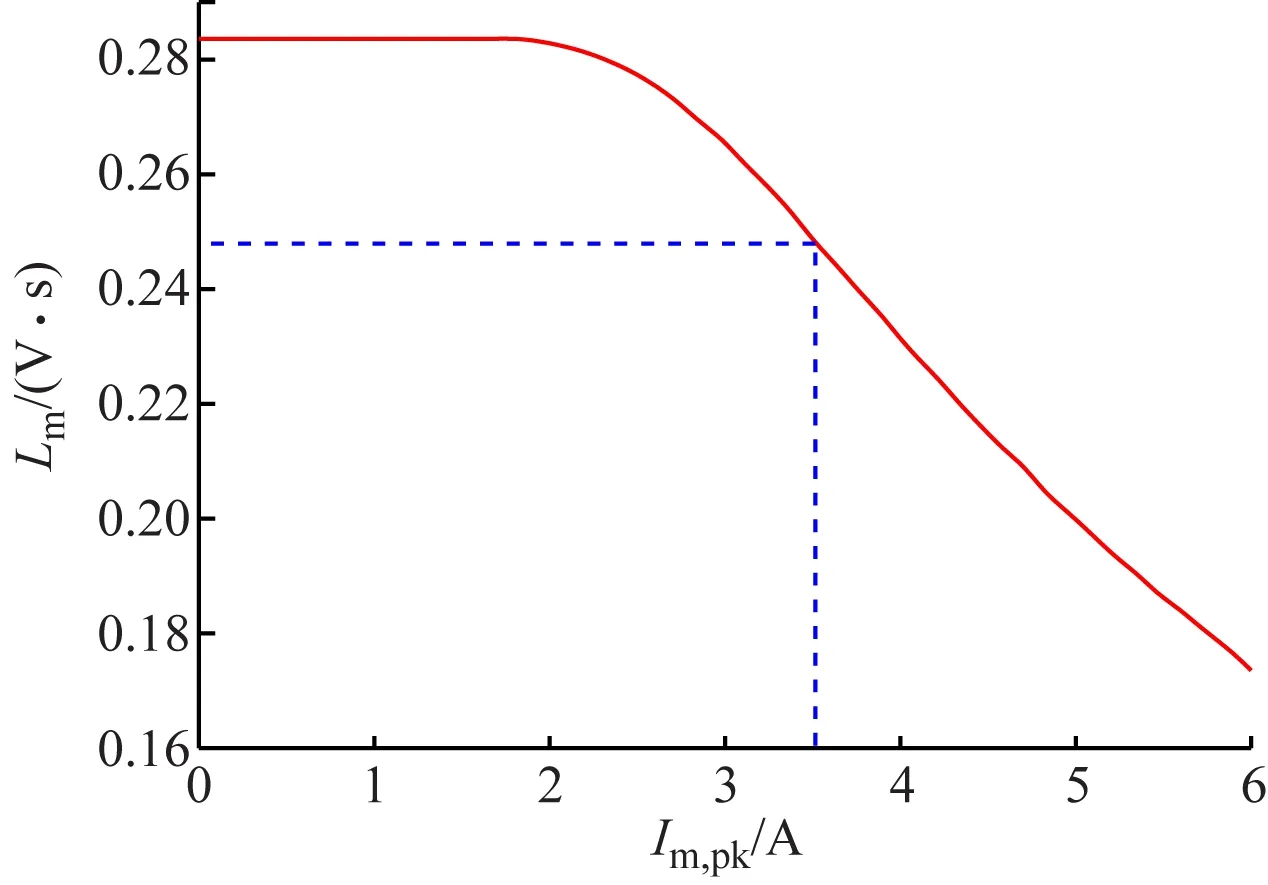
图6 磁阻与励磁电流幅值的变化关系

对于给定的电动机转速，其电子转速可以很容易的通过式(5)计算。当电动机工作温度已知时，电动机的反电动势、总定子电流、机械损耗以及效率都可通过式(3)、(8)～(11)获得。

对于给定的定子电流幅值I(m)，电流矢量i′(m,n)是与位置信号θi(n)相关的变量，在限定的映射区域中变化，其映射过程已如前文(式(19)以及图5)所述，优化定子磁链可以通过最大效率转矩比控制实现。MEPT控制方法选取φMEPT(m)对应于此工况下的最大效率点。对于任意给定的转速和转矩，一个最优磁链参考值即被用以计算实时铁损大小。

重复执行以上步骤，计算出0～Imax之间所有的m个点即可生成MEPT算法下的二维查表结果。由于最大效率对应的最优磁链与电动机转速和温度有关，故实际工程中需要针对电动机的转速和温度建立三维查表以提高电动机控制精度。本文中，最优磁链的获取是通过对给定转矩和转速值进行插值拟合实现的。转矩与磁链的关系共对32个点进行数据计算。

针对本实验中采用的2.2 kW异步电动机，通过空载实验获得的励磁电感与峰值励磁电流的变化关系见图6。最大励磁电流峰值设为6 A，而额定定子励磁电流为3.5 A。

MEPT控制算法采用实时最优磁链控制，与定磁链控制算法下的热损耗及铁损对比如图7所示。图7所示结果在1 000 r/min转速下测得，因为额定转速下其曲线走势相似，所以没有额外展示。实验在25 °C室温下测得，对应电动机工作温度约为40 °C。磁链值的大小参考实验测得的图4中的结果。

图7 额定转速下损耗与转矩的关系

与期望一致，在电动机轻载时其效率提升较为明显，同时电动机效率提升与电动机转速相关，如图8所示。结合图7可知，在电动机轻载时采用MEPT控制同时降低了电动机的铁损和热损耗。由图8可知，当电动机半载时效率提升约6%，而1/3负载时效率提升达到10%。相反地，当负载超过额定转矩时效率并不能有明显提升。其原因在于当负载超过额定值时，电动机需要更高的励磁来驱动，其磁链与转矩的变化关系如图9所示。

图8 不同磁链下转矩和效率实验结果对比

图9 不同转速下磁链与转矩的关系

电动机运行中的温度变化也是影响其状态参数的一个重要因素，通过实验测量了一组转速为1 000 r/min时温度对电动机MEPT控制中最优磁链参考值的影响，结果如图10所示。由图可见，电动机负载对磁链参考值影响远大于温度对其产生的影响，但随着温度的升高，磁链参考值略有增大。因此，为了简化控制算法，在非高温运行时可将40 °C对应的磁链变化曲线作为离线查表通用规则。

图10 转速为1 000 r/min时磁链与转矩和电动机温度的关系

4 直接磁链矢量控制策略

异步电动机直接磁链控制系统框图如图11所示，此控制系统框图同样适用于直接转矩控制，因为两者都是调节磁链的控制方式。

图11 直接磁链控制系统框图

直接磁链矢量控制系统是结合了直接磁链观测器的快速性以及矢量控制中电流观测器的稳定性。定子磁链直接通过ds轴电压进行控制，与qs轴分量无关。由于PI调节器中的增益值不会造成磁饱和,故磁链闭环中的带宽可以很高。通过控制PI调节器的ds轴电流分量实现对转矩的控制，因此,其输出结果为ds轴电压分量。

直接磁链矢量控制系统的核心结构如图12所示，图中的参考磁链由MEPT算法产生，MEPT算法通过对输入转矩和转速进行计算后输出最优磁链值以保证电动机效率最大化。同时为了保证转矩动态性能，直接磁链控制器实现了最大转矩输出时可接受的转矩响应，则在轻载时动态响应更加快速。

图12 直接磁链系统控制框图

5 实验分析

实验对象为一台2.2 kW的异步电动机，使用伺服永磁电动机对其进行加载，中间连接了转矩测量装置以便获取电动机输出的机械功率大小，装置结构图如图13所示。实验中异步电动机工作在转矩模式，因其转速受控于永磁电动机。电动机的输入电功率和输出机械功率均通过功率分析仪Zimmer LMG500获得。

图13 功率测试平台

为了对比MEPT算法的控制效果，引入对定磁链下电动机效率的对比分析，两组实验分别运行于500、1 000及1 400 r/min转速下，实验结果如图14所示。因直流源电压等级的限制，在额定转速为1 400 r/min时不能达到额定输出转矩。

图14 不同转速及转矩下的实验结果

由图可知，实验结果与前文的理论分析相吻合，使用MEPT控制可以有效提高电动机的运行效率，在轻载工况下尤为显著。但电动机效率的实测值略低于理论计算值，原因在于损耗模型没有计入机械损耗、杂散负载损耗等。

6 结 语

本文研究了一种针对异步电动机的最大效率转矩比控制算法。为了保证控制算法良好的鲁棒性和动态性能，选取定子磁链为控制对象；同时为了提高效率控制精度，算法依赖电动机效率及损耗模型。本文建立了一套完整的在线效率优化体系，从理论上分析了最大效率转矩比的可行性。为了便于工程应用以及实验分析，依托在线计算建立了离线表。

实验结果表明，在异步电动机全速域额定转矩下运行时所提算法相比于定磁链算法可以明显提高电动机效率，且在轻载时效率提升更加显著。因此对于长时轻载或频繁变载场合，应用此控制策略可实现节能的目的。

[1] Melfi M J, Evon S, Mcelveen R. Induction versus permanent magnet motors[J]. IEEE Industry Applications Magazine, 2009, 15(6):28-35.

[2] 张 奇, 李 珂, 张承慧, 等. 电动汽车用永磁同步电动机特性试验设计与研究[J]. 实验室研究与探索, 2015, 34(10):47-50, 58.

[3] 刘和平, 谭天诚, 郭 强. 一种电动汽车用异步电动机控制策略[J]. 电力电子技术, 2013, 47(9):72-74.

[4] Boldea I, Tutelea L N, Parsa L,etal. Automotive electric propulsion systems with reduced or no permanent magnets: An overview[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10):5696-5711.

[5] Goto S, Hirotsuka I, Nakamura M,etal. Experimental study of losses during high-speed constant-voltage operation of three-phase squirrel-cage induction motors[C]//17th International Conference on Electrical Machines and Systems. IEEE, 2014: 85-88.

[6] 王玉彬, 马文忠. 异步电动机动态节能综合实验平台研制[J]. 实验技术与管理, 2016, 33(6):77-81.

[7] Abrahamsen F, Blaabjerg F, Pedersen J K,etal. Efficiency-optimized control of medium-size induction motor drives[J]. IEEE Transactions on Industry Applications, 2001, 37(6):1761-1767.

[8] Abrahamsen F, Blaabjerg F, Pedersen J K,etal. On the energy optimized control of standard and high-efficiency induction motors in CT and HVAC applications[J]. IEEE Transactions on Industry Applications, 1998, 34(4):822-831.

[9] Wasynczuk O, Sudhoff S D, Corzine K A,etal. A maximum torque per ampere control strategy for induction motor drives[J]. IEEE Transactions on Energy Conversion, 1998, 13(2):163-169.

[10] Kirschen D S, Novotny D W, Lipo T A. Optimal efficiency control of an induction motor drive[J]. IEEE Transactions on Energy Conversion, 1987, 2(1):70-76.

[11] 林友杰, 谢卫才, 吴汉光. 基于功率匹配的异步电动机最大效率控制[J]. 电动机与控制应用, 2009, 36(10):51-54.

[12] 陈 可, 杨文焕. 异步电动机基于在线效率优化的模糊控制[J]. 电动机与控制应用, 2010, 37(12):38-42.

[13] Ebrahim O S, Badr M A, Elgendy A S,etal. ANN-based optimal energy control of induction motor drive in pumping applications[J]. IEEE transactions on Energy Conversion, 2010, 25(3):652-660.

[14] Yu J, Pei W, Zhang C. A loss-minimization port-controlled Hamilton scheme of induction motor for electric vehicles[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(6):2645-2653.

[15] Pyrhonen J, Jokinen T, Hrabovcová V. Design of rotating electrical machines[M]. Hoboken, NJ, USA: John Wiley & Sons, 2009.

MaximumEfficiencyperTorqueControlofInductionMotor

WANGYan,ZHAOHuanli

(School of Electrical and Mechanical Engineering, Pingdingshan University, Pingdingshan 467000, Henan, China)

Aiming at the problem that the direct torque and direct flux linkage control of traditional induction motor do not consider the efficiency of motor, a maximum efficiency ratio control method of asynchronous motor is proposed. This method uses the stator flux linkage as the control object, and gives the flux linkage online calculation method by combining the motor loss model. The online flux linkage calculation is based on the real-time operating conditions of the motor to give the optimal flux linkage reference. The reference is based on the maximum efficiency under current torque, so the proposed method can be applied to direct torque or direct flux control system. Because the motor loss model is dependent on the parameters, and the online calculation is not suitable for industrial applications, a set of off-line tables under different loads at different temperatures are established by the experimental method. The experimental results show that the proposed algorithm is feasible, especially at light load conditions.

induction motor; maximum efficiency per torque control; stator flux; direct flux control

TM 301.2

A

1006-7167(2017)09-0037-05

2016-12-01

河南省科技厅重点科技攻关计划项目(132102110173)

王 艳(1985-)，女，河南平顶山人，硕士，助教，研究方向为电动机控制、电力电子。Tel.：15937506500；E-mail：wangyann1985@163.com