石油钻进过程最优控制

任 伟

（中海油田服务股份有限公司，天津 300452）

石油钻进过程最优控制

任 伟

（中海油田服务股份有限公司，天津 300452）

石油钻进作为探测石油后一个流程，在石油开采中是一个很重要的程序，因此对石油钻进的过程进行研究、分析有着重要的意义。通过阐述在石油钻进的过程中钻进参数在这个过程中所发挥的作用，提出了一种新型的钻探成本计算模型，并用严密的数学公式进行参数的验证，验证我们所进行的计算存在最优值，然后得出最优控制值的分布，使石油钻进施工的成本最小化成为了可能。所提出的最优控制计算模型，对于钻井的流程给予详尽的描述，在仿真实验室里进行验算与实施，保证了其数据的可靠性。

石油钻井；参数；运算；最优化

在进行石油钻井过程模型计算时，利用现有的数据参数进行模型的构建。钻进过程中要保持原有的地质参数不变，使钻井的成本最小化。实际的操作过程是从钻头钻入到地下然后达到地层，在这个过程，其他的外界参数都不改变，保持钻头的转速与压力，最终实现钻井成本的最小化。

1 钻井实际中遇到的问题

当实际进行钻井施工时，进行优化控制时，很多因素都要考虑，比如：随着钻头深入的地面层次不一样，钻头的摩擦受损程度也不一样。但是这些因素都在所建的参数模型中被考虑。然而钻井技术的提升，也产生了新的问题：第一，成本模型函数是以单个钻头钻井的成本与钻入的尺度的函数，是一个均衡的概念，计算的方式比较简单，钻井越深，计算出的成本误差越大；第二，更加高效的钻头，一个钻头可以钻到百米内，也能钻到千米之外，这是就需要考虑地下的地质参数；第三，当钻头使用时间长时，就出现磨损，钻头的螺纹和刀口都磨损严重，可能导致施工的时候出现安全问题。

对上面的出现的问题，提出了新的计算方式，即保持单位尺度的成本最小，然后保持整个钻井过程的总费用是最低的，在这个因素下，研究出最优的数据去保持成本的最小化。问题就变成计算最优参数的数学题。

2 系统方程状态

2.1 系统的方程

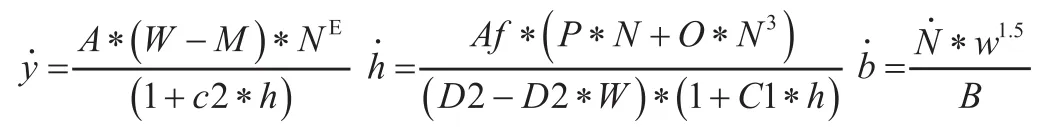
2.2 系统状态

初态终态控制变量 W（t）、N（t）。

状态变量 y（t）、b（t）、h（t）。

2.3 目标函数

从以下的函数中二选一，第一，瞬间尺度成本，改变传统的平均单位成本，改为尺度单位成本；第二，尺度总成本，由瞬间单位成本与其他参数。

2.4 单位成本与总成本

以钻头的磨损量h、轴承磨损量b、时间段t为参数构建函数关系进行瞬时单位成本C的计算。根据微分函数在每一个瞬时阶段花费的各种费用的总和，可以进行瞬时总成本dc函数方程的构建：dc=dcb+dcx+Crdt，通过微总成本，可以计算出整个过程的总成本。

3 形成控制模型

根据前面的研究，瞬间单位尺度成本的最小化为最优成本，这个计量标注更为精确，比平均单位尺度成本更低。

3.1 简化状态

为了把数据进行简单量化，确定终端数据为定值，是可以控制的一个最优值。为了获得最优成本，应花费更少的时间进行钻井活动，能起到降低成本的作用。

3.2 进尺状态量的确定

为了更好地展示瞬时尺度成本的最优值是低于平均成本的最优值，可以把模型中的y值取均值的最小值，用瞬时成本的最优值作为参数，进行钻井成本的计算。

4 控制参数的计算

4.1 地质参数不变

假设钻所钻入的尺度，以及该地质层的参数是一样的，即A、Af、M、E等是固定常数，不因为其他的外界因素变化而变化。我们在认定瞬时尺度成本为Z时，参数之间是微积分函数关系，因此当条件给定时，按照上文设定的数学公式模型，利用数学微积分运算法则，带入模型参数、数据进行计算，就能得到最优控制的成本。

4.2 地质参数变化

实际情况中，地质层的参数随着深度的不断加深，参数也在不断变化。因此在进行实际计算时，要考虑到这些因素，运用数学模型进行计算时要灵活。当地质参数变化不频繁时，运用定值参数的模型进行成本的最小计算，如果参数变化较大，可以进行阶段划分，划分为多个小阶段进行计算，计算出最小的可控成本。

5 实际计算

根据参考文献[1]中参数数据进行模拟计算最优成本，其中的时间间隔以半个小时为尺度，进行对照实验，根据模型可以计算出控制曲线、钻速曲线等曲线。具体见图1。

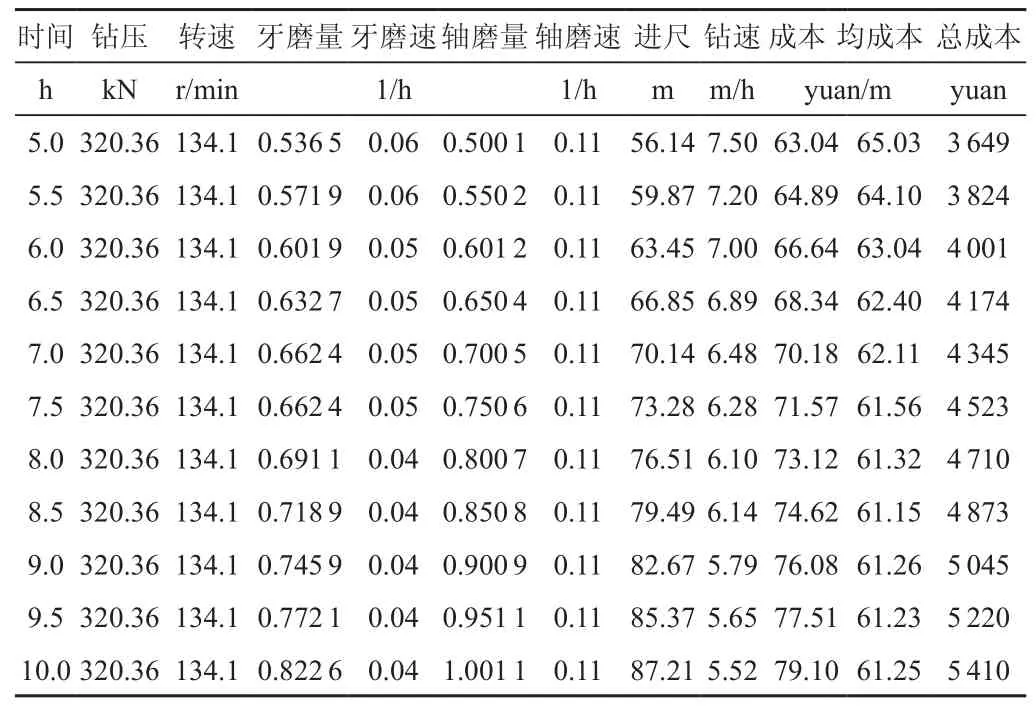
表1 最优控制参数值表

5.1 控制曲线分析

根据我们所做的图表得出的数据可以看出，在以0.5h为尺度的分段中，保持牙磨速不变的情况下，钻压基本曲线接近水平线，在尺度与尺度之间的变化波动几乎不明显；钻头的钻速却在一直增大，相应的磨损量与磨损速度都在不断增加，保持线性增长；平均成本保持随着时间段的增加而不断降低，但是瞬时成本却在不断提升。

5.2 成本曲线

瞬时单位成本随时间递增也逐渐增加，平均单位成本却呈递减状态，总成本必然是不断增加的。

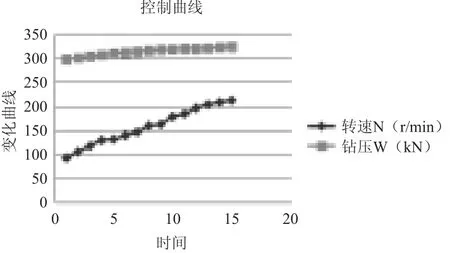
图1 控制曲线图

6 结束语

我们在进行最优成本计算时，通过计算瞬时成本的最优控制得出最优总成本的控制模型。通过利用求极小值的一些必要条件公式进行参数计算，我们得出对于参数一直变化成本控制比不变参数的成本控制更好，单位成本的计算方法可以用在变参与定参之间的任何一个模型之中。通过我们的最优成本的控制模型计算，为我们以后石油钻探成本降低提供了依据。

[1] 王子健，申瑞臣，王开龙，等.基于最优控制理论的智能井动态优化技术[J].石油学报，2012，33（5）：887-891.

[2] 张慧平，王建民.最优控制技术在现代过程工业中的应用与展望[J].北京石油化工学院学报，2013，21（4）：62-66.

Optimal Control of Oil Drilling Process

Ren Wei

Petroleum drilling，as a process of detecting oil，is a very important procedure in petroleum extraction.Therefore，it is of great significance to study and analyze the process of oil drilling.This paper describes the role of drilling parameters in the process of oil drilling.Put forward a new kind of drilling cost calculation model，and the parameters were verified by mathematical formulae strict，verified the existence of the optimal value，then draw the distribution of optimal control value，so that the oil may be the drilling cost minimization of construction.The optimal control model proposed in this paper gives a detailed description of the drilling process，and checks and implements it in the simulation laboratory，thus ensuring the reliability of the data.

oil drilling；parameter；operation；optimization

TE2

A

1003–6490（2017）10–0233–02

2017–07–16

任伟（1985—），男，辽宁阜新人，助理工程师，主要研究方向为浅层石油定向井钻井工艺、跟套管钻进技术等。