可预测弹道目标的鱼雷射击参数计算方法

李长文,初 磊,毛俊超

(海军潜艇学院,山东 青岛,266199)

可预测弹道目标的鱼雷射击参数计算方法

李长文,初 磊,毛俊超

(海军潜艇学院,山东 青岛,266199)

为解决对非等速直航目标的鱼雷射击参数计算问题,研究了对可预测弹道目标射击参数计算的一般方法。对鱼雷弹道以分段增量的形式进行了表达,给出了射击参数计算模型,与对等速度直航目标射击的主要不同是需要解一个二元非线性方程组。针对理想声自导运动目标,以微分方程数值解计算预测的目标状态,用Newton迭代计算二元方程组的数值解。数值试验发现,这一方法能快速准确地计算出射击参数,可为解决鱼雷对非等速直航目标的射击参数计算问题提供参考。

鱼雷; 射击参数; 可预测弹道目标

0 引言

对目标进行鱼雷攻击之前,需要装订计算的射击参数。射击参数与所侦测的目标信息、选用的鱼雷使用方式等有关,目标信息包括目标性质、相对本平台的态势、运动状态等; 鱼雷使用方式包括直航、自导和线导等。

攻击平台可以是潜艇或水面舰船,被攻击目标可以是潜艇或水面舰船,还可以是鱼雷或诱饵等其他水面或水下航行的小目标。还有一个特例,就是以鱼雷攻击鱼雷,攻击方的鱼雷一般称为反鱼雷鱼雷。

射击参数的计算,是为了达成特定的目的,这个特定目的一般可用假设无误差条件下遮盖中心与瞄准点以预定的相遇态势重合进行表达[1]。在采用估计的目标运动要素条件下,对于等速直航目标,由于目标航向与时间无关,射击参数计算的关键为解一个一元方程[2],已经有标准的方法解决这一问题。反鱼雷鱼雷的攻击对象不一定是等速度直航目标,这需要与之不同的射击参数计算方法,但相关的文献[3-9]未发现这方面的报导,文中试图探讨一般方法,对假设目标为理想声自导鱼雷情形进行初步研究。

1 一般方法

1.1 基本假设与记号

假设攻击平台与目标的运动可视为同一水平面上的运动,以tp表示攻击平台对目标运动要素解算的结束时刻,即采用目标运动要素时刻。以tp时刻本平台对目标的观测基准点为原点,正北方向为xv轴正方向,正东方向为yv轴正方向建立一个水平面上的直角坐标系,平台、目标和鱼雷等物体的运动状态以速率,航向,位置表示。

攻击平台的运动状态记为

对于平台一方,p（t）可视为已知。

目标的运动状态记为

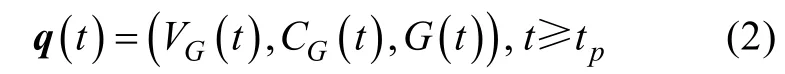
q（tp）为计算射击参数所采用的目标运动要素。

所谓可预测弹道,规定为不考虑观测误差条件下,t≥tp时刻的弹道状态可表示为tp时刻的目标运动要素q（tp）及当前时刻之前的平台运动状态（p（u）,tp≤u≤t）的确定函数,即

假设理想声自导运动的目标速率不变,航向为目标到平台的方向,则且

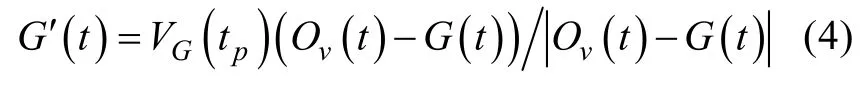
该微分方程的初值问题有唯一解,且与tp时刻的航向无关,只与和q（u）,(tp≤u≤t)有关。因此,理想声自导运动目标的弹道为可预测的。

理论上,只有可预测弹道的目标,其运动要素才能用一些含随机误差的观测进行解算,对等速直航目标运动要素的解算是一个比较经典的问题,对假设以理想声自导方式运动目标的运动要素的解算,公开报导可见[10],此处不涉及这一问题。假设目标运动要素已给出,平台对目标的射击是自时刻tp算起,经时间延迟dτ后于tl=tp+τd时刻发射鱼雷,其弹道状态记为如图1所示,假设鱼雷发射后的弹道阶段为: 1) 确定的初始弹道:一次转角3) 一次转角后直航,二次转角确定的自适应等特殊弹道,6) 确定的部分直航搜索弹道,E⇒A（t）,其中确定弹道的参数是已知的或可预先设定的。各弹道阶段所用时间以τj表示,则各弹道阶段的结束时刻为结束时刻与开始时刻速率、航向、位置之差(以下称之为各弹道阶段的速率、航向、位置增量)各记为ΔVAj,ΔCAj和ΔAj。则各阶段开始时刻的速率、航向和位置为

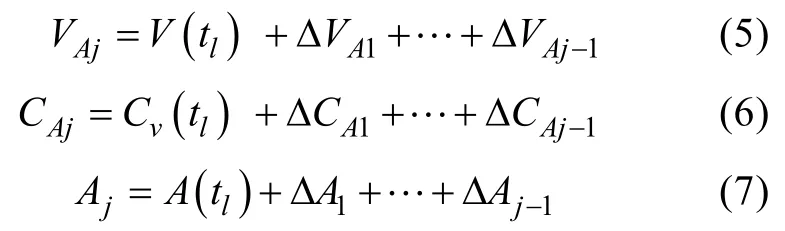
其中,jτ,ΔVAj,ΔCAj,ΔAj由各弹道阶段的实际变速、变深和变向等逻辑决定,若无变向,则若无变速,则对于转角的运动,假设转角运动为角速率Aω的匀速圆周运动,则转角所用时间为速率增量为0,航向增量为,位置增量为

其中,CA为开始时刻的航向。利用这些公式可以计算各阶段的增量,确定的弹道阶段所用时间为已知。

图1 射击参数计算原理图Fig. 1 Principle of computing shooting parameter

瞄准点为与目标固连的动点Tp,其相对目标的距离和舷角记为遮盖中心为与鱼雷固连的动点Ap,其相对鱼雷的距离和舷角记为。所谓预定相遇态势,是指无误差条件下,于一定时刻t,Ap与Tp重合,且目标航向相对鱼雷航向的反方向的角等于预先设定的通常设置对于不预设相遇态势的情形,以表示,对应

1.2 射击参数满足的方程

为简单起见,假设鱼雷的所有变速、变深运动已于弹道阶段 1)完成,利用以上假设及记号,射击参数满足方程组

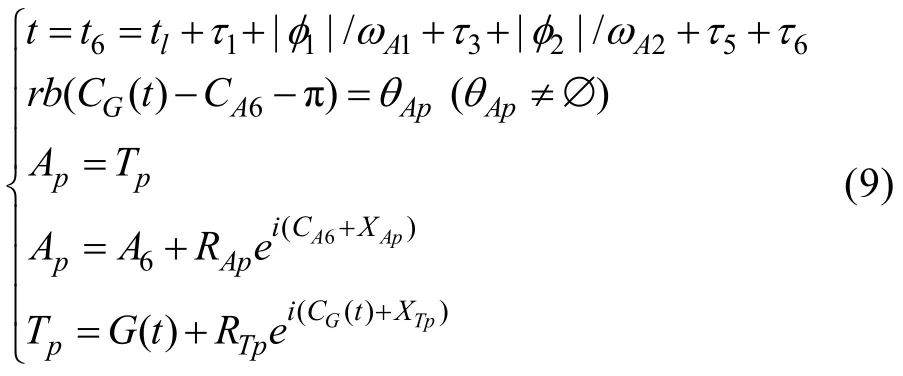
其中,rb（x）表示将任意角x变为[-π,π)上与之终边相同角的函数。

令τ=t-tl,即自鱼雷发射至遮盖中心与瞄准点重合的时间,则且一次转角完成至二次转角开始时刻的时间为其中和为一、二次转角运动的角速率。

这个函数关于1φ,的偏导数为

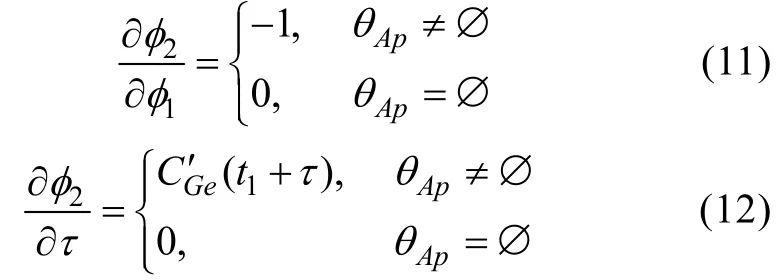
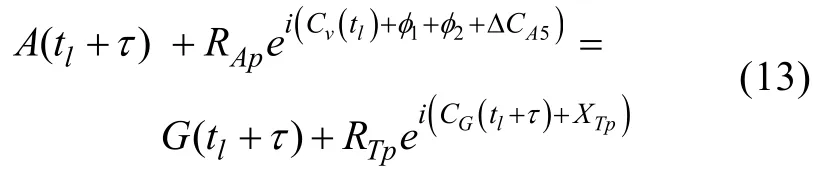
确定,其中

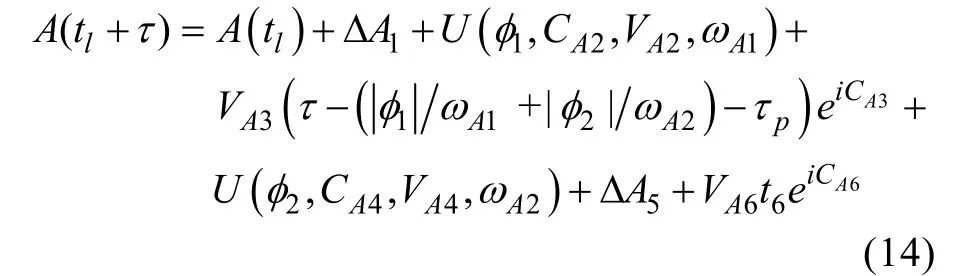
为τ的线性函数。

1.3 射击参数的一般算法

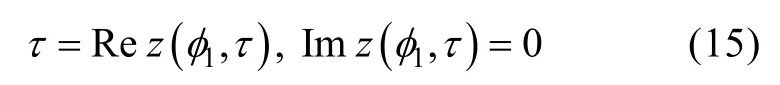
若此方程组的解不唯一,可取对应的τ最小的那一组,考虑到限制则应为

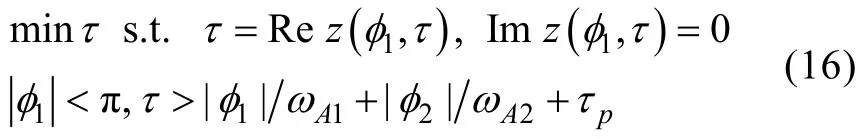
与针对等速直航目标计算射击参数的关键是解一个一元方程不同,上述优化解法的关键是解一个二元方程组,为此,记

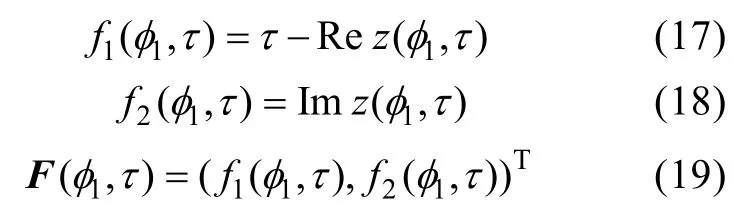
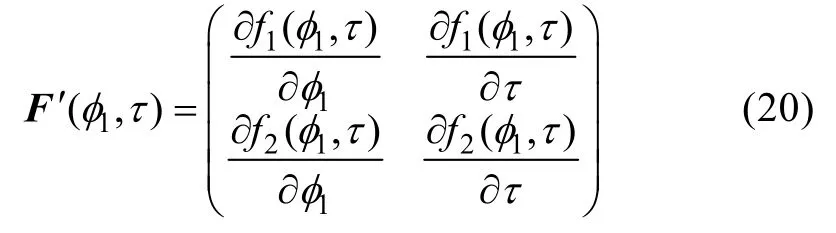
利用这些求导运算与复数取实部或虚部运算可交换的性质,可以方便地给出上述各导数的解析公式,对φ1的求导运算需要利用等公式,对的求导运算可利用

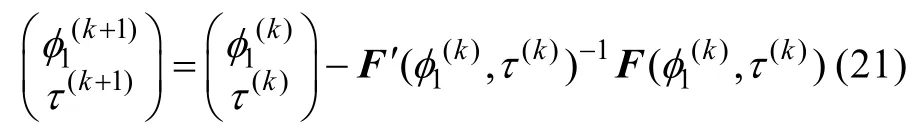
2 理想声自导目标的射击参数计算

对于平台作等速直航运动的情形,上述微分方程有隐式解析解,可以用解一个代数方程的方法计算预测的弹道状态,也可以用解析公式计算,这种方法可以认为是精确计算,且计算速度快,在计算理想声自导鱼雷状态、解算声自导鱼雷运动要素等方面使用这一方法[10]。为了验证上述方法的可用性,此处考虑一般情形,以这个微分方程的数值解预测其弹道状态,同时以数值导数计算用于计算Newton叠代的Jacobi矩阵。

为了验证上述方法的正确性,随机选取XAp、其他参数在容许范围内选取,数值试验发现,上述方法总能快速计算出射击参数或判定无解。有解的情形,Newton 叠代次数一般5次左右。

图2为一次计算的函数g(φ1,τ)的等值线图,图3为相应的运动图。

图2 函数 g(φ1,τ )的等值线图Fig. 2 Contour of function g(φ1,τ )

3 结束语

文中将鱼雷射击参数计算抽象为可预测弹道目标的射击参数计算问题,主要是为了拓宽射击参数计算范围至非等速直航目标情形,所建立的射击参数计算模型满足二次转角射击弹道及预定相遇态势要求,模型求解的关键是解一个二元非线性方程,可用比较标准的方法实现。用假设的理想声自导运动目标对这一方法进行了验证,仿真试验发现,可用不太复杂的方法实现这一目的,计算速度及稳定性等可满足实时计算的需要。

图3 一次计算的运动图Fig. 3 Motion graph of once computation

由于这方面的知识未发现公开报导,本文研究仅为初步,理论与方法有待进一步质疑。

[1] 李本昌,李长文. 预定相遇态势的潜射鱼雷射击及其技术方法[J]. 指挥控制与仿真,2013,35(2): 5-8.Li Ben-chang,Li Chang-wen. Firing and Technical Model Based on Given Meeting Situation of Sub-launched Torpedo[J]. Command Control & Simulation,2012,34(5):94-98.

[2] 李长文,李本昌,初磊. 预定相遇态势的鱼雷二次转角射击通用模型与算法[J]. 鱼雷技术,2013,21(4): 306-312.Li Chang-wen,Li Ben-chang,Chu Lei. General Model and Algorithm of Two-time Turn Angle Shooting of Torpedo for Predetermined Encountering Situation[J]. Torpedo Technology,2013,21(4): 306-312.

[3] 崔贵平. 国外反鱼雷鱼雷技术发展及趋势[J]. 舰船科学与技术,2013,35(3): 138-141.Cui Gui-ping. Foreign Anti-Torpedo Torpedo Development and Trend Analysis[J]. Ship Science and Technology,2013,35(3): 138-141.

[4] 由大德,徐德民. 反鱼雷鱼雷拦截概率影响因素仿真分析[J]. 鱼雷技术,2010,18(4): 312-315.You Da-de,Xu De-min. Analysis on Parameters Influencing Intercept Probability of Anti-torpedo Torpedo[J]. Torpedo Technology,2010,18(4): 312-315.

[5] 范路,吕瑞,王志杰,等. 反鱼雷鱼雷自导导引弹道方法研究[J]. 舰船电子工程,2014,34(3): 162-164.Fan Lu,Lü Rui,Wang Zhi-jie,et al. Homing Model of Torpedo and the Usual Homing Model of Anti-torpedo Torpedo[J]. Ship Electronic Engineering,2014,34(3):162-164.

[6] 范路,王志杰,曹小娟. 反鱼雷鱼雷拦截弹道导引方法研究[J]. 舰船科学技术,2014,36(2): 77-81.Fan Lu,Wang Zhi-Jie,Cao Xiao-juan. Research on the Usual Homing Model of Anti-torpedo Torpedo[J]. Ship Science and Technology,2014,34(3): 162-164.

[7] 夏睿,张静远,张江,等. 反鱼雷鱼雷初始占位搜索研究[J]. 船电技术,2013,33(1): 22-24.Xia Rui,Zhang Jing-yuan,Zhang Jiang,et al. Research on the Anti-torpedo Torpedo Initial Search Sites[J]. Marine Electric & Electronic Engineering,2013,33(1): 22-24.

[8] 李宗吉,张西勇,练永庆. 基于变结构控制的反鱼雷鱼雷导引律鲁棒性研究[J]. 鱼雷技术,2014,22(4): 272-276.Li Zong-ji,Zhang Xi-yong,Lian Yong-qing. Robustness of Anti-Torpedo Torpedo Guidance Law Based on Variable Structure Control[J]. Torpedo Technology,2014,22(4):272-276.

[9] 刘洋,李宗吉,张西勇. 基于变结构控制的反鱼雷鱼雷导引律设计[J]. 鱼雷技术,2013,21(1): 39-42.Liu Yang,Li Zong-ji,Zhang Xi-yong. Design of Guidance Law for Anti-torpedo Torpedo Based on Variable Structure Control[J]. Torpedo Technology,2013,21(1): 39-42.

[10] 李长文,初磊. 理想声自导运动要素的距离方位观测解算方法[J]. 弹道学报,2016,21(3): 43-47.Li Chang-wen,Chu Lei. Method on Solving Ideal Sound Self-guided Torpedo Motion Factors by Distance and Bearing Observations[J]. Journal of Ballistics,2016,21(3):43-47.

Computation of Torpedo Shooting Parameter for Target with Predictable Trajectory

LI Chang-wen,CHULei,MAOJun-chao
(Nary Submarine Academy,Qingdao 266199,China)

To compute torpedo shooting parameters for a straight running target with non-constant velocity,a general method for computing torpedo shooting parameter for a target with predictable trajectory is presented. For easy understanding and application,the torpedo trajectory is expressed in form of subsection increment,and a computation model of shooting parameter is established. Compared with the method for shooting a target with constant velocity,the proposed method needs to solve a system of nonlinear equations with two unknowns. For an ideal acoustic homing target,the numerical solution of a differential equation is used to compute the target state,and Newton iteration is adopted to compute the numerical solution of the system of binary equations. Numerical experiment indicates that this method can compute shooting parameter rapidly and accurately.

torpedo; shooting parameter; target with predictable trajectory

TJ630; TB112

A

2096-3920(2017)03-0267-05

李长文,初磊,毛俊超. 可预测弹道目标的鱼雷射击参数计算方法[J]. 水下无人系统学报,2017,25(3): 267-271.

10.11993/j.issn.2096-3920.2017.03.009

2017-03-31;

2017-04-16.

李长文(1962-),男,硕士,副教授,主要研究方向为应用数学.

(责任编辑: 陈 曦)