基于跳数分类的改进DV-Hop节点定位算法

2017-11-03任克强廖美焱

传感技术学报 2017年10期

关键词：跳数信标半径

任克强,廖美焱

(江西理工大学信息工程学院,江西赣州 341000)

2017-03-28修改日期2017-06-07

基于跳数分类的改进DV-Hop节点定位算法

任克强*,廖美焱

(江西理工大学信息工程学院,江西赣州 341000)

在传统DV-Hop节点定位算法中,不同的网络节点密度使得节点之间不同跳数的平均每跳距离差异较大,跳数越多误差越大。为了减小平均每跳距离差异对节点定位精度的影响,提出一种DV-Hop改进算法。改进算法首先提出跳数分类的策略对网络中不同的跳数进行分类,以减小不同跳数之间平均每跳距离差异的影响,提高节点的定位精度;然后对加权最小二乘估计进行改进,采用改进的权系数取值策略来适应累积误差的非线性变化,从而更好地控制不同跳数在最小二乘估计中的权重,以减小因跳数增加而产生的累积误差,进一步提高节点的定位精度。实验结果表明,改进算法可以有效地减小平均每跳距离差异以及高跳数对节点定位的影响,节点定位性能显著优于传统DV-Hop节点定位算法,相较于对比文献也有一定的提升,并且对不同的网络节点密度具有更好的适应性。

无线传感器网络;节点定位;DV-Hop算法;跳数分类;加权最小二乘估计

计算机和传感器技术的迅速发展使得无线传感器网络WSN(Wireless Sensor Network)获得了广泛应用和关注。WSN是由许多能量有限、低成本和低功耗的传感器节点通过自组织多跳形成的网络系统。每个传感器节点都配备了传感元件、数据处理单元、无线接收发器模块和电源模块,具有信息采集、数据处理和通信的能力,但是这种计算和通信能力是有限的[1]。在WSN中,对每个传感器节点进行定位十分重要,如果传感器采集的数据没有空间和时间的协调,那么采集的数据将没有价值[2]。

WSN的定位技术根据测距方式可以分为基于测距(range-based)的定位和非测距(range-free)的定位两大类[3-4]。其中,基于测距的方案需要有精确测量两相邻节点间的绝对距离或者方位的有关设备,导致基于测距的方案对硬件设备要求较高,但是定位的精度相对非测距要高。基于测距的定位算法主要包括:TOA、TDOA、AOA和RSSI等[5-6]。在非测距的方案中,存在两种节点,一种是位置已知的信标节点(anchors nodes),另外一种是未知节点(unknown nodes),非测距主要是利用已知节点估计未知节点的位置。因而,非测距方案不需要额外设备,适合在大规模的传感器网络中部署,其最大缺点就是误差较大。典型的非测距定位算法主要有:Centroid[7]、DV-Hop[8]、Amorphous[9]以及APIT[10]等。

DV-Hop算法是一种典型的基于跳数的非测距定位算法,协议简单且方案易部署,受到了广泛的关注与研究,但其定位性能不理想。在DV-Hop算法的基础上,许多学者提出了改进算法。文献[11]对算法的改进集中在计算每跳距离,提出对全网络信标节点的平均每跳距离相加求平均,得到全网络的平均每跳距离,并用2-D双曲线(hyperbolic)代替最大相似(maximum likelihood)估计未知节点坐标,取得了一定的效果,但该算法在网络密度较低时误差较大。文献[12]提出一种基于误差距离加权与跳数算法选择的遗传优化DV-Hop定位算法,该算法以距未知节点越近越重要为原则,对信标节点进行挑选并优化,从而减小定位误差。文献[13]将跳数进行量化,并将通信半径长度量化为多跳,最后采用自适应质点弹簧优化算法优化节点坐标,提高了定位精度,但该算法需要额外测距技术获得距离信息,增加了部署成本。文献[14]提出基于SFLA(shuffled frog leaping algorithm)和PSO(particle swarm optimization)的定位算法,SFLA用来计算平均每跳距离,PSO用来计算未知节点坐标,取得了较高的定位精度。文献[15]主要针对DV-Hop算法的第3步进行了改进,使其具有更小的校正因子,并通过加权最小二乘估计未知节点坐标,算法性能比DV-Hop算法有较大提升。上述算法均不同程度的改善和提升了DV-Hop算法的性能,但这些算法只是利用节点的联通度或跳数信息进行定位,并未考虑到网络节点密度的改变对节点之间不同跳数的平均每跳距离的影响。因此,本文提出一种跳数分类与改进加权最小二乘估计相结合的DV-Hop改进算法,以减小网络密度变化和累积误差对节点定位的影响,提高DV-Hop算法的定位性能。

1 DV-Hop算法及其误差分析

1.1 DV-Hop算法

在DV-Hop算法的距离向量定位机制中,节点主要是利用节点之间的信息交换来对自身的位置进行估计,主要包括下述3个步骤:

①所有信标节点先创建一个初始化的信息分组表{xi,yi,hi},其中包括自身坐标{xi,yi}和初始跳数hi=1,并向邻居节点广播自身信息分组;由于节点发射功率的限制,只有位于节点传播范围内的邻居节点(neighbor node)才能接收到该数据包。邻居节点接收到这些数据包后,如果该数据包是来自同一信标节点的跳数较大的信息分组,则抛弃该数据包,否则将其记录下来,再将信息分组表内的hi加1后转发。

②通过步骤1中节点之间的信息分组表交换,所有网络当中的未知节点都可以知晓自身到信标节点的最小跳数和信标节点的信息,如坐标和编号。相应的,信标节点之间也获得了彼此之间的最小跳数和坐标信息。然后,信标节点可计算出自己到其他信标节点的平均每跳距离:

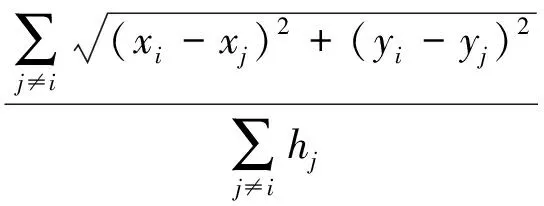
(1)

式中:{xi,yi}和{xj,yj}分别表示信标节点i和j的坐标,hj表示信标节点i与j之间的最小跳数。

信标节点计算出平均每跳距离HopSizei后,将各自的平均每跳距离广播给邻居节点。未知节点通过第2次的信息交换可获知离自己最近信标节点的平均每跳距离。

③未知节点获得离自己最近信标节点的平均每跳距离后,根据式(2)计算到各信标节点的距离Dis(i,j):

Dis(i,j)=hij×HopSizej

(2)

式中:hij表示未知节点i到信标节点j的最小跳数,HopSizej表示离未知节点i最近信标节点的平均每跳距离。

最后利用三边测量法或者极大似然估计法估计未知节点的坐标。

1.2 算法误差分析

图1中分布着两个信标节点S和D以及若干个未知节点。

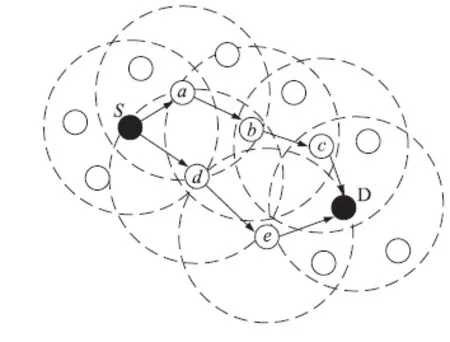
图1 节点分布示意图

从图1中可以得出以下两个结论:

①DV-Hop算法计算出的平均每跳距离HopSizei必小于等于实际的平均每跳距离。该结论是显然的,由于两点间的直线距离最短,采用多跳所走过的路径必然大于等于直线间的距离。

②在两个固定距离的信标节点之间,跳数越多,单跳距离越小。例如:节点S到节点D可以通过S→a→b→c→D,也可以通过S→d→e→D,显然两种多跳方式所计算的平均每跳距离不相等。

DV-Hop的主要思想是未知节点利用信标节点所计算出的平均每跳距离来估计自己到信标节点的距离,这种估计是采用折线去估计直线距离,但是这个折线距离并不等于真实的折线距离,它比真实的折线距离要小,这对估算直线距离是有利的,结论1说明了这一点。结论2主要说明了网络节点密度的差异容易导致不同跳数所计算的平均跳距差异很大。因此,在网络拓扑结构分布不规则的情况下,采用式(1)或者文献[11]全网络平均算法的误差会很大。

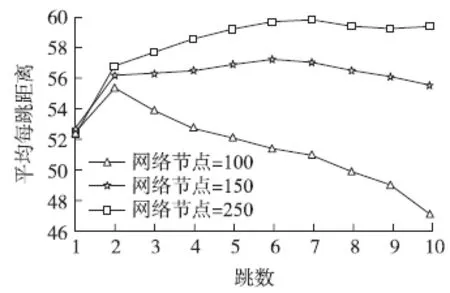
图2 不同跳数的平均每跳距离

为了更深入的研究不同跳数所计算的平均每跳距离的变化规律,本文做了如下仿真实验:在500 m×500 m的区域内分别随机分布100、150和250个节点,其中信标节点40个,通信半径R=80 m,分别分类计算信标节点之间不同跳数的平均每跳距离,实验结果如图2所示。

从图2中可以看出平均每跳距离随网络节点密度的3个变化规律:

①信标节点之间不同跳数计算出来的平均每跳距离差异较大。

②从横坐标看,3种不同节点分布密度呈现出3种不同的变化规律,当网络节点个数为250时,随着跳数的增加,平均每跳距离呈现逐渐上升,最后趋于平稳;当网络节点个数为150个时,随着跳数的增加,平均每跳距离先呈现出上升,最后呈现出下降的趋势;当网络节点个数为100个时,随着跳数的增加,平均每跳距离逐渐下降。

③从纵坐标看,当跳数固定时,随着网络节点数的减少,平均每跳距离逐渐减小。

上述3组实验分别代表着3种节点密度,250代表节点密度较高,150代表节点密度中等,100代表节点密度较低。当网络中节点密度较高时,节点分布较为均匀,随着跳数的增加,平均每跳距离趋于平稳;当网络中节点密度较低时,节点分布不规则,在相同距离的两信标节点中间,容易出现较为曲折的折线,导致跳数的增加,从而平均每跳距离减小。

因此,在网络节点密度较低或者网络拓扑分布不规则时,采用DV-hop算法或全网络平均算法是不可取的,误差会很大。此外,文献[16]的分析表明随着未知节点到信标节点跳数的增加,未知节点到信标节点的估计距离误差将会逐渐增加。

2 改进策略

2.1 跳数分类策略

根据上述误差分析,在网络拓扑结构不规则时,不同跳数所计算出的平均每跳距离差别较大,而且这种差别会随着网络节点密度的不同而不同。因此本文提出一种跳数分类HCC(Hop Counts Classification)的改进策略,以减小不同跳数之间平均每跳距离的差异,提高节点的定位精度。

设网络中有n个节点,其中有m个信标节点,信标节点之间的欧氏距离为:

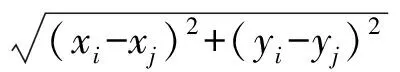
(3)

式中:{xi,yi}和{xj,yj}分别表示信标节点i和j的坐标。

HCC策略共由3个阶段组成:

①节点初始化。数据包先从信标节点进行广播。每一个信标节点向邻居节点广播一个初始化信息Info=[(Bi,xi,yi),HopCouti],其中Bi表示信标节点编号,{xi,yi}表示信标节点Bi的坐标,HopCouti表示跳数(初始化为1)。由于节点发射功率的限制,只有位于节点传播范围内的节点才能接收到该数据包,即与信标节点之间为一跳的节点都可以接收到该数据包。节点接收到数据包之后,判断该数据包是否来自同一信标节点的跳数较高的信息分组,如果是则抛弃该数据包;否则,更新自身的数据,并将更新的数据包转发。新转发的数据包含有信标节点信息和更新的数据:

(4)

图3 数据包处理伪代码

②信标节点跳数分类。当所有节点获知自身到信标节点的最小跳数之后,所有信标节点将自身的最小跳数集合seti发送到汇聚节点,汇聚节点对所有信标节点的最小跳数集合进行跳数分类。

dperhop(c)=fc(set1,set2,…,setm)

(5)

跳数分类过程如图4所示,x1,x2,…,xm-1,xm分别表示m个信标节点的最小跳数集合,在这些集合当中,都含有该信标节点i与其余信标节点之间最小跳数。然后通过分类器函数fc可以得到一个h维的向量y,向量y中的每个值分别代表不同跳数的平均每跳距离。h的值取决于它们之间的最高跳数。

图4 跳数分类示意图

分类器函数fc的映射过程描述如下:

S1:输入m个信标节点的跳数集合set1,set2,…,setm,setm内包含了信标节点Bm与其余信标节点的最小跳数集合hopm1,hopm2,…,hopmm-1。

S2:对集合内的所有数据进行分类处理,输出h个最小跳数相同的集合Bhop1,Bhop2,…,Bhoph。例如,信标节点B2到B4为3跳,B1到B5也为3跳,则将信标节点之间最小跳数为3跳的组成一个集合Bhop3。

S3:计算不同跳数之间的平均每跳距离:

(6)

式中:M表示集合Bhopc里面的信标节点对数,disij表示集合内信标节点之间的距离,dperhop(c)表示跳数为c跳的平均每跳距离。

S4:计算节点到各信标节点的距离:

Disij=HopCoutij×hopCoutij

(7)

③未知节点坐标估计。为减小误差积累对定位的影响,本文采用改进的加权最小二乘估计对未知节点的坐标进行估计。

2.2 加权最小二乘估计的改进

设网络中信标节点的坐标分别为(x1,y1),(x2,y2),…,(xn,yn),待估算未知节点的坐标为(x,y),待估算未知节点到信标节点i的估计距离为di(i=1,2,…,n),则可得如下方程组:

(8)

将式(8)方程组的前(n-1)个方程分别减去第n个方程可以得到AX=b形式的矩阵,其中,A与b为n-1维观测值,X是未知参数:

(9)

(10)

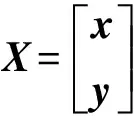
(11)

min(b-AX)T(b-AX)

(12)

对X求偏导数,并令其等于零,可求得X的估计值:

(13)

由文献[16]的分析可知,随着未知节点到信标节点跳数的增加,误差逐渐增加(拓扑是随机分布的,随着跳数增加,各种不确定性因素增多),也就是说误差向量e中的每一个误差可信度会随着跳数的增加而减小。为了减少这种累积误差,可采用加权最小二乘估计代替最小二乘估计:

min[W(b-AX)]T[W(b-AX)]

(14)

式中:W表示权系数,W是一个维数为n-1的对角矩阵。

对X求偏导,并另其等于零,可求得X的加权估计值:

(15)

对于权系数W,文献[15]采用跳数的倒数作为权系数的取值:

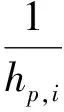
(16)

式中:Wp,i表示未知节点p对于信标节点i的权系数;hp,i表示未知节点p到信标节点i的最小跳数。

文献[15]权系数取值的基本思路是:未知节点p到信标节点i的跳数越多,所对应的权越小。这种权系数的取值策略有效地减少了累积误差,提高了定位精度;但累积误差增加与跳数增加之间的关系不是线性的,该权系数取值策略没有考虑累积误差增加的非线性特点,其权系数取值不是根据累积误差的非线性变化而自适应的确定,不能适应累积误差的非线性变化。因此,为了进一步减少累积误差,本文对权系数的取值进行了改进:

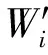
(17)

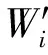
本文的权系数取值策略既考虑了跳数增加导致累积误差非线性逐渐增加的因素,又利用了跳数分类得到的一跳平均距离均方误差最小的特点。表1给出了节点总数为500个、信标节点占15%和通信半径R=70 m时,信标节点之间不同跳数的均方误差,可以看出:一跳的均方误差最小;均方误差随着跳数的增加而逐渐增加,但增加的幅度不是线性的。

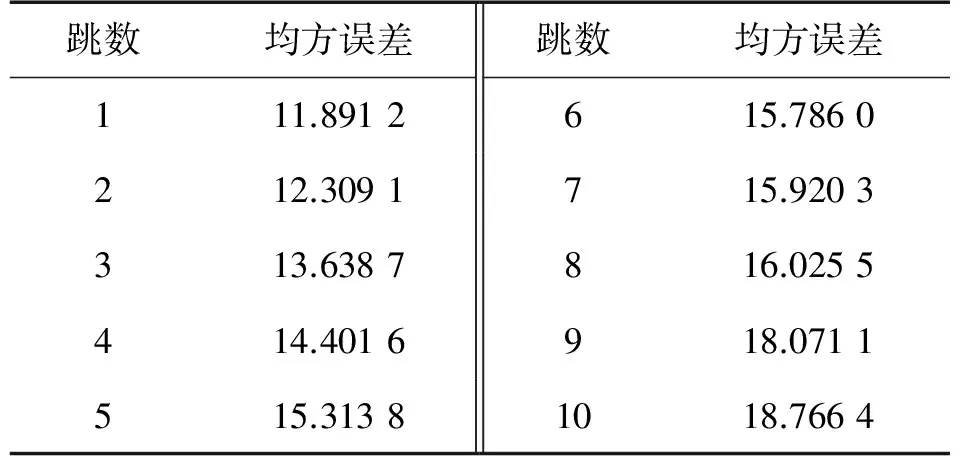
表1 不同跳数的均方误差

3 实验仿真与分析

为了测试本文改进策略的效果,采用MATLAB对DV-Hop算法、文献[15]算法以及本文算法进行仿真实验,并以平均相对误差为标准对仿真结果进行分析评价:

(18)

实验场景为100 m×100 m的矩形区域,仿真实验分成三组,每组的实验结果为分别仿真100次的平均值;通信半径为R,考虑到真实的通信半径并不是标准的圆,允许每个节点的R有0～10%的误差波动。

图5是网络节点个数从200到500变化对定位误差影响的实验结果曲线,其中节点总数的10%为信标节点,通信半径R=15 m。可以看出,随着网络中节点总数的增加,DV-Hop算法、文献[15]算法以及本文算法的相对定位误差都逐渐下降。当节点从200个增加到500个时,DV-Hop算法的相对定位误差为33%,文献[15]算法的相对定位误差为21%,文献[15]算法比DV-Hop算法的相对定位误差减小了12%;本文算法的相对定位误差为20%,进一步减小了定位误差,说明本文算法的定位精度比DV-Hop算法有了大幅的提高,比文献[15]的定位精度也有一定的提升。图5的实验结果曲线表明增加网络中的节点个数可以较为有效的降低定位误差,这是因为节点总数增加,网络节点密度随之增加,在节点的通信半径内,将会出现更多的邻居节点,使得网络拓扑更加规则,而网络拓扑越规则,误差的积累会越小,从而使得定位误差减小。

图5 网络节点个数对定位误差影响

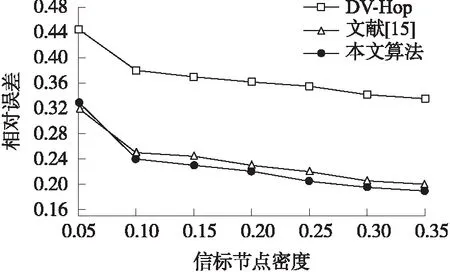
图6 网络信标节点密度对定位误差影响

图6是网络信标节点密度的变化对定位误差影响的实验结果曲线,网络中总共包含有节点300个,信标节点比例从5%到35%变化,通信半径R=15 m。当网络中信标节点比例由5%增加到10%时,3种算法的相对定位误差曲线均下降明显;当网络中信标节点比例由10%增加到30%时,3种算法的相对定位误差曲线下降较为缓慢;当网络中信标节点比例大于30%时,随着信标节点密度增加,3种算法的相对定位误差趋于平稳,信标节点密度不再对定位误差产生较大影响。同时也可以看到,本文算法的相对定位误差比DV-Hop算法减小了很多;除了信标节点比例在5%到7.5%的小范围内,本文算法的相对定位误差比文献[15]算法略微大一点外,其他信标节点比例的相对定位误差均比文献[15]算法要小,说明本文算法的定位性能优于文献[15]算法;这是由于本文的跳数分类策略使得不同跳数的平均每跳距离更加精确,并且本文的权系数取值策略进一步减小了累积误差。

图7是通信半径R从15 m到45 m变化对定位误差影响的实验结果曲线,其中节点总数为300个,信标节点比例为10%。当网络节点密度一定时,较小的节点通信半径所对应的相对定位误差较大,因为节点通信半径较小时,容易导致网络的拓扑分布不均;但随着节点通信半径的增加,位于节点通信半径内的节点将增多,从而降低网络拓扑的分布不均,而拓扑更加规则必然会使得定位精度提高。从图7可以看出,当通信半径R=15 m时,DV-Hop算法的相对定位误差为41%,文献[15]算法的相对定位误差为26%,本文算法的相对定位误差为24%,说明本文算法的定位性能优于DV-Hop算法和文献[15]算法。从图7曲线可以看出,DV-Hop算法、文献[15]算法和本文算法的相对定位误差随着节点通信半径增加而逐渐下降;但是当节点通信半径增加到30 m左右时,随着通信半径的增加,3种定位算法的相对定位误差都趋于平稳,即当节点的通信半径增加到一定值时,节点定位误差受节点通信半径的影响逐渐减低。这是因为当节点的通信半径增大时,位于节点通信范围内的节点会增多,进而使得网络拓扑更加规则;但节点的通信半径增加到一定的值后,对节点的路径选择已经没有多大的影响,所以定位误差曲线趋于平稳。

图7 节点通信半径对定位误差影响

5 结论

①针对传统DV-Hop节点定位算法中平均每跳距离差异对节点定位精度影响的问题,提出一种跳数分类的策略,该策略将WSN中不同的跳数进行分类,并基于跳数分类来计算不同跳数之间的平均每跳距离,有效地提升了节点定位算法对不同网络节点密度的适应性以及节点定位的精度。

②为了减小随跳数增加而非线性增加的累积误差,提出一种改进的加权最小二乘估计权系数取值策略,该策略可以更好的适应累积误差的非线性变化,从而根据WSN中的跳数来自适应地调整不同跳数在最小二乘估计中的权重,有效地减小了因跳数增加而产生的累积误差,进一步提高了节点的定位精度。

③在不同节点总数、不同信标节点密度以及不同通信半径的算法仿真对比实验中,本文改进算法均表现出比传统DV-Hop节点定位算法更优异的性能,比相关对比文献中定位算法的性能也有一定的提升,从而表明本文的改进策略可以有效提升DV-Hop节点定位算法的性能。如何进一步地降低不同跳数的平均每跳距离差异和累积误差对节点定位精度的影响是后续要重点研究的工作。

[1] 洪锋,褚红伟,金宗科,等. 无线传感器网络应用系统最新进展综述[J]. 计算机研究与发展,2010,47(s2):81-87.

[2] 黄亮,王福豹,段渭军,等. 基于距离重构的无线传感器网络多维定标定位算法[J]. 传感技术学报,2013,26(9):1284-1287.

[3] Halder S,Ghosal A. A Survey on Mobile Anchor Assisted Localization Techniques in Wireless Sensor Networks[J]. Wireless Networks,2016,22(7):2317-2336.

[4] 雷高祥,黄辉,方旺盛. 基于RSSI值跳数修正和跳距加权处理的DV-HOP算法[J]. 江西理工大学学报,2015,36(5):80-84.

[5] 钱志鸿,王义君. 面向物联网的无线传感器网络综述[J]. 电子与信息学报,2013,35(1):215-227.

[6] Mao G,Fidan B,Anderson B D O. Wireless Sensor Network Localization Techniques[J]. Computer Networks,2007,51(10):2529-2553.

[7] 杨友华,孙丽华,向满天. 基于质点弹簧模型的无线传感器网络非测距定位算法[J]. 传感技术学报,2015,28(6):914-919.

[8] Niculescu D,Nath B. DV Based Positioning in Ad Hoc Networks[J]. Telecommunication Systems,2003,22(1-4):267-280.

[9] Zhao L Z,Wen X B,Li D. Amorphous Localization Algorithm Based on BP Artificial Neural Network[M]. Taylor and Francis,Inc,2015.

[10] 汤文亮,周琳颖. 基于三角形外接圆覆盖的改进APIT定位算法[J]. 传感技术学报,2015,28(1):121-125.

[11] Song G,Tam D. Two Novel DV-Hop Localization Algorithms for Randomly Deployed Wireless Sensor Networks[M]. Taylor and Francis,Inc.,2015.

[12] 程超,钱志鸿,付彩欣,等. 一种基于误差距离加权与跳段算法选择的遗传优化DV-Hop定位算法[J]. 电子与信息学报,2015,37(10):2418-2423.

[13] 黄以华,赵汝威,陈小若. 一种具有阶段优势的无锚点定位算法[J]. 电子学报,2015,43(12):2536-2541.

[14] S Ren W,Zhao C. A Localization Algorithm Based on SFLA and PSO for Wireless Sensor Network[J]. Information Technology Journal,2013,12(3):502-505.

[15] Kumar S,Lobiyal D K. An Advanced DV-Hop Localization Algorithm for Wireless Sensor Networks[J]. Wireless Personal Communications,2013,71(2):1365-1385.

[16] Gui L,Val T,Wei A,et al. Improvement of Range-Free Localization Technology by a Novel DV-Hop Protocol in Wireless Sensor Networks[J]. Ad Hoc Networks,2015,24:55-73.

ImprovedDV-HopNodeLocalizationAlgorithmBasedonHopCountClassification

RENKeqiang*,LIAOMeiyan

(School of Information Engineering,Jiangxi University of Science and Technology,Ganzhou Jiangxi 341000,China)

The different network node densities made larger difference among average single-hop distance of different hop count values in traditional DV-Hop node localization algorithm,and the error increased with the increase of the hop count value. An improved DV-Hop algorithm was proposed to reduce the influence of the average single-hop distance difference on the node localization accuracy. Firstly,the strategy of hop count classification was proposed to classify the different hop counts in the network,so as to reduce the difference of average single-hop distance between different hop counts,and to enhance the accuracy of node localization. Then,by using the strategy of the improved weight coefficient,the weighted least squares estimation was improved to adapt to the nonlinear variation of the cumulative error,which could better control the weight of the different hop counts in the least squares estimation,and further enhance the accuracy of node localization. The experimental results show that the improved algorithm can effectively reduce the influence of the average single-hop distance difference and the large hop count value on the node localization,its node localization performance is obviously superior to traditional DV-Hop node localization algorithm,compared with comparative literature also has a certain improvement,and it has better adaptability to different network node densities.

wireless sensor network;node localization;DV-Hop algorithm;hop count classification;weighted least squares estimation

TP393

1004-1699(2017)10-1565-07

10.3969/j.issn.1004-1699.2017.10.019