深水悬链线式柔性立管参数敏感性分析

揭晓侠, 李家旺, 朱克强, 刘 建

(宁波大学 海运学院, 浙江 宁波 315211)

2017-04-25

国家自然科学基金(11272160)；国家自然科学基金青年项目(51309133)

揭晓侠(1990—)，男，江西玉山人，硕士生，主要从事海洋工程挠性管线结构动态响应研究。E-mail:jie123xiao456@126.com

李家旺(1981—),男,安徽望江人,副教授,研究方向为船舶与海洋结构物流体与结构物动力学性能、运动控制。

E-mail:lijiawang@nbu.edu.cn

1000-4653(2017)03-0039-05

深水悬链线式柔性立管参数敏感性分析

揭晓侠, 李家旺, 朱克强, 刘 建

(宁波大学 海运学院, 浙江 宁波 315211)

针对柔性立管所处的深水环境，选取应用较为广泛的悬链线式布置方法，在特定的海洋环境中，在大型有限元软件OrcaFlex上建立悬链线立管模型进行动力分析。选取悬挂角、立管末端锚固点位置和管内流体等关键参数进行参数敏感性分析。结果表明：悬挂角的变化对立管顶部曲率有作用，但立管底部曲率和最大张力对悬挂角的变化不敏感；立管末端锚固点位置变化对立管动力响应有明显影响，布置立管时需重点考虑；立管曲率和弯矩对管内流体密度及流速的变化不敏感，但立管最大张力随管内流体密度的增大而减小，随管内流速的增大而增大。

悬链线； 柔性立管； 敏感性分析； OrcaFlex

海洋浮式生产系统由浮式生产平台、立管和系泊系统组成。柔性立管是一种由金属铠装螺旋缠绕聚合物圆柱组成的多层复合结构，各层间非黏结、可滑动，具有优良的弯曲性能。[1]柔性立管的上端与浮式平台铰接，下端与水下井口铰接，实现两者间的油气传输；其适用水深可达3 000 m，可承受70 ℃的高温和70 MPa的高压。[2]柔性立管能代替刚性立管应用于深海石油开采中的原因在于其能大曲率弯曲，因而对浮式生产平台的运动具有良好的顺应性。

对柔性立管进行动态分析采用的方法有别于刚性立管，原因在于柔性立管的轴向刚度可比弯曲刚度大5个数量级，致使一般的有限元刚度法易产生数值病态系数矩阵，导致不良或不稳定的计算产生，且在时域中应用有限元法一般会产生复杂的程序。[3]凝集质量法可避免出现大系统耦合方程，展现出一定的优越性。柔性立管结构见图1。

王安娇等[3]利用集中质量法建立一种能考虑管内流体流动情况的非线性动力分析方法。孙丽萍等[4]基于集中质量法建立深水S型铺管的三维数值模型，对其进行求解，并将其与利用商业软件OrcaFlex得到的结果相对比，验证程序的正确性。IWONA等[5]利用改进型刚性有限元方法离散细长构件预测立管运动，考虑水动力和附加质量的影响，与解析解和商业软件结果相对比，证明方法的正确性。KORDKHEILI等[6]利用三维环形梁的拉格朗日有限元公式进行立管大位移和大扭转动力分析，考虑浮力和稳态流的影响，将结果与其他文献结果相比对。CHAI等[7]得到考虑弯曲和扭转刚度的立管三维集中质量公式，可广泛应用在系泊缆和立管上，并可解决与海床接触的问题。

研究结果表明，在一般水深的作业环境中，由于悬链线布置具有结构简单、施工方便、成本较低及对浮体运动的适应能力强等特点，故其是海洋管线布置的首选。[8]文献[9]针对管道弯矩与曲率的非线性关系研究悬链线柔性立管的动力时域分析问题，但没有考虑管内流体的影响。因此，这里在大型水动力学软件OrcaFlex上建立悬链线柔性立管模型，重点考虑管内液体对立管的影响，同时分析悬挂角和锚固点位置等参数对立管动态响应的影响。

1 理论基础

图2为凝集质量法示意。[9]管道被分成若干个无质量段，每段的两端都有1个节点。无质量段只模拟管道轴向特性，其他(诸如质量、质量和浮力)全部集中到节点上。一般的凝集质量模型仅考虑弹簧刚度，没有计入阻尼特性，与实际立管差异较大。OrcaFlex上管道模型见图2。在无质量段中间由轴向弹簧和阻尼来模拟管道的轴向刚度及阻尼。弯曲特性则由节点两边旋转的弹簧和阻尼来模拟。

1.1有效张力的计算

有效张力的计算式为

Te=EA·ε+(1-2ν)(P0A0-PiAi)+

EA·C(dL/dt)/L0

(1)

式(1)中：EA为管道轴向刚度，等于杨氏模量与截面积的乘积；ε为总平均轴向应变，ε=(L-λL0)/(λL0)；L为管段瞬时长度；λ为管段的膨胀系数；L0为管段初始长度；ν为泊松比；Pi,P0分别为内压力和外压力；Ai,A0分别为内截面积和外截面积；C为阻尼系数；dL/dt为长度变化率。

阻尼系数C表示管道的数值阻尼，其计算式为

C=(λa/100)Ccrit

(2)

式(2)中：λa为目标轴向阻尼；Ccrit为管段临界阻尼值，Ccrit=(2ML0/EA)1/2。

a) 缆索模型简单示意

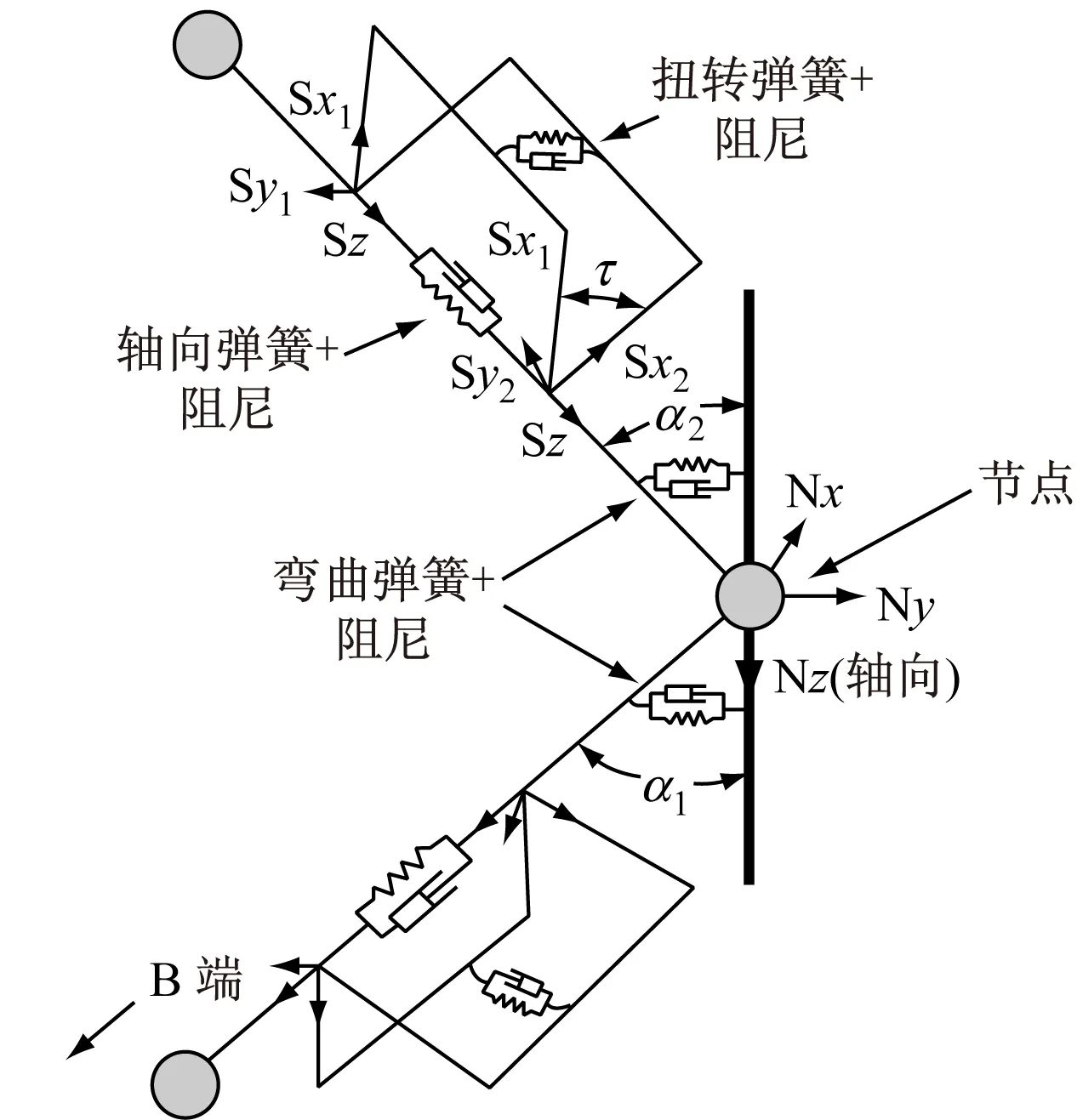
b) 缆索模型详细示意

1.2弯矩的计算

弯矩的计算式为

|M2|=EI·|C|+D·d|C|/dt

(3)

式(3)中：EI为弯曲刚度；D=(λb/100)Dcrit；λb为目标弯曲阻尼；Ccrit为管段弯曲临界阻尼值，Ccrit=L0(M·EI·L0)1/2；M为管段质量，含管内流体。

1.3动力计算方法

运动方程为

M(p,a)+C(p,v)+K(p)=F(p,v,t)

(4)

式(4)中：M(p,a)为系统惯性载荷；C(p,v)为阻尼载荷；K(p)为刚度载荷；F(p,v,t)为外部载荷。

在隐式解法中，力、力矩、阻尼和质量等参数的计算方法与显式解法相同，系统运动方程在时间步结束时被求解出。由于在时间步长结束时节点的位移、速度和加速度都未知，因此需用到迭代法。相应地，每一隐式时间步长相对于显式需更长的计算时间，但隐式解法对于时间步较长的情况更加稳定和快速。因此，采用隐式解法对立管进行动力计算。

2 数值模型

在OrcaFlex上建立柔性立管悬链线式模型。立管顶端距离水面166 m，与SPAR平台底端固接，通过设置立管的连接刚度为无穷大完成。立管末端锚定在不远处海底，与海底的轴向摩擦系数设置为0.25。立管总长1 850 m,设置不同的立管分段，以便对敏感受力区进行分析。因此，顶端100 m和触底段100 m划分为1 m长的小段单元，而悬垂段和海床静态立管划分为5 m长的小段单元。

1 500 m柔性立管系统布置简图见图3，相关参数见表1～表3。坐标系统见图4，分为全局坐标系和局部坐标系。立管底部末端X的位置是相对于全局坐标系而言的。波浪方向的定义见图5。

图3 1 500 m水深柔性立管系统布置简图

参数数值立管长度/m1850顶端脱离角度/(°)8硬舱直径/m30．50硬舱高度/m74．60参数数值软舱尺寸/m30．48×30．48软舱高度/m12主桁架/m93．20重心深度/m68

表2 柔性立管参数

表3 环境参数

图4 坐标系统

图5 波浪方向的定义

3 敏感性分析

设定悬挂角为10°，立管末端锚固点X坐标为653 m,管内流体密度为1 t/m3,流速为0.1 t/s，在5个波浪周期内进行时域仿真，得到立管动力响应见图6。

由图6可知，立管有效张力沿弧长方向不断减小。立管有效张力主要来自于其自身悬挂质量，因此立管顶部张力值最大。沿着弧长方向，悬挂长度减小，立管张力随之减小，在触底点以后保持不变。立管曲率在顶点处和触底点处有极大值，弯矩变化规律正比于曲率变化规律，也在顶点处和触底点有极大值。顶点处的最大曲率值(0.25)比触底点处的最大曲率值(0.003 8)大100倍，而两者的弯矩仅相差12.3倍，原因在于模型中立管采用非线性弯曲刚度。弯曲刚度见图7。

a) 有效张力

b) 曲率

c) 弯矩

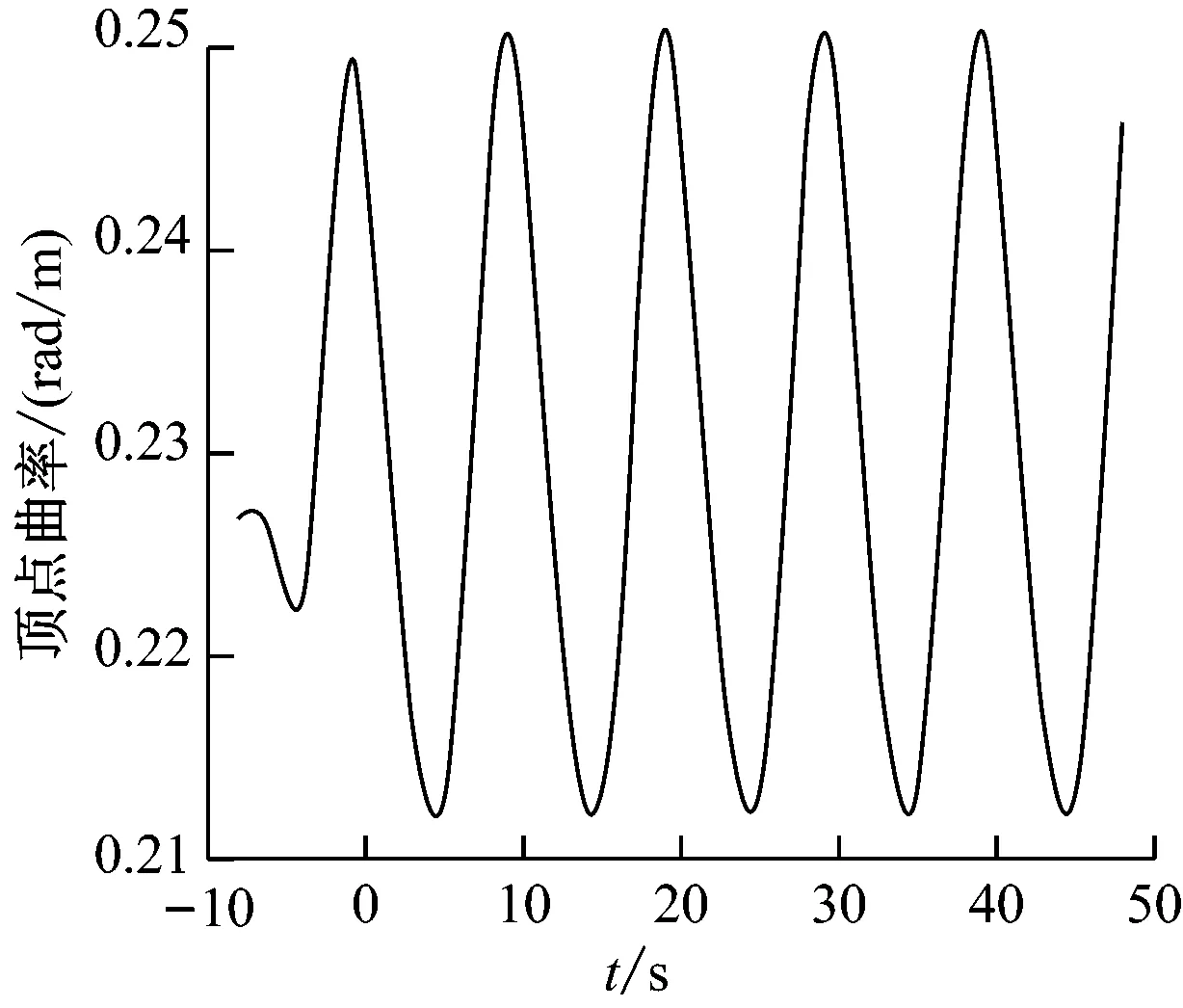
d) 顶点曲率

图6 立管动力响应

3.1改变悬挂角

为分析立管系统对悬挂角的敏感性[10]，悬挂角分别取6°,8°,10°,12°,14°和16°。在5个波浪周期内进行仿真，得到不同悬挂角下立管的曲率、弯矩和最大张力见图8。

由图8可知：随着悬挂角的增大，立管顶点曲率先减小后增大，触底点曲率保持不变；弯矩的变化规律与曲率的变化规律一致；立管最大张力始终保持在恒定值。由此可知，悬挂角只对立管顶部有明显的作用，立管触地部分和立管最大张力对悬挂角的变化不敏感。

图7 立管弯矩随曲率变化

3.2锚固点变化

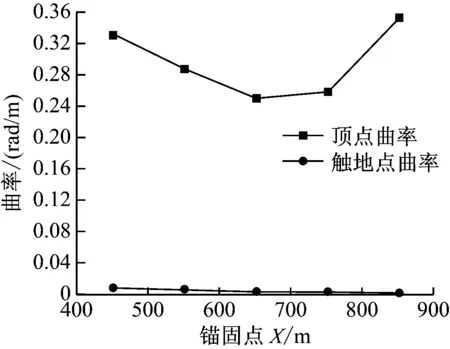
为分析立管系统对立管末端锚固点的敏感性，分别设定锚固点X坐标为453 m,553 m,653 m,753 m和853 m。不同锚固点下立管的曲率、弯矩和最大张力见图9。

a) 曲率

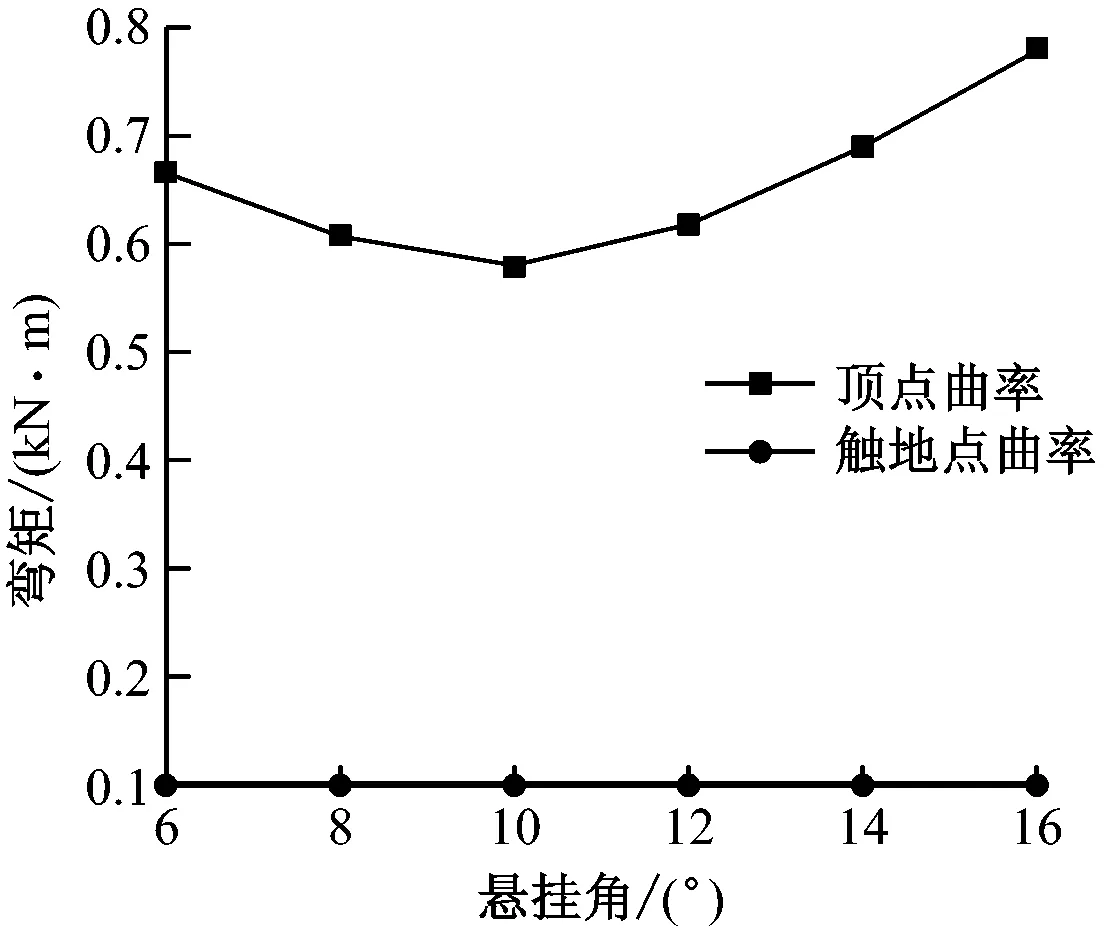
b) 弯矩

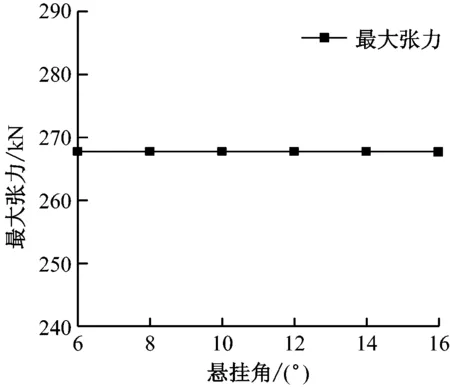
c) 最大张力

a) 曲率

b) 弯矩

c) 有效张力

由图9可知，随着立管末端锚固点X坐标的增大，立管顶点的曲率先减小后增大，立管触地点曲率持续减小，弯矩变化规律与曲率变化规律一致。最大张力随着锚固点的远离而线性增大。因为随着锚固点的远离，立管的悬挂长度变长，所以最大张力会增大，而立管触地点会更加平缓，立管触地点的曲率会减小。

3.3管内流体密度和流速变化

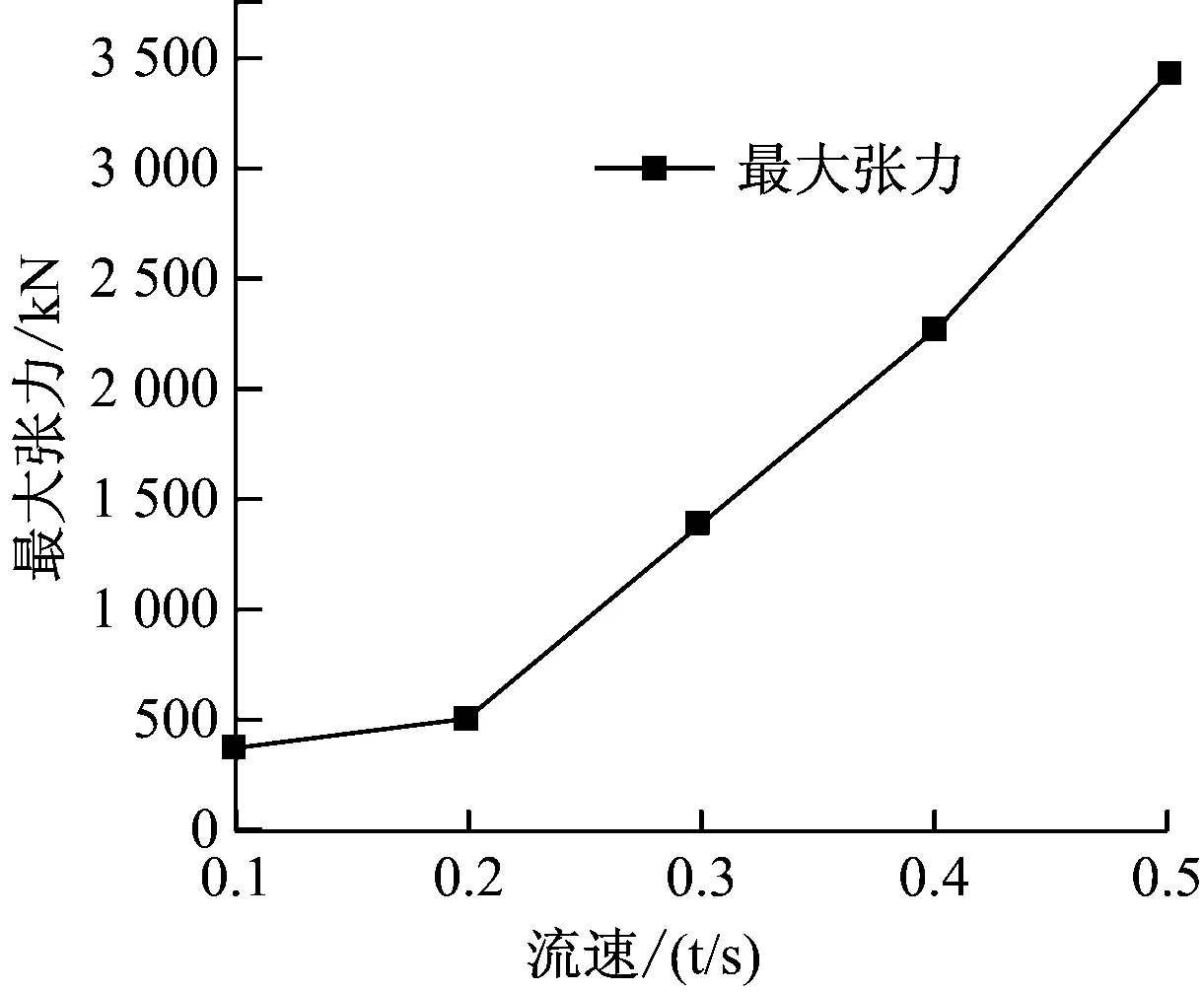
表6为不同管内流体密度下立管的曲率、弯矩和最大张力，表7为不同管内流速下立管的曲率、弯矩和最大张力，图10为最大张力随管内流体密度和流速的变化。

表6 不同管内流体密度下立管曲率、弯矩和最大张力

表7 不同管内流速下立管曲率、弯矩和最大张力

a) 最大张力随流体密度的变化

b) 最大张力随流速的变化

由表6、表7和图10可知:立管的曲率和弯矩对管内流体的密度及其流速的变化不敏感;但是,立管的最大张力随着管内流体密度的增大而减小，随着管内流体的流速增大而增大;当立管内流体的密度增加时，相当于立管变重，立管悬挂长度变小，因此立管最大张力减小。

4 结束语

在深水石油工程实践中,柔性立管正日益取代刚性立管；而悬链线布置法安装简单、成本较低，成为海洋工程立管敷设的首选。在大型水动力学软件OrcaFlex上建立深水柔性立管悬链线模型，通过对悬挂角、立管末端锚固点位置和管内流体等关键参数进行参数敏感性分析，得到以下结论：

1) 悬挂角只对立管顶部曲率有明显作用，立管触地部分曲率和立管最大张力对悬挂角的变化不敏感。

2) 随着立管末端锚固点的远离，立管悬挂长度增加，立管顶点曲率先减小后增大，立管触地点曲率持续减小，弯矩变化规律与曲率变化规律一致，最大张力线性增大。

3) 立管的曲率和弯矩对管内流体的密度及其流速的变化不敏感。但是，立管的最大张力随着管内流体密度的增大而减小，随着管内流体流速的增大而增大。

[1] 卢青针,冯俐,阎军. 考虑非线性弯曲刚度的柔性立管时域分析[J]. 哈尔滨工程大学学报, 2013,34(11):1352-1356.

[2] 丁鹏龙,李英,刘志龙. 陡波型柔性立管浮力块参数优化及应用[J]. 海洋工程, 2014,32(4):18-23.

[3] 王安姣,陈加菁. 柔性立管的非线性动力分析[J]. 海洋工程, 1991,9(3):12-22.

[4] 孙丽萍,宋环峰,艾尚茂. 基于集中质量法的深水S型铺管动力响应研究[J]. 中国海洋平台, 2015,30(2):70-76.

[5] IWONA A W, LUCYNA B, LUKASZ D. An Analysis of Dynamics of Risers During Vessel Motion by Means of the Rigid Finite Element Method[J]. Ocean Engineering,2015,106:102-114.

[6] KORDKHEILI H S A， BAHAI H， MIRTAHERI M. An Updated Lagrangian Finite Element Formulation for Large Displacement Dynamic Analysis of Three-Dimensional Flexible Riser Structures[J]. Ocean Engineering,2011,38(5-6):793-803.

[7] CHAI Y T, VARYANI K S, BARLTROP N D P. Three-Dimensional Lump-Mass Formulation of a Cate-nary Riser with Bending, Torsion and Irregular Seabed Interaction Effect[J]. Ocean Engineering,2002,29(12):1503-1525.

[8] 陈希恰,宋磊建,杜夏英,等. 深海脐带缆总体响应特性研究[J]. 海洋工程装备与技术,2015,2(2):111-117.

[9] Orcina. OrcaFlex Manual: Version 9.7a[M]. Cumbria: Orcina, 2012.

[10] 孙丽萍，周佳，王佳琦. 深水柔性立管的缓坡型布置及参数敏感性分析[J]. 中国海洋平台, 2011,26(3):37-42.

ParameterSensitivityAnalysisofCatenaryFlexibleRiserinDeepWater

JIEXiaoxia,LIJiawang,ZHUKeqiang,LIUJian

(Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211, China)

For deep-water environment of flexible riser, the commonly used catenary configuration is selected. In the specific ocean surroundings, the model of catenary riser is built with finite element software OrcaFlex. Parameter sensitivity analysis is made with the variation of top angle, mooring point and flow inside riser. Results show: the variation of top angle can affect the curvature of a top riser, while curvature of touch down point and max tension are not sensitive to it; Riser mooring point has clear influence on dynamic response of riser, which needs additional considerations; the curvature and bend moment of the riser are not sensitive to the variation of density and velocity of flow inside riser, but maximum tension decreases with the increasing density and increases with increasing velocity.

catenary; flexible riser; sensitive analysis; OrcaFlex

P756.2

A