An ISPH model for flow-like landslides and interaction with structures *
2017-11-02DongfangLiang梁东方XuzhenHeJingxinZhang张景新
Dongfang Liang (梁东方), Xuzhen He, Jing-xin Zhang (张景新)
1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China,E-mail: d.liang@sjtu.edu.cn
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
3. Institut für Geotechnik, Universität für Bodenkultur Wien, Feistmantelstrasse 4, 1180 Wien, Austria
An ISPH model for flow-like landslides and interaction with structures*
Dongfang Liang (梁东方)1,2, Xuzhen He3, Jing-xin Zhang (张景新)1,2
1. State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China,E-mail: d.liang@sjtu.edu.cn
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
3. Institut für Geotechnik, Universität für Bodenkultur Wien, Feistmantelstrasse 4, 1180 Wien, Austria
An incompressible smoothed particle hydrodynamics (ISPH) model has been developed to investigate the flow-like landslide phenomena The landslide mass is idealized as rigid and perfectly-plastic material with a constant density. Unlike the widely-used explicit smoothed particle hydrodynamics (SPH) models for landslides, the Chorin's projection method is used herein to implicitly solve the normal stress via a pressure Poisson equation, leading to a realistic distribution of instantaneous stress fields free of spurious fluctuations. The capability of the model is demonstrated through three case studies, including the idealized granular flow,landslide interaction with a rigid barrier, and a historical cut-slope landslide in Hong Kong.
Landslides, smoothed particle hydrodynamics, granular flows, meshfree methods
Landslides involve the rapid downslope movement of soil mass under gravity. The widely-used mesh-based methods suffer from grid distortion,which leads to computational inaccuracy and numerical instability. As an alternative, the meshfree methods can easily cope with the large soil deformation. The smoothed particle hydrodynamics (SPH)method is probably the oldest meshfree method,which represents the continuum with a number of discrete particles[1-3]. Apart from avoiding the mesh tangling problem, the SPH method also has other attractive characteristics. It can significantly reduce computational costs, as discretization is only needed where the landslide mass is present rather than over the entire run-out space. The SPH method can easily track the history-dependent variables, as unknowns are defined on the moving particles.
Almost all the previous SPH models in soil mechanics employ explicit SPH schemes in a similar way to the weakly-compressible SPH models in computational fluid dynamics (CFD). Without complicated numerical treatments, such as pressure filter, viscous damping and stress regularization, they generate spurious stress oscillations, despite the accurately-predicted velocity field and thus continuum deformation.These nonphysical oscillations pose difficulties to the deployment of sophisticated constitutive models. The present study adopts an implicit SPH method, which has been proved to produce smooth stress field in CFD.
The motion of an incompressible continuum can be modelled by the governing equations below:
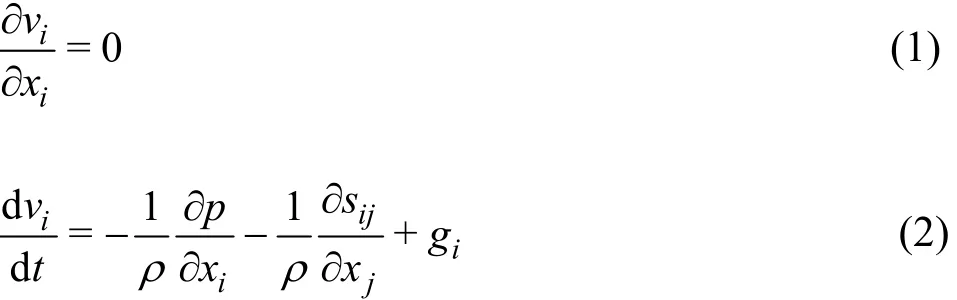
where t andix are time and spatial coordinate respectively, is density,iv is velocity, p is normal stress,ijs is deviatoric stress tensor,ig is gravitational acceleration.Here,weadopt the convention that compression is positive. Because soil in flow-like landslides should have undergone large deformations, it is expected to stay in the critical state.Hence, we ignore the stress ratio variation and dilatancy. Therefore, soil is modelled as an incompressible and rigid-perfectly plastic material with a Coulomb yield surface. With the coaxial assumption,the following relationship holds

wherecritφ is the internal friction angle,ij∈˙is the deviatoric strain rate tensor. This relationship is often referred to as the Drucker-Prager yield criterion. The strain rate tensor and itsdeviatoric counterpart are:

whereijδ is Kronecker delta. The projection method is used to solve the above equations by decoupling the velocity and normal stress calculations. This projection method was first implemented in CFD. It first considers only the gravity and deviatoric stress terms in the momentum equation to obtain an intermediate velocity field, which is subsequently modified to satisfy the incompressible condition. The intermediate and final velocities are:

where tΔ is the time step, the subscripts n, n*and +1n denote time levels. To guarantee incompressibility, the following Poisson equation is solved to updatethe normal stress,+1np

Finally, the particle's new position is updated according to the flow velocity.
Using the SPH approximation, each term in the partial differential Eqs.(6)-(8) can be expressed with the kernel functionWand its spatial derivatives∂W/∂ xi. In summary, the SPH discretization of the above equations gives:

where the superscript a represents the particle in consideration, b is the index of a neighbouring particle of a,eiN is the total number of neighbours in the support domain of particle a, m is the mass of a particle,abr is the distance between particles a and b,abW is the value of the kernel function between a and b, is a small value to prevent numerical instability when particles get very close.
In the landslide analysis, there are generally two types of boundaries: the free surface and the solid surface. The free surface boundary condition is implemented by first finding the free surface particles and then equating all stresses to zero. Wall particles and dummy particles are used to facilitate prescribing the solid boundary condition. The non-penetration condition is enforced at solid surfaces and the tangential drag force is equated to the normal reaction multiplied by the wall frictional coefficient. Detailed numerical treatments include the renormalized kernel and its gradient in the case of particle deficiency.
The first case study simulates the granular flow along a slope. The corresponding experiment used 50 liters of quartz sand, with an angle of repose (AOR) of 33o[4]. The slope angle was 5 0oand the drop height was 1.414 m. The sand was initially piled behind a gate perpendicular to the slope, which was suddenly lifted with an opening of 60 mm. Corresponding to the small opening, a thin layer of sand is observed on the slope, as shown in Figs.1(a), 1(b). The initial particle spacing is 4 mm, resulting in a total of 9 736 particles.The final deposition profile observed in the experiment is indicated with a thin solid line, which shows a slope angle in the middle section to be equal to the AOR. Figure 1(a) shows the moment when some soil has been deposited at the toe. The present model can satisfactorily reproduce the flow onto the horizontal plane, with a correct shape of the final deposition.This example also highlights some discrepancies in the cross-sectional area, which reveal the limitations of the present model. The incompressible model cannot reproduce the volume change of the collapsed material. In reality, granular materials may contract or dilate, depending on its initial state, to a critical state void ratio during mobilization. The experimental result in Fig.1 shows around 10% increase in the final cross-sectional area of the deposition.

Fig.1 Releasing granular material on a slope, together with the measured deposition profile
For some hillside cities with a high population density, passivemitigation measures may prove to becost-effective. A series of dry granular were performed to study the landslide impact on rigid barriers (Fig. 2a). 50 kg of Toyourasand was used,with a bulk density of 1379 The sand was initi ally co nfinedin a rect angu lar box o f le ngth 0.5 m andheight0.3 m.Itwasthenreleasedtoflowalong the slope and eventually hit a rigid barrier normalto the slope. The distance between the gate and the barrier is 1.8 m, and the height of the barrier is 0.3 m.We considers the case with a slope angle ofo45.

Fig.2 (Color online) Interaction of landslide with a rigid barrier at the toe
The initial particle spacing is 3.6 mm, resulting in 10 164 particles.cirtφis set too44. Figures 2(b),2(c) show the predicted velocity fields at two typical instants. The sand is seen to stretch into a thin layer along the slope and then deposit progressively in front of the barrier. Later particles impact on the wedge-shaped static zone, which grows with time.Figure 2(d)shows good comparison between measured and predicted forces.
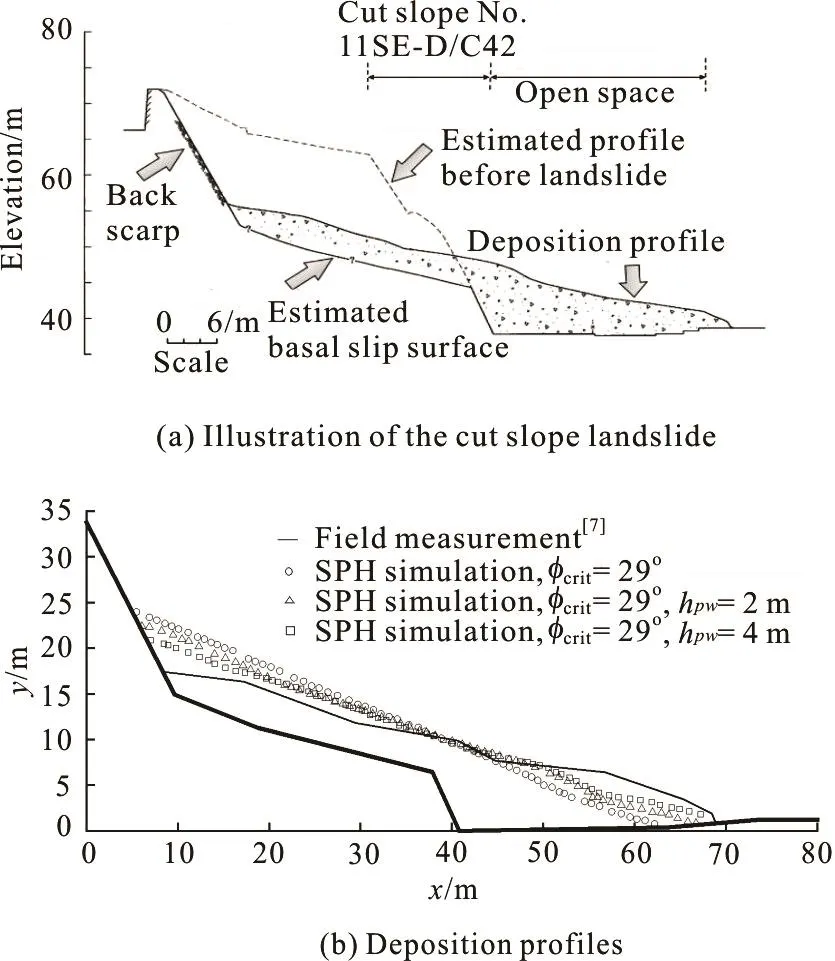
Fig.3 A cut slope landslide near FeiTsui Road, Hong Kong on 13 August, 1995
The final case study considers the FeiTsui cut-slope landslide in Hong Kong. The width of the landslide was 90 m, with a cross-section shown i3n Fig.3(a). The landslide volume was about 14 000 m,making it the largest fast-moving cut-slope failure in Hong Kong. The landslide was caused by heavy rain,and the increased groundwater pressure triggered the event. The slope was mainly composed of weathered rock, whose peak strength envelope in terms of effective stress implied an internal friction angle of 35o[6]. A weak layer was identified at the basal slip surface, consisting of 0.5 m thick kaolinite-rich tuff with low permeability. Laboratory tests showed that the average internal friction angle of this layer was 29oin terms of the effective stress[6].
In this case, the mobility enhanced by the pore water pressure cannot be ignored. An equivalent friction coefficient is implemented to account for this effect. The pore pressure is denoted by u and the stress tensor can be expressed asσij= u δij+ σi′j. Here,σi′jis the effective stress of the soil which is governed by Eq.(3). Consequently, the equivalent friction coefficient is calculated as

Assume an initial layer of water with heightpwh flowing uniformly above the basal kaolin layer. The values ofu andp′ are then estimated as in an infinite landslide model, allowingthe equivalent friction angle to be calculated. We further assume that these initial pore pressures remain unchanged as the slide progresses. Whenpwh is assumed to be 2 m,eφ at the basal slip surface is 2 3 .24o. When increasingh topw4 m, thisφ drops to 22.33o. Fig. 3(b) indicates aepositive correlation between the water table height and the run-out distance. With an initial water depth of 4 m, the predicted deposition profile agrees well with the field observation. This analysis largely agrees with the static slope stability analysis[6]. Considering the uncertainties regarding the soil's initial condition and the excess pore pressure variation, it is encouraging that this simple model is capable of giving reasonable predictions.
In summary, a projection method is used to solve the continuum mechanics equations for predicting rapid landslide phenomena in an SPH framework. The normal stress is calculated implicitly via a Poisson equation. It has the advantage over the explicit SPH models by obtaining a smooth stress field without any complicated treatments. Its drawback lies in its inability to consider the soil dilation and the void ratio variation with the normal stress.
[1] Liang D. Evaluating shallow water assumptions in dambreak flows [J]. Proceedings of the Institution of Civil Engineers-Water Management, 2010, 163(5): 227-237.
[2] Liu M. B., Li S. M. On the modeling of viscous incompressible flows with smoothed particle hydrodynamics [J].Journal of Hydrodynamics, 2016, 28(5):731-745.
[3] Zhang A. M., Sun P. N., Ming F. R. et al. Smoothed particle hydrodynamics and its applications in fluid-structure interactions [J]. Journal of Hydrodynamics, 2017,29(2): 187-216.
[4] Pudasaini S. P., Hutter K., Hsiau S. S. et al. Rapid flow of dry granular materials down inclined chutes impinging on rigid walls [J]. Physics of Fluids, 2007, 19(5): 053302.
[5] Moriguchi S., Borja R. I., Yashima A. et al. Estimating the impact force generated by granular flow on a rigid obstruction [J]. Acta Geotechnica, 2009, 4(1): 57-71.
[6] GEO. Report on the FeiTsui road landslide of 13 August 1995 [R]. Hong Kong, China: Geotechnical Engineering Office, 1996, 156.
April 16, 2017, Revised July 7, 2017)
* Project supported by the National Natural Science Foundation of China (Grant No. 51479111), the Ministry of Education and State Administration of Foreign Experts Affairs 111 Project (Grant No. B17015).
Biography: Dongfang Liang (1975-), Male, Professor
杂志排行
水动力学研究与进展 B辑的其它文章
- On the clean numerical simulation (CNS) of chaotic dynamic systems *
- BEM for wave interaction with structures and low storage accelerated methods for large scale computation *
- Flow-pipe-soil coupling mechanisms and predictions for submarine pipeline instability *
- Simulation of flows with moving contact lines on a dual-resolution Cartesian grid using a diffuse-interface immersed-boundary method *
- On the hydrodynamics of hydraulic machinery and flow control *
- A 3-D SPH model for simulating water flooding of a damaged floating structure *
