Effect of polymer and fiber additives on pressure drop in a rectangular channel *
2017-11-02AmirEshghinejadfardKashyapaSharmaDominiqueThvenin
Amir Eshghinejadfard, Kashyapa Sharma, Dominique Thévenin
Laboratory of Fluid Dynamics and Technical Flows, University of Magdeburg “Otto von Guericke”,Universitätsplatz 2, 39106 Magdeburg, Germany, E-mail: amir.eshghinejadfard@ovgu.de
Effect of polymer and fiber additives on pressure drop in a rectangular channel*
Amir Eshghinejadfard, Kashyapa Sharma, Dominique Thévenin
Laboratory of Fluid Dynamics and Technical Flows, University of Magdeburg “Otto von Guericke”,Universitätsplatz 2, 39106 Magdeburg, Germany, E-mail: amir.eshghinejadfard@ovgu.de
The influence of minute amounts of additives on pressure drop is an interesting fundamental phenomenon, potentially with important practical applications. Change of the pressure drop in a quasi-two-dimensional channel flow using various additives is experimentally investigated. Tests were conducted for a wide range of concentrations (100 ppm-500 ppm) and Reynolds numbers(16 000-36 000) with two polymers and four rigid fibers used as additive. Maximum drag reduction of 22% was observed for xanthan gum. However, xanthan gum loses its drag-reducing property rapidly. It was also seen that drag reduction percentage of xanthan gum remains almost constant for different Reynolds numbers. Guar flour demonstrated good drag reduction property at high Reynolds numbers. Drag reduction of 17.5% at R e = 33200 using 300 ppm solution was observed. However, at low Reynolds numbers guar flour will cause an increase in pressure drop. Fiber fillers (aspect ratio=21) have been tested as well. In contrast to polymers, they increased the drag for the range of examined concentrations and Reynolds numbers. Polyacrylonitrile fiber with three different aspect ratios (106, 200, 400) was also used, which showed an increase in pressure drop at low aspect ratios. Polyacrylonitrile fibers of larger lengths (6 mm) demonstrated minor drag-reducing effects (up to 3%).
Pressure drop, polymer, fiber, channel flow
Introduction
Effect of suspended particles and additives on flow properties is always an important topic for both experimental and numerical studies. In this regard,some types of additives lead to lower pressure drop in the flow[1-3]while some others increase it[4,5]. Particle and fluid type in addition to flow regime and geometry play the main roles in this regard. Therefore, recognizing the conditions that can result in reduction or enhancement of pressure drop is of great importance.
Reduction of pressure drop and consequently pumping cost is an interesting topic for many liquid transportation systems. This can be achieved by addition of small amounts of drag-reducing agents(DRA)[6]. The concept of drag reduction (DR) can be traced back to the work of Toms[7]. He discovered that introduction of a few parts per million (ppm) of longchain polymers can result in reduction of wall friction.DR leads to an increase of pipeline flow rate for the same pressure head. Most studies focus on polymers as drag reduction agent[8-11]. In this regard, long-chain and flexible polymers such as polyacrylamide and polyethylene oxide (PEO) are recognized as DRA.Onset of DR occurs when polymers are unraveled from the coiled to an extended conformation. Therefore, DR due to polymer solutions is expected to happen beyond a certain Reynolds number for a unique concentration. Below this Reynolds number usually no DR is observed.
Two types of explanation have been given for the onset of DR when polymers are utilized. Some researchers[12-14]attribute DR to viscous effects. They reason that stretching of polymers in the regions of strong deformations of flow field leads to a higher effective viscosity in this turbulent region and consequently the thickness of buffer region is increased and velocity gradient is reduced. On the other hand, the elastic theory of Tabor and De Gennes[15]postulates that DR occurs when the elastic energy of polymers is large enough to terminate the Kolmogorov-type energy cascade. A major practical problem associated with flexible polymers is their fast thermal, biological, chemical, or mechanical degradation. This would limit their application to one-passsystems. Nowadays, rigid polymers[16], surfactants[17],bubbles[18], nanoparticles[19]and fibers[20,21]have been proven as possible alternatives for flexible polymers.
In most cases from dilute to dense regimes,however, pressure drop increases after addition of rigid particles[22-27]. This effect is highly dependent on particle shape, Stokes number ()St and solid phase volume fraction ()φ. There are many practical cases,in which, fibers or polymers are transported by the piping system. It would be thus important to recognize the conditions that can lead to each of above mentioned pathways and to understand the effect of different additives on decrease or increase of pressure drop.
The current work aims at experimentally investigating the influence of different additives on pressure drop in a straight rectangular channel. The experimental set-up includes a long channel of rectangular cross section to mimic a quasi-two-dimensional flow.Pressure drop measurements are performed and results are compared with those of pure water to calculate the pressure drop change. The first part of the results deals with behavior of semi-rigid polymers (xanthan gum, guar flour) and investigates their effect for different flow rates. Since less attention has been paid to rigid particles so far, the second part considers the effect of rigid particle shape, concentration and size on pressure drop in semi-dilute regime. In the end, we aim to arrive at a final method on the selection of rigid fibers to lower the pressure drop in particle-laden systems.
1. Turbulent channel flow characteristics
For theoretical calculations, a fully developed turbulent flow through a channel is assumed in this study. Pressure drop and flow characteristics are thus related through
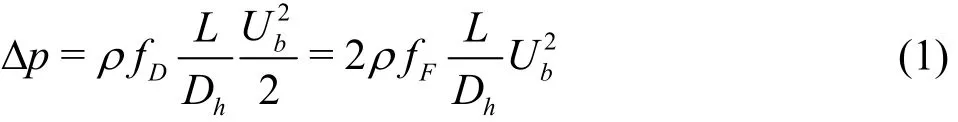
where is the fluid density,Df is Darcy friction factor,Ff is Fanning friction factor, L is distance,Dhis the hydraulic diameter and Ubis the mean(bulk) velocity. Due to large width to height ratio of the channel, Dhis considered to be equal to 4H with H being the half-channel height. Consequently,the friction velocity (uτ) is given by

withwτ being the mean shear stress at the wall and Δ p a constant pressure gradient. The Reynolds number based on the friction velocity reads

where is the fluid kinematic viscosity. The bulk Reynolds number is given based on the channel height by

The Fanning friction factor for turbulent fluid flow in smooth pipes is usually described by the Prandtl-von Karman (PK) expression[28]

In the case of water as carrier fluid, the Blasius approximation can be used as well

Based on the Virk's maximum drag reduction(MDR) asymptote[29], the lowest friction factor that can be attained in a turbulent flow is defined by
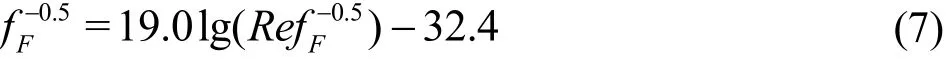
Therefore, the friction factor of a drag-reducing system must fall between the PK law and Virk's MDR asymptote for a given Reynolds number. In multiphase flows, DR percent is defined as the ratio of reduction in the pressure drop to the pressure drop without DRA

Here, subscripts 0 and DR denote the states in the absence and presence of DRA, respectively. Both pressure drops are measured at the same Reynolds number based on water properties.
Another important parameter in particle-laden turbulent flows (mainly for rigid particles) is the particle Stokes number. It is defined as the ratio of the particle response time (τp) to the characteristic time scale of the turbulent flow. A particle with low Stokes number responds quickly to the flow. Characteristic time scale of the fluid flow can be either theone is denoted by S tKand the latter one by S t+.Elghobashi[30,31]presented a classification map for particle-laden turbulent flows based on the volume fraction and Stokes number. This map shows whether the turbulent kinetic energy (TKE) in the presence of particles in dilute regime will increase or decrease.For dilutesuspension of rigid particleshe recognized two main zones based on the Kolmogorov Stokes number. Normally, for very low Stokes numbers(Microparticles) TKE increases.Forparticles do not respond immediately to velocity fluctuations of surrounding fluid. Thus,reduction of both TKE and dissipation relative to the single-phase flow is expected. For10≥ , due to vortex shedding behind the particle, TKE increases.However, in dense regimes with finite-size particles reduction of TKE and Reynolds shear stress was observed[4,32]. In contrast to TKE whose changes can be distinguished based on the solid phase volume fraction and Stokes number, changes in the pressure drop show strong dependency on particle shape and Reynolds number as well. It means that reduction of turbulence intensity does not necessarily lead to drag reduction and many other parameters must be considered. For example, in numerical studies of Zhao and van Wachem[25], the turbulence kinetic energy decreased by 6.0% for the flow with spherical particles and by 4.8% for the ellipsoidal particles, but the mean flow velocity is reduced as compared with single-phase flow. These effects will be discussed in the following sections.

Fig.1(a) Sketch of the experimental set-up

Fig.1(b) Channel cross section
2. Experimental set-up and procedure
Figure 1(a) depicts a sketch of the experimental set-up. A rectangular channel is used as the main test section. Channel length is 6 m and its cross section is rectangular with aspect ratio of 200 mm to 10 mm(Fig.1(b)). A stainless steel tank, pressure transmitter,temperature sensor (thermometer), flow meter and flow regulating pump were used in the set-up as well.The set-up works as a closed loop where the fluid runs from an open stainless steel tank through aΦ50mm diameter pipe section followed by the channel, and finally returns to the tank. Transition from the circular cross section of the pipe to the rectangular section of the channel has very gentle slope to prevent any sudden change in the flow. The screw pump regulates the fluid flow rate.
The pressure drop measurements were performed between two pressure taps that are placed 1 m apart using a Hottinger-Baldwin differential pressure transmitter. To obtain a hydrodynamically fully developed flow region, the pressure sensors were located far (2.8 m) from the transition zone between circular and rectangular cross-section. The zero error of the sensors was noted before each measurement and subsequently used in the final results calculation. The thermometer installed on the discharge line of the tank records the temperature; the flow rate of the fluid is measured using a magnetic flow meter (Endress and Hauser). Tap water was used as working fluid and the influence of the following additives on the pressure drop was investigated:
(1) Xanthan gum, which is a high molecular weight polysaccharide with a semi-rigid structure.Its primary structure consists of repeated pentasaccharide units formed by two glucose units, two mannose units, and one glucuronic[33]. Xanthan gum increases the viscosity of the liquid when it is added in very low concentrations at moderate temperatures.Owing to its distinct rheological properties, it is known as an important industrial biopolymer and has broad applications in food and cosmetic products.The xanthan gum E-415 from Carl Roth Co. (size 80 mesh) was used in the experiments.
(2) Guar flour, from Carl Roth Co. (CAS 9000-30-0) was used. Guar flour mainly consists of high molecular weight polysaccharides with an average size of up to some hundred microns obtained from the guar plant seed and composed of watersoluble galactomannans which are formed from a linear chain of (14→)-linked β-D-mannopyranosyl units with (16→)-linked α-D-galactopyranosyl residues as side chains. Its main applications are in the food industry.
(3) Carbon filler, SFC-B10 (from Schwarzwälder Textil-Werke group) which is a short length carbon fiber consisting of very thin strands of the element carbon with density of 1 780 kg/m3was also tested. Its average diameter and length are 7 μm and 150 μm,respectively, which results in aspect ratio equal to 21.The elastic modulus of this fiber is 190 GPa.
(4) Polyacrylonitrile fiber, which is a high strength and high modulus of elasticity white-yellowish fiber from Schwarzwälder Textil-Werke group known as PAC251 with a specific gravity of 1.18 was used. It has various applications in textile, composite materials and aircraft industry. The fiber diameter is approximately 15 μm and available in various lengths.For the experiment, 1.6, 3 and 6 mm fibers at different concentrations were used. The elastic modulus of this type of additive is 10 GPa-12 GPa.
Different preparation procedures were used for individual additives. For xanthan gum, the required quantity of the gum was added directly into the tank and mixed for 30 min using a hydrofoil blade mixer(tank stirrer). The system was left alone for at least 24 h to let the gum dissolve gradually in the water.The drag-reducing capacity of the xanthan gum was not instantly retrieved. Therefore, the experiments were carried out with batches of 8 h continuous operation each. Above this duration, the DR effect of the xanthan solution decreased noticeably. For each concentration, the entire set-up was cleaned and a fresh batch of sample and water was used.
To obtain a homogeneous mixture for the fibers the samples were prepared outside the system. Small quantities of the sample (50 g-70 g) were dispersed in 3 to 5 liters of water and stirred using a small stirrer in a separate set-up. Small quantity of soap solution was used in order to obtain good dispersion of the sample.Batches of prepared sample solutions were later transferred into the main tank. Along with the above mentioned procedure, the tank stirrer was finally used for at least 2 h to obtain a homogeneous dispersed phase. For higher concentration, new batches of fiber solutions were added to the existing mixture. Each experiment took at least 3 h of continuous run.

Fig.2 Friction factor vs. Re for water and xanthan gum

Fig.3 DR percentage vs. Re for xanthan gum and carbon fillers
3. Experimental results
3.1Part I: Polymers
3.1.1 Xanthan gum
In this section the measurement results for water and 100 ppm and 200 ppm solutions of xanthan gum are presented. Friction factor versus Reynolds number is plotted in Fig.2. It is observed that, for the examined range of Reynolds number (Re=18000-36000), the pressure drop measured from water circulation is in close consistency with the Prandtl-von Karman (PK) correlation (Eq.(5)). Brown squares represent Virk's MDR theory (Eq.(7)). DR capability of xanthan gum can be clearly observed for both 100 and 200 ppm solutions. As expected, a higher DR percentage is achievable at higher concentrations of polymer.However,for current concentrations(100 ppm and 200 ppm) DR is lower than maximum DR asymptote.
On the other hand, it is seen that xanthan gum loses its effectiveness rapidly. In this regard, degraded solution of 200 ppm has a lower efficiency than 100 ppm fresh solution. This occurs after only 15 h of running the apparatus. DR percentage for various Reynolds numbers is reported in Fig.3. DR percentage is computed from Eq.(8) at the same temperature of water and xanthan solution to exclude the effect of temperature on water density and viscosity. It is seen that DR initially shows some dependency on Reynolds number but tends to reach a constant value. This transition to constant DR percentage occurs at higher Reynolds number when the polymer concentration is higher. Maximum DR percentage in the range of examined flow rates was observed atRe=33890 standing at 22% for a solution containing 200 ppm xanthan gum.
It must be noted that the current channel is rather narrow. In larger systems, use of higher concentrations of polymers is easier without formation of clumps. The reduced efficiency of polymers can be obviously observed from Fig.3. This reduction of efficiency is mainly attributed to de-aggregation of rigid polymers[34].
3.1.2 Guar flour
The next polymer that is studied in this part is guar flour. Two concentrations of 100 ppm and 300 ppm are considered. The results of changes in pressure drop are shown in Fig.4. This figure illustrates that guar flour does not demonstrate any drag reduction at Reynolds numbers less than 21 000.In the range of low Reynolds numbers, both concentrations led to pressure drop increase. A maximum increase of 9.4% was observed for 100 ppm guar gum solution. Furthermore, the amount of this increase is almost similar for both 100 ppm and 300 ppm solutions. AtRe≃ 2 2000 guar flour neither increases, nor decreases the pressure drop. At higher Reynolds numbers (Re>2 2000),a noticeable drag reduction is seen from the graph. Higher concentration (300 ppm) yields higher DR percentage.Its corresponding graph has a higher slope as well.This trend is approximated by a third order polynomial fit for both concentrations. One can get 17.5% drag reduction atRe= 33200 when 300 ppm guar flour is used. This percentage remained constant after 3 h of running the system. Maximum DR percentage attained by using 100 ppm solution was 10.8% atRe= 31300.
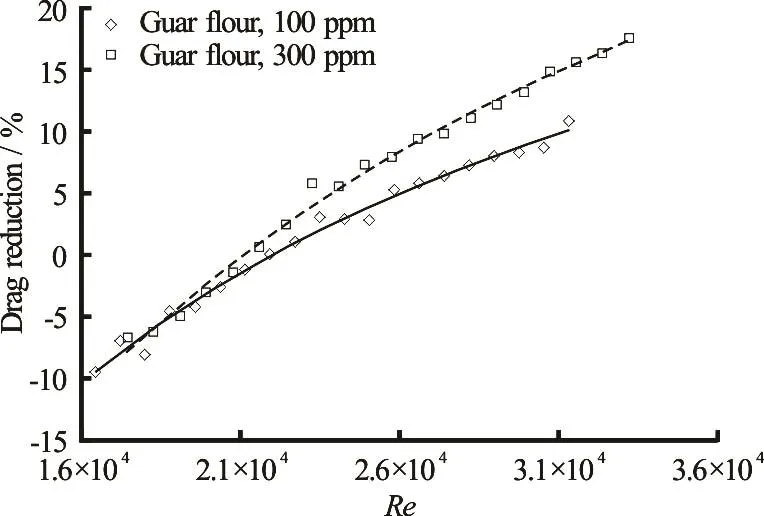
Fig.4 DR percentage vs. Re for guar flour

Fig.5 DR percentage vs. Re for Polyacrylonitrile fiber
3.2Part II: Fibers
3.2.1 Carbon fillers
The influence of carbon fillers (SFC-B10) (with concentrations of 300 ppm and 500 ppm) on pressure drop is shown in Fig.3 as a function of Reynolds number and compared with those from xanthan gum.It is interesting to see that carbon fillers produce no DR effect. In contrast, this type of rigid fibers leads to extra pressure drop in the system. The pressure drop increase was up to 5%. This effect can be attributed to their low length to diameter ratio and relatively high specific gravity and will be discussed in more details in Section 3.3. Carbon fillers are not able to modify the near-wall turbulence structure even at higher concentration of 500 ppm. Although the increase in pressure drop is slightly higher at low Re values, the slope of the trend line is very low. It can be seen also that results of both 300 ppm and 500 ppm are very close to each other.
3.2.2 Polyacrylonitrile fiber
The results corresponding to this type of fiber(PAC251) are given in Fig.5. Three different particle lengths namely 1.6 mm, 3 mm and 6 mm have been examined. It is seen from the figure that, the shortest fiber increases the pressure drop in the pipeline for the whole range of flow rates examined. Maximum increase of 5% in the pressure drop was observed for 300 ppm of 1.6 mm length fiber. The results for both 300 and 500 ppm concentrations are in the same range.This effect is due to low Stokes number of particles.By using 3 mm long fibers, pressure drop remains close to that of pure water but minor drag reduction effect was observed. Interestingly, 6 mm length fibers atc=500ppm showed drag reduction up to 3%.This part of the experiment proves that, in the case of rigid fibers, the ratio of fiber length to diameter plays the main role in DR. At low aspect ratios, particles cannot change the flow field structures. They can lead to a lower pressure drop only when their aspect ratio is sufficiently high.
It must be pointed out that, we should not expect high levels of drag reduction in dilute regimes of fiber-laden flows. This statement is supported by numerical studies of Zhao et al.[35]. They examined elongated ellipsoids with major and minor radii of 480 μm and 96 μm at volume fraction ofφ= 3.6×10-4andSt+=τp/τV=30. Drag reduction of less than 1% was observed in their simulations.
3.3Physical effect of additives
We are interested in the effect of additives on flow field based on the results given. In particular,finding the conditions that fibers decrease the pressure drop is important.
In DR by polymers the change of polymer structure from a coiled to a stretched one is an important factor. The strain rate and vorticity fields in the buffer layer make it possible that this stretching leads to a larger thickness of the buffer layer[11]. Therefore,higher effective viscosity in this region leads to the reduction of momentum flux to the wall more than viscous drag enhancement and consequently dissipative eddies are damped. This effect is also influenced by Reynolds number because this transition to stretched formation is triggered easier at higher Reynolds numbers. For xanthan gum the transition occurs at relatively low Reynolds numbers.
Now the reason behind the change in pressure drop by rigid fibers will be discussed. Turbulence intensity and pressure drop of particle-laden flows are influenced by particle shape, density, diameter (Stokes number) and volume fraction.
The particle response time for ellipsoid particles can be evaluated by[36]
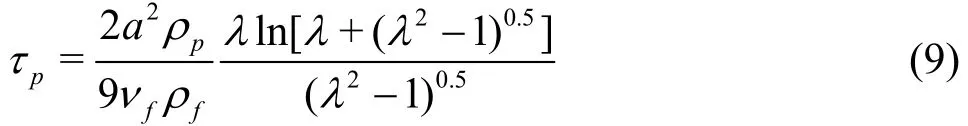
where and a are the aspect ratio and length of minor-axis of the particle, respectively.
For carbon fillers examined in this paper(SFC-B10, Section 3.2.1) particle size and density lead to very low Stokes number of particle based on friction velocity+0.04-0.13 St ≈ . These particles are referred to as “microparticles”[30]. Due to relatively small size of particles they can follow the streamlines which leads to higher flow turbulence.
In general, total change of stresses in the system can be understood by the streamwise momentum budget which can be expressed by three terms[26]

where is the total stress, τTis the turbulent Reynolds shear stress, τVis the viscous stress and τSis the stress induced by solid phase. In dilute regimes of carbon fillers, the increase of pressure drop can be justified by particle-induced stresses along with the increase of turbulence intensity of the fluid itself.The effect of particle-induced stresses on pressure drop enhancement was also reported in numerical studies of Ref.[26].
Polyacrylonitrile fibers' behavior depends strongly on particle size and aspect ratio. By increasing the particle length from lp=1.6 mm to 6 mm particle Stokes number ( S t+) increases (from 0.58 to 0.75).Consequently, particle effect on the flow is expected to change from “ghost” particles (for lp=1.6mm) to“critical” particles (for lp=6mm). Ghost particle does not influence the TKE. However, viscous stressesVτ and particle-induced stressesSτ lead to higher pressure drop in the system. By further increasing the particle length (and aspect ratio) critical regime is reached. In the scope of critical regime,TKE of the fluid phase is reduced. These two effects of reduction of fluid flow turbulent intensity and particle-induced stress, counteract each other at some point and further increase of particle Stokes number results in drag reduction for 6 mm long fibers.
Larger particleStokes numbers+( 1)St≥which can occur as a result of big particle selection(not present in this study) induce extra effect on turbulence intensity augmentation in dilute regime.Vortex shedding behind these particles gives rise to turbulence intensity even in the dilute regime.
Effect of volume fraction in this study can be explained by tendency of the system to move from a dilute to dense regime. Approaching dense regime means that particle can change the structure of streamwise vortices, weaken their strength, thus reducing turbulence intensity. It must be noted also that fibers are more efficient in systems with large enough pipes and less elbows so that high volume fraction without any worry on system blockage can be reached. Furthermore, fibers are more resistant,particularly at high Reynolds numbers, where polymers are subject to high scission rates. It would also be helpful to select particles of better elasticity.
4. Conclusions
The influence of polymers and fibers on pressure drop in a channel flow of rectangular cross section has been experimentally investigated. Xanthan gum, guar flour, carbon filler and polyacrylonitrile fibers have been considered as additive. Based on our observations, following conclusions can be drawn:
(1) A solution of 200 ppm xanthan gum revealed a noticeable DR of 22% at R e = 33000. However,this DRA loses its efficiency rapidly. Guar flour is another polymer examined in this experiment. At low Reynolds numbers, guar flour increased pressure drop for both 100 ppm and 300 ppm solutions. However, a drag reduction of up to 18% can be achieved with 300 ppm of guar flour.
(2) Carbon fillers at 300 ppm and 500 ppm were tested as well. In both concentrations, an increase in pressure drop was seen, which is justified by their low ratio of length to diameter and low Stokes number.
(3) Polyacrylonitrile fiber is another additive which is examined and introduced as a potential DRA with good rigidity. It demonstrates up to 3% drag reduction at high particle lengths with only 500 ppm concentration. Therefore, rigid particles decrease the pressure drop in the channel flow only when they have sufficiently high aspect ratios. However, due to their better resistance, mechanical degradation does not occur. This fiber is expected to yield more drag reduction if used in higher concentrations. In this study, due to small diameter of piping we tested concentrations up to 500 ppm.
Based on the results shown, for future studies with rigid particles it would be helpful to use particles with following characteristics:
(1) It is recommended to use particles of high aspect ratios (>100) to get more DR. For the same aspect ratio, moderate particle Stokes numbers are preferred. For Stokes numbers in the upper range of criteria mentioned, lower particle aspect ratios can be used. However, it must be noted that very large particles (with higher Stokes numbers) experience wake shedding, which increases turbulence and pressure drop consequently. Then, very large volume fractions and Reynolds numbers are probably required to get small levels of DR.
(2) The next point is the proper selection of solid-phase volume fraction. Higher volume fractions of moderate Stokes number particles usually lead to more attenuation of turbulence.
(3) Fibers can be preferably used as DRA in systems of relatively large size with few elbows to make high solid-phase volume fractions possible without any pipe blockage.
(4) Better elasticity of particle is useful to reduce the pressure drop more but it is not a necessary parameter.
For future studies, using higher volume fractions of rigid particles and high Stokes number particles are recommended.
Acknowledgements
The financial support of the German research foundation (DFG) within the graduate college for micro-macro-interactions in structured media and particle systems (GRK 1554) is gratefully acknowledged.
[1] Shao X., Lin J., Wu T. et al. Experimental research on drag reduction by polymer additives in a turbulent pipe flow [J]. Canadian Journal of Chemical Engineering,2002, 80(2): 293-298.
[2] Edomwonyi-Otu L. C., Chinaud M., Angeli P. Effect of drag reducing polymer on horizontal liquid–liquid flows[J]. Experimental Thermal and Fluid Science, 2015, 64:164-174.
[3] Steele A., Bayer I. S., Loth E. Pipe flow drag reduction effects from carbon nanotube additives [J]. Carbon, 2014,77(2): 1183-1186.
[4] Shao X., Wu T., Yu Z. Fully resolved numerical simulation of particle-laden turbulent flow in a horizontal channel at a low Reynolds number [J]. Journal of Fluid Mechanics, 2012, 693: 319-344.
[5] Uhlmann M. Interface-resolved direct numerical simulation of vertical particulate channel flow in the turbulent regime [J]. Physics of Fluids, 2008, 20(5): 53305.
[6] Gyr A., Bewersdorff H.-W. Drag reduction of turbulent flows by additives [M]. Dordrecht, The Netherlands:Kluwer Academic, 1995.
[7] Toms B. A. Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers [C]. First International Congress on Rheology.Scheveningen, The Netherlands, 1948, 135-141.
[8] Warholic M. D., Massah H., Hanratty T. J. Influence of drag-reducing polymerson turbulence:Effectsof Reynolds number, concentration and mixing [J]. Experiments in Fluids, 1999, 27(5): 461-472.
[9] Ptasinski P. K., Nieuwstadt F. T. M., Van Den Brule B. et al. Experiments in turbulent pipe flow with polymer additives at maximum drag reduction [J]. Flow, Turbulence and Combustion, 2001, 66(2): 159-182.
[10] Mowla D., Naderi A. Experimental study of drag reduction by a polymeric additive in slug two-phase flow of crude oil and air in horizontal pipes [J]. Chemical Engineering Science, 2006, 61(5): 1549-1554.
[11] White C. M., Mungal M. G. Mechanics and prediction of turbulent drag reduction with polymer additives [J].Annual Review of Fluid Mechanics, 2008, 40(1): 235-256.
[12] Lumley J. L. Drag reduction by additives [J]. Annual Review of Fluid Mechanics, 1969, 1(1): 367-384.
[13] Ryskin G. Turbulent drag reduction by polymers: A quantitative theory [J]. Physical Review Letters, 1987,59(18): 2059.
[14] Gillissen J. J. J. Polymer flexibility and turbulent drag reduction [J]. Physical Review E Statistical Nonlinear and Soft Matter Physics, 2008, 78(4): 046311.
[15] Tabor M., De Gennes P. G. A cascade theory of drag reduction [J]. Europhysics Letters, 1986, 2(7): 519-522.
[16] Japper-Jaafar A., Escudier M. P., Poole R. J. Turbulent pipe flow of a drag-reducing rigid “rod-like” [J]. Journal of Non-Newtonian Fluid Mechanics, 2009, 161(1-3):86-93.
[17] Cai S. P., Higuchi Y. Drag-reduction behavior of an unusual nonionic surfactant in a circular pipe turbulent flow[J]. Journal of Hydrodynamics, 2014, 26(3): 400-405.
[18] Elbing B. R., Winkel E. S., Lay K. A. et al. Bubble-induced skin-friction drag reduction and the abrupt transition to air-layer drag reduction [J].Journal of Fluid Mechanics, 2008, 612: 201-236.
[19] Pouranfard A. R., Mowla D., Esmaeilzadeh F. An experimental study of drag reduction by nanofluids through horizontal pipe turbulent flow of a Newtonian liquid [J].Journal of Industrial and Engineering Chemistry, 2014,20(2): 633-637.
[20] Radin I.,. Zakin J. L., Patterson G. K. Drag reduction in solid-fluid systems [J]. AIChE Journal, 1975, 21(2):358-371.
[21] You Z. J., Lin J. Z., Shao X. M. et al. Stability and drag reduction in transient channel flow of fibre suspension [J].Chinese Journal of Chemical Engineering, 2004, 12(3):319-323.
[22] Ko G. H., Heo K., Lee K. et al. An experimental study on the pressure drop of nanofluids containing carbon nanotubes in a horizontal tube [J]. International Journal of Heat and Mass Transfer, 2007, 50(23-24): 4749-4753.
[23] Liu Z. H., Liao L. Forced convective flow and heat transfer characteristics of aqueous drag-reducing fluid with carbon nanotubes added [J]. International Journal of Thermal Sciences, 2010, 49(12): 2331-2338.
[24] Lin J. Z., Xia Y., Ku X. K. Flow and heat transfer characteristics of nanofluids containing rod-like particles in a turbulent pipe flow [J]. International Journal of Heat and Mass Transfer, 2016, 93: 57-66.
[25] Zhao F., van Wachem B. G. M. Direct numerical simulation of ellipsoidal particles in turbulent channel flow [J].Acta Mechanica, 2013, 224(10): 2331-2358.
[26] Picano F., Breugem W.-P., Brandt L. Turbulent channel flow of dense suspensions of neutrally buoyant spheres [J].Journal of Fluid Mechanics, 2015, 764: 463-487.
[27] Lin J. Z., Xia Y., Ku X. K. Pressure drop and heat transfer of nanofluid in turbulent pipe flow considering particle coagulation and breakage [J]. Journal of Heat Transfer,2014 , 136(11): 111701.
[28] von Kármán T. Mechanische Ähnlichkeit und turbulenz[C]. Proceedings of the 3rd International Congress for Applied Mechanics. Stockholm, Sweden, 1930, 85-105.
[29] Virk P. S. Drag reduction fundamentals [J]. AIChE Journal, 1975, 21(4): 625-656.
[30] Elghobashi S. An updated classification map of particleladen turbulent flows [C]. IUTAM Symposium on Computational Approaches to Multiphase Flow. Berlin,Germany: Springer, 2006, 3-10.
[31] Elghobashi S. On predicting particle-laden turbulent flows[J]. Applied Scientific Research, 1994, 52(4): 309-329.
[32] Fornari W., Formenti A., Picano F. et al. The effect of particle density in turbulent channel flow laden with finite size particles in semi-dilute conditions [J]. Physics of Fluids, 2016, 28(3): 033301.
[33] Garcıa-Ochoa F., Santos V. E., Casas J. A. et al. Xanthan gum: Production, recovery, and properties [J]. Biotechnology Advances, 2000, 18(7): 549-579.
[34] Soares E. J., Sandoval G. A. B., Silveira L. et al. Loss of efficiency of polymeric drag reducers induced by high Reynolds number flows in tubes with imposed pressure [J].Physics of Fluids, 2015, 27(12): 125105.
[35] Zhao F., George W. K., van Wachem B. G. M. Four-way coupled simulations of small particles in turbulent channel flow: The effects of particle shape and Stokes number [J].Physics of Fluids, 2015, 27(8): 083301.
[36] Shapiro M., Goldenberg M. Deposition of glass fiber particles from turbulent air flow in a pipe [J]. Journal of Aerosol Science, 1993, 24(1): 65-87.
March 16, 2017, Revised April 10, 2017)
* Biography: Amir Eshghinejadfard (1983-), Male,Ph. D. Candidate
杂志排行
水动力学研究与进展 B辑的其它文章
- On the clean numerical simulation (CNS) of chaotic dynamic systems *
- BEM for wave interaction with structures and low storage accelerated methods for large scale computation *
- Flow-pipe-soil coupling mechanisms and predictions for submarine pipeline instability *
- Simulation of flows with moving contact lines on a dual-resolution Cartesian grid using a diffuse-interface immersed-boundary method *
- On the hydrodynamics of hydraulic machinery and flow control *
- A 3-D SPH model for simulating water flooding of a damaged floating structure *
